Capítulo 11 Variables Dependientes Categóricas
Vista Previa del Capítulo. Un modelo con una variable dependiente categórica permite predecir si una observación pertenece a un grupo o categoría distinta. Las variables binarias representan un caso especial importante; pueden indicar si un evento de interés ha ocurrido o no. En aplicaciones actuariales y financieras, el evento puede ser si ocurre un siniestro, si una persona compra un seguro, si una persona se jubila o si una empresa se vuelve insolvente. Este capítulo introduce los modelos de regresión logística y probit para variables dependientes binarias. Las variables categóricas también pueden representar más de dos grupos, conocidos como resultados multicategoría. Las variables multicategoría pueden estar desordenadas o ordenadas, dependiendo de si tiene sentido clasificar los resultados de la variable. Para los resultados esordenados, conocidos como variables nominales, el capítulo introduce los modelos de logits generalizados y logit multinomial. Para los resultados ordenados, conocidos como variables ordinales, el capítulo introduce los modelos de logit acumulativo y probit.
11.1 Variables Dependientes Binarias
Ya hemos introducido las variables binarias como un tipo especial de variable discreta que puede utilizarse para indicar si un sujeto tiene una característica de interés, como el sexo de una persona o la propiedad de una empresa de seguros cautiva por parte de una firma. Las variables binarias también describen si ha ocurrido o no un evento de interés, como un accidente. Un modelo con una variable dependiente binaria permite predecir si ha ocurrido un evento o si un sujeto tiene una característica de interés.
Ejemplo: Gastos MEPS. La Sección 11.4 describirá una extensa base de datos de la Encuesta del Panel de Gastos Médicos (MEPS, por sus siglas en inglés) sobre la utilización y los gastos de hospitalización. Para estos datos, consideraremos \[ y_i = \left\{ \begin{array}{ll} 1 & \text{la i-ésima persona fue hospitalizada durante el período de la muestra} \\ 0 & \text{de lo contrario} \end{array} \right. . \] Hay \(n=2,000\) personas en esta muestra, distribuidas de la siguiente manera:
| Hombres | Mujeres | ||
|---|---|---|---|
| No hospitalizado | \(y=0\) | 902 (95.3%) | 941 (89.3%) |
| Hospitalizado | \(y=1\) | 44 (4.7%) | 113 (10.7%) |
| Total | 946 | 1,054 |
Código R para Generar la Tabla 11.1
La Tabla 11.1 sugiere que el sexo tiene una influencia importante sobre si una persona se hospitaliza.
Al igual que con las técnicas de regresión lineal introducidas en capítulos anteriores, estamos interesados en usar las características de una persona, como su edad, sexo, educación, ingresos y estado de salud previo, para ayudar a explicar la variable dependiente \(y\). A diferencia de los capítulos anteriores, ahora la variable dependiente es discreta y no sigue una distribución normal, ni siquiera de manera aproximada. En circunstancias limitadas, la regresión lineal puede usarse con variables dependientes binarias; esta aplicación se conoce como un modelo de probabilidad lineal.
Modelos de Probabilidad Lineal
Para introducir algunas de las complejidades que se encuentran con variables dependientes binarias, denotemos la probabilidad de que la respuesta sea igual a 1 como \(\pi_i= \mathrm{Pr}(y_i=1)\). Una variable aleatoria binaria tiene una distribución de Bernoulli. Por lo tanto, podemos interpretar la respuesta media como la probabilidad de que la respuesta sea uno, es decir, \(\mathrm{E~}y_i\) \(=0\times \mathrm{Pr}(y_i=0) + 1 \times \mathrm{Pr}(y_i=1)\) \(= \pi_i\). Además, la varianza está relacionada con la media a través de la expresión \(\mathrm{Var}~y_i = \pi_i(1-\pi_i)\).
Comenzamos considerando un modelo lineal de la forma \[ y_i = \mathbf{x}_i^{\mathbf{\prime}} \boldsymbol \beta + \varepsilon_i, \]
conocido como modelo de probabilidad lineal. Asumiendo \(\mathrm{E~}\varepsilon_i=0\), tenemos que \(\mathrm{E~}y_i=\mathbf{x}_i^{\mathbf{\prime }} \boldsymbol \beta =\pi_i\). Dado que \(y_i\) tiene una distribución de Bernoulli, \(\mathrm{Var}~y_i=\mathbf{x}_i^{\mathbf{\prime}} \boldsymbol \beta(1-\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta)\). Los modelos de probabilidad lineal se utilizan debido a la facilidad de interpretación de los parámetros. Para conjuntos de datos grandes, la simplicidad computacional de los estimadores de mínimos cuadrados ordinarios es atractiva en comparación con algunos modelos no lineales más complejos que se introducen más adelante en este capítulo. Como se describió en el Capítulo 3, los estimadores de mínimos cuadrados ordinarios para \(\boldsymbol \beta\) tienen propiedades deseables. Es sencillo comprobar que los estimadores son consistentes y asintóticamente normales bajo condiciones moderadas sobre las variables explicativas {\(\mathbf{x}_i\)}. Sin embargo, los modelos de probabilidad lineal tienen varios inconvenientes que son graves en muchas aplicaciones.
Desventajas del Modelo de Probabilidad Lineal
Los valores ajustados pueden ser inadecuados. La respuesta esperada es una probabilidad y, por lo tanto, debe variar entre 0 y 1. Sin embargo, la combinación lineal, \(\mathbf{x}_i^{\mathbf{\prime}} \boldsymbol \beta\), puede variar entre infinito negativo y positivo. Esta desproporción implica, por ejemplo, que los valores ajustados pueden ser poco razonables.
Heterocedasticidad. Los modelos lineales suponen homocedasticidad (varianza constante), pero la varianza de la respuesta depende de la media, que varía entre las observaciones. El problema de la variabilidad cambiante se conoce como heterocedasticidad.
El análisis de los residuos no tiene sentido. La respuesta debe ser 0 o 1, aunque los modelos de regresión generalmente consideran la distribución del término de error como continua. Esta desproporción implica, por ejemplo, que el análisis usual de los residuos en los modelos de regresión no tiene sentido.
Para manejar el problema de la heterocedasticidad, es posible un procedimiento de mínimos cuadrados ponderados (en dos etapas). En la primera etapa, se usan mínimos cuadrados ordinarios para calcular estimaciones de \(\boldsymbol \beta\). Con esta estimación, se puede calcular una varianza estimada para cada sujeto utilizando la relación \(\mathrm{Var}~y_i=\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta (1-\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta)\). En la segunda etapa, se realiza un ajuste de mínimos cuadrados ponderados utilizando el inverso de las varianzas estimadas como ponderaciones para obtener nuevas estimaciones de \(\boldsymbol \beta\). Es posible iterar este procedimiento, aunque estudios han demostrado que tiene pocas ventajas hacerlo (ver Carroll y Ruppert, 1988). Alternativamente, se pueden usar estimadores de mínimos cuadrados ordinarios de \(\boldsymbol \beta\) con errores estándar robustos a la heterocedasticidad (ver Sección 5.7.2).
11.2 Modelos de Regresión Logística y Probit
11.2.1 Uso de Funciones No Lineales de Variables Explicativas
Para evitar las desventajas de los modelos de probabilidad lineal, consideramos modelos alternativos en los que expresamos la expectativa de la respuesta como una función de las variables explicativas, \(\pi_i=\mathrm{\pi }(\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta)\) \(=\Pr (y_i=1|\mathbf{x}_i)\). Nos centramos en dos casos especiales de la función \(\mathrm{\pi }(\cdot)\):
\(\mathrm{\pi }(z)=\frac{1}{1+\exp (-z)}=\frac{e^{z}}{1+e^{z}}\), el caso logit, y
\(\mathrm{\pi }(z)=\mathrm{\Phi }(z)\), el caso probit.
Aquí, \(\mathrm{\Phi }(\cdot)\) es la función de distribución normal estándar. La elección de la función identidad (un tipo especial de función lineal), \(\mathrm{\pi }(z)=z\), da lugar al modelo de probabilidad lineal. En cambio, \(\mathrm{\pi}\) es no lineal tanto en el caso logit como en el probit. Estas dos funciones son similares en el sentido de que están casi linealmente relacionadas en el intervalo \(0.1 \le p \le 0.9\). Así que, en gran medida, la elección de la función depende de las preferencias del analista. La Figura 11.1 compara las funciones logit y probit, mostrando que será difícil distinguir entre las dos especificaciones en la mayoría de los conjuntos de datos.
La inversa de la función, \(\mathrm{\pi }^{-1}\), especifica la forma de la probabilidad que es lineal en las variables explicativas, es decir, \(\mathrm{\pi }^{-1}(\pi_i)= \mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta\). En el Capítulo 13, nos referimos a esta inversa como la función de enlace.
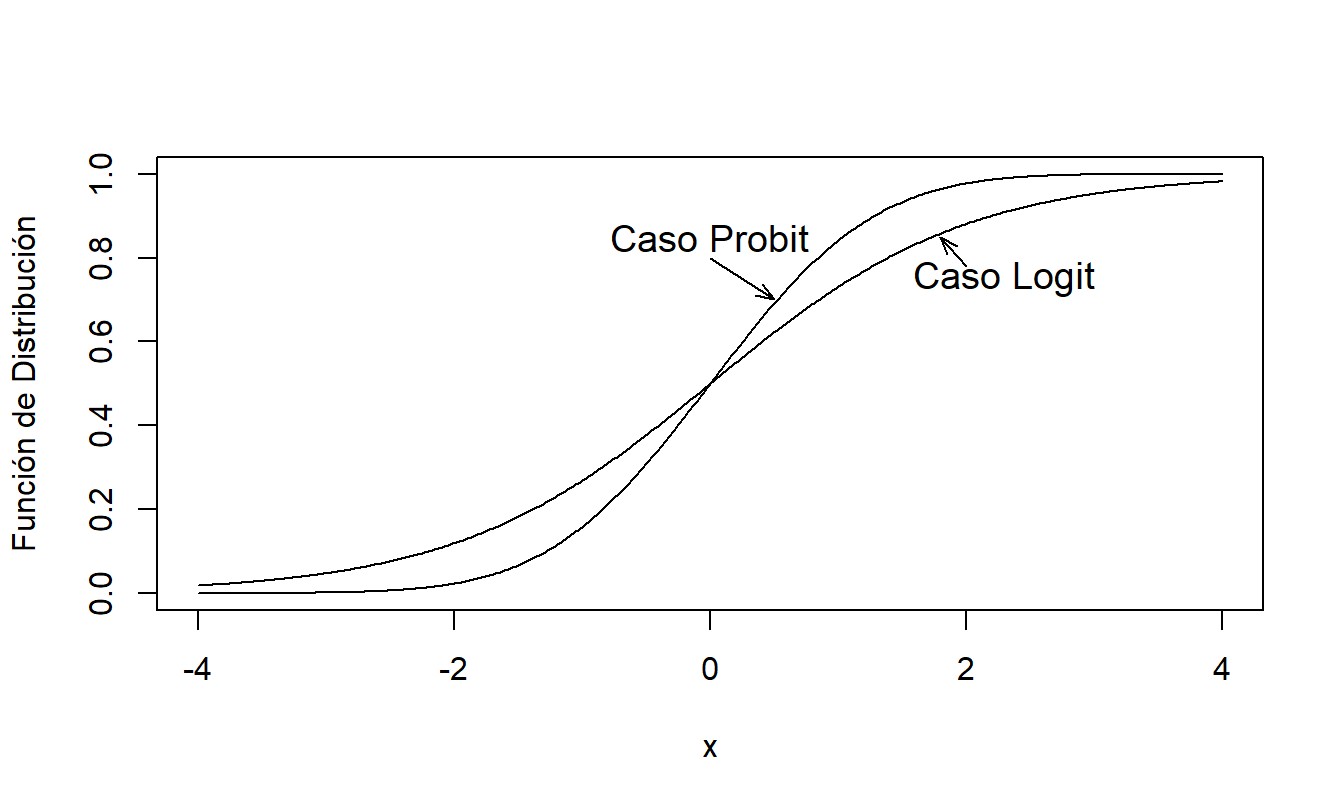
Figura 11.1: Comparación de la Distribución Logit y Probit (Normal Estándar)
Ejemplo: Puntuación de Crédito. Los bancos, las agencias de crédito y otras instituciones financieras desarrollan “puntuaciones de crédito” para individuos que se utilizan para predecir la probabilidad de que el prestatario reembolse sus deudas actuales y futuras. Se dice que las personas que no cumplen con los plazos de pago estipulados en un acuerdo de préstamo están en “incumplimiento”. Una puntuación de crédito es entonces una probabilidad predicha de estar en incumplimiento, utilizando la información de la solicitud de crédito como variables explicativas para desarrollar la puntuación. La elección de las variables explicativas depende del propósito de la solicitud; la puntuación de crédito se usa tanto para emitir tarjetas de crédito para pequeñas compras de consumo como para solicitudes de hipotecas de casas multimillonarias. En la Tabla 11.2, Hand y Henley (1997) proporcionan una lista de características típicas que se utilizan en la puntuación de crédito.
Tabla 11.2. Características Utilizadas en Algunos Procedimientos de Puntuación de Crédito
\[ \small{ \begin{array}{ll} \hline \textbf{Características} & \textbf{Valores Potenciales} \\ \hline \text{Tiempo en la dirección actual} & \text{0-1, 1-2, 3-4, 5+ años}\\ \text{Estado de la vivienda} & \text{Propietario, inquilino, otro }\\ \text{Código postal} & \text{Rango A, B, C, D, E} \\ \text{Teléfono} & \text{Sí, no} \\ \text{Ingresos anuales del solicitante} & \text{£ (0-10000),} \text{£ (10,000-20,000)} \text{£ (20,000+)} \\ \text{Tarjeta de crédito} & \text{Sí, no} \\ \text{Tipo de cuenta bancaria} & \text{Corriente y/o ahorro, ninguna} \\ \text{Edad }& \text{18-25, 26-40, 41-55, 55+ años} \\ \text{Juicios del Tribunal del Condado} & \text{Número} \\ \text{Tipo de ocupación} & \text{Codificado} \\ \text{Propósito del préstamo} & \text{Codificado} \\ \text{Estado civil} & \text{Casado, divorciado, soltero, viudo, otro} \\ \text{Tiempo con el banco} & \text{Años} \\ \text{Tiempo con el empleador} & \text{Años }\\ \hline \textit{Fuente}: \text{Hand y Henley (1997)} \\ \end{array} } \]
Con la información de la solicitud de crédito y la experiencia de incumplimiento, se puede utilizar un modelo de regresión logística para ajustar la probabilidad de incumplimiento con puntuaciones de crédito derivadas de los valores ajustados. Wiginton (1980) proporciona una de las primeras aplicaciones de la regresión logística a la puntuación de crédito de consumidores. En ese momento, otros métodos estadísticos conocidos como análisis discriminante estaban a la vanguardia de las metodologías de puntuación cuantitativa. En su artículo de revisión, Hand y Henley (1997) discuten otros competidores de la regresión logística, incluidos los sistemas de aprendizaje automático y las redes neuronales. Como señalan Hand y Henley, no existe un “mejor” método de manera uniforme. Las técnicas de regresión son importantes por sí mismas debido a su uso generalizado y porque pueden proporcionar una plataforma para aprender sobre métodos más nuevos.
Las puntuaciones de crédito estiman la probabilidad de incumplimiento en préstamos, pero los emisores de crédito también están interesados en la cantidad y el momento del pago de la deuda. Por ejemplo, un “buen” riesgo puede pagar un saldo de crédito tan rápidamente que el prestamista obtiene pocas ganancias. Además, un mal riesgo hipotecario puede incumplir un préstamo tan tarde en el contrato que el prestamista ya ha ganado suficiente ganancia. Véase Gourieroux y Jasiak (2007) para una discusión amplia sobre cómo el modelado de crédito puede usarse para evaluar el riesgo y la rentabilidad de los préstamos.
11.2.2 Interpretación del Umbral
Tanto el caso logit como el probit se pueden interpretar de la siguiente manera. Supongamos que existe un modelo lineal subyacente, \(y_i^{\ast} = \mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta + \varepsilon_i^{\ast}\). Aquí, no observamos la respuesta \(y_i^{\ast}\), pero la interpretamos como la “propensión” a poseer una característica. Por ejemplo, podríamos pensar en la fortaleza financiera de una empresa de seguros como una medida de su propensión a volverse insolvente (incapaz de cumplir con sus obligaciones financieras). Bajo la interpretación del umbral, no observamos la propensión, pero sí observamos cuando la propensión cruza un umbral. Es habitual asumir que este umbral es 0, por simplicidad. Así, observamos \[ y_i=\left\{ \begin{array}{ll} 0 & y_i^{\ast} \le 0 \\ 1 & y_i^{\ast}>0 \end{array} \right. . \] Para ver cómo se deriva el caso logit a partir del modelo del umbral, supongamos una función de distribución logística para las perturbaciones, de modo que \[ \mathrm{\Pr }(\varepsilon_i^{\ast} \le a)=\frac{1}{1+\exp (-a)}. \] Al igual que la distribución normal, se puede verificar calculando la densidad que la distribución logística es simétrica alrededor de cero. Así, \(-\varepsilon_i^{\ast}\) tiene la misma distribución que \(\varepsilon_i^{\ast}\) y entonces \[ \pi_i =\Pr (y_i=1|\mathbf{x}_i)=\mathrm{\Pr }(y_i^{\ast}>0) =\mathrm{ \Pr }(\varepsilon_i^{\ast} \le \mathbf{x}_i^{\mathbf{\prime}}\mathbf{\beta }) =\frac{1}{1+\exp (-\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta)} =\mathrm{\pi }(\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta). \] Esto establece la interpretación del umbral para el caso logit. El desarrollo para el caso probit es similar y se omite.
11.2.3 Interpretación de Utilidad Aleatoria
Tanto el caso logit como el probit también se justifican apelando a la siguiente interpretación de “utilidad aleatoria” del modelo. En algunas aplicaciones económicas, los individuos seleccionan una de dos opciones. Aquí, las preferencias entre opciones están indexadas por una función de utilidad no observada; los individuos seleccionan la opción que les brinda mayor utilidad.
Para el sujeto \(i\), utilizamos la notación \(u_i\) para esta función de utilidad. Modelamos la utilidad (\(U\)) como una función de un valor subyacente (\(V\)) más un ruido aleatorio (\(\varepsilon\)), es decir, \(U_{ij}=u_i(V_{ij}+\varepsilon_{ij})\), donde \(j\) puede ser 1 o 2, correspondiente a la elección. Para ilustrar, asumimos que el individuo elige la categoría correspondiente a \(j=1\) si \(U_{i1}>U_{i2}\) y denotamos esta elección como \(y_i=1\). Asumiendo que \(u_i\) es una función estrictamente creciente, tenemos \[\begin{eqnarray*} \Pr (y_i &=&1)=\mathrm{\Pr }(U_{i2}<U_{i1})=\mathrm{\Pr }\left( u_i(V_{i2}+\varepsilon_{i2})<u_i(V_{i1}+\varepsilon_{i1})\right) \\ &=&\mathrm{\Pr }(\varepsilon_{i2}-\varepsilon_{i1}<V_{i1}-V_{i2}). \end{eqnarray*}\]
Para parametrizar el problema, asumimos que el valor \(V\) es una combinación lineal desconocida de las variables explicativas. Específicamente, tomamos \(V_{i2}=0\) y \(V_{i1}=\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta\). Podemos asumir que la diferencia en los errores, \(\varepsilon_{i2}-\varepsilon_{i1}\), sigue una distribución normal o logística, correspondiente a los casos probit y logit, respectivamente. La distribución logística se cumple si asumimos que los errores tienen una distribución de valor extremo, o Gumbel (ver, por ejemplo, Amemiya, 1985).
11.2.4 Regresión Logística
Una ventaja del caso logit es que permite expresiones en forma cerrada, a diferencia de la función de distribución normal. Regresión logística es otra frase utilizada para describir el caso logit.
Usando \(p=\mathrm{\pi }(z)= \left( 1+ \mathrm{e}^{-z}\right)^{-1}\), la inversa de \(\mathrm{\pi }\) se calcula como \(z=\mathrm{\pi }^{-1}(p)=\ln(p/(1-p))\). Para simplificar presentaciones futuras, definimos \[ \mathrm{logit}(p)=\ln \left( \frac{p}{1-p}\right) \] como la función logit. Con un modelo de regresión logística, representamos la combinación lineal de variables explicativas como el logit de la probabilidad de éxito, es decir, \(\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta=\mathrm{logit}(\pi_i)\).
Interpretación de los Odds
Cuando la respuesta \(y\) es binaria, conocer solo \(p=\Pr(y=1)\) resume toda la distribución. En algunas aplicaciones, una simple transformación de \(p\) tiene una interpretación importante. El ejemplo más común de esto son los odds, dados por \(p/(1-p)\). Por ejemplo, supongamos que \(y\) indica si un caballo gana una carrera y \(p\) es la probabilidad de que el caballo gane. Si \(p=0.25\), entonces los odds de que el caballo gane son \(0.25/(1.00-0.25)=0.3333\). Podríamos decir que los odds de ganar son 0.3333 a 1, o de uno a tres. De manera equivalente, decimos que la probabilidad de no ganar es \(1-p=0.75\), de modo que los odds de que el caballo no gane son \(0.75/(1-0.75)=3\) y los odds en contra del caballo son tres a uno.
Los odds tienen una interpretación útil desde el punto de vista de las apuestas. Supongamos que estamos jugando un juego justo y que hacemos una apuesta de 1 con odds de uno a tres. Si el caballo gana, entonces recuperamos nuestro 1 más una ganancia de 3. Si el caballo pierde, perdemos nuestra apuesta de 1. Es un juego justo en el sentido de que el valor esperado del juego es cero porque ganamos 3 con probabilidad \(p=0.25\) y perdemos 1 con probabilidad \(1-p=0.75\). Desde el punto de vista económico, los odds proporcionan los números importantes (apuesta de 1 y ganancia de 3), no las probabilidades. Por supuesto, si conocemos \(p\), siempre podemos calcular los odds. Del mismo modo, si conocemos los odds, siempre podemos calcular la probabilidad \(p\).
El logit es la función logarítmica de los odds, también conocida como log-odds.
Interpretación de la Razón de Momios
Para interpretar los coeficientes de regresión en el modelo de regresión logística, \(\boldsymbol \beta=(\beta_0,\ldots ,\beta_{k})^{\prime}\), comenzamos asumiendo que la \(j\)-ésima variable explicativa, \(x_{ij}\), es 0 o 1. Entonces, con la notación \(\mathbf{x}_i=(x_{i0},...,x_{ij},\ldots ,x_{ik})^{\prime}\), podemos interpretar
\[\begin{eqnarray*} \beta_j &=&(x_{i0},...,1,\ldots ,x_{ik})^{\prime}\boldsymbol \beta -(x_{i0},...,0,\ldots ,x_{ik})^{\prime}\boldsymbol \beta \\ &=&\ln \left( \frac{\Pr (y_i=1|x_{ij}=1)}{1-\Pr (y_i=1|x_{ij}=1)}\right) -\ln \left( \frac{\Pr (y_i=1|x_{ij}=0)}{1-\Pr (y_i=1|x_{ij}=0)}\right) \end{eqnarray*}\]
Así,
\[ e^{\beta_j}=\frac{\Pr (y_i=1|x_{ij}=1)/\left( 1-\Pr (y_i=1|x_{ij}=1)\right) }{\Pr (y_i=1|x_{ij}=0)/\left( 1-\Pr (y_i=1|x_{ij}=0)\right) }. \] Esto muestra que \(e^{\beta_j}\) puede expresarse como la razón de dos momios, conocida como la razón de momios. Es decir, el numerador de esta expresión es el momio cuando \(x_{ij}=1\), mientras que el denominador es el momio cuando \(x_{ij}=0\). Así, podemos decir que el momio cuando \(x_{ij}=1\) es \(\exp (\beta_j)\) veces mayor que el momio cuando \(x_{ij}=0\). Para ilustrar, supongamos que \(\beta_j=0.693\), de modo que \(\exp (\beta _j)=2\). A partir de esto, decimos que los momios (para \(y=1\)) son el doble para \(x_{ij}=1\) que para \(x_{ij}=0\).
De manera similar, suponiendo que la \(j\)-ésima variable explicativa es continua (diferenciable), tenemos \[\begin{eqnarray} \beta_j &=&\frac{\partial }{\partial x_{ij}}\mathbf{x}_i^{\prime} \boldsymbol \beta =\frac{\partial }{\partial x_{ij}}\ln \left( \frac{\Pr (y_i=1|x_{ij})}{1-\Pr (y_i=1|x_{ij})}\right) \nonumber \\ &=&\frac{\frac{\partial }{\partial x_{ij}}\Pr (y_i=1|x_{ij})/\left( 1-\Pr (y_i=1|x_{ij})\right) }{\Pr (y_i=1|x_{ij})/\left( 1-\Pr (y_i=1|x_{ij})\right) }. \tag{11.1} \end{eqnarray}\] Así, podemos interpretar \(\beta_j\) como el cambio proporcional en la razón de momios, conocido como elasticidad en economía.
Ejemplo: Gastos MEPS - Continuación. La Tabla 11.1 muestra que el porcentaje de mujeres que fueron hospitalizadas es del \(10.7\%\); alternativamente, el momio de que una mujer sea hospitalizada es \(0.107/(1-0.107)=0.120\). Para los hombres, el porcentaje es del \(4.7\%\), de modo que el momio es \(0.0493\). La razón de momios es \(0.120/0.0493=2.434\); las mujeres tienen más del doble de probabilidad de ser hospitalizadas que los hombres.
A partir de un ajuste de regresión logística (descrito en la Sección 11.4), el coeficiente asociado al sexo es \(0.733\). Con base en este modelo, decimos que las mujeres tienen \(\exp (0.733)=2.081\) veces más probabilidad que los hombres de ser hospitalizadas. La estimación de regresión de la razón de momios controla por variables adicionales (como edad y educación) en comparación con el cálculo básico basado en frecuencias crudas.
11.3 Inferencia para Modelos de Regresión Logística y Probit
11.3.1 Estimación de Parámetros
El método habitual de estimación para modelos logísticos y probit es el máxima verosimilitud, descrito con más detalle en la Sección 11.9. Para proporcionar una intuición, describimos las ideas en el contexto de los modelos de regresión con variables dependientes binarias.
La verosimilitud es el valor observado de la función de probabilidad. Para una sola observación, la verosimilitud es \[ \left\{ \begin{array}{ll} 1-\pi_i & \mathrm{si}\ y_i=0 \\ \pi_i & \mathrm{si}\ y_i=1 \end{array} \right. . \] El objetivo de la estimación de máxima verosimilitud es encontrar los valores de los parámetros que producen la mayor verosimilitud. Encontrar el máximo de la función logarítmica produce la misma solución que encontrar el máximo de la función correspondiente. Debido a que generalmente es más sencillo computacionalmente, consideramos la verosimilitud logarítmica (o log-verosimilitud), escrita como \[\begin{equation} \left\{ \begin{array}{ll} \ln \left( 1-\pi_i\right) & \mathrm{si}\ y_i=0 \\ \ln \pi_i & \mathrm{si}\ y_i=1 \end{array} \right. . \tag{11.2} \end{equation}\] De manera más compacta, la log-verosimilitud de una sola observación es \[ y_i\ln \mathrm{\pi }(\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta) + (1-y_i) \ln \left( 1-\mathrm{\pi }(\mathbf{x}_i^{\mathbf{\prime}} \boldsymbol \beta)\right) , \] donde \(\pi_i=\mathrm{\pi }(\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta)\). Asumiendo independencia entre las observaciones, la verosimilitud del conjunto de datos es un producto de las verosimilitudes de cada observación. Tomando logaritmos, la log-verosimilitud del conjunto de datos es la suma de las log-verosimilitudes de cada observación.
La log-verosimilitud del conjunto de datos es \[\begin{equation} L(\boldsymbol \beta)=\sum\limits_{i=1}^{n}\left\{ y_i\ln \mathrm{\pi }( \mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta) + (1-y_i) \ln \left( 1- \mathrm{\pi }(\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta)\right) \right\} . \tag{11.3} \end{equation}\] La log-verosimilitud se considera como una función de los parámetros, con los datos fijos. En contraste, la función de probabilidad conjunta se considera como una función de los datos realizados, con los parámetros fijos.
El método de máxima verosimilitud consiste en encontrar los valores de \(\boldsymbol \beta\) que maximizan la log-verosimilitud. El método habitual para encontrar el máximo es tomar las derivadas parciales con respecto a los parámetros de interés y encontrar las raíces de las ecuaciones resultantes. En este caso, al tomar las derivadas parciales con respecto a \(\boldsymbol \beta\) se obtienen las ecuaciones de puntaje:
\[\begin{equation} \frac{\partial }{\partial \boldsymbol \beta}L(\boldsymbol \beta )=\sum\limits_{i=1}^{n}\mathbf{x}_i\left( y_i-\mathrm{\pi }(\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta)\right) \frac{\mathrm{\pi }^{\prime}( \mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta)}{\mathrm{\pi }(\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta)(1-\mathrm{\pi }(\mathbf{x}_i^{ \mathbf{\prime}}\boldsymbol \beta))}=\mathbf{0}, \tag{11.4} \end{equation}\] donde \(\pi^{\prime}\) es la derivada de \(\pi\). La solución de estas ecuaciones, denotada como \(\mathbf{b}_{MLE}\), es el estimador de máxima verosimilitud. Para la función logit, las ecuaciones de puntaje se reducen a
\[\begin{equation} \frac{\partial }{\partial \boldsymbol \beta}L(\boldsymbol \beta )=\sum\limits_{i=1}^{n}\mathbf{x}_i\left( y_i-\mathrm{\pi }(\mathbf{x} _i^{\mathbf{\prime}}\boldsymbol \beta)\right) =\mathbf{0}, \tag{11.5} \end{equation}\] donde \(\mathrm{\pi }(z)=1/(1+\exp (-z))\).
11.3.2 Inferencia Adicional
Un estimador de la varianza muestral grande de \(\boldsymbol \beta\) puede calcularse tomando las derivadas parciales de las ecuaciones de puntaje. Específicamente, el término \[ \mathbf{I}(\boldsymbol \beta) = - \mathrm{E} \left( \frac{\partial^2} {\partial \boldsymbol \beta ~ \partial \boldsymbol \beta ^{\prime}}L(\boldsymbol \beta) \right) \] es la matriz de información. Como caso especial, usando la función logit y la ecuación (11.5), cálculos sencillos muestran que la matriz de información es \[ \mathbf{I}(\boldsymbol \beta) = \sum\limits_{i=1}^{n} \sigma_i^2 \mathbf{x}_i \mathbf{x}_i^{\prime} \] donde \(\sigma_i^2 = \mathrm{\pi} (\mathbf{x}_i^{\prime} \boldsymbol \beta) (1 - \mathrm{\pi}(\mathbf{x}_i^{\prime} \boldsymbol \beta))\). La raíz cuadrada del \((j+1)\)-ésimo elemento diagonal de esta matriz, evaluado en \(\boldsymbol \beta = \mathbf{b}_{MLE}\), proporciona el error estándar de \(b_{j,MLE}\), denotado como \(se(b_{j,MLE})\).
Para evaluar el ajuste general del modelo, es habitual citar estadísticos de prueba de razón de verosimilitud en modelos de regresión no lineales. Para probar la adecuación general del modelo \(H_0:\boldsymbol \beta=\mathbf{0}\), utilizamos el estadístico \[ LRT=2\times (L(\mathbf{b}_{MLE})-L_0), \] donde \(L_0\) es la log-verosimilitud maximizada solo con el término de intercepto. Bajo la hipótesis nula \(H_0\), este estadístico tiene una distribución chi-cuadrado con \(k\) grados de libertad. La Sección 11.9.3 describe los estadísticos de prueba de razón de verosimilitud con mayor detalle técnico.
Como se describe en la Sección 11.9, las medidas de bondad de ajuste pueden ser difíciles de interpretar en modelos no lineales. Una medida es el llamado \(max-scaled~R^2\), definido como \(R_{ms}^2=R^2/R_{max}^2\), donde \[ R^2=1-\left( \frac{\exp (L_0/n)}{\exp (L(\mathbf{b}_{MLE})/n)}\right) \] y \(R_{max }^2 = 1 - \exp(L_0/n)^2\). Aquí, \(L_0/n\) representa el valor promedio de esta log-verosimilitud.
Otra medida es un “pseudo-\(R^2\)” \[ \frac{L( \mathbf{b}_{MLE}) - L_0}{L_{max}-L_0}, \] donde \(L_0\) y \(L_{max }\) son la log-verosimilitud basada solo en un intercepto y en el máximo alcanzable, respectivamente. Al igual que el coeficiente de determinación, el pseudo-\(R^2\) toma valores entre cero y uno, con valores mayores que indican un mejor ajuste a los datos. Otras versiones del pseudo-\(R^2\) están disponibles en la literatura, véase, por ejemplo, Cameron y Trivedi (1998). Una ventaja de esta medida de pseudo-\(R^2\) es su relación con las pruebas de hipótesis de los coeficientes de regresión.
Ejemplo: Seguridad Laboral. Valletta (1999) estudió la disminución de la seguridad laboral utilizando la base de datos de la Encuesta Panel de Dinámicas de Ingresos (PSID). Aquí consideramos uno de los modelos de regresión presentados por Valletta, basado en una muestra de jefes de hogar masculinos que consta de \(n=24,168\) observaciones durante los años 1976-1992, inclusive. La encuesta PSID registra las razones por las cuales los hombres dejaron su empleo más reciente, incluyendo cierres de planta, “renuncia” y cambios de trabajo por otras razones. Sin embargo, Valletta se centró en los despidos (“lay off” o “despedido”) porque las separaciones involuntarias están asociadas con la inseguridad laboral.
Tabla 11.3 presenta un modelo de regresión probit realizado por Valletta (1999), utilizando los despidos como variable dependiente. Además de las variables explicativas enumeradas en Tabla 11.3, otras variables controladas incluyeron educación, estado civil, número de hijos, raza, años de experiencia laboral a tiempo completo y su cuadrado, afiliación sindical, empleo en el gobierno, salario logarítmico, la tasa de empleo en EE.UU. y ubicación según el área estadística metropolitana de residencia. En la Tabla 11.3, la antigüedad representa los años trabajados en la empresa actual. Además, el empleo en el sector fue medido examinando el empleo según la Encuesta de Precios al Consumidor en 387 sectores de la economía, basada en 43 categorías industriales y nueve regiones del país.
Por un lado, el coeficiente de antigüedad revela que los trabajadores con más experiencia tienen menos probabilidades de ser despedidos. Por otro lado, el coeficiente asociado a la interacción entre antigüedad y la tendencia temporal revela una tasa creciente de despidos para los trabajadores con más experiencia.
La interpretación de los coeficientes de empleo por sector también es de interés. Con una antigüedad promedio de aproximadamente 7.8 años en la muestra, vemos que los hombres con poca antigüedad no se ven muy afectados por los cambios en el empleo por sector. Sin embargo, para los hombres con más experiencia, hay una probabilidad creciente de despido asociada con los sectores de la economía donde el crecimiento disminuye.
Tabla 11.3. Estimaciones de Regresión Probit para Despidos
\[ \small{ \begin{array}{lrr} \hline \textbf{Variable} & \textbf{Estimación del} & \textbf{Error} \\ & \textbf{Parámetro} & \textbf{Estándar} \\ \hline \text{Antigüedad} & -0.084 & 0.010 \\ \text{Tendencia Temporal} & -0.002 & 0.005 \\ \text{Antigüedad*(Tendencia Temporal)} & 0.003 & 0.001 \\ \text{Cambio en el Empleo Logarítmico por Sector} & 0.094 & 0.057 \\ \text{Antigüedad*(Cambio en el Empleo Logarítmico por Sector)} & -0.020 & 0.009 \\ \hline \text{-2 Log Verosimilitud} & 7,027.8 & \\ \text{Pseudo}-R^2 & 0.097 & \\ \hline \end{array} } \]
11.4 Aplicación: Gastos Médicos
Esta sección considera datos de la Encuesta del Panel de Gastos Médicos (MEPS), realizada por la Agencia de Investigación y Calidad de la Salud de EE. UU. MEPS es una encuesta probabilística que proporciona estimaciones representativas a nivel nacional sobre el uso de atención médica, los gastos, las fuentes de pago y la cobertura de seguros para la población civil de EE. UU. Esta encuesta recoge información detallada sobre las personas y cada episodio de atención médica, por tipo de servicios, incluyendo visitas al consultorio del médico, visitas a la sala de emergencias del hospital, visitas ambulatorias al hospital, estancias hospitalarias, visitas a otros proveedores médicos y uso de medicamentos recetados. Esta información detallada permite desarrollar modelos de utilización de atención médica para predecir gastos futuros. Consideramos datos de MEPS del primer panel de 2003 y tomamos una muestra aleatoria de \(n=2,000\) individuos entre 18 y 65 años.
Variable Dependiente
Nuestra variable dependiente es un indicador de gastos positivos por admisiones hospitalarias. En MEPS, las admisiones hospitalarias incluyen personas que fueron admitidas en un hospital y pasaron la noche. En contraste, los eventos ambulatorios incluyen visitas al departamento ambulatorio del hospital, visitas a proveedores en consultorios y visitas a la sala de emergencias, excluyendo servicios dentales. (Los servicios dentales, en comparación con otros tipos de atención médica, son más predecibles y ocurren de manera más regular). Las estancias hospitalarias con la misma fecha de ingreso y alta, conocidas como “estancias de cero noches”, se incluyeron en los recuentos y gastos ambulatorios. Los pagos asociados con visitas a la sala de emergencias que precedieron inmediatamente a una estancia hospitalaria se incluyeron en los gastos hospitalarios. Los medicamentos recetados vinculados a admisiones hospitalarias se incluyeron en los gastos hospitalarios (no en la utilización ambulatoria).
Variables Explicativas
Las variables explicativas que pueden ayudar a explicar la utilización de atención médica se categorizan en factores demográficos, geográficos, de salud, educación y económicos. Los factores demográficos incluyen edad, sexo y etnia. A medida que las personas envejecen, la tasa a la que su salud se deteriora aumenta con la edad; como resultado, la edad tiene un impacto creciente en la demanda de atención médica. El sexo y la etnia pueden tratarse como aproximaciones de la herencia de salud y los hábitos sociales en el mantenimiento de la salud. Para un factor geográfico, usamos la región como una aproximación de la accesibilidad a los servicios de salud y del impacto económico o regional general en el comportamiento de atención médica de los residentes.
Se piensa que la demanda de servicios médicos está influenciada por el estado de salud y la educación de las personas. En MEPS, la salud física y mental autoevaluada, y cualquier limitación funcional o relacionada con la actividad durante el período de la muestra, se utilizan como aproximaciones del estado de salud. La educación tiende a tener un impacto ambiguo en la demanda de servicios de atención médica. Una teoría es que las personas más educadas son más conscientes de los riesgos para la salud, por lo tanto, son más activas en el mantenimiento de su salud; como resultado, las personas educadas pueden ser menos propensas a enfermedades graves que conduzcan a hospitalizaciones. Otra teoría es que las personas con menos educación tienen mayor exposición a riesgos para la salud y, a través de esta exposición, desarrollan una mayor tolerancia a ciertos tipos de riesgos. En MEPS, la educación se aproxima por los títulos recibidos y se clasifica en tres niveles diferentes: menos que secundaria, secundaria, y universidad o superior.
Las covariables económicas incluyen ingresos y cobertura de seguro. Una medida de ingresos en MEPS es el ingreso relativo al nivel de pobreza. Este enfoque es adecuado porque resume los efectos de los diferentes niveles de ingresos en la utilización de atención médica en dólares constantes. La cobertura de seguro también es una variable importante para explicar la utilización de atención médica. Un problema con la cobertura de seguro de salud es que reduce los precios pagados por los asegurados, lo que induce un riesgo moral. La investigación asociada con el Experimento de Seguro de Salud de Rand sugirió empíricamente que los efectos del costo compartido derivados de la cobertura de seguro afectarán principalmente el número de contactos médicos más que la intensidad de cada contacto. Esto motivó nuestra introducción de una variable binaria que toma el valor de 1 si una persona tuvo algún seguro público o privado durante al menos un mes, y 0 de lo contrario.
Estadísticas Descriptivas
Tabla 11.4 describe estas variables explicativas y proporciona estadísticas descriptivas que sugieren sus efectos sobre la probabilidad de gastos hospitalarios positivos. Por ejemplo, vemos que las mujeres tuvieron una mayor utilización general que los hombres. Específicamente, el 10.7% de las mujeres tuvo un gasto positivo durante el año en comparación con solo el 4.7% de los hombres. De manera similar, la utilización varía según otras covariables, lo que sugiere su importancia como predictores de los gastos.
Tabla 11.4. Porcentaje de Gastos Positivos por Variable Explicativa
\[ \scriptsize{ \begin{array}{lllrr} \hline & & & \textbf{Por-} & \textbf{Porcentaje} \\ \textbf{Categoría} & \textbf{Variable} & \textbf{Descripción} & \textbf{centaje} & \textbf{Gastos} \\ & & & \textbf{de datos} & \textbf{Positivos} \\ \hline \text{Demografía} & AGE & \text{Edad en años entre} \\ & & \text{ 18 a 65 (media: 39.0)} \\ & GENDER & 1 \text{si mujer} & 52.7 & 10.7 \\ & & \text{0 si hombre} & 47.3 & 4.7\\ \text{Etnia} & ASIAN & \text{1 si asiático} & 4.3 & 4.7 \\ & BLACK & \text{1 si negro} & 14.8 & 10.5 \\ & NATIVE & \text{1 si nativo} & 1.1 & 13.6 \\ & WHITE & \text{Nivel de referencia} & 79.9 & 7.5 \\ \text{Región} & NORTHEAST & 1 \text{si noreste} & 14.3 & 10.1 \\ & MIDWEST & 1 \text{si medio oeste} & 19.7 & 8.7 \\ & SOUTH & 1 \text{si sur} & 38.2 & 8.4 \\ & WEST & \text{Nivel de referencia} &27.9 & 5.4 \\ \hline \text{Educación} & \text{COLLEGE} & 1 \text{si universidad o grado superior} & 27.2 & 6.8 \\ & HIGHSCHOOL & 1 \text{si grado de secundaria} & 43.3 & 7.9\\ & \text{Nivel de referencia } & & 29.5 & 8.8\\ & \text{ es menor que grado} & & \\ & \text{ de secundaria} & & \\ \hline \text{Salud } & POOR & \text{1 si pobre} & 3.8 & 36.0 \\ \ \ \text{autoevaluada} & FAIR & \text{1 si regular} & 9.9 & 8.1 \\ \ \ \text{física} & GOOD & \text{1 si buena} & 29.9 & 8.2 \\ \ \ \text{salud}& VGOOD & \text{1 si muy buena} & 31.1 & 6.3 \\ & \text{Nivel de referencia} & & 25.4 & 5.1 \\ & ~~~\text{ es excelente salud} & & \\ \text{Salud mental} & MNHPOOR & \text{1 si pobre o regular} & 7.5 & 16.8 \\ \ \ \text{autoevaluada} & & \text{0 si buena a excelente salud mental} & 92.6 & 7.1 \\ \text{Cualquier} & ANYLIMIT & \text{1 si cualquier limitación}& 22.3 & 14.6 \\ \ \ \ \text{ limitación} & & \ \ \ \text{funcional/actividad}& & \\ \ \ \text{en la actividad} & & \text{0 si no hay limitación} & 77.7 & 5.9 \\ \hline \text{Ingresos} & HINCOME & \text{1 si ingresos altos} & 31.6 & 5.4 \\ \ \ \text{comparado con} & MINCOME & \text{1 si ingresos medios} & 29.9 & 7.0 \\ \ \ \text{nivel de pobreza} & LINCOME & \text{1 si ingresos bajos} & 15.8 & 8.3 \\ & NPOOR & \text{1 si casi pobre} & 5.8 & 9.5 \\ & \text{Nivel de referencia} && 17.0 & 13.0 \\ & ~~~\text{ es pobre/negativo} & & \\ \hline \text{Seguro} & INSURE & \text{1 si cubierto por seguro } & 77.8 & 9.2 \\ \ \ \text{de salud} & & \ \ \text{público/privado en } & & \\ & & \ \ \text{cualquier mes de 2003} & & \\ & & \text{0 si no tiene seguro de salud en 2003} & 22.3 & 3.1 \\ \hline Total & & & 100.0 & 7.9 \\ \hline \end{array} } \]
Código R para Generar la Tabla 11.4
La Tabla 11.5 resume el ajuste de varios modelos de regresión binaria. Los ajustes se informan en la columna “Modelo Completo” para todas las variables utilizando la función logit. Los \(t\)-ratios para muchas de las variables explicativas superan dos en valor absoluto, lo que sugiere que son predictores útiles. A partir de una inspección de estos \(t\)-ratios, uno podría considerar un modelo más parsimonioso eliminando las variables estadísticamente insignificantes. La Tabla 11.5 muestra un “Modelo Reducido,” en el cual las variables de edad y estado de salud mental han sido eliminadas. Para evaluar su significancia conjunta, podemos calcular un estadístico de prueba de razón de verosimilitud como el doble del cambio en la log-verosimilitud. Esto resulta ser solo \(2\times \left( -488.78-(-488.69)\right) =0.36.\) Comparando esto con una distribución chi-cuadrado con \(df=2\) grados de libertad, obtenemos un valor-\(p=0.835\), lo que indica que los parámetros adicionales para la edad y el estado de salud mental no son estadísticamente significativos. La Tabla 11.5 también proporciona los ajustes del modelo probit. Aquí, vemos que los resultados son similares a los del modelo logit, según el signo de los coeficientes y su significancia, lo que sugiere que para esta aplicación hay poca diferencia entre las dos especificaciones.
Tabla 11.5. Comparación de Modelos de Regresión Binaria
\[ \scriptsize{ \begin{array}{l|rr|rr|rr} \hline & \text{Logistic} & & \text{Logistic} &&\text{Probit} \\ \hline & \text{Full Model} & &\text{Reduced Model} && \text{Reduced Model} \\ & \text{Parameter} & & \text{Parameter} & & \text{Parameter} & \\ \text{Effect} & \text{Estimate} & t\text{-ratio}o & \text{Estimate} & t\text{-rati}o & \text{Estimate} & t\text{-ratio} \\ \hline Intercept & -4.239 & -8.982 & -4.278 & -10.094 & -2.281 & -11.432 \\ AGE & -0.001 & -0.180 & & & & \\ GENDER & 0.733 & 3.812 & 0.732 & 3.806 & 0.395 & 4.178 \\ ASIAN & -0.219 & -0.411 & -0.219 & -0.412 & -0.108 & -0.427 \\ BLACK & -0.001 & -0.003 & 0.004 & 0.019 & 0.009 & 0.073 \\ NATIVE & 0.610 & 0.926 & 0.612 & 0.930 & 0.285 & 0.780 \\ NORTHEAST & 0.609 & 2.112 & 0.604 & 2.098 & 0.281 & 1.950 \\ MIDWEST & 0.524 & 1.904 & 0.517 & 1.883 & 0.237 & 1.754 \\ SOUTH & 0.339 & 1.376 & 0.328 & 1.342 & 0.130 & 1.085 \\ \hline COLLEGE & 0.068 & 0.255 & 0.070 & 0.263 & 0.049 & 0.362 \\ HIGHSCHOOL & 0.004 & 0.017 & 0.009 & 0.041 & 0.003 & 0.030 \\ \hline POOR & 1.712 & 4.385 & 1.652 & 4.575 & 0.939 & 4.805 \\ FAIR & 0.136 & 0.375 & 0.109 & 0.306 & 0.079 & 0.450 \\ GOOD & 0.376 & 1.429 & 0.368 & 1.405 & 0.182 & 1.412 \\ VGOOD & 0.178 & 0.667 & 0.174 & 0.655 & 0.094 & 0.728 \\ MNHPOOR & -0.113 & -0.369 & & & & \\ ANYLIMIT & 0.564 & 2.680 & 0.545 & 2.704 & 0.311 & 3.022 \\ \hline HINCOME & -0.921 & -3.101 & -0.919 & -3.162 & -0.470 & -3.224 \\ MINCOME & -0.609 & -2.315 & -0.604 & -2.317 & -0.314 & -2.345 \\ LINCOME & -0.411 & -1.453 & -0.408 & -1.449 & -0.241 & -1.633 \\ NPOOR & -0.201 & -0.528 & -0.204 & -0.534 & -0.146 & -0.721 \\ INSURE & 1.234 & 4.047 & 1.227 & 4.031 & 0.579 & 4.147 \\ \hline Log-Likelihood & -488.69 && -488.78 && -486.98 \\ \textit{AIC} & 1,021.38 && 1,017.56 && 1,013.96 \\ \hline \end{array} } \]
Código R para Generar la Tabla 11.5
11.5 Variables Dependientes Nominales
Ahora consideramos una respuesta que es una variable categórica no ordenada, también conocida como variable dependiente nominal. Suponemos que la variable dependiente \(y\) puede tomar los valores \(1, 2, \ldots , c,\) correspondientes a \(c\) categorías. Cuando \(c>2\), nos referimos a los datos como “multicategoría”, también conocidos como policótomos o policitomos.
En muchas aplicaciones, las categorías de respuesta corresponden a un atributo poseído o a elecciones hechas por individuos, hogares o empresas. Algunas aplicaciones incluyen:
- Elección de empleo, como en Valletta (1999)
- Modo de transporte, como en el trabajo clásico de McFadden (1978)
- Tipo de seguro de salud, como en Browne y Frees (2007).
Para una observación del sujeto \(i\), denotamos la probabilidad de elegir la categoría \(j\) como \(\pi_{ij}= \mathrm{Pr}(y_i = j)\), de modo que \(\pi_{i1}+\cdots+\pi_{ic}=1\). En general, modelaremos estas probabilidades como una función (conocida) de parámetros y utilizaremos la estimación de máxima verosimilitud para la inferencia estadística. Sea \(y_{ij}\) una variable binaria que es 1 si \(y_i=j\). Extendiendo la ecuación (11.2) a \(c\) categorías, la verosimilitud para el sujeto \(i\) es:
\[ \prod_{j=1}^c \left( \pi_{i,j} \right)^{y_{i,j}} =\left\{ \begin{array}{cc} \pi_{i,1} & \mathrm {if}~ y_i = 1 \\ \pi_{i,2} & \mathrm {if}~ y_i = 2 \\ \vdots & \vdots \\ \pi_{i,c} & \mathrm {if}~ y_i = c \\ \end{array} \right. . \] Por lo tanto, suponiendo independencia entre las observaciones, la verosimilitud total es
\[ L = \sum_{i=1}^n \sum_{j=1}^c y_{i,j}~ \mathrm{ln}~ \pi_{i,j} . \] Con este marco, la estimación estándar de máxima verosimilitud está disponible (Sección 11.9). Por lo tanto, nuestra tarea principal es especificar una forma apropiada para \(\pi\).
11.5.1 Logit Generalizado
Al igual que la regresión lineal estándar, los modelos de logit generalizado emplean combinaciones lineales de variables explicativas de la forma: \[\begin{equation} V_{i,j} = \mathbf{x}_i^{\prime} \boldsymbol \beta_j . \tag{11.6} \end{equation}\] Debido a que las variables dependientes no son numéricas, no podemos modelar la respuesta \(y\) como una combinación lineal de variables explicativas más un error. En su lugar, utilizamos las probabilidades \[\begin{equation} \mathrm{Pr} \left(y_i = j \right) = \pi_{i,j} = \frac {\exp (V_{i,j})}{\sum_{k=1}^c \exp(V_{i,k})} . \tag{11.7} \end{equation}\] Tenga en cuenta aquí que \(\boldsymbol \beta_j\) es el vector correspondiente de parámetros que puede depender de la alternativa \(j\), mientras que las variables explicativas \(\mathbf{x}_i\) no. Para que las probabilidades sumen uno, una normalización conveniente para este modelo es \(\boldsymbol \beta_c =\mathbf{0}\). Con esta normalización y el caso especial de \(c = 2\), el logit generalizado se reduce al modelo de logit introducido en la Sección 11.2.
Interpretaciones de Parámetros
Ahora describimos una interpretación de los coeficientes en los modelos de logit generalizado, similar al modelo logístico. De las ecuaciones (11.6) y (11.7), tenemos \[ \mathrm{ln}~ \frac{\mathrm{Pr} \left(y_i = j \right)} {\mathrm{Pr} \left(y_i = c \right)} = V_{i,j} - V_{i,c} =\mathbf{x}_i^{\prime} \boldsymbol \beta_j . \] El lado izquierdo de esta ecuación se interpreta como el logaritmo de las probabilidades de elegir la opción \(j\) en comparación con la opción \(c\). Por lo tanto, podemos interpretar \(\boldsymbol \beta_j\) como el cambio proporcional en la razón de probabilidad.
Los logits generalizados tienen una interesante estructura anidada que exploraremos brevemente en la Sección 11.5.3. Es decir, es fácil comprobar que, condicional a no elegir la primera categoría, la forma de Pr(\(y_i = j| y_i \neq 1\)) tiene una forma de logit generalizado en la ecuación (11.7). Además, si \(j\) y \(h\) son alternativas diferentes, observamos que
\[\begin{eqnarray*} \mathrm{Pr}(y_i = j| y_i=j ~\mathrm{or}~ y_i=h) &=&\frac{\mathrm{Pr}(y_i = j)}{\mathrm{Pr}(y_i = j)+\mathrm{Pr}(y_i = h)} =\frac{\mathrm{exp}(V_{i,j})}{\mathrm{exp}(V_{i,j})+\mathrm{exp}(V_{i,h})} \\ &=&\frac{1}{1+\mathrm{exp}(\mathbf{x}_i^{\prime}(\boldsymbol \beta _h - \boldsymbol \beta_j))} . \end{eqnarray*}\]
Esto tiene una forma de logit que se introdujo en la Sección 11.2.
Caso Especial - Modelo con solo intercepto. Para desarrollar intuición, ahora consideramos el modelo con solo interceptos. Así, sea \(\mathbf{x}_i = 1\) y \(\boldsymbol \beta_j = \beta_{0,j} = \alpha_j\). Con la convención de que \(\alpha_c=0\), tenemos \[ \mathrm{Pr} \left(y_i = j \right) = \pi_{i,j} = \frac {e^{\alpha_j}}{e^{\alpha_1}+e^{\alpha_2}+\cdots+e^{\alpha_{c-1}}+1} \] y \[ \mathrm{ln}~ \frac{\mathrm{Pr} \left(y_i = j \right)} {\mathrm{Pr} \left(y_i = c \right)} = \alpha_j. \] A partir de la segunda relación, podemos interpretar el \(j\)-ésimo intercepto \(\alpha_j\) como las probabilidades logarítmicas de elegir la alternativa \(j\) en comparación con la alternativa \(c\).
Ejemplo: Seguridad Laboral - Continuación. Esta es una continuación del ejemplo de la Sección 11.2 sobre los determinantes de la rotación laboral, basado en el trabajo de Valletta (1999). El primer análisis de estos datos consideró solo la variable dependiente binaria de despido, ya que este resultado es la principal fuente de inseguridad laboral. Valletta (1999) también presentó resultados de un modelo logit generalizado, su principal motivación fue que la teoría económica que describe la rotación laboral implica que otras razones para dejar un trabajo pueden afectar las probabilidades de despido.
Para el modelo logit generalizado, la variable de respuesta tiene \(c = 5\) categorías: despido, dejó el trabajo debido al cierre de plantas, “renunció”, cambió de trabajo por otras razones y no hubo cambio en el empleo. La categoría de “no hubo cambio en el empleo” es la omitida en Tabla 11.6. Las variables explicativas del logit generalizado son las mismas que en la regresión probit; las estimaciones resumidas en la Tabla 11.1 se reproducen aquí para mayor conveniencia.
Tabla 11.6 muestra que la rotación disminuye a medida que aumenta la antigüedad. Para ilustrar, considere a un hombre típico en la muestra de 1992 donde tenemos tiempo = 16 y nos enfocamos en las probabilidades de despido. Para este valor de tiempo, el coeficiente asociado con la antigüedad para el despido es -0.221 + 16 (0.008) = -0.093 (debido al término de interacción). A partir de esto, interpretamos que un año adicional de antigüedad implica que la probabilidad de despido es exp(-0.093) = 91% de lo que sería de otra manera, lo que representa una disminución del 9%.
Tabla 11.6 también muestra que los coeficientes generalizados asociados con el despido son similares a los ajustes del modelo probit.
Los errores estándar también son cualitativamente similares, aunque más altos para los logit generalizados en comparación con el modelo probit. En particular, nuevamente vemos que el coeficiente asociado con la interacción entre la antigüedad y la tendencia del tiempo revela una tasa de despido en aumento para los trabajadores con experiencia. Lo mismo ocurre con la tasa de renuncia.
Tabla 11.6. Estimaciones de Regresión Logit Generalizado y Probit para la Rotación Laboral
\[ \small{ \begin{array}{lcrrrr} \hline & \textbf{Probit} & &\textbf{Logit} &\textbf{Generalizado} &\textbf{Modelo} \\ & \text{Regresión} & & \text{Cierre de} & \text{Otras} & \\ \text{Variable} & \text{Modelo} & \text{Despido} & \text{Plantas} & \text{razones} & \text{Renuncia} \\ & \text{(Despido)}\\ \hline \text{Antigüedad} & -0.084 & -0.221 & -0.086 & -0.068 & -0.127 \\ & (0.010) & (0.025) & (0.019) & (0.020) & (0.012) \\ \text{Tendencia Temporal} & -0.002 & -0.008 & -0.024 & 0.011 & -0.022 \\ & (0.005) & (0.011) & (0.016) & (0.013) & (0.007)\\ \text{Antigüedad (Tendencia Temporal)} & 0.003 & 0.008 & 0.004 & -0.005 & 0.006 \\ & (0.001) & (0.002) & (0.001) & (0.002) & (0.001) \\ \text{Cambio en Logaritmo} & 0.094 & 0.286 & 0.459 & -0.022 & 0.333 \\ ~~\text{de Empleo en el Sector} & (0.057) & (0.123) & (0.189) & (0.158) & (0.082) \\ \text{Antigüedad (Cambio en Logaritmo} & -0.020 & -0.061 & -0.053 & -0.005 & -0.027 \\ ~~\text{de Empleo en el Sector)} & (0.009) & (0.023) & (0.025) & (0.025) & (0.012) \\ \hline \end{array} } \]
Notas: Errores estándar en paréntesis. La categoría omitida es la de no cambio en el empleo para el logit generalizado. Otras variables controladas incluyen educación, estado civil, número de hijos, raza, años de experiencia laboral a tiempo completo y su cuadrado, membresía sindical, empleo en el gobierno, salario logarítmico, la tasa de empleo en EE.UU. y ubicación.
11.5.2 Logit Multinomial
Similar al ecuación (11.6), una combinación lineal alternativa de las variables explicativas es \[\begin{equation} V_{i,j} = \mathbf{x}_{i,j}^{\prime} \boldsymbol \beta, \tag{11.8} \end{equation}\] donde \(\mathbf{x}_{i,j}\) es un vector de variables explicativas que depende de la \(j\)-ésima alternativa mientras que los parámetros \(\boldsymbol \beta\) no. Utilizando las expresiones en las ecuaciones (11.7) y (11.8) se forma la base del modelo logit multinomial, también conocido como el modelo logit condicional (McFadden, 1974). Con esta especificación, la log-verosimilitud total es \[ L = \sum_{i=1}^n \sum_{j=1}^c y_{i,j}~ \mathrm{ln}~ \pi_{i,j} = \sum_{i=1}^n \left[ \sum_{j=1}^c y_{i,j} \mathbf{x}_{i,j}^{\prime} \boldsymbol \beta \ - \mathrm{ln} \left(\sum_{k=1}^c \mathrm{exp}(\mathbf{x}_{i,k}^{\prime} \boldsymbol \beta) \right) \right]. \] Esta expresión directa para la verosimilitud permite realizar fácilmente la inferencia por máxima verosimilitud.
El modelo logit generalizado es un caso especial del modelo logit multinomial. Para ver esto, considere las variables explicativas \(\mathbf{x}_i\) y los parámetros \(\boldsymbol \beta_j\), cada uno de dimensión \(k\times 1\). Defina \[ \mathbf{x}_{i,j} = \left( \begin{array}{c} \mathbf{0} \\ \vdots \\ \mathbf{0} \\ \mathbf{x}_i \\ \mathbf{0} \\ \vdots \\ \mathbf{0} \\ \end{array}\right) ~~~ \mathrm{y}~~~ \boldsymbol \beta = \left( \begin{array}{c} \boldsymbol \beta_1 \\ \boldsymbol \beta_2 \\ \vdots \\ \boldsymbol \beta_c \\ \end{array} \right). \] Específicamente, \(\mathbf{x}_{i,j}\) se define como \(j-1\) vectores nulos (cada uno de dimensión \(k\times 1\)), seguido por \(\mathbf{x}_i\) y luego seguido por \(c-j\) vectores nulos. Con esta especificación, tenemos \(\mathbf{x}_{i,j}^{\prime} \boldsymbol \beta =\mathbf{x}_i^{\prime} \boldsymbol \beta_j\). Así, un paquete estadístico que realiza estimaciones logit multinomiales también puede realizar estimaciones logit generalizadas mediante la codificación apropiada de variables explicativas y parámetros. Otra consecuencia de esta conexión es que algunos autores usan el término logit multinomial cuando se refieren al modelo logit generalizado.
Además, mediante esquemas de codificación similares, los modelos logit multinomiales también pueden manejar combinaciones lineales de la forma: \[ V_i = \mathbf{x}_{i,1,j}^{\prime} \boldsymbol \beta + \mathbf{x}_{i,2}^{\prime} \boldsymbol \beta_j . \] Aquí, \(\mathbf{x}_{i,1,j}\) son variables explicativas que dependen de la alternativa, mientras que \(\mathbf{x}_{i,2}\) no. De manera similar, \(\boldsymbol \beta_j\) son parámetros que dependen de la alternativa, mientras que \(\boldsymbol \beta\) no. Este tipo de combinación lineal es la base de un modelo logit mixto. Al igual que con los logits condicionales, es común elegir un conjunto de parámetros como base y especificar \(\boldsymbol \beta_c = \mathbf{0}\) para evitar redundancias.
Para interpretar los parámetros del modelo logit multinomial, podemos comparar las alternativas \(h\) y \(k\) usando las ecuaciones (11.7) y (11.8), obteniendo \[ \mathrm{ln}~ \frac{\mathrm{Pr} \left(y_i = h \right)} {\mathrm{Pr} \left(y_i = k \right)} = (\mathbf{x}_{i,h}-\mathbf{x}_{i,k}) ^{\prime} \boldsymbol \beta . \] Así, podemos interpretar \(\beta_j\) como el cambio proporcional en la razón de probabilidades, donde el cambio es el valor de la \(j\)-ésima variable explicativa, pasando de la alternativa \(k\) a la \(h\).
Con la ecuación (11.7), note que \(\pi_{i,1} / \pi_{i,2} = \mathrm{exp}(V_{i,1}) /\mathrm{exp}(V_{i,2})\). Esta razón no depende de los valores subyacentes de las otras alternativas, \(V_{i,j}\), para \(j=3, \ldots, c\). Esta característica, llamada independencia de alternativas irrelevantes, puede ser una desventaja del modelo logit multinomial para algunas aplicaciones.
Ejemplo: Elección de Seguro de Salud. Para ilustrar, Browne y Frees (2007) examinaron \(c=4\) opciones de seguro de salud, que consistían en:
- \(y=1\) - un individuo cubierto por seguro grupal,
- \(y=2\) - un individuo cubierto por seguro privado, no grupal,
- \(y=3\) - un individuo cubierto por seguro gubernamental, pero no privado, o
- \(y=4\) - un individuo no cubierto por seguro de salud.
Sus datos sobre cobertura de seguro de salud provinieron del suplemento de marzo de la Encuesta de Población Actual (CPS, por sus siglas en inglés), realizada por la Oficina de Estadísticas Laborales. Browne y Frees (2007) analizaron aproximadamente 10,800 hogares de personas solteras por año, cubriendo de 1988 a 1995, lo que dio un total de \(n=86,475\) observaciones. Examinaron si las restricciones de suscripción, leyes aprobadas para prohibir que los aseguradores discriminen, facilitan o desalientan el consumo de seguros de salud. Se centraron en las leyes de discapacidad que prohibían a los aseguradores utilizar la discapacidad física como criterio de suscripción.
La Tabla 11.7 sugiere que las leyes de discapacidad tienen poco efecto en el comportamiento promedio de compra de seguro de salud. Para ilustrar, para los individuos encuestados con las leyes de discapacidad en vigor, el 57.6% compró seguro de salud grupal en comparación con el 59.3% de aquellos donde las restricciones no estaban en vigor. De manera similar, el 19.9% no tenía seguro cuando las restricciones de discapacidad estaban en vigor en comparación con el 20.1% cuando no lo estaban. En términos de probabilidades, cuando las restricciones de discapacidad estaban en vigor, las probabilidades de comprar un seguro de salud grupal en comparación con quedar sin seguro son 57.6/19.9 = 2.895. Cuando las restricciones de discapacidad no estaban en vigor, las probabilidades son 2.946. La razón de probabilidades, 2.895/2.946 = 0.983, indica que hay poco cambio en las probabilidades cuando se compara si las restricciones de discapacidad estaban en vigor o no.
| Ley de Discapacidad en Vigor | Número | Sin Seguro | No Grupal | Gubernamental | Grupal | Prob. Comparativa Grupal vs. Sin Seguro | Razón de Probabilidades |
|---|---|---|---|---|---|---|---|
| No | 82246 | 20.1 | 12.2 | 8.4 | 59.3 | 2.946 | |
| Sí | 4229 | 19.9 | 10.1 | 12.5 | 57.6 | 2.895 | 0.983 |
| Total | 86475 | 20.1 | 12.1 | 8.6 | 59.2 |
En contraste, la Tabla 11.8 sugiere que las leyes de discapacidad pueden tener efectos importantes en el comportamiento promedio de compra de seguro de salud de subgrupos seleccionados de la muestra. La Tabla 11.8 muestra el porcentaje de personas sin seguro y las probabilidades de adquirir un seguro grupal (comparado con estar sin seguro) para subgrupos seleccionados. Para ilustrar, para personas con discapacidad, las probabilidades de adquirir un seguro grupal son 1.329 veces más altas cuando las restricciones de discapacidad están en vigor. La Tabla 11.7 sugiere que las restricciones de discapacidad no tienen efecto; esto puede ser cierto al observar toda la muestra. Sin embargo, al examinar subgrupos, la Tabla 11.8 muestra que podemos ver efectos importantes asociados con las restricciones legales de suscripción que no son evidentes al observar los promedios en toda la muestra.
| Subgrupos Seleccionados | Ley de Discapacidad en Vigor | Número | Porcentaje Grupal | Porcentaje Sin Seguro | Prob. Comparativa Grupal vs. Sin Seguro | Razón de Probabilidades |
|---|---|---|---|---|---|---|
| Sin Discapacidad | No | 72150 | 64.2 | 20.5 | 3.134 | |
| Sin Discapacidad | Sí | 3649 | 63.4 | 21.2 | 2.985 | 0.952 |
| Con Discapacidad | No | 10096 | 24.5 | 17.6 | 1.391 | |
| Con Discapacidad | Sí | 580 | 21 | 11.4 | 1.848 | 1.329 |
Hay muchas formas de seleccionar subgrupos de interés. Con un gran conjunto de datos de \(n=86,475\) observaciones, probablemente se podrían elegir subgrupos para confirmar casi cualquier hipótesis. Además, existe la preocupación de que los datos de la CPS pueden no proporcionar una muestra representativa de las poblaciones estatales. Por lo tanto, es habitual utilizar técnicas de regresión para “controlar” las variables explicativas, como la discapacidad física.
La Tabla 11.9 presenta los principales resultados de un modelo logit multinomial con muchas variables de control incluidas. Se incluyó una variable dummy para cada uno de los 50 estados (el Distrito de Columbia es un “estado” en este conjunto de datos, por lo que necesitamos \(51-1=50\) variables dummy). Estas variables fueron sugeridas en la literatura y son descritas con más detalle en Browne y Frees (2007). Incluyen el género del individuo, estado civil, raza, nivel educativo, si es trabajador independiente o no y si el individuo trabajó a tiempo completo, a tiempo parcial o no trabajó.
En la Tabla 11.9, “Ley” se refiere a la variable binaria que es 1 si una restricción legal estaba en vigor y “Discapacidad” es una variable binaria que es 1 si un individuo tiene una discapacidad física. Por lo tanto, la interacción “Ley*Discapacidad” informa sobre el efecto de una restricción legal en una persona con discapacidad física. La interpretación es similar a la de la Tabla 11.8. Específicamente, interpretamos el coeficiente 1.419 como que las personas con discapacidad son un 41.9% más propensas a adquirir un seguro de salud grupal comparado con no adquirir ningún seguro, cuando la restricción de suscripción por discapacidad está en vigor. De manera similar, las personas sin discapacidad son un 21.2% (\(=1/0.825 - 1\)) menos propensas a adquirir un seguro de salud grupal comparado con no adquirir ningún seguro, cuando la restricción de suscripción por discapacidad está en vigor. Este resultado sugiere que las personas sin discapacidad son más propensas a quedar sin seguro como resultado de las prohibiciones sobre el uso del estado de discapacidad como criterio de suscripción. En general, los resultados son estadísticamente significativos, confirmando que esta restricción legal tiene un impacto en el consumo de seguros de salud.
| Grupal vs. Sin Seguro | No Grupal vs. Sin Seguro | Gubernamental vs. Sin Seguro | Grupal vs. No Grupal | Grupal vs. Gubernamental | No Grupal vs. Gubernamental | |
|---|---|---|---|---|---|---|
| Ley \(\times\) Sin Discapacidad | 0.825 | 1.053 | 1.010 | 0.784 | 0.818 | 1.043 |
| \(p\)-Valor | 0.001 | 0.452 | 0.900 | 0.001 | 0.023 | 0.677 |
| Ley \(\times\) Con Discapacidad | 1.419 | 0.953 | 1.664 | 1.490 | 0.854 | 0.573 |
| \(p\)-Valor | 0.062 | 0.789 | 0.001 | 0.079 | 0.441 | 0.001 |
Notas: La regresión incluye 150 (\(=50 \times 3\)) efectos específicos por estado, varias variables continuas (edad, educación e ingresos, así como términos de orden superior) y variables categóricas (como raza y año).
11.5.3 Logit Anidado
Para mitigar el problema de la independencia de alternativas irrelevantes en los logits multinomiales, ahora introducimos un tipo de modelo jerárquico conocido como un logit anidado. Para interpretar el modelo logit anidado, en la primera etapa se elige una alternativa (digamos la primera alternativa) con probabilidad \[\begin{equation} \pi_{i,1} = \mathrm{Pr}(y_i = 1) = \frac{\mathrm{exp}(V_{i,1})}{\mathrm{exp}(V_{i,1})+ \left[ \sum_{k=2}^c \mathrm{exp}(V_{i,k}/ \rho) \right]^{\rho}} . \tag{11.9} \end{equation}\] Luego, condicionado a no elegir la primera alternativa, la probabilidad de elegir cualquiera de las otras alternativas sigue un modelo logit multinomial con probabilidades \[\begin{equation} \frac{\pi_{i,j}}{1-\pi_{i,1}} = \mathrm{Pr}(y_i = j | y_i \neq 1) = \frac{\mathrm{exp}(V_{i,j}/ \rho)}{\sum_{k=2}^c \mathrm{exp}(V_{i,k}/ \rho) }, ~~~j=2, \ldots, c . \tag{11.10} \end{equation}\] En las ecuaciones (11.9) y (11.10), el parámetro \(\rho\) mide la asociación entre las elecciones \(j = 2, \ldots, c\). El valor de \(\rho=1\) se reduce al modelo logit multinomial, lo que interpretamos como independencia de alternativas irrelevantes. También interpretamos Prob(\(y_i = 1\)) como un promedio ponderado de los valores de la primera elección y las otras. Condicionado a no elegir la primera categoría, la forma de \(\mathrm{Pr}(y_i = j| y_i \neq 1)\) en la ecuación (11.10) tiene la misma forma que el logit multinomial.
La ventaja del logit anidado es que generaliza el modelo logit multinomial de manera que ya no tenemos el problema de la independencia de alternativas irrelevantes. Una desventaja, señalada por McFadden (1981), es que solo se observa una elección; por lo tanto, no sabemos qué categoría pertenece a la primera etapa de la anidación sin una teoría adicional sobre el comportamiento de elección. No obstante, el logit anidado generaliza el logit multinomial al permitir estructuras de “dependencia” alternativas. Es decir, se puede ver el logit anidado como una alternativa robusta al logit multinomial y examinar cada una de las categorías en la primera etapa de la anidación.
11.6 Variables Dependientes Ordinales
Ahora consideramos una respuesta que es una variable categórica ordenada, también conocida como una variable dependiente ordinal. Para ilustrar, cualquier tipo de respuesta de encuesta en la que se califique la impresión en una escala de siete puntos que va desde “muy insatisfecho” hasta “muy satisfecho” es un ejemplo de una variable ordinal.
Ejemplo: Elección de Plan de Salud. Pauly y Herring (2007) examinaron \(c=4\) opciones de tipos de planes de salud, que consistían en:
- \(y=1\) - una organización para el mantenimiento de la salud (HMO),
- \(y=2\) - un plan de punto de servicio (POS),
- \(y=3\) - una organización de proveedores preferidos (PPO) o
- \(y=4\) - un plan de pago por servicio (FFS).
Un plan FFS es el menos restrictivo, permitiendo a los afiliados ver a los proveedores de atención médica (como médicos de atención primaria) por una tarifa que refleja el costo de los servicios prestados. El plan PPO es el siguiente menos restrictivo; este plan generalmente utiliza pagos FFS pero los afiliados generalmente deben elegir de una lista de “proveedores preferidos”. Pauly y Herring (2007) consideraron los planes POS y HMO como el tercer y cuarto menos restrictivo, respectivamente. Un HMO a menudo utiliza la capitación (una tarifa fija por persona) para reembolsar a los proveedores, restringiendo a los afiliados a una red de proveedores. En contraste, un plan POS da a los afiliados la opción de ver a proveedores fuera de la red de HMO (por una tarifa adicional).
11.6.1 Logit Acumulativo
Los modelos de variables dependientes ordinales se basan en probabilidades acumulativas de la forma \[ \mathrm{Pr} ( y \le j ) = \pi_1 + \cdots + \pi_j, ~ ~ j=1, \ldots, c . \] En esta sección, usamos logits acumulativos \[\begin{equation} \mathrm{logit}\left(\mathrm{Pr} ( y \le j ) \right) = \mathrm{ln} \left(\frac{\Pr ( y \le j )}{1-\Pr ( y \le j )} \right) = \mathrm{ln} \left(\frac{\pi_1 + \cdots + \pi_j}{\pi_{j+1} + \cdots + \pi_c} \right) . \tag{11.11} \end{equation}\]
El modelo de logit acumulativo más simple es \[ \mathrm{logit}\left(\Pr ( y \le j ) \right) = \alpha_j \] que no utiliza ninguna variable explicativa. Los parámetros de “punto de corte” \(\alpha_j\) son no decrecientes, de modo que \(\alpha_1 \le \alpha_2 \le \ldots \le \alpha_c,\) reflejando la naturaleza acumulativa de la función de distribución \(\mathrm{Pr} ( y \le j )\).
El modelo de razones proporcionales incorpora variables explicativas. Con este modelo, los logits acumulativos se expresan como \[\begin{equation} \mathrm{logit}\left(\Pr ( y \le j ) \right) = \alpha_j + \mathbf{x}_i^{\prime} \boldsymbol \beta . \tag{11.12} \end{equation}\] Este modelo proporciona interpretaciones de los parámetros similares a las descritas para la regresión logística en la Sección 11.4. Por ejemplo, si la variable \(x_1\) es continua, entonces como en la ecuación (11.1) tenemos \[ \beta_1 = \frac{\partial }{\partial x_{i1}}\left( \alpha_j + \mathbf{x}_i^{\prime}\boldsymbol \beta \right) = \frac{\frac{\partial }{\partial x_{i1}}\Pr (y_i \le j|\mathbf{x}_i)/\left( 1-\Pr (y_ile j|\mathbf{x}_i)\right) }{\Pr (y_ile j|\mathbf{x}_i)/\left( 1-\Pr (y_ile j|\mathbf{x}_i)\right) }. \] Por lo tanto, podemos interpretar \(\beta_1\) como el cambio proporcional en la razón de probabilidades acumulativas.
Ejemplo: Elección de Plan de Salud - Continuación. Pauly y Herring utilizaron datos de las Encuestas del Estudio de Seguimiento Comunitario de Hogares (CTS-HS) de 1996-1997 y 1998-1999 para estudiar la demanda de seguros de salud. Esta es una encuesta representativa a nivel nacional que contiene más de 60,000 individuos por período. Como una medida de la demanda, Pauly y Herring examinaron la elección de plan de salud, razonando que los individuos que eligieron (a través de empleo o membresía en una asociación) planes menos restrictivos buscaban una mayor protección para la atención médica. (También analizaron otras medidas, incluyendo el número de restricciones impuestas a los planes y la cantidad de compartición de costos.) Tabla 11.10 proporciona los determinantes de la elección de plan de salud basado en \(n=34,486\) individuos que tenían seguro de salud grupal, de entre 18 y 64 años sin seguro público. Pauly y Herring también compararon estos resultados con aquellos que tenían seguro de salud individual para entender las diferencias en los determinantes entre estos dos mercados.
Tabla 11.10. Modelo de Logit Acumulativo para la Elección de Plan de Salud
\[ \small{ \begin{array}{llll} \hline \textbf{Variable} & \textbf{Razón de } & \textbf{Variable} & \textbf{Razón de} \\ & \textbf{ Probabilidades} & & \textbf{Probabilidades} \\ \hline \text{Edad} & 0.992^{***} & \text{Hispano} & 1.735^{***} \\ \text{Mujer} & 1.064^{***} & \text{Tomador de riesgos} & 0.967 \\ \text{Tamaño de la familia} & 0.985 & \text{Fumador} & 1.055^{***} \\ \text{Ingresos familiares} & 0.963^{***} & \text{Salud regular/mala} & 1.056 \\ \text{Educación} & 1.006 & \alpha_1 & 0.769^{***} \\ \text{Asiático} & 1.180^{***} & \alpha_2 & 1.406^{***} \\ \text{Afroamericano} & 1.643^{***} & \alpha_3 & 12.089^{***} \\ \text{R^2 Máximo Rescalado} & 0.102 & \\ \hline \end{array} } \] Notas: Fuente: Pauly y Herring (2007). \(^{***}\) indica que los \(p\)-valores asociados son menores a 0.01. Para la raza, Caucásico es la variable omitida.
Para interpretar las razones de probabilidades en Tabla 11.10, primero notamos que las estimaciones de los puntos de corte, correspondientes a \(\alpha_1,\) \(\alpha_2\) y \(\alpha_3\), aumentan a medida que las opciones se vuelven menos restrictivas, como se anticipaba. Para el género, vemos que las probabilidades estimadas para las mujeres son 1.064 veces las de los hombres en la dirección de elegir un plan de salud menos restrictivo. Controlando por otras variables, las mujeres tienen más probabilidades de elegir planes menos restrictivos que los hombres. De manera similar, los más jóvenes, menos adinerados, no caucásicos y fumadores tienen más probabilidades de elegir planes menos restrictivos. Los coeficientes asociados con el tamaño de la familia, educación, toma de riesgos y salud auto-reportada no fueron estadísticamente significativos en este modelo ajustado.
11.6.2 Probit Acumulativo
Como en la Sección 11.2.2 para la regresión logística, los modelos de logit acumulativo tienen una interpretación de umbral. Específicamente, sea \(y_i^{\ast}\) una variable latente, no observada, aleatoria sobre la cual basamos la variable dependiente observada como \[ y_i=\left\{ \begin{array}{cc} 1 & y_i^{\ast} \le \alpha_1 \\ 2 & \alpha_1 < y_i^{\ast} \le \alpha_2 \\ \vdots & \vdots \\ c-1 & \alpha_{c-2} < y_i^{\ast} \le \alpha_{c-1} \\ c & \alpha_{c-1} < y_i^{\ast}\\ \end{array} \right. . \] Si \(y_i^{\ast} - \mathbf{x}_i^{\prime}\boldsymbol \beta\) tiene una distribución logística, entonces \[ \Pr(y_i^{\ast} - \mathbf{x}_i^{\prime}\boldsymbol \beta \le a)=\frac{1}{1+\exp (-a)} \] y por lo tanto \[ \Pr(y_i \le j ) = \Pr(y_i^{\ast} \le \alpha_j) =\frac{1}{1+\exp \left( -(\alpha_j - \mathbf{x}_i^{\prime}\boldsymbol \beta) \right)}. \] Aplicando la transformación logit a ambos lados se obtiene la ecuación (11.12).
Alternativamente, asumamos que \(y_i^{\ast} - \mathbf{x}_i^{prime}\boldsymbol \beta\) tiene una distribución normal estándar. Entonces, \[ \Pr(y_i \le j ) = \Pr(y_i^{\ast} \le \alpha_j) =\Phi \left( \alpha_j - \mathbf{x}_i^{\prime}\boldsymbol \beta \right). \] Este es el modelo de probit acumulativo. Al igual que en los modelos de variables binarias, el probit acumulativo da resultados que son similares al modelo logit acumulativo.
11.7 Lecturas Adicionales y Referencias
Los modelos de regresión de variables binarias se utilizan ampliamente. Para introducciones más detalladas, consulte Hosmer y Lemshow (1989) o Agresti (1996). También puede examinar tratamientos más rigurosos como los de Agresti (1990) y Cameron y Trivedi (1998). El trabajo de Agresti (1990, 1996) discute variables dependientes multicategoría, al igual que el tratamiento avanzado de econometría en Amemiya (1985).
Referencias del Capítulo
- Agresti, Alan (1990). Categorical Data Analysis. Wiley, New York.
- Agresti, Alan (1996). An Introduction to Categorical Data Analysis. Wiley, New York.
- Amemiya, Takeshi (1985). Advanced Econometrics. Harvard University Press, Cambridge, Massachusetts.
- Browne, Mark J. and Edward W. Frees (2007). Prohibitions on health insurance underwriting. Working paper.
- Cameron, A. Colin and Pravin K. Trivedi (1998). Regression Analysis of Count Data. Cambridge University Press, Cambridge.
- Carroll, Raymond J. and David Ruppert (1988). Transformation and Weighting in Regression. Chapman-Hall.
- Gourieroux, Christian and Joann Jasiak (2007). The Econometrics of Individual Risk. Princeton University Press, Princeton.
- Hand, D.J. and W. E. Henley (1997). Statistical classification methods in consumer credit scoring: A review. Journal of the Royal Statistical Society A, 160(3), 523-541.
- Hosmer, David W. and Stanley Lemeshow (1989). Applied Logistic Regression. Wiley, New York.
- Pauly, Mark V. and Bradley Herring (2007). The demand for health insurance in the group setting: Can you always get what you want? Journal of Risk and Insurance 74, 115-140.
- Smith, Richard M. and Phyllis Schumacher (2006). Academic attributes of college freshmen that lead to success in actuarial studies in a business college. Journal of Education for Business 81(5), 256-260.
- Valletta, R. G. (1999). Declining job security. Journal of Labor Economics 17, S170-S197.
- Wiginton, John C. (1980). A note on the comparison of logit and discriminant models of consumer credit behavior. Journal of Financial and Quantitative Analysis 15(3), 757-770.
11.8 Ejercicios
11.1 Similitud entre Logit y Probit. Suponga que la variable aleatoria \(y^{\ast}\) tiene una función de distribución logit, \(\Pr(y^{\ast} le y) = \mathrm{F}(y) = e^y/(1+e^y).\)
Calcule la correspondiente función de densidad de probabilidad.
Utilice la función de densidad de probabilidad para calcular la media (\(\mu_y\)).
Calcule la desviación estándar correspondiente (\(\sigma_y\)).
Defina la variable aleatoria reescalada \(y^{\ast \ast} =\frac{y^{\ast}-\mu_y}{\sigma_y}.\) Determine la función de densidad de probabilidad para \(y^{\ast \ast}\).
Trace la función de densidad de probabilidad en la parte (d). Superponga este gráfico con uno de una función de densidad de probabilidad normal estándar. (Esto proporciona una versión de la función de densidad de las gráficas de la función de distribución en la Figura 11.1.)
11.2 Interpretación de umbral del modelo de regresión probit. Considere un modelo lineal subyacente, \(y_i^{\ast }=\mathbf{x}_i^{\mathbf{ \prime }}\boldsymbol \beta+\epsilon_i^{\ast }\), donde \(\epsilon_i^{\ast }\) está distribuido normalmente con media cero y varianza \(\sigma ^{2}\). Defina \(y_i=\mathrm{I}(y_i^{\ast }>0),\) donde I(\(\cdot\)) es la función indicadora. Muestre que \(\pi_i=\Pr (y_i=1|\mathbf{x}_i)\) \(=\mathrm{\Phi }(\mathbf{x}_i^{\mathbf{\prime }}\mathbf{\beta /\sigma })\), donde \(\mathrm{\Phi }(\cdot)\) es la función de distribución normal estándar.
11.3 Interpretación de utilidad aleatoria del modelo de regresión logística. Bajo la interpretación de utilidad aleatoria, un individuo con utilidad $ U_{ij}=u_i(V_{ij}+_{ij})$, donde \(j\) puede ser 1 o 2, selecciona la categoría correspondiente a \(j=1\) con probabilidad \[\begin{eqnarray*} \pi_i &=& \Pr (y_i =1)=\mathrm{\Pr }(U_{i2}<U_{i1}) \\ &=&\mathrm{\Pr }(\epsilon _{i2}-\epsilon _{i1}<V_{i1}-V_{i2}). \end{eqnarray*}\] Como en la Sección 11.2.3, tomamos \(V_{i2}=0\) y \(V_{i1}=\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta\). Supongamos además que los errores provienen de una distribución de valor extremo de la forma \[ \Pr (\epsilon_{ij}<a)=\exp (-e^{-a}). \] Muestre que la probabilidad de elección \(\pi_i\) tiene una forma logit. Es decir, muestre que \[ \pi_i=\frac{1}{1+\exp (-\mathbf{x}_i^{\mathbf{\prime }}\boldsymbol \beta)}. \]
11.4 Dos Poblaciones.
Comience con una población y suponga que \(y_1, \ldots, y_n\) es una muestra i.i.d. de una distribución Bernoulli con media \(\pi\). Muestre que el estimador de máxima verosimilitud de \(\pi\) es \(\overline{y}\).
Ahora considere dos poblaciones. Suponga que \(y_1, \ldots, y_{n_1}\) es una muestra i.i.d. de una distribución Bernoulli con media \(\pi_1\) y que \(y_{n_1+1}, \ldots, y_{n_1+n_2}\) es una muestra i.i.d. de una distribución Bernoulli con media \(\pi_2\), donde las muestras son independientes entre sí.
b(i). Muestre que el estimador de máxima verosimilitud de \(\pi_2 - \pi_1\) es \(\overline{y}_2 - \overline{y}_1\).
b(ii). Determine la varianza del estimador en la parte b(i).
Ahora exprese el problema de las dos poblaciones en un contexto de regresión usando una variable explicativa. Específicamente, suponga que \(x_i\) solo toma los valores 0 y 1. De las \(n\) observaciones, \(n_1\) toman el valor \(x=0\). Estas \(n_1\) observaciones tienen un valor promedio de \(y\) de \(\overline{y}_1\). Las restantes \(n_2 =n-n_1\) observaciones tienen el valor \(x=1\) y un valor promedio de \(y\) de \(\overline{y}_2\). Usando el caso logit, sea \(b_{0,MLE}\) y \(b_{1,MLE}\) representen los estimadores de máxima verosimilitud de \(\beta_0\) y \(\beta_1\), respectivamente.
c(i). Muestre que los estimadores de máxima verosimilitud satisfacen las ecuaciones \[ \overline{y}_1 = \mathrm{\pi}\left(b_{0,MLE}\right) \] y \[ \overline{y}_2 = \mathrm{\pi}\left(b_{0,MLE}+b_{1,MLE}\right). \]
c(ii). Use la parte c(i) para mostrar que el estimador de máxima verosimilitud para \(\beta_1\) es \(\mathrm{\pi}^{-1}(\overline{y}_2)-\mathrm{\pi}^{-1}(\overline{y}_1)\).
c(iii). Con la notación \(\pi_1 = \mathrm{\pi}(\beta_0)\) y \(\pi_2 = \mathrm{\pi}(\beta_0 +\beta_1)\), confirme que la matriz de información se puede expresar como \[ \mathbf{I}(\beta_0, \beta_1) = n_1 \pi_1 (1-\pi_1) \left( \begin{array}{cc} 1 & 0 \\ 0 & 0 \\ \end{array} \right) + n_2 \pi_2 (1-\pi_2) \left( \begin{array}{cc} 1 & 1 \\ 1 & 1 \\ \end{array} \right). \]
c(iv). Utilice la matriz de información para determinar la varianza en muestras grandes del estimador de máxima verosimilitud para \(\beta_1\).
11.5 Valores Ajustados. Sea \(\widehat{y}_i = \mathrm{\pi }\left( \mathbf{x}_i^{\prime} \mathbf{b}_{MLE})\right)\) el \(i\)-ésimo valor ajustado para la función logit. Suponga que se utiliza un intercepto en el modelo, de modo que una de las variables explicativas \(x\) es una constante igual a uno. Muestre que la respuesta promedio es igual al valor ajustado promedio, es decir, muestre que \(\overline{y} = n^{-1} \sum_{i=1}^n \widehat{y}_i\).
11.6 Comenzando con las ecuaciones de puntaje (11.4), verifique la expresión para el caso logit en la ecuación (11.5).
11.7 Matriz de Información
Comenzando con la función de puntaje para el caso logit en la ecuación (11.5), muestre que la matriz de información puede ser expresada como \[ \mathbf{I}(\boldsymbol \beta) = \sum\limits_{i=1}^{n} \sigma_i^2 \mathbf{x}_i\mathbf{x}_i^{\mathbf{\prime }}, \] donde \(\sigma_i^2 = \mathrm{\pi}(\mathbf{x}_i^{\prime} \boldsymbol \beta)(1-\mathrm{\pi}(\mathbf{x}_i^{\prime}\boldsymbol \beta))\).
Comenzando con la función de puntaje general en la ecuación (11.4), determine la matriz de información.
11.8 Reclamaciones de seguro por lesiones en automóviles. Refiérase a la descripción en el Ejercicio 1.5.
Consideramos \(n=1,340\) reclamaciones por responsabilidad civil por lesiones corporales de un solo estado utilizando una encuesta de 2002 realizada por el Consejo de Investigación de Seguros (IRC). El IRC es una división del Instituto Americano de Chartered Property Casualty Underwriters y el Instituto de Seguros de América. La encuesta solicitó a las empresas participantes que informaran sobre reclamaciones cerradas con pago durante un período de dos semanas designado. En esta asignación, nos interesa entender las características de los demandantes que eligen ser representados por un abogado al resolver su reclamo. Las descripciones de las variables se dan en la Tabla 11.11.
| Variable | \(\textbf{Descripción}\) |
|---|---|
| ATTORNEY | si el reclamante está representado por un abogado (=1 si sí y =2 si no) |
| CLMAGE | edad del reclamante |
| CLMSEX | género del reclamante (=1 si masculino y =2 si femenino) |
| MARITAL | estado civil del reclamante (=1 si casado, =2 si soltero, =3 si viudo, y =4 si divorciado/separado) |
| SEATBELT | si el reclamante estaba usando un cinturón de seguridad/restricción infantil (=1 si sí, =2 si no, y =3 si no aplicable) |
| CLMINSUR | si el conductor del vehículo del reclamante estaba sin seguro (=1 si sí, =2 si no, y =3 si no aplicable) |
| LOSS | pérdida económica total del reclamante (en miles). |
Estadísticas Resumidas.
Calcule histogramas y estadísticas resumidas de las variables explicativas continuas CLMAGE y LOSS. Basado en estos resultados, cree una versión logarítmica de LOSS, llamada lnLOSS.
Examine las medias de CLMAGE, LOSS y lnLOSS por nivel de ATTORNEY. ¿Sugieren estas estadísticas que las variables continuas difieren según ATTORNEY?
Cree tablas de conteo (o porcentajes) de ATTORNEY por nivel de CLMSEX, MARITAL, SEATBELT y CLMINSUR. ¿Sugieren estas estadísticas que las variables categóricas difieren según ATTORNEY?
Identifique el número de valores faltantes para cada variable explicativa.
Modelos de Regresión Logística.
Ejecute un modelo de regresión logística utilizando solo la variable explicativa CLMSEX. ¿Es un factor importante para determinar el uso de un abogado? Proporcione una interpretación en términos de las probabilidades de usar un abogado.
Ejecute un modelo de regresión logística utilizando las variables explicativas CLMAGE, CLMSEX, MARITAL, SEATBELT y CLMINSUR. ¿Qué variables parecen ser estadísticamente significativas?
Para el modelo en la parte (ii), ¿quién usa más abogados, hombres o mujeres? Proporcione una interpretación en términos de las probabilidades de usar un abogado para la variable CLMSEX.
Ejecute un modelo de regresión logística utilizando las variables explicativas CLMAGE, CLMSEX, MARITAL, SEATBELT, CLMINSUR, LOSS y lnLOSS. Decida cuál de las dos medidas de pérdida es más importante y vuelva a ejecutar el modelo utilizando solo una de estas variables. En este modelo, ¿es la medida de las pérdidas una variable estadísticamente significativa?
Ejecute su modelo en la parte (iv) pero omitiendo la variable CLMAGE. Describa las diferencias entre este ajuste de modelo y el de la parte (iv), enfocándose en las variables estadísticamente significativas y en el número de observaciones utilizadas en el ajuste del modelo.
Considere un reclamante masculino soltero de 32 años de edad. Suponga que el reclamante estaba usando un cinturón de seguridad, que el conductor estaba asegurado y la pérdida económica total es de $5,000. Para el modelo en la parte (iv), ¿cuál es la estimación de la probabilidad de usar un abogado?
Regresión Probit. Repita la parte b(v) utilizando modelos de regresión probit, pero interprete solo el signo de los coeficientes de regresión.
11.9 Carreras de Caballos en Hong Kong. El hipódromo es un ejemplo fascinante de la dinámica de los mercados financieros en acción. Vamos a la pista y hagamos una apuesta. Supongamos que, de un campo de 10 caballos, simplemente queremos elegir un ganador. En el contexto de la regresión, dejaremos que \(y\) sea la variable de respuesta que indica si un caballo gana (\(y\) = 1) o no (\(y\) = 0). De los formularios de carreras, periódicos, y otras fuentes, hay muchas variables explicativas que están disponibles públicamente y que podrían ayudarnos a predecir el resultado para \(y\). Algunas variables candidatas pueden incluir la edad del caballo, el rendimiento reciente del caballo y el jinete, el pedigrí del caballo, y así sucesivamente. Estas variables son evaluadas por los inversores presentes en la carrera, la multitud apostadora. Al igual que en muchos mercados financieros, resulta que una de las variables explicativas más útiles es la evaluación general de la multitud sobre las habilidades del caballo. Estas evaluaciones no se hacen basadas en una encuesta de la multitud, sino más bien en función de las apuestas realizadas. La información sobre las apuestas de la multitud está disponible en un gran cartel en la carrera llamado el tote board (tablero de apuestas). El tote board muestra las probabilidades de que cada caballo gane una carrera. Tabla 11.12 es un tote board hipotético para una carrera de 10 caballos.
Tabla 11.12. Tote Board Hipotético
\[ \scriptsize{ \begin{array}{l|cccccccccc} \hline \text{Caballo} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \text{Probabilidades Publicadas} & 1-1 & 79-1 & 7-1 & 3-1 & 15-1 & 7-1 & 49-1 & 49-1 & 19-1 & 79-1 \\ \hline \end{array} } \]
Las probabilidades que aparecen en el tote board han sido ajustadas para proporcionar una “tasa de la pista.” Es decir, por cada dólar apostado, $\(T\) va a la pista por patrocinar la carrera y $(1-\(T\)) va a los apostadores ganadores. Las tasas típicas de la pista están en el orden del veinte por ciento, o \(T\)=0.20.
Podemos convertir fácilmente las probabilidades en el tote board en la evaluación de la multitud de las probabilidades de ganar. Para ilustrar esto, Tabla 11.13 muestra apuestas hipotéticas para ganar que resultaron en la información mostrada en el tote board hipotético en la Tabla 11.12.
Tabla 11.13. Apuestas Hipotéticas
\[ \scriptsize{ \begin{array}{l|cccccccccc} \hline \text{Caballo} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & Total\\ \hline \text{Apuestas para Ganar} & 8,000 & 200 & 2,000 & 4,000 & 1,000 & 3,000 & 400 & 400 & 800 & 200 & 20,000 \\ \text{Probabilidad} & 0.40 & 0.01 & 0.10 & 0.20 & 0.05 & 0.15 & 0.02 & 0.02 & 0.04 & 0.02 & 1.000 \\ \text{Probabilidades Publicadas} & 1-1 & 79-1 & 7-1 & 3-1 & 15-1 & 7-1 & 49-1 & 49-1 & 19-1 & 79-1 \\ \hline \end{array} } \]
Para esta carrera hipotética, se apostaron 20,000 para ganar. Debido a que 8,000 de estos 20,000 se apostaron en el primer caballo, interprete la relación 8000/20000 = 0.40 como la evaluación de la multitud de la probabilidad de ganar. Las probabilidades teóricas se calculan como 0.4/(1-0.4) = 2/3, o una apuesta de 0.67 gana 1. Sin embargo, las probabilidades teóricas asumen un juego justo sin tasa de la pista. Para ajustar al hecho de que solo (1-\(T\)) están disponibles para el ganador, las probabilidades publicadas para este caballo serían 0.4/(1-\(T\)-0.4) = 1, si \(T\)=0.20. En este caso, ahora se requiere una apuesta de 1 para ganar 1. Entonces tenemos la relación \(probabilidades~ajustadas\) \(= x/(1-T-x)\), donde \(x\) es la evaluación de la multitud de la probabilidad de ganar.
Antes del inicio de la carrera, el tote board nos proporciona probabilidades ajustadas que pueden convertirse fácilmente en \(x\), la evaluación de la multitud sobre ganar. Usamos esta medida para ayudarnos a predecir \(y\), el evento de que el caballo realmente gane la carrera.
Consideramos datos de 925 carreras realizadas en Hong Kong desde septiembre de 1981 hasta septiembre de 1989. En cada carrera, había diez caballos, uno de los cuales fue seleccionado aleatoriamente para estar en la muestra. En los datos, use FINISH = \(y\) como el indicador de que un caballo gane una carrera y WIN = \(x\) como la evaluación a priori de la multitud de la probabilidad de que un caballo gane una carrera.
Un colega estadísticamente ingenuo quisiera duplicar el tamaño de la muestra eligiendo dos caballos de cada carrera en lugar de seleccionar aleatoriamente un caballo de un campo de 10.
Describa la relación entre las variables dependientes de los dos caballos seleccionados.
Explique cómo esto viola las suposiciones del modelo de regresión.
Calcule la media de FINISH y las estadísticas resumidas de WIN. Note que la desviación estándar de FINISH es mayor que la de WIN, aunque las medias de las muestras sean aproximadamente las mismas. Para la variable FINISH, ¿cuál es la relación entre la media muestral y la desviación estándar?
Calcule las estadísticas resumidas de WIN por nivel de FINISH. Note que la media muestral es mayor para los caballos que ganaron (FINISH = 1) que para aquellos que perdieron (FINISH = 0). Interprete este resultado.
Estime un modelo de probabilidad lineal, utilizando WIN para predecir FINISH.
¿Es WIN un predictor estadísticamente significativo de FINISH?
¿Qué tan bien se ajusta este modelo a los datos utilizando la estadística de bondad de ajuste habitual?
Para este modelo estimado, ¿es posible que los valores ajustados se encuentren fuera del intervalo [0, 1]? Note que, por definición, la variable x WIN debe estar dentro del intervalo [0, 1].
Estime un modelo de regresión logística, utilizando WIN para predecir FINISH. ¿Es WIN un predictor estadísticamente significativo de FINISH?
Compare los valores ajustados de los modelos en las partes (d) y (e)
Para cada modelo, proporcione valores ajustados en WIN = 0, 0.01, 0.05, 0.10 y 1.0.
Trace un gráfico de los valores ajustados del modelo de probabilidad lineal versus los valores ajustados del modelo de regresión logística.
Interprete WIN como la evaluación a priori de la multitud de la probabilidad de que un caballo gane una carrera. Los valores ajustados, FINISH, es su nueva estimación de la probabilidad de que un caballo gane una carrera, basada en la evaluación de la multitud.
Trace el gráfico de la diferencia FINISH - WIN versus WIN.
Discuta una estrategia de apuestas que podría emplear basada en la diferencia, FINISH - WIN.
11.10 Demanda de Seguro de Vida a Término. Continuamos nuestro estudio de la Demanda de Seguro de Vida a Término de los Capítulos 3 y 4. Específicamente, examinamos la Encuesta de Finanzas del Consumidor (SCF) de 2004, una muestra representativa a nivel nacional que contiene información extensa sobre activos, pasivos, ingresos y características demográficas de los encuestados (potenciales clientes de EE. UU.). Ahora volvemos a la muestra original de \(n=500\) familias con ingresos positivos y estudiamos si una familia compra o no seguro de vida a término. De nuestra muestra, resulta que 225 no compraron (FACEPOS=0), mientras que 275 sí compraron seguro de vida a término (FACEPOS=1).
Estadísticas Resumidas. Proporcione una tabla de medias de las variables explicativas por nivel de la variable dependiente FACEPOS. Interprete lo que aprendemos de esta tabla.
Modelo de Probabilidad Lineal. Ajuste un modelo de probabilidad lineal usando FACEPOS como la variable dependiente y LINCOME, EDUCATION, AGE y GENDER como variables explicativas continuas, junto con el factor MARSTAT.
b(i). Defina brevemente un modelo de probabilidad lineal.
b(ii). Comente sobre la calidad del modelo ajustado.
b(iii). ¿Cuáles son los tres principales inconvenientes del modelo de probabilidad lineal?
Modelo de Regresión Logística. Ajuste un modelo de regresión logística utilizando el mismo conjunto de variables explicativas.
c(i). Identifique qué variables parecen ser estadísticamente significativas. En su identificación, describa la base para sus conclusiones.
c(ii). ¿Qué medida resume la bondad de ajuste?
Modelo de Regresión Logística Reducido. Defina MARSTAT1 como una variable binaria que indica MARSTAT=1. Ajuste un segundo modelo de regresión logística utilizando LINCOME, EDUCATION y MARSTAT1.
d(i). Compare estos dos modelos, utilizando una prueba de razón de verosimilitud. Establezca sus hipótesis nula y alternativa, criterio de decisión y su regla de decisión.
d(ii). ¿Quién es más probable que compre un seguro de vida a término, casados o no casados? Proporcione una interpretación en términos de las probabilidades de comprar un seguro de vida a término para la variable MARSTAT1.
d(iii). Considere a un hombre casado que tiene 54 años. Suponga que esta persona tiene 13 años de educación, un salario anual de $70,000 y vive en un hogar compuesto por cuatro personas. Para este modelo, ¿cuál es la estimación de la probabilidad de comprar un seguro de vida a término?
11.11 Éxito en los Estudios Actuariales. Al igual que en los campos médicos y legales, los miembros de la profesión actuarial enfrentan problemas interesantes y generalmente son bien remunerados por sus esfuerzos en resolver estos problemas. También, como en las profesiones médicas y legales, las barreras educativas para convertirse en actuario son desafiantes, limitando la entrada en el campo.
Para asesorar a los estudiantes sobre si tienen el potencial para cumplir con las demandas de este campo intelectualmente desafiante, Smith y Schumacher (2006) estudiaron los atributos de los estudiantes en una facultad de negocios. Específicamente, examinaron a \(n=185\) estudiantes de primer año en la Universidad de Bryant en Rhode Island que habían comenzado sus carreras universitarias entre 1995 y 2001. La variable dependiente de interés era si se graduaron con una concentración en actuaría, para estos estudiantes el primer paso para convertirse en actuario profesional. De estos, 77 se graduaron con una concentración en actuaría y los otros 108 abandonaron la concentración (en Bryant, la mayoría se transfirió a otras concentraciones, aunque algunos dejaron la universidad).
Smith y Schumacher (2006) informaron sobre los efectos de cuatro mecanismos de evaluación temprana, así como GENDER, una variable de control. Los mecanismos de evaluación fueron: PLACE%, rendimiento en un examen de ubicación matemática administrado justo antes del primer año, MSAT y VSAT, las porciones de matemáticas (M) y verbal (V) del Scholastic Aptitude Test (SAT), y RANK, el rango en la escuela secundaria dado como una proporción (siendo más cercano a uno mejor). La Tabla 11.14 muestra que los estudiantes que eventualmente se graduaron con una concentración en actuaría obtuvieron mejores resultados en estos mecanismos de evaluación temprana que los que abandonaron la concentración actuarial.
Se ajustó una regresión logística a los datos, con los resultados reportados en la Tabla 11.14.
Para tener una idea de qué variables son estadísticamente significativas, calcule los \(t\)-ratios para cada variable. Para cada variable, indique si es o no estadísticamente significativa.
Para tener una idea del impacto relativo de los mecanismos de evaluación, use los coeficientes en la Tabla 11.14 para calcular las probabilidades de éxito estimadas para las siguientes combinaciones de variables. En sus cálculos, asuma que GENDER=1.
b(i). Asuma PLACE% =0.80, MSAT = 680, VSAT=570 y RANK=0.90.
b(ii). Asuma PLACE% =0.60, MSAT = 680, VSAT=570 y RANK=0.90.
b(iii). Asuma PLACE% =0.80, MSAT = 620, VSAT=570 y RANK=0.90.
b(iv). Asuma PLACE% =0.80, MSAT = 680, VSAT=540 y RANK=0.90.
b(v). Asuma PLACE% =0.80, MSAT = 680, VSAT=570 y RANK=0.70.
|
Promedio para Actuariales
|
Regresión Logística
|
|||
|---|---|---|---|---|
| Variable | Graduados | Desertores | Estimación | Error Estándar |
| Intercepto |
|
|
-12.094 | 2.575 |
| GENDER |
|
|
0.256 | 0.407 |
| PLACE% | 0.83 | 0.64 | 4.336 | 1.657 |
| MSAT | 679.25 | 624.25 | 0.008 | 0.004 |
| VSAT | 572.2 | 544.25 | -0.002 | 0.003 |
| RANK | 0.88 | 0.76 | 4.442 | 1.836 |
11.12 Caso-Control. Considere el siguiente método de selección de muestra “caso-control” para variables dependientes binarias. Intuitivamente, si estamos trabajando con un problema donde el evento de interés es raro, queremos asegurarnos de que muestreamos una cantidad suficiente de eventos para que nuestros procedimientos de estimación sean confiables.
Suponga que tenemos una gran base de datos que consiste en \(\{y_i, \mathbf{x}_i\}\), con \(i=1,\ldots, N\) observaciones. (Para los registros de una compañía de seguros, \(N\) podría fácilmente ser de diez millones o más). Queremos asegurarnos de obtener una cantidad suficiente de \(y_i = 1\) (correspondiente a reclamaciones o “casos”) en nuestra muestra, más una muestra de \(y_i = 0\) (correspondiente a no reclamaciones o “controles”). Por lo tanto, dividimos el conjunto de datos en dos subconjuntos. Para el primer subconjunto que consiste en observaciones con \(y_i = 1\), tomamos una muestra aleatoria con probabilidad \(\tau_1\). De manera similar, para el segundo subconjunto que consiste en observaciones con \(y_i = 0\), tomamos una muestra aleatoria con probabilidad \(\tau_0\). Por ejemplo, en la práctica podríamos usar \(\tau_1=1\) y \(\tau_0 = 0.10\), lo que correspondería a tomar todas las reclamaciones y una muestra del 10% de no reclamaciones - por lo tanto, se considera que \(\tau_1\) y \(\tau_0\) son conocidos por el analista.
Sea \(\{r_i = 1\}\) el evento que indica que la observación es seleccionada para ser parte del análisis. Determine \(\Pr(y_i = 1, r_i = 1)\), \(\Pr(y_i = 0, r_i = 1)\) y \(\Pr(r_i = 1)\) en términos de \(\tau_0\), \(\tau_1\) y \(\pi_i = \Pr(y_i=1)\).
Usando los cálculos en la parte (a), determine la probabilidad condicional \(\Pr(y_i=1 | r_i=1)\).
Ahora suponga que \(\pi_i\) tiene una forma logística (\(\pi(z) = \exp(z)/(1+\exp(z))\) y \(\pi_i= \pi(\mathbf{x}_i^{\prime}\boldsymbol \beta ))\). Reescriba su respuesta a la parte (b) usando esta forma logística.
Escriba la verosimilitud de los \(y_i\) observados (condicional en \(r_i = 1, i=1, \ldots, n\)). Muestre cómo podemos interpretar esto como la verosimilitud de una regresión logística usual con la excepción de que el intercepto ha cambiado. Especifique el nuevo intercepto en términos del intercepto original, \(\tau_0\) y \(\tau_1\).
11.9 Suplementos Técnicos - Inferencia Basada en Verosimilitud
Comencemos con variables aleatorias \(\left( y_1, \ldots, y_n \right) ^{\prime} = \mathbf y\) cuya distribución conjunta es conocida hasta un vector de parámetros \(\boldsymbol \theta\). En aplicaciones de regresión, \(\boldsymbol \theta\) consiste en los coeficientes de regresión, \(\boldsymbol \beta\), y posiblemente un parámetro de escala \(\sigma^2\) así como parámetros adicionales. Esta función de densidad de probabilidad conjunta se denota como \(\mathrm{f}(\mathbf{y};\boldsymbol \theta)\). La función también puede ser una función de masa de probabilidad para variables aleatorias discretas o una distribución mixta para variables aleatorias que tienen componentes discretos y continuos. En cada caso, podemos usar la misma notación, \(\mathrm{f}(\mathbf{y};\boldsymbol \theta),\) y llamarla la función de verosimilitud. La verosimilitud es una función de los parámetros con los datos (\(\mathbf{y}\)) fijos en lugar de una función de los datos con los parámetros (\(\boldsymbol \theta\)) fijos.
Es habitual trabajar con la versión logarítmica de la función de verosimilitud y así definimos la función de log-verosimilitud como \[ L(\boldsymbol \theta) = L(\mathbf{y};\boldsymbol \theta ) = \ln \mathrm{f}(\mathbf{y};\boldsymbol \theta), \] evaluada en una realización de \(\mathbf{y}\). En parte, esto se debe a que a menudo trabajamos con el caso especial importante donde las variables aleatorias \(y_1, \ldots, y_n\) son independientes. En este caso, la función de densidad conjunta se puede expresar como un producto de las funciones de densidad marginales y, al tomar logaritmos, podemos trabajar con sumas. Incluso cuando no se trata de variables aleatorias independientes, como con datos de series temporales, a menudo es más conveniente desde el punto de vista computacional trabajar con log-verosimilitudes en lugar de la función de verosimilitud original.
11.9.1 Propiedades de las Funciones de Verosimilitud
Dos propiedades básicas de las funciones de verosimilitud son: \[\begin{equation} \mathrm{E} \left( \frac{ \partial}{\partial \boldsymbol \theta} L(\boldsymbol \theta) \right) = \mathbf 0 \tag{11.13} \end{equation}\] y \[\begin{equation} \mathrm{E} \left( \frac{ \partial^2}{\partial \boldsymbol \theta \partial \boldsymbol \theta^{\prime}} L(\boldsymbol \theta) \right) + \mathrm{E} \left( \frac{ \partial L(\boldsymbol \theta)}{\partial \boldsymbol \theta} \frac{ \partial L(\boldsymbol \theta)}{\partial \boldsymbol \theta^{\prime}} \right) = \mathbf 0. \tag{11.14} \end{equation}\]
La derivada de la función de log-verosimilitud, \(\partial L(\boldsymbol \theta)/\partial \boldsymbol \theta\), se llama función de puntaje. La ecuación (11.13) muestra que la función de puntaje tiene media cero. Para ver esto, bajo condiciones de regularidad adecuadas, tenemos \[\begin{eqnarray*} \mathrm{E} \left( \frac{ \partial}{\partial \boldsymbol \theta} L(\boldsymbol \theta) \right) &=& \mathrm{E} \left( \frac{ \frac{\partial}{\partial \boldsymbol \theta} \mathrm{f}(\mathbf{y};\boldsymbol \theta )}{\mathrm{f}(\mathbf{y};\boldsymbol \theta )} \right) = \int \frac{\partial}{\partial \boldsymbol \theta} \mathrm{f}(\mathbf{y};\boldsymbol \theta ) d \mathbf y = \frac{\partial}{\partial \boldsymbol \theta} \int \mathrm{f}(\mathbf{y};\boldsymbol \theta ) d \mathbf y \\ &=& \frac{\partial}{\partial \boldsymbol \theta} 1 = \mathbf 0. \end{eqnarray*}\] Por conveniencia, esta demostración asume una densidad para f(\(\cdot\)); las extensiones a distribuciones de masa y mixtas son sencillas. La demostración de la ecuación (11.14) es similar y se omite. Para establecer la ecuación (11.13), implícitamente utilizamos “condiciones de regularidad adecuadas” para permitir el intercambio de la derivada y el signo de integral. Para ser más precisos, un analista que trabaje con un tipo específico de distribución puede utilizar esta información para verificar que el intercambio de la derivada y el signo de integral es válido.
Usando la ecuación (11.14), podemos definir la matriz de información \[\begin{equation} \mathbf{I}(\boldsymbol \theta) = \mathrm{E} \left( \frac{ \partial L(\boldsymbol \theta)}{\partial \boldsymbol \theta} \frac{ \partial L(\boldsymbol \theta)}{\partial \boldsymbol \theta^{\prime}} \right) = -\mathrm{E} \left( \frac{ \partial^2}{\partial \boldsymbol \theta \partial \boldsymbol \theta^{\prime}} L(\boldsymbol \theta) \right). \tag{11.15} \end{equation}\] Esta cantidad se utiliza ampliamente en el estudio de las propiedades de muestras grandes de las funciones de verosimilitud.
La matriz de información aparece en la distribución de muestras grandes de la función de puntaje. Específicamente, bajo condiciones amplias, tenemos que \(\partial L(\boldsymbol \theta)/\partial \boldsymbol \theta\) tiene una distribución normal en muestras grandes con media 0 y varianza \(\mathbf{I}(\boldsymbol \theta)\). Para ilustrar, supongamos que las variables aleatorias son independientes, de modo que la función de puntaje se puede escribir como \[ \frac{ \partial}{\partial \boldsymbol \theta} L(\boldsymbol \theta) =\frac{ \partial}{\partial \boldsymbol \theta} \ln \prod_{i=1}^n \mathrm{f}(y_i;\boldsymbol \theta ) =\sum_{i=1}^n \frac{ \partial}{\partial \boldsymbol \theta} \ln \mathrm{f}(y_i;\boldsymbol \theta ). \] La función de puntaje es la suma de variables aleatorias con media cero debido a la ecuación (11.13); los teoremas del límite central están ampliamente disponibles para garantizar que las sumas de variables aleatorias independientes tengan distribuciones normales en muestras grandes (ver Sección 1.4 para un ejemplo). Además, si las variables aleatorias son idénticas, entonces a partir de la ecuación (11.15) podemos ver que el segundo momento de \(\partial \ln \mathrm{f}(y_i;\boldsymbol \theta ) /\partial \boldsymbol \theta\) es la matriz de información, obteniendo el resultado.
11.9.2 Estimadores de Máxima Verosimilitud
Los estimadores de máxima verosimilitud son valores de los parámetros \(\boldsymbol \theta\) que son “más probables” de haber sido producidos por los datos. El valor de \(\boldsymbol \theta\), denotado como \(\boldsymbol \theta_{MLE}\), que maximiza \(\mathrm{f}(\mathbf{y};\boldsymbol \theta)\) se llama el estimador de máxima verosimilitud. Debido a que \(\ln(\cdot)\) es una función uno a uno, también podemos determinar \(\boldsymbol \theta_{MLE}\) maximizando la función de log-verosimilitud, \(L(\boldsymbol \theta)\).
Bajo condiciones amplias, tenemos que \(\boldsymbol \theta_{MLE}\) tiene una distribución normal en muestras grandes con media \(\boldsymbol \theta\) y varianza \(\left( \mathbf{I}(\boldsymbol \theta) \right)^{-1}\). Este es un resultado crítico sobre el cual se basa gran parte de la estimación y la prueba de hipótesis. Para subrayar este resultado, examinamos el caso especial de la regresión “basada en normales”.
Caso Especial. Regresión con distribuciones normales. Supongamos que \(y_1, \ldots, y_n\) son independientes y están distribuidos normalmente, con media \(\mathrm{E~}y_i = \mu_i = \mathbf{x}_i^{\prime} \boldsymbol \beta\) y varianza \(\sigma^2\). Los parámetros se pueden resumir como \(\boldsymbol \theta = \left( \boldsymbol \beta^{\prime}, \sigma^2 \right)^{\prime}.\) Recordemos de la ecuación (1.1) que la función de densidad de probabilidad normal es \[ \mathrm{f}(y; \mu_i, \sigma^2)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left( -\frac{1}{2\sigma^2}\left( y-\mu_i \right)^2\right) . \] Con esto, los dos componentes de la función de puntaje son \[\begin{eqnarray*} \frac{ \partial}{\partial \boldsymbol \beta} L(\boldsymbol \theta) &=& \sum_{i=1}^n \frac{ \partial}{\partial \boldsymbol \beta} \ln \mathrm{f}(y_i; \mathbf{x}_i^{\prime} \boldsymbol \beta, \sigma^2) =-\frac{1}{2\sigma^2} \sum_{i=1}^n \frac{ \partial}{\partial \boldsymbol \beta} \left(y_i-\mathbf{x}_i^{\prime} \boldsymbol \beta \right)^2 \\ &=& -\frac{(-2)}{2 \sigma^2} \sum_{i=1}^n \left(y_i-\mathbf{x}_i^{\prime} \boldsymbol \beta \right) \mathbf{x}_i \end{eqnarray*}\] y \[\begin{eqnarray*} \frac{ \partial}{\partial \sigma^2} L(\boldsymbol \theta) &=& \sum_{i=1}^n \frac{ \partial}{\partial \sigma^2} \ln \mathrm{f}(y_i; \mathbf{x}_i^{\prime} \boldsymbol \beta, \sigma^2) = -\frac{n}{2 \sigma^2} + \frac {1}{2 \sigma ^4}\sum_{i=1}^n \left(y_i-\mathbf{x}_i^{\prime} \boldsymbol \beta \right)^2 . \end{eqnarray*}\] Igualando estas ecuaciones a cero y resolviendo se obtienen los estimadores de máxima verosimilitud \[ \boldsymbol \beta_{MLE} = \left(\sum_{i=1}^n \mathbf{x}_i \mathbf{x}_i^{\prime}\right)^{-1} \sum_{i=1}^n \mathbf{x}_i y_i = \mathbf{b} \] y \[ \sigma^2_{MLE} = \frac{1}{n} \sum_{i=1}^n \left( y_i - \mathbf{x}_i^{\prime} \mathbf{b} \right)^2 = \frac{n-(k+1)}{n} s^2. \] Así, el estimador de máxima verosimilitud de \(\boldsymbol \beta\) es igual al estimador habitual de mínimos cuadrados. El estimador de máxima verosimilitud de \(\sigma^2\) es un múltiplo escalar del estimador habitual de mínimos cuadrados. El estimador de mínimos cuadrados \(s^2\) es insesgado, mientras que \(\sigma^2_{MLE}\) es solo aproximadamente insesgado en muestras grandes.
La matriz de información es
\[ \mathbf{I}(\boldsymbol \theta) = -\mathrm{E~} \left( \begin{array}{cc} \frac{ \partial^2}{\partial \boldsymbol \beta ~\partial \boldsymbol \beta^{\prime}} L(\boldsymbol \theta) & \frac{ \partial^2}{\partial \boldsymbol \beta ~\partial \sigma^2} L(\boldsymbol \theta) \\ \frac{ \partial^2}{\partial \sigma^2 \partial \boldsymbol \beta^{\prime} } L(\boldsymbol \theta) & \frac{ \partial^2}{\partial \sigma^2 \partial \sigma^2} L(\boldsymbol \theta)\\ \end{array} \right)= \left( \begin{array}{cc} \frac{ 1}{\sigma^2} \sum_{i=1}^n \mathbf{x}_i \mathbf{x}_i^{\prime} & 0 \\ 0 & \frac{n}{2 \sigma^4}\\ \end{array} \right). \] Así, \(\boldsymbol \beta_{MLE} = \mathbf{b}\) tiene una distribución normal en muestras grandes con media \(\boldsymbol \beta\) y matriz de varianza-covarianza \(\sigma^2 \left(\sum_{i=1}^n \mathbf{x}_i \mathbf{x}_i^{\prime} \right)^{-1}\), como se vio anteriormente. Además, \(\sigma^2_{MLE}\) tiene una distribución normal en muestras grandes con media \(\sigma^2\) y varianza \(2 \sigma^4 /n.\)
La máxima verosimilitud es una técnica de estimación general que se puede aplicar en muchos contextos estadísticos, no solo en aplicaciones de regresión y series temporales. Se puede aplicar ampliamente y disfruta de ciertas propiedades de optimalidad. Ya hemos mencionado el resultado de que los estimadores de máxima verosimilitud suelen tener una distribución normal en muestras grandes. Además, los estimadores de máxima verosimilitud son los más eficientes en el siguiente sentido. Supongamos que \(\widehat{\boldsymbol \theta}\) es un estimador alternativo insesgado. El teorema de Cramer-Rao establece, bajo condiciones de regularidad leves, para todos los vectores \(\mathbf c\), que \(\mathrm{Var~} \mathbf c^{\prime} \boldsymbol \theta_{MLE} \le \mathrm{Var~} \mathbf c^{\prime} \widehat{\boldsymbol \theta}\), para \(n\) suficientemente grande.
También notamos que \(2 \left( L(\boldsymbol \theta_{MLE}) - L(\boldsymbol \theta) \right)\) tiene una distribución chi-cuadrado con grados de libertad igual a la dimensión de \(\boldsymbol \theta\).
En algunas aplicaciones, como el caso de regresión con una distribución normal, los estimadores de máxima verosimilitud se pueden calcular analíticamente como una expresión de forma cerrada. Típicamente, esto se puede hacer encontrando raíces de la primera derivada de la función. Sin embargo, en general, los estimadores de máxima verosimilitud no se pueden calcular con expresiones de forma cerrada y se determinan iterativamente. Se utilizan ampliamente dos procedimientos generales: 1. Newton-Raphson utiliza el algoritmo iterativo \[\begin{equation} \boldsymbol \theta_{NEW} = \boldsymbol \theta_{OLD} - \left. \left\{ \left( \frac{ \partial^2 L}{\partial \boldsymbol \theta \partial \boldsymbol \theta^{\prime}} \right)^{-1} \frac{\partial L}{\partial \boldsymbol \theta } \right\} \right|_ {\boldsymbol \theta = \boldsymbol \theta_{OLD}} . \tag{11.16} \end{equation}\] 2. Puntuación de Fisher utiliza el algoritmo iterativo \[\begin{equation} \boldsymbol \theta_{NEW} = \boldsymbol \theta_{OLD} + \mathbf{I}(\boldsymbol \theta_{OLD})^{-1} \left. \left\{ \frac{\partial L}{\partial \boldsymbol \theta } \right\} \right|_ {\boldsymbol \theta = \boldsymbol \theta_{OLD}} . \tag{11.17} \end{equation}\] donde \(\mathbf{I}(\boldsymbol \theta)\) es la matriz de información.
11.9.3 Pruebas de Hipótesis
Consideramos probar la hipótesis nula \(H_0: h(\boldsymbol \theta) = \mathbf{d}\), donde \(\mathbf{d}\) es un vector conocido de dimensión \(r \times 1\) y h(\(\cdot\)) es conocido y diferenciable. Este marco de pruebas abarca como un caso especial la hipótesis lineal general introducida en el Capítulo 4.
Existen tres enfoques generales para probar hipótesis, denominados razón de verosimilitud, Wald y Rao. El enfoque de Wald evalúa una función de la verosimilitud en \(\boldsymbol \theta_{MLE}\). El enfoque de la razón de verosimilitud utiliza \(\boldsymbol \theta_{MLE}\) y \(\boldsymbol \theta_{Reduced}\). Aquí, \(\boldsymbol \theta_{Reduced}\) es el valor de \(\boldsymbol \theta\) que maximiza \(L(\boldsymbol \theta_{Reduced})\) bajo la restricción de que \(h(\boldsymbol \theta) = \mathbf{d}\). El enfoque de Rao también utiliza \(\boldsymbol \theta_{Reduced}\) pero lo determina maximizando \(L(\boldsymbol \theta) - \boldsymbol \lambda^{\prime}(h(\boldsymbol \theta) -\mathbf{d})\), donde \(\boldsymbol \lambda\) es un vector de multiplicadores de Lagrange. Por lo tanto, la prueba de Rao también se llama la prueba del multiplicador de Lagrange.
Las estadísticas de prueba asociadas con los tres enfoques son:
- \(LRT = 2 \times \left\{L(\boldsymbol \theta_{MLE})-L(\boldsymbol \theta_{Reduced}) \right\}\)
- Wald: \(TS_W(\boldsymbol \theta_{MLE})\), donde \[ TS_W(\boldsymbol \theta)=(h(\boldsymbol \theta) -\mathbf{d})^{\prime} \left\{ \frac{\partial}{\partial \boldsymbol \theta} h(\boldsymbol \theta)^{\prime} \left(-\mathbf{I}(\boldsymbol \theta) \right)^{-1} \frac{\partial}{\partial \boldsymbol \theta} h(\boldsymbol \theta) \right\}^{-1} (h(\boldsymbol \theta) -\mathbf{d}), \] y
- Rao: \(TS_R(\boldsymbol \theta_{Reduced})\), donde \[ TS_R(\boldsymbol \theta) = \frac{\partial}{\partial \boldsymbol \theta} L(\boldsymbol \theta) \left(-\mathbf{I}(\boldsymbol \theta) \right)^{-1} \frac{\partial}{\partial \boldsymbol \theta} L(\boldsymbol \theta)^{\prime}. \]
Bajo condiciones amplias, las tres estadísticas de prueba tienen distribuciones chi-cuadrado en muestras grandes con \(r\) grados de libertad bajo \(H_0\). Los tres métodos funcionan bien cuando el número de parámetros es de dimensión finita y la hipótesis nula especifica que \(\boldsymbol \theta\) está en el interior del espacio de parámetros.
La principal ventaja de la estadística de Wald es que solo requiere el cálculo de \(\boldsymbol \theta_{MLE}\) y no de \(\boldsymbol \theta_{Reduced}\). En contraste, la principal ventaja de la estadística de Rao es que solo requiere el cálculo de \(\boldsymbol \theta_{Reduced}\) y no de \(\boldsymbol \theta_{MLE}\). En muchas aplicaciones, el cálculo de \(\boldsymbol \theta_{MLE}\) es laborioso. La prueba de razón de verosimilitud es una extensión directa de la prueba \(F\) parcial introducida en el Capítulo 4: permite comparar directamente modelos anidados, una técnica útil en aplicaciones.
11.9.4 Criterios de Información
Las pruebas de razón de verosimilitud son útiles para elegir entre dos modelos que son anidados, es decir, donde un modelo es un subconjunto del otro. ¿Cómo comparamos modelos cuando no están anidados? Una forma es utilizar los siguientes criterios de información.
La distancia entre dos distribuciones de probabilidad dadas por funciones de densidad de probabilidad \(g\) y \(f_{\boldsymbol \theta}\) se puede resumir como \[ \mathrm{KL}(g,f_{\boldsymbol \theta}) = \mathrm{E}_g \ln \frac{g(y)}{f_{\boldsymbol \theta}(y)} . \] Esta es la distancia de Kullback-Leibler. Aquí, hemos indexado \(f\) con un vector de parámetros \(\boldsymbol \theta\). Si dejamos que la función de densidad \(g\) sea fija en un valor hipotético, digamos \(f_{{\boldsymbol \theta}_0}\), entonces minimizar \(\mathrm{KL}(f_{{\boldsymbol \theta}_0},f_{\boldsymbol \theta})\) es equivalente a maximizar el log-verosimilitud.
Sin embargo, maximizar la verosimilitud no impone una estructura suficiente en el problema porque sabemos que siempre podemos aumentar la verosimilitud introduciendo parámetros adicionales. Así, Akaike en 1974 mostró que una alternativa razonable es minimizar \[ AIC = -2 \times L(\boldsymbol \theta_{MLE}) + 2 \times (número~de~parámetros), \] conocido como Criterio de Información de Akaike. Aquí, el término adicional \(2 \times (número~de~parámetros)\) es una penalización por la complejidad del modelo. Con esta penalización, no se puede mejorar el ajuste simplemente introduciendo parámetros adicionales. Esta estadística se puede utilizar al comparar varios modelos alternativos que no necesariamente están anidados. Se elige el modelo que minimiza \(AIC\). Si los modelos bajo consideración tienen el mismo número de parámetros, esto es equivalente a elegir el modelo que maximiza el log-verosimilitud.
Observamos que esta definición no es adoptada uniformemente en la literatura. Por ejemplo, en análisis de series temporales, el \(AIC\) se reescala por el número de parámetros. Otras versiones que proporcionan correcciones para muestras finitas también están disponibles en la literatura.
Schwarz en 1978 derivó un criterio alternativo utilizando métodos bayesianos. Su medida se conoce como el Criterio de Información Bayesiano, definido como \[ BIC = -2 \times L(\boldsymbol \theta_{MLE}) + (número~de~parámetros) \times \ln (número~de~observaciones), \] Esta medida da un mayor peso al número de parámetros. Es decir, todo lo demás siendo igual, el \(BIC\) sugerirá un modelo más parsimonioso que el \(AIC\).
Al igual que el coeficiente de determinación ajustado \(R^2_a\) que hemos introducido en la literatura de regresión, tanto el \(AIC\) como el \(BIC\) proporcionan medidas de ajuste con una penalización por la complejidad del modelo. En los modelos de regresión lineal normal, la Sección 5.6 señaló que minimizar el \(AIC\) es equivalente a minimizar \(n \ln s^2 + k\). Otra estadística de regresión lineal que equilibra la bondad de ajuste y la complejidad del modelo es la estadística \(C_p\) de Mallows. Para \(p\) variables candidatas en el modelo, esto se define como \(C_p = (Error~SS)_p/s^2 - (n-2p).\) Véase, por ejemplo, Cameron y Trivedi (1998) para referencias y más discusión sobre criterios de información.