Capítulo 15 Temas Misceláneos de Regresión
Vista Previa del Capítulo. Este capítulo proporciona un recorrido rápido por varios temas de regresión que un analista probablemente encontrará en diferentes contextos de regresión. El objetivo de este capítulo es introducir estos temas, proporcionar definiciones e ilustrar contextos en los que estos temas pueden aplicarse.
15.1 Modelos Lineales Mixtos
Aunque los modelos lineales mixtos son una parte establecida de la metodología estadística, su uso no es tan generalizado como la regresión en aplicaciones actuariales y financieras. Por lo tanto, esta sección introduce este marco de modelado, comenzando con un caso especial ampliamente utilizado. Después de introducir el marco de modelado, esta sección describe la estimación de coeficientes de regresión y componentes de varianza.
Comenzamos con el modelo de efectos aleatorios unidireccional, con la ecuación del modelo \[\begin{equation} y_{it} = \mu + \alpha_i + \varepsilon_{it}, ~~~~~ t=1, \ldots, T_i, ~~ i=1,\ldots, n. \tag{15.1} \end{equation}\] Podemos usar este modelo para representar observaciones repetidas de un sujeto o grupo \(i\). El subíndice \(t\) se utiliza para denotar replicaciones que pueden ser en el tiempo o en múltiples membresías de grupo (como varios empleados en una empresa). Las observaciones repetidas en el tiempo fueron el enfoque del Capítulo 10.
Cuando hay solo una observación por grupo, de modo que \(T_i=1\), el término de perturbación representa la información no observable sobre la variable dependiente. Con observaciones repetidas, tenemos la oportunidad de capturar características no observables del grupo a través del término \(\alpha_i\). Aquí, se asume que \(\alpha_i\) es una variable aleatoria y se conoce como un efecto aleatorio. Otro enfoque, introducido en la Sección 4.3, representaba \(\alpha_i\) como un parámetro a estimar utilizando una variable explicativa categórica.
Para este modelo, \(\mu\) representa una media general, \(\alpha_i\) la desviación de la media debido a características no observadas del grupo y \(\varepsilon_{it}\) la variación de respuesta individual. Asumimos que \(\{\alpha_i\}\) son i.i.d. con media cero y varianza \(\sigma^2_{\alpha}\). Además, asumimos que \(\{\varepsilon_{it}\}\) son i.i.d. con media cero y varianza \(\sigma^2\) y son independientes de \(\alpha_i\).
Una extensión de la ecuación (15.1) es el modelo básico de efectos aleatorios descrito en la Sección 10.5, basado en la ecuación del modelo \[\begin{equation}\label{E15:BasicRE} y_{it} =\alpha_i + \mathbf{x}_{it}^{\prime} \boldsymbol \beta + \varepsilon_{it}. \tag{15.2} \end{equation}\] En esta extensión, la media general \(\mu\) se reemplaza por la función de regresión \(\mathbf{x}_{it}^{\prime} \boldsymbol \beta\). Este modelo incluye efectos aleatorios (\(\alpha_i\)) así como efectos fijos (\(\mathbf{x}_{it}\)). Los modelos mixtos son aquellos que incluyen efectos aleatorios y fijos.
Apilando las ecuaciones del modelo de manera apropiada, se obtiene una expresión para el modelo lineal mixto: \[\begin{equation} \mathbf{y} = \mathbf{Z} \boldsymbol \alpha + \mathbf{X} \boldsymbol \beta +\boldsymbol \varepsilon . \tag{15.3} \end{equation}\] Aquí, \(\mathbf{y}\) es un vector \(N \times 1\) de variables dependientes, \(\boldsymbol \varepsilon\) es un vector \(N \times 1\) de errores, Z y X son matrices conocidas \(N \times q\) y \(N \times k\) de variables explicativas, respectivamente, y \(\boldsymbol \alpha\) y \(\boldsymbol \beta\) son vectores desconocidos \(q \times 1\) y \(k \times 1\) de parámetros. En el modelo lineal mixto, los parámetros \(\boldsymbol \beta\) son fijos (no estocásticos) y los parámetros \(\boldsymbol \alpha\) son aleatorios (estocásticos).
Para la estructura de la media, asumimos E(\(\mathbf{y}|\boldsymbol \alpha) = \mathbf{Z} \boldsymbol \alpha + \mathbf{X} \boldsymbol \beta\) y E \(\boldsymbol \alpha = \mathbf{0}\), de modo que \(\mathrm{E}~\mathbf{y} = \mathbf{X} \boldsymbol \beta\). Para la estructura de covarianza, asumimos Var(\(\mathbf{y}|\boldsymbol \alpha) = \mathbf{R}\), Var(\(\boldsymbol \alpha)= \mathbf{D}\) y Cov(\(\boldsymbol \alpha,\boldsymbol \varepsilon ^{\prime} )= \mathbf{0}\). Esto da como resultado Var \(\mathbf{y} = \mathbf{Z D Z}^{\prime} + \mathbf{R = V}\). En aplicaciones longitudinales, la matriz \(\mathbf{R}\) se utiliza para modelar la correlación serial intra-sujeto.
El modelo lineal mixto es bastante general e incluye muchos modelos como casos especiales. Para un tratamiento en profundidad de los modelos lineales mixtos, ver Pinheiro y Bates (2000). Para ilustrar, volvemos al modelo básico de efectos aleatorios en la ecuación (15.2). Apilando las replicaciones del grupo \(i\)-ésimo, podemos escribir \[ \mathbf{y}_i = \alpha_i \mathbf{1}_i + \mathbf{X}_i \boldsymbol \beta +\boldsymbol \varepsilon_i, \] donde \(\mathbf{y}_i = (y_{i1} , \ldots, y_{iT_i})^{\prime}\) es el vector de variables dependientes, \(\boldsymbol \varepsilon_i = ( \varepsilon_{i1} , \ldots, \varepsilon_{iT_i})^{\prime}\) es el vector correspondiente de términos de perturbación, \(\mathbf{X}_i = (\mathbf{x}_{i1} , \ldots, \mathbf{x}_{iT_i})^{\prime}\) es la matriz \(T_i \times k\) de variables explicativas y \(\mathbf{1}_i\) es un vector \(T_i \times 1\) de unos. Apilando los grupos \(i=1, \ldots, n\), se obtiene la ecuación (15.3) con \(\mathbf{y} = (\mathbf{y}_1^{\prime} , \ldots, \mathbf{y}_n^{\prime})^{\prime}\), \(\boldsymbol \varepsilon = (\boldsymbol \varepsilon_1 ^{\prime}, \ldots, \boldsymbol \varepsilon_n^{\prime})^{\prime}\), \(\boldsymbol \alpha = ( \alpha _1 , \ldots, \alpha _n)^{\prime}\),
\[ \mathbf{X}= \left( \begin{array}{c} \mathbf{X}_1 \\ \vdots \\ \mathbf{X}_n \\ \end{array} \right) ~~~~\mathrm{y}~~~~ \mathbf{Z}= \left( \begin{array}{cccc} \mathbf{1}_1 & \mathbf{0} & \cdots & \mathbf{0}\\ \mathbf{0} & \mathbf{1}_2 & \cdots & \mathbf{0}\\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{0} & \mathbf{0}& \cdots & \mathbf{1}_n\\ \end{array} \right) . \]
La estimación del modelo lineal mixto se realiza en dos etapas. En la primera etapa, estimamos los coeficientes de regresión \(\boldsymbol \beta\), asumiendo conocimiento de la matriz de varianza-covarianza \(\mathbf V\). Luego, en la segunda etapa, se estiman los componentes de la matriz de varianza-covarianza \(\mathbf V\).
15.1.1 Mínimos Cuadrados Ponderados
En la Sección 5.7.3, introdujimos la noción de estimaciones de mínimos cuadrados ponderados de los coeficientes de regresión de la forma \[\begin{equation} \mathbf{b}_{WLS} = \left(\mathbf{X}^{\prime} \mathbf{W}\mathbf{X} \right)^{-1}\mathbf{X}^{\prime} \mathbf{W}\mathbf{y} . \tag{15.4} \end{equation}\] La matriz \(n \times n\) \(\mathbf{W}\) se eligió de la forma \(\mathbf{W} = diag(w_i)\), de modo que el elemento diagonal \(i\)-ésimo de \(\mathbf{W}\) es un peso \(w_i\). Como se introdujo en la Sección 5.7.3, esto nos permitió ajustar modelos de regresión heterocedásticos.
Más generalmente, podemos permitir que \(\mathbf{W}\) sea cualquier matriz (simétrica) (tal que \(\mathbf{X}^{\prime} \mathbf{W}\mathbf{X}\) sea invertible). Esta extensión nos permite acomodar otros tipos de dependencias que aparecen, por ejemplo, en modelos lineales mixtos. Asumiendo únicamente que E \(\mathbf{y} = \mathbf{X} \boldsymbol \beta\) y Var \(\mathbf{y} = \mathbf{V}\), es fácil establecer \[\begin{equation} \mathrm{E}~\mathbf{b}_{WLS} = \boldsymbol \beta \tag{15.5} \end{equation}\] y \[\begin{equation} \mathrm{Var}~\mathbf{b}_{WLS} = \left(\mathbf{X}^{\prime} \mathbf{W}\mathbf{X} \right)^{-1} \left(\mathbf{X}^{\prime} \mathbf{W}\mathbf{V}\mathbf{W}\mathbf{X} \right) \left(\mathbf{X}^{\prime} \mathbf{W}\mathbf{X} \right)^{-1} . \tag{15.6} \end{equation}\] La ecuación (15.5) indica que \(\mathbf{b}_{WLS}\) es un estimador insesgado de \(\boldsymbol \beta\). La ecuación (15.6) es un resultado básico que se utiliza para la inferencia estadística, incluyendo la evaluación de errores estándar.
La mejor elección de la matriz de pesos es el inverso de la matriz de varianza-covarianza, de modo que \(\mathbf{W}=\mathbf{V}^{-1}\). Esta elección resulta en el estimador de mínimos cuadrados generalizados, comúnmente denotado por el acrónimo \(GLS\). La varianza es \[\begin{equation} \mathrm{Var}~\mathbf{b}_{GLS} = \left(\mathbf{X}^{\prime} \mathbf{V}^{-1}\mathbf{X} \right)^{-1} . \tag{15.7} \end{equation}\] Esto es óptimo en el sentido de que se puede demostrar que \(\mathbf{b}_{GLS} = \left(\mathbf{X}^{\prime} \mathbf{V}^{-1}\mathbf{X} \right)^{-1}\mathbf{X}^{\prime} \mathbf{V}^{-1}\mathbf{y}\) tiene varianza mínima entre la clase de todos los estimadores insesgados del vector de parámetros \(\boldsymbol \beta\). Esta propiedad se conoce como el \(Teorema~de~Gauss-Markov\), una extensión para matrices de varianza-covarianza generales \(\mathbf{V}\) de la propiedad introducida en la Sección 3.2.3.
15.1.2 Estimación de Componentes de Varianza
La estimación por mínimos cuadrados generalizados asume que \(\mathbf{V}\) es conocida, al menos hasta una constante escalar. Por supuesto, es poco probable que una matriz general \(n \times n\) \(\mathbf{V}\) pueda ser estimada a partir de \(n\) observaciones. Sin embargo, es posible y rutinario estimar casos especiales de \(\mathbf{V}\). Sea \(\boldsymbol \tau\) el vector de parámetros que indexan \(\mathbf{V}\); una vez que \(\boldsymbol \tau\) es conocido, la matriz \(\mathbf{V}\) está completamente especificada. Llamamos componentes de varianza a los elementos de \(\boldsymbol \tau\). Por ejemplo, en nuestro caso básico de regresión, tenemos \(\mathbf{V} = \sigma^2 \mathbf{I}\), por lo que \(\boldsymbol \tau = \sigma^2\). Como otro ejemplo, en el modelo básico de efectos aleatorios unidireccionales, la estructura de varianza está descrita por los componentes de varianza \(\boldsymbol \tau = (\sigma^2, \sigma^2_{\alpha})^{\prime}\).
Existen varios métodos para estimar componentes de varianza, algunos basados en verosimilitud y otros que usan el método de momentos. Estos métodos están disponibles en software estadístico. Para dar a los lectores una idea de los cálculos involucrados, esbozamos brevemente el procedimiento basado en máxima verosimilitud utilizando distribuciones normales.
Para observaciones \(\mathbf{y}\) distribuidas normalmente con media E \(\mathbf{y} = \mathbf{X} \boldsymbol \beta\) y Var \(\mathbf{y} = \mathbf{V} = \mathbf{V (\boldsymbol \tau)}\), la verosimilitud logarítmica está dada por \[\begin{equation} L(\boldsymbol \beta, \boldsymbol \tau ) = - \frac{1}{2} \left[ N \ln (2 \pi) + \ln \det (\mathbf{V (\boldsymbol \tau)}) + (\mathbf{y} - \mathbf{X} \boldsymbol \beta)^{\prime} \mathbf{V (\boldsymbol \tau)}^{-1} (\mathbf{y} - \mathbf{X} \boldsymbol \beta) \right]. \tag{15.8} \end{equation}\]
Esta verosimilitud logarítmica debe maximizarse en términos de los parámetros \(\boldsymbol \beta\) y \(\boldsymbol \tau\). En la primera etapa, mantenemos \(\boldsymbol \tau\) fijo y maximizamos la ecuación (15.8) sobre \(\boldsymbol \beta\). Cálculos agradables muestran que \(\mathbf{b}_{GLS}\) es, de hecho, el estimador de máxima verosimilitud de \(\boldsymbol \beta\). Insertando esto en la ecuación (15.8), obtenemos la verosimilitud “perfilada” \[\begin{equation} \small{ L_P(\boldsymbol \tau ) = L(\mathbf{b}_{GLS}, \boldsymbol \tau ) \propto - \frac{1}{2}\left[ \ln \det (\mathbf{V (\boldsymbol \tau)}) + (\mathbf{y} - \mathbf{X} \mathbf{b}_{GLS})^{\prime} \mathbf{V (\boldsymbol \tau)}^{-1} (\mathbf{y} - \mathbf{X} \mathbf{b}_{GLS}) \right], } \tag{15.9} \end{equation}\] donde hemos eliminado las constantes que no dependen de \(\boldsymbol \tau\). (El símbolo \(\propto\) significa “es proporcional a.”)
Para implementar este procedimiento de dos etapas, el software informático generalmente utiliza estimaciones de mínimos cuadrados ordinarios (OLS) b como valores iniciales. Luego, en la segunda etapa, se determinan las estimaciones de \(\boldsymbol \tau\) mediante métodos iterativos (optimización numérica) buscando los valores de \(\boldsymbol \tau\) que maximizan \(L(\mathbf{b},\boldsymbol \tau)\). Estas estimaciones se utilizan para actualizar las estimaciones de los coeficientes de regresión utilizando mínimos cuadrados ponderados. Este proceso continúa hasta alcanzar la convergencia.
Hay dos ventajas en este procedimiento de dos etapas. Primero, al desacoplar la regresión de la estimación de los parámetros de los componentes de varianza, podemos aplicar cualquier método que deseemos a los componentes de varianza y luego “insertar” estas estimaciones en el componente de regresión (estimación de mínimos cuadrados generalizados estimados). Segundo, tenemos una expresión en forma cerrada para las estimaciones de la regresión. Esto es más rápido computacionalmente que los métodos iterativos requeridos por las rutinas generales de optimización.
15.1.3 Mejor Predicción Lineal Insesgada
Esta sección desarrolla las mejores predicciones lineales insesgadas (BLUPs, por sus siglas en inglés) en el contexto de modelos lineales mixtos. Introducimos BLUPs como el predictor de error cuadrático medio mínimo de una variable aleatoria, w. Este desarrollo es originalmente debido a Goldberger (1962), quien acuñó el término “mejor predictor lineal insesgado”. El acrónimo BLUP fue utilizado por primera vez por Henderson (1973).
El objetivo genérico es predecir una variable aleatoria w, tal que \(\mathrm{E}~ w = \boldsymbol \lambda ^{\prime} \boldsymbol \beta\) y \(\mathrm{Var}~ w = \sigma^2_w\). Denotamos la covarianza entre \(w\) y \(\mathbf{y}\) como el vector \(1 \times N\) \(\mathrm{Cov}(w,\mathbf{y}) = \mathrm{E}\{(w-\mathrm{E}w)(\mathbf{y}-\mathrm{E}\mathbf{y})^{\prime} \}\). La elección de \(w\), y por ende \(\boldsymbol \lambda\) y \(\sigma^2_w\), dependerá de la aplicación.
Bajo estas suposiciones, se puede demostrar que el \(BLUP\) de \(w\) es \[\begin{equation} w_{BLUP} = \boldsymbol \lambda ^{\prime} \mathbf{b}_{GLS} + \mathrm{Cov}(w,\mathbf{y})\mathbf{V}^{-1}(\mathbf{y}-\mathbf{X} \mathbf{b}_{GLS}). \tag{15.10} \end{equation}\] Los predictores \(BLUP\) son óptimos, asumiendo que los componentes de varianza implícitos en \(\mathbf{V}\) y \(\mathrm{Cov}(w,\mathbf{y})\) son conocidos. Las aplicaciones de BLUP típicamente requieren que los componentes de varianza sean estimados, como se describe en la Sección 15.1.2. Los BLUPs con componentes de varianza estimados se conocen como BLUPs empíricos o EBLUPs.
Hay tres tipos importantes de elección para \(w\):
- \(w=\varepsilon\), lo que resulta en los denominados “residuos \(BLUP\)”,
- efectos aleatorios, como \(\boldsymbol \alpha\), y
- observaciones futuras, resultando en pronósticos óptimos.
Para la primera elección, encontrará que los residuos \(BLUP\) están regularmente codificados en los paquetes de software estadístico que ajustan modelos lineales mixtos. Para la segunda elección, al dejar que \(w\) sea una combinación lineal arbitraria de efectos aleatorios, se puede demostrar que el predictor \(BLUP\) de \(\boldsymbol \alpha\) es \[\begin{equation} \mathbf{a}_{BLUP} = \mathbf{D Z}^{\prime} \mathbf{V}^{-1} (\mathbf{y} - \mathbf{X b}_{GLS}). \tag{15.11} \end{equation}\] Para ejemplos de la tercera elección, pronósticos con modelos lineales mixtos, nos referimos a Frees (2004, Capítulos 4 y 8).
Para considerar una aplicación de la ecuación (15.11), considere lo siguiente.
Caso especial: Modelo de Efectos Aleatorios Unidireccionales. Considere el modelo basado en la ecuación (15.1) y suponga que deseamos estimar la media condicional del grupo \(i\), \(w=\mu + \alpha_i.\) Luego, cálculos directos (ver Frees, 2004, Capítulo 4) basados en la ecuación (15.11) muestran que el \(BLUP\) es \[\begin{equation} \zeta_i \bar{y}_i + (1-\zeta_i ) m_{\alpha,GLS} , \tag{15.12} \end{equation}\] con peso \(\zeta_i = T_i /(T_i + \sigma^2/\sigma^2_{\alpha})\) y la estimación \(GLS\) de \(\mu\), \(m_{\alpha,GLS} = \sum_i \zeta_i \bar{y}_i / \sum_i \zeta_i\). En el Capítulo 18, interpretaremos \(\zeta_i\) como un factor de credibilidad.
15.2 Regresión Bayesiana
En los modelos estadísticos bayesianos, se considera que tanto los parámetros del modelo como los datos son variables aleatorias. En esta sección, usamos un tipo específico de modelo bayesiano, el modelo jerárquico lineal normal discutido, por ejemplo, por Gelman et al. (2004). Como en el esquema de muestreo en dos etapas descrito en la Sección 3.3.1, el modelo jerárquico lineal se especifica en etapas. Específicamente, consideramos la siguiente jerarquía de dos niveles:
- Dado los parámetros \(\boldsymbol \alpha\) y \(\boldsymbol \beta\), el modelo de respuesta es \(\mathbf{y} = \mathbf{Z}\boldsymbol \alpha + \mathbf{X}\boldsymbol \beta + \boldsymbol \varepsilon\). Este nivel es un modelo lineal ordinario (fijo) que se introdujo en los Capítulos 3 y 4. Específicamente, asumimos que el vector de respuestas \(\mathbf{y}\) condicionado a \(\boldsymbol \alpha\) y \(\boldsymbol \beta\) está normalmente distribuido y que E (\(\mathbf{y} | \boldsymbol \alpha, \boldsymbol \beta ) = \mathbf{Z}\boldsymbol \alpha + \mathbf{X}\boldsymbol \beta\) y Var (\(\mathbf{y} | \boldsymbol \alpha, \boldsymbol \beta) = \mathbf{R}\).
- Asumimos que \(\boldsymbol \alpha\) está distribuido normalmente con media \(\boldsymbol{\mu _{\alpha}}\) y varianza \(\mathbf{D}\) y que \(\boldsymbol \beta\) está distribuido normalmente con media \(\boldsymbol{\mu _{\beta}}\) y varianza \(\boldsymbol{\Sigma _{\beta}}\), cada uno independiente del otro.
Las diferencias técnicas entre el modelo lineal mixto y el modelo jerárquico lineal normal son:
- En el modelo lineal mixto, \(\boldsymbol \beta\) es un parámetro fijo desconocido, mientras que en el modelo jerárquico lineal normal, \(\boldsymbol \beta\) es un vector aleatorio, y
- el modelo lineal mixto no hace suposiciones de distribución, mientras que en el modelo jerárquico lineal normal se hacen suposiciones de distribución en cada etapa.
Además, hay diferencias importantes en la interpretación. Para ilustrar, suponga que \(\boldsymbol \beta= \mathbf{0}\) con probabilidad uno. En la interpretación clásica no bayesiana, también conocida como frecuentista, pensamos en la distribución de \(\{\boldsymbol \alpha\}\) como representativa de la probabilidad de obtener una realización de \(\boldsymbol \alpha _i\). Esta interpretación es adecuada cuando tenemos una población de empresas o personas, y cada realización es un muestreo de esa población. En contraste, en el caso bayesiano, se interpreta la distribución de \(\{\boldsymbol \alpha\}\) como representativa del conocimiento que se tiene de este parámetro. Esta distribución puede ser subjetiva y permite al analista inyectar formalmente sus evaluaciones en el modelo. En este sentido, la interpretación frecuentista puede considerarse un caso especial del marco bayesiano.
La distribución conjunta de \((\boldsymbol \alpha^{\prime}, \boldsymbol \beta^{\prime})^{\prime}\) se conoce como la distribución a priori. Para resumir, la distribución conjunta de \((\boldsymbol \alpha^{\prime}, \boldsymbol \beta^{\prime}, \mathbf{y}^{\prime})^{\prime}\) es
\[\begin{equation} \left( \begin{array}{c} \boldsymbol \alpha \\ \boldsymbol \beta \\ \mathbf{y} \\ \end{array} \right) \sim N \left( \left( \begin{array}{c} \boldsymbol {\mu_{\alpha}} \\ \boldsymbol {\mu_{\beta}} \\ \mathbf{Z}\boldsymbol {\mu_{\alpha}} + \mathbf{X}\boldsymbol {\mu_{\beta}} \\ \end{array} \right) , \left(\begin{array}{ccc} \mathbf{D} & \mathbf{0} & \mathbf{DZ}^{\prime} \\ \mathbf{0} & \boldsymbol {\Sigma_{\beta}} & \boldsymbol {\Sigma_{\beta}}\mathbf{X}^{\prime} \\ \mathbf{ZD} & \mathbf{X}\boldsymbol {\Sigma_{\beta}} & \mathbf{V} + \mathbf{X}\boldsymbol {\Sigma_{\beta}} \mathbf{X}^{\prime}\\ \end{array} \right) \right) , \tag{15.13} \end{equation}\] donde \(\mathbf{V = R + Z D }\mathbf{Z}^{\prime}\).
La distribución de los parámetros dados los datos se conoce como la distribución posterior. Para calcular esta distribución condicional, utilizamos resultados estándar del análisis multivariado. Específicamente, la distribución posterior de \((\boldsymbol \alpha^{\prime}, \boldsymbol \beta^{\prime})^{\prime}\) dado \(\mathbf{y}\) es normal. No es difícil verificar que la media condicional es \[\begin{equation} \mathrm{E}~ \left( \begin{array}{c} \boldsymbol \alpha \\ \boldsymbol \beta \\ \end{array} \right) | \mathbf{y} = \left( \begin{array}{c} \boldsymbol {\mu_{\alpha}} + \mathbf{DZ}^{\prime} (\mathbf{V} + \mathbf{X}\boldsymbol {\Sigma_{\beta}} \mathbf{X}^{\prime})^{-1} (\mathbf{y} -\mathbf{Z}\boldsymbol {\mu_{\alpha}} - \mathbf{X}\boldsymbol {\mu_{\beta}}) \\ \boldsymbol {\mu_{\beta}} + \boldsymbol {\Sigma_{\beta}}\mathbf{X}^{\prime} (\mathbf{V} + \mathbf{X}\boldsymbol {\Sigma_{\beta}} \mathbf{X}^{\prime})^{-1} (\mathbf{y} -\mathbf{Z}\boldsymbol {\mu_{\alpha}} - \mathbf{X}\boldsymbol {\mu_{\beta}}) \\ \end{array} \right) . \tag{15.14} \end{equation}\]
Hasta este punto, el tratamiento de los parámetros \(\boldsymbol \alpha\) y \(\boldsymbol \beta\) ha sido simétrico. En algunas aplicaciones, como con datos longitudinales, generalmente se tiene más información sobre los parámetros globales \(\boldsymbol \beta\) que sobre los parámetros específicos del sujeto \(\boldsymbol \alpha\). Para ver cómo cambia la distribución posterior dependiendo de la cantidad de información disponible, consideramos dos casos extremos.
Primero, considere el caso \(\boldsymbol{\Sigma _{\beta}}= \mathbf{0}\), de modo que \(\boldsymbol \beta=\boldsymbol{\mu _{\beta}}\) con probabilidad uno. Intuitivamente, esto significa que \(\boldsymbol \beta\) es conocido con precisión, generalmente a partir de información colateral. Luego, a partir de la ecuación (15.14), tenemos
\[\begin{equation} \mathrm{E}~ ( \boldsymbol \alpha | \mathbf{y}) = \boldsymbol {\mu_{\alpha}} + \mathbf{DZ}^{\prime} \mathbf{V}^{-1} (\mathbf{y} -\mathbf{Z}\boldsymbol {\mu_{\alpha}} - \mathbf{X}\boldsymbol \beta) . \tag{15.15} \end{equation}\] Asumiendo que \(\boldsymbol{\mu _{\alpha}}= \mathbf{0}\), el mejor estimador lineal insesgado de E (\(\boldsymbol \alpha | \mathbf{y}\)) es \[ \mathbf{a}_{BLUP} = \mathbf{D Z}^{\prime} \mathbf{V}^{-1} (\mathbf{y} - \mathbf{X b}_{GLS}). \] Recuerde de la ecuación (15.11) que \(\mathbf{a}_{BLUP}\) es también el mejor predictor lineal insesgado en el marco de modelo frecuentista (no bayesiano).
En segundo lugar, considere el caso en que \(\boldsymbol{\Sigma _{\beta}}^{-1}= \mathbf{0}\). En este caso, la información previa sobre el parámetro \(\boldsymbol \beta\) es vaga; esto se conoce como usar una priori difusa. En este caso, se puede verificar que
\[ \mathrm{E}~ (\boldsymbol \alpha | \mathbf{y}) \rightarrow \mathbf{a}_{BLUP}, \] a medida que \(\boldsymbol{\Sigma _{\beta}}^{-1}\rightarrow \mathbf{0}\). (Ver, por ejemplo, Frees, 2004, Sección 4.6.)
Así, es interesante que en ambos casos extremos, llegamos a la estadística \(\mathbf{a}_{BLUP}\) como un predictor de \(\boldsymbol \alpha\). Este análisis asume que \(\mathbf{D}\) y \(\mathbf{R}\) son matrices de parámetros fijos. También es posible asumir distribuciones para estos parámetros; típicamente, se utilizan distribuciones de Wishart independientes para \(\mathbf{D}^{-1}\) y \(\mathbf{R}^{-1}\), ya que son prioris conjugadas. Alternativamente, se pueden estimar \(\mathbf{D}\) y \(\mathbf{R}\) usando los métodos descritos en la Sección 15.1. La estrategia general de sustituir estimaciones puntuales por ciertos parámetros en una distribución posterior se llama estimación bayesiana empírica.
Para examinar casos intermedios, consideramos el siguiente caso especial. Generalizaciones pueden encontrarse en Luo, Young y Frees (2001).
Caso Especial: Modelo de Efectos Aleatorios Unidireccionales. Retomamos el modelo considerado en la ecuación (15.2) y, para simplificar, asumimos datos balanceados de modo que \(T_i = T\). El objetivo es determinar las distribuciones posteriores de los parámetros. Con fines ilustrativos, nos enfocamos en las medias posteriores. Así, reescribiendo la ecuación (15.2), el modelo es \[ y_{it} = \beta + \alpha_i + \varepsilon_{it}, \] donde usamos \(\beta \sim N(\mu_{\beta}, \sigma^2_{\beta})\) en lugar de la media fija \(\mu\). La distribución previa de \(\alpha_i\) es independiente con \(\alpha_i \sim N(0, \sigma^2_{\alpha})\).
Usando la ecuación (15.14), obtenemos la media posterior de \(\beta\), \[\begin{equation} \hat{\beta} = \mathrm{E}~(\beta| \mathbf{y}) = \left( \frac{1}{\sigma^2_{\beta}}+ \frac{nT}{\sigma^2_{\varepsilon}+T\sigma^2_{\alpha}} \right)^{-1} \left( \frac{nT}{\sigma^2_{\varepsilon}+T\sigma^2_{\alpha}} \bar{y} + \frac{\mu}{\sigma^2_{\beta}} \right) , \tag{15.16} \end{equation}\] después de algo de álgebra. Así, \(\hat{\beta}\) es un promedio ponderado de la media muestral, \(\bar{y}\), y la media previa, \(\mu_{\beta}\). Es fácil ver que \(\hat{\beta}\) se aproxima a la media muestral a medida que \(\sigma^2_{\beta} \rightarrow \infty\), es decir, cuando la información previa sobre \(\beta\) se vuelve “vaga”. Por el contrario, \(\hat{\beta}\) se aproxima a la media previa \(\mu_{\beta}\) a medida que \(\sigma^2_{\beta} \rightarrow 0\), es decir, cuando la información previa se vuelve “precisa”.
De manera similar, utilizando la ecuación (15.14), la media posterior de \(\alpha_i\) es \[ \hat{\alpha_i} = \mathrm{E}~(\alpha_i | \mathbf{y}) = \zeta \left[ ( \bar{y}_i - \mu_{\beta} ) - \zeta_{\beta} (\bar{y} - \mu_{\beta} ) \right], \] donde tenemos que \[ \zeta = \frac{T \sigma^2_{\alpha}}{\sigma^2_{\varepsilon}+T \sigma^2_{\alpha}} \] y definimos \[ \zeta_{\beta} = \frac{nT \sigma^2_{\beta}}{\sigma^2_{\varepsilon}+T \sigma^2_{\alpha}+nT \sigma^2_{\beta}}. \] Nótese que \(\zeta_{\beta}\) mide la precisión del conocimiento sobre \(\beta\). Específicamente, vemos que \(\zeta_{\beta}\) se aproxima a uno cuando \(\sigma^2_{\beta} \rightarrow \infty\), y se aproxima a cero cuando \(\sigma^2_{\beta} \rightarrow 0\).
Combinando estos dos resultados, tenemos que \[ \hat{\alpha_i} +\hat{\beta} = (1-\zeta_{\beta}) \left[ (1-\zeta) \mu_{\beta} + \zeta \bar{y}_i \right] + \zeta_{\beta} \left[ (1-\zeta)\bar{y} + \zeta\bar{y}_i \right]. \] Así, si nuestro conocimiento de la distribución de \(\beta\) es vago, entonces \(\zeta_{\beta} =1\) y el predictor se reduce a la expresión en la ecuación (15.12) (para datos balanceados). Por el contrario, si nuestro conocimiento de la distribución de \(\beta\) es preciso, entonces \(\zeta_{\beta} =0\) y el predictor se reduce a la expresión dada en el Capítulo 18. Con la formulación bayesiana, podemos considerar situaciones donde el conocimiento está disponible, aunque sea impreciso.
En resumen, hay varias ventajas del enfoque bayesiano. Primero, se puede describir toda la distribución de los parámetros condicionales a los datos. Esto permite, por ejemplo, proporcionar declaraciones de probabilidad respecto a la verosimilitud de los parámetros. Segundo, este enfoque permite a los analistas combinar información conocida de otras fuentes con los datos de manera coherente. En nuestro desarrollo, asumimos que la información puede conocerse a través del vector de parámetros \(\boldsymbol \beta\), con su confiabilidad controlada mediante la matriz de dispersión \(\boldsymbol{\Sigma_{\beta}}\). Valores de \(\boldsymbol{\Sigma_{\beta}}=\mathbf{0}\) indican completa confianza en los valores de \(\boldsymbol{\mu_{\beta}}\), mientras que valores de \(\boldsymbol{\Sigma_{\beta}}^{-1}=\mathbf{0}\) indican completa dependencia de los datos en lugar de conocimiento previo.
Tercero, el enfoque bayesiano proporciona un enfoque unificado para estimar \((\boldsymbol \alpha, \boldsymbol \beta)\). La Sección 15.1 sobre métodos no bayesianos requería una subsección separada sobre la estimación de componentes de varianza. En contraste, en métodos bayesianos, todos los parámetros pueden tratarse de manera similar. Esto es conveniente para explicar resultados a los consumidores del análisis de datos. Cuarto, el análisis bayesiano es particularmente útil para pronosticar respuestas futuras.
15.3 Estimación de Densidad y Suavizado de Diagramas de Dispersión
Al explorar una variable o relaciones entre dos variables, a menudo se desea obtener una idea general de los patrones sin imponer relaciones funcionales estrictas. Generalmente, los procedimientos gráficos funcionan bien porque podemos comprender relaciones potencialmente no lineales más fácilmente de manera visual que con resúmenes numéricos. Esta sección introduce la (estimación de densidad con núcleo) para visualizar la distribución de una variable y el suavizado de diagramas de dispersión para visualizar la relación entre dos variables.
Para obtener una impresión rápida de la distribución de una variable, un histograma es fácil de calcular e interpretar. Sin embargo, como se sugirió en el Capítulo 1, cambiar la ubicación y el tamaño de los rectángulos que comprenden el histograma puede dar diferentes impresiones de la distribución a los espectadores. Para introducir una alternativa, supongamos que tenemos una muestra aleatoria \(y_1, \ldots, y_n\) de una función de densidad de probabilidad \(f(.)\). Definimos el estimador de densidad con núcleo como \[ \hat{\mathrm{f}}(y) = \frac{1}{n b_n} \sum_{i=1}^n \mathrm{k}\left(\frac{y-y_i}{b_n}\right), \] donde \(b_n\) es un número pequeño llamado ancho de banda y k(.) es una función de densidad de probabilidad llamada núcleo.
Para desarrollar la intuición, primero consideramos el caso donde el núcleo k(.) es una función de densidad de probabilidad para una distribución uniforme en (-1,1). Para el núcleo uniforme, el estimador de densidad con núcleo cuenta el número de observaciones \(y_i\) que están dentro de \(b_n\) unidades de \(y\), y luego expresa la estimación de la densidad como el conteo dividido por el tamaño de la muestra multiplicado por el ancho del rectángulo (es decir, el conteo dividido por \(n \times 2 b_n\)). De esta manera, puede considerarse un estimador de histograma “local” en el sentido de que el centro del histograma depende del argumento \(y\).
Existen varias posibilidades para el núcleo. Algunas opciones ampliamente utilizadas son:
- el núcleo uniforme, \(\mathrm{k}(u) = \frac{1}{2}\) para \(-1 \leq u \leq 1\) y 0 en otro caso,
- el núcleo “Epanechikov”, \(\mathrm{k}(u) = \frac{3}{4}(1-u^2)\) para \(-1 \leq u \leq 1\) y 0 en otro caso, y
- el núcleo gaussiano, \(\mathrm{k}(u) = \phi(u)\) para \(-\infty < u < \infty\), la función de densidad normal estándar.
El núcleo Epanechnikov es una versión más suave que utiliza un polinomio cuadrático para que no se usen rectángulos discontinuos. El núcleo gaussiano es aún más continuo en el sentido de que el dominio ya no es más o menos \(b_n\) sino toda la recta real.
El ancho de banda \(b_n\) controla la cantidad de promedio. Para ver los efectos de diferentes elecciones de ancho de banda, consideremos un conjunto de datos sobre la utilización de hogares de ancianos que se introducirá en la Sección 17.3.2. Aquí, consideramos las tasas de ocupación, una medida de la utilización de hogares de ancianos. Un valor de 100 significa ocupación completa, aunque debido a la forma en que se construye esta medida, es posible que los valores superen 100. Específicamente, hay \(n=349\) tasas de ocupación que se muestran en la Figura 15.1. Ambas figuras utilizan un núcleo gaussiano. El panel izquierdo está basado en un ancho de banda de 0.1. Este panel parece muy irregular; el ancho de banda relativamente pequeño significa que se realiza poco promedio. Para los puntos atípicos, cada pico representa una sola observación. En contraste, el panel derecho está basado en un ancho de banda de 1.374. En comparación con el panel izquierdo, esta imagen muestra un panorama más suave, permitiendo al analista buscar patrones sin distraerse con bordes irregulares. Desde este panel, podemos ver fácilmente que la mayor parte de la masa está por debajo del 100 por ciento. Además, la distribución tiene sesgo hacia la izquierda, con valores entre 100 y 120 siendo raros.
El ancho de banda 1.374 se seleccionó utilizando un procedimiento automático incorporado en el software. Estos procedimientos automáticos eligen el ancho de banda para encontrar el mejor equilibrio entre la precisión y la suavidad de las estimaciones. (Para esta figura, utilizamos el software estadístico “R” que tiene incorporado el procedimiento de Silverman).
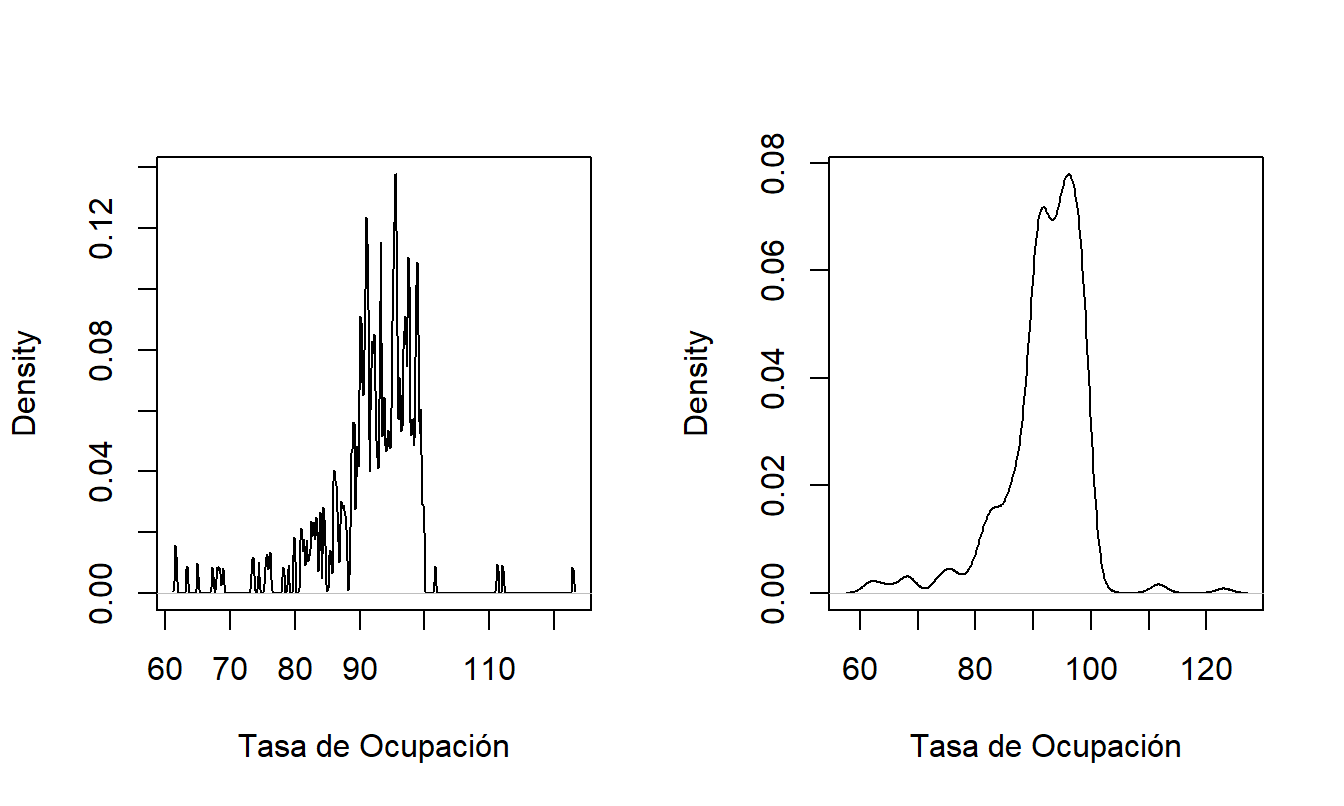
Figura 15.1: Estimaciones de Densidad con Núcleo de las Tasas de Ocupación de Hogares de Ancianos con Diferentes Anchos de Banda. El panel izquierdo está basado en un ancho de banda = 0.1, el panel derecho está basado en un ancho de banda = 1.374.
Las estimaciones de densidad con núcleo también dependen de la elección del núcleo, aunque esto es típicamente mucho menos importante en las aplicaciones que la elección del ancho de banda. Para mostrar los efectos de diferentes núcleos, mostramos solo las \(n=3\) tasas de ocupación que excedieron 110 en la Figura 15.2. El panel izquierdo muestra la superposición de histogramas rectangulares basados en el núcleo uniforme. Los núcleos más suaves de Epanechnikov y gaussiano en los paneles del medio y derecho son visualmente indistinguibles. A menos que esté trabajando con tamaños de muestra muy pequeños, generalmente no necesitará preocuparse por la elección del núcleo. Algunos analistas prefieren el núcleo uniforme debido a su interpretabilidad, otros prefieren el gaussiano debido a su suavidad y otros prefieren el núcleo de Epanechnikov como un compromiso razonable.
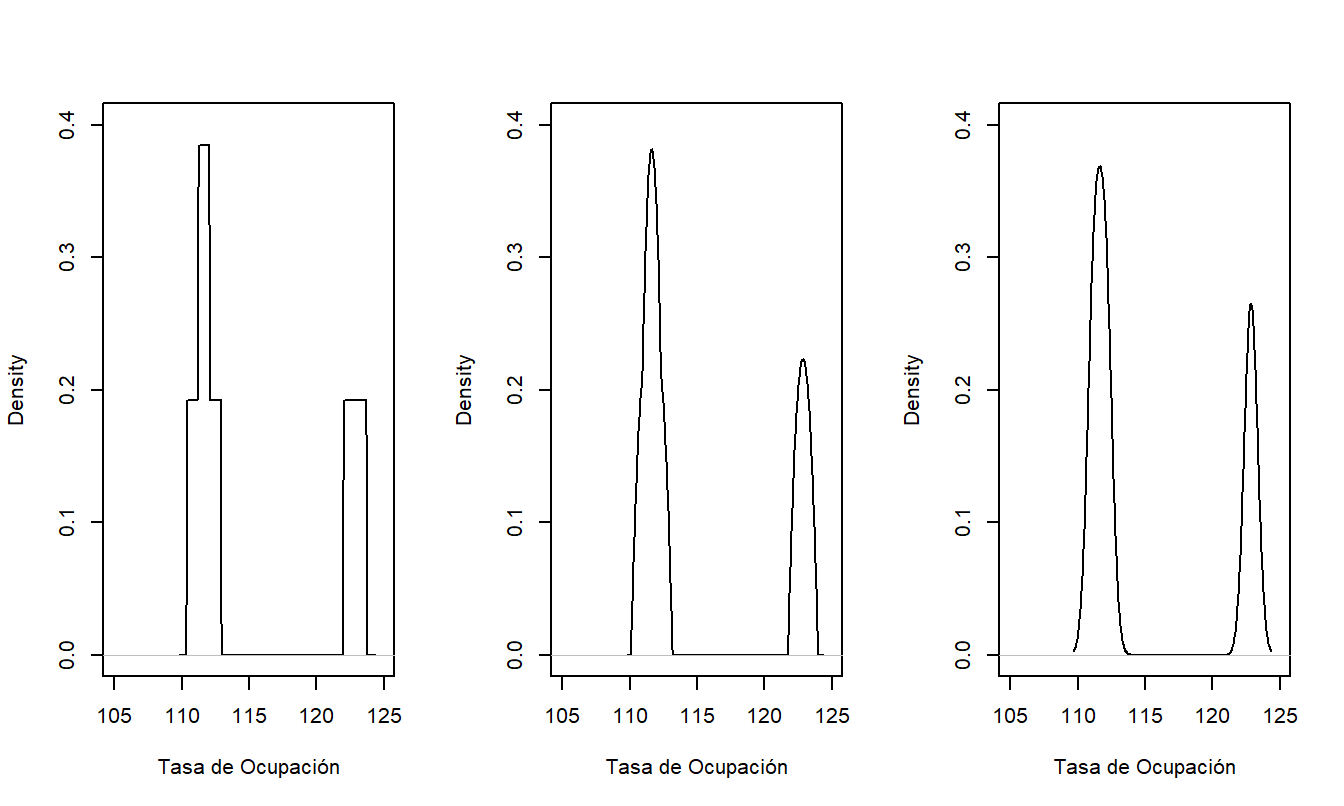
Figura 15.2: Estimaciones de Densidad con Núcleo de las Tasas de Ocupación de Hogares de Ancianos con Diferentes Núcleos. De izquierda a derecha, los paneles utilizan los núcleos uniforme, de Epanechnikov y gaussiano.
Código R para generar las Figuras 15.1 y 15.2
Algunos suavizadores de diagramas de dispersión que muestran relaciones entre un \(x\) y un \(y\), también pueden describirse en términos de estimación con núcleo. Específicamente, una estimación con núcleo de la función de regresión E(\(y|x\)) es \[ \hat{\mathrm{m}}(x) = \frac{\sum_{i=1}^n w_{i,x} y_i}{\sum_{i=1}^n w_{i,x}} \] con el peso “local” \(w_{i,x} = \mathrm{k}\left( (x_i - x)/b_n \right)\). Esta es la ahora clásica estimación de Nadaraya-Watson (ver, por ejemplo, Ruppert, Wand y Carroll, 2003).
Más generalmente, para un ajuste de polinomio local de orden \(p\), consideremos encontrar estimaciones de parámetros \(\beta_0, \ldots, \beta_p\) que minimicen \[\begin{equation} \sum_{i=1}^n \left\{ y_i - \beta_0 - \cdots - \beta_p (x_i - x)^p \right\}^2 w_{i,x}. \tag{15.17} \end{equation}\] El mejor valor de la intersección \(\beta_0\) se toma como la estimación de la función de regresión E(\(y|x\)). Ruppert, Wand y Carroll (2003) recomiendan valores de \(p=1\) o 2 para la mayoría de aplicaciones (la elección \(p=0\) produce la estimación de Nadaraya-Watson). Como una variación, al tomar \(p=1\) y permitir que el ancho de banda varíe para que el número de puntos utilizados para estimar la función de regresión sea fijo, se obtiene el estimador lowess (por “regresión local”) debido a Cleveland (ver, por ejemplo, Ruppert, Wand y Carroll, 2003). Como ejemplo, utilizamos el estimador lowess en la Figura 6.11 para tener una idea de la relación entre los residuos y el nivel de riesgo de una industria medida por INDCOST. Como analista, encontrará que los estimadores de densidad con núcleo y los suavizadores de diagramas de dispersión son bastante sencillos de usar al buscar patrones y desarrollar modelos.
15.4 Modelos Aditivos Generalizados
Los modelos lineales clásicos están basados en la función de regresión \[ \mu = \mathrm{E}(y| x_1, \ldots, x_k) = \beta_0 + \sum_{j=1}^k \beta_j x_j. \] Con un modelo lineal generalizado (GLM), hemos visto que podemos extender sustancialmente las aplicaciones mediante una función que vincula la media con el componente sistemático, \[ \mathrm{g} \left(\mu \right) = \beta_0 + \sum_{j=1}^k \beta_j x_j, \] desde la ecuación (13.1). Como en los modelos lineales, el componente sistemático es lineal en los parámetros \(\beta_j\), no necesariamente en las variables explicativas subyacentes. Por ejemplo, hemos visto que podemos usar funciones polinómicas (como \(x^2\) en el Capítulo 3), funciones trigonométricas (como \(\sin x\) en el Capítulo 8), variables binarias y categorizaciones en el Capítulo 4, y la representación de “palos rotos” (lineal por tramos) en la Sección 3.5.2.
El modelo aditivo generalizado (GAM) extiende el GLM al permitir que cada variable explicativa sea reemplazada por una función que puede ser no lineal, \[\begin{equation} \mathrm{g} \left( \mu \right) = \beta_0 + \sum_{j=1}^k \beta_j ~\mathrm{m}_j(x_j). \tag{15.18} \end{equation}\] Aquí, la función \(\mathrm{m}_j(\cdot)\) puede diferir según la variable explicativa. Dependiendo de la aplicación, \(\mathrm{m}_j(\cdot)\) puede incluir las especificaciones paramétricas tradicionales (como polinomios y categorizaciones) así como especificaciones no paramétricas más flexibles como los suavizadores de diagramas de dispersión introducidos en la Sección 15.3.
Por ejemplo, supongamos que tenemos una gran base de datos de seguros y deseamos modelar la probabilidad de un siniestro. Entonces, podríamos usar el modelo \[ \ln \left(\frac{\pi}{1-\pi} \right) = \beta_0 + \sum_{j=1}^k \beta_j x_j + \mathrm{m}(z). \] El lado izquierdo es la usual función de enlace logit utilizada en regresión logística, con \(\pi\) siendo la probabilidad de un siniestro. Para el lado derecho, podríamos considerar una serie de variables de calificación, como territorio, género y tipo de vehículo o casa (dependiendo de la cobertura), que están incluidas en el componente lineal \(\beta_0 + \sum_{j=1}^k \beta_j x_j\). La variable adicional \(z\) es una variable continua (como la edad) para la que deseamos permitir la posibilidad de efectos no lineales. Para la función \(\mathrm{m}(z)\), podríamos usar un ajuste polinómico de orden \(p\) con discontinuidades en varias edades, como en la ecuación (15.17).
Este es conocido como un modelo semiparamétrico, en el que el componente sistemático consta de partes paramétricas (\(\beta_0 + \sum_{j=1}^k \beta_j x_j\)) y no paramétricas (\(\mathrm{m}(z)\)). Aunque no presentamos los detalles aquí, el software estadístico moderno permite la estimación simultánea de los parámetros de ambos componentes. Por ejemplo, el software estadístico SAS implementa modelos aditivos generalizados en su procedimiento PROC GAM, al igual que el software R mediante el paquete VGAM.
La especificación del GAM en la ecuación (15.18) es bastante general. Para una clase más limitada, la elección de g(\(\cdot\)) como la función identidad produce el modelo aditivo. Aunque general, las formas no paramétricas de \(\mathrm{m}_j(\cdot)\) hacen que el modelo sea más flexible, pero la aditividad nos permite interpretar el modelo de manera similar a antes. Los lectores interesados en más información sobre los GAM encontrarán útiles los textos de Ruppert, Wand y Carroll (2003) y Hastie, Tibshirani y Freedman (2001).
15.5 Bootstrapping
El bootstrap es una herramienta general para evaluar la distribución de una estadística. Primero describimos el procedimiento general y luego discutimos formas de implementarlo en un contexto de regresión.
Supongamos que tenemos una muestra i.i.d. \(\{z_1, \ldots, z_n \}\) de una población. A partir de estos datos, deseamos entender la confiabilidad de una estadística \(\mathrm{S}(z_1, \ldots, z_n )\). Para calcular una distribución bootstrap, realizamos:
Muestra Bootstrap. Generar una muestra i.i.d. de tamaño \(n\), \(\{z^{\ast}_{1r}, \ldots, z^{\ast}_{nr} \}\), a partir de \(\{z_1, \ldots, z_n \}\).
Replicación Bootstrap. Calcular la replicación bootstrap, \(S^{\ast}_r =\mathrm{S}(z^{\ast}_{1r}, \ldots, z^{\ast}_{nr} )\).
Repetir los pasos (i) y (ii) \(r=1, \ldots, R\) veces, donde \(R\) es un gran número de replicaciones. En el primer paso, la muestra bootstrap se extrae aleatoriamente de la muestra original con reemplazo. Al repetir los pasos (i) y (ii), las muestras bootstrap son independientes entre sí, condicionado a la muestra original \(\{z_1, \ldots, z_n \}\). La distribución bootstrap resultante, \(\{S^{\ast}_1, \ldots, S^{\ast}_R\}\), puede usarse para evaluar la distribución de la estadística \(S\).
Existen tres variaciones de este procedimiento básico usadas en regresión. En la primera variación, tratamos \(z_i = (y_i, \mathbf{x}_i)\), y usamos el procedimiento básico bootstrap. Esta variación se conoce como remuestreo de pares.
En la segunda variación, tratamos los residuos de la regresión como la muestra “original” y creamos una muestra bootstrap remuestreando los residuos. Esta variación se conoce como remuestreo de residuos. Específicamente, consideremos un modelo de regresión genérico de la forma \(y_i = \mathrm{F}(\mathbf{x}_i, \boldsymbol \theta, \varepsilon_i),\) donde \(\boldsymbol \theta\) representa un vector de parámetros. Supongamos que estimamos este modelo y calculamos residuos \(e_i, i=1, \ldots, n\). En la Sección 13.5, denotamos los residuos como \(e_i = \mathrm{R}(y_i; \mathbf{x}_i,\widehat{\boldsymbol \theta})\) donde la función “R” fue determinada por la forma del modelo y \(\widehat{\boldsymbol \theta}\) representa el vector estimado de parámetros. Los residuos pueden ser los residuos crudos, residuos de Pearson u otra elección.
Usando un residuo bootstrap \(e^{\ast}_{jr}\), podemos crear una pseudo-respuesta \[ y^{\ast}_{jr}= \mathrm{F}(\mathbf{x}_i, \widehat{\boldsymbol \theta}, e^{\ast}_{jr}). \] Podemos entonces usar el conjunto de pseudo-observaciones \(\{(y^{\ast}_{1r},\mathbf{x}_1), \ldots, (y^{\ast}_{nr},\mathbf{x}_n)\}\) para calcular la replicación bootstrap \(S^{\ast}_r\). Como antes, la distribución bootstrap resultante, \(\{S^{\ast}_1, \ldots, S^{\ast}_R\}\), puede usarse para evaluar la distribución de la estadística \(S\).
Comparando estas dos opciones, las fortalezas de la primera variación son que emplea menos suposiciones y es más sencilla de interpretar. La limitación es que utiliza un conjunto diferente de variables explicativas \(\{\mathbf{x}^{\ast}_{1r}, \ldots, \mathbf{x}^{\ast}_{nr} \}\) en el cálculo de cada replicación bootstrap. Algunos analistas consideran que su inferencia sobre la estadística \(S\) está condicionada a las variables explicativas observadas \(\{\mathbf{x}_1, \ldots, \mathbf{x}_n \}\) y usar un conjunto diferente aborda un problema que no es de interés. La segunda variación aborda esto, pero a costa de una menor generalidad. En esta variación, hay una suposición más fuerte de que el analista ha identificado correctamente el modelo y que el proceso de perturbación \(\varepsilon_i = \mathrm{R}(y_i; \mathbf{x}_i,\boldsymbol \theta)\) es i.i.d.
La tercera variación se conoce como bootstrap paramétrico. Aquí, asumimos que las perturbaciones, y por lo tanto las variables dependientes originales, provienen de un modelo que se conoce hasta un vector de parámetros. Por ejemplo, supongamos que deseamos evaluar la precisión de una estadística \(S\) a partir de una regresión de Poisson. Como se describe en el Capítulo 12, asumimos que \(y_i \sim Poisson (\mu_i)\), donde \(\mu_i = \exp(\mathbf{x}_i^{\prime} \boldsymbol \beta )\). La estimación de los parámetros de regresión es \(\mathbf{b}\) y, por lo tanto, la media estimada es \(\widehat{\mu}_i = \exp(\mathbf{x}_i^{\prime} \mathbf{b} )\). A partir de esto, podemos simular para crear un conjunto de pseudo-respuestas \[ y^{\ast}_{ir}\sim Poisson (\widehat{\mu}_i), i=1,\ldots, n, ~~~r=1,\ldots, R. \] Estas pseudo-respuestas pueden usarse para formar la muestra bootstrap \(r\), \(\{(y^{\ast}_{1r},\mathbf{x}_1), \ldots, (y^{\ast}_{nr},\mathbf{x}_n)\}\), y a partir de esta la replicación bootstrap, \(S^{\ast}_r\). Así, la principal diferencia entre el bootstrap paramétrico y las dos primeras variaciones es que simulamos a partir de una distribución (Poisson, en este caso), no de una muestra empírica. El bootstrap paramétrico es fácil de interpretar y explicar porque el procedimiento es similar a la simulación de Monte Carlo habitual (ver, por ejemplo, Klugman et al., 2008). La diferencia es que con el bootstrap, usamos los parámetros estimados para calibrar la distribución de muestreo bootstrap, mientras que en la simulación de Monte Carlo esta distribución se asume conocida.
Hay dos formas comúnmente usadas para resumir la precisión de la estadística \(S\) utilizando la distribución bootstrap, \(\{S^{\ast}_1, \ldots, S^{\ast}_R\}\). La primera, un enfoque independiente del modelo, implica usar los percentiles de la distribución bootstrap para crear un intervalo de confianza para \(S\). Por ejemplo, podríamos usar los percentiles \(2.5^{th}\) y \(97.5^{th}\) de \(\{S^{\ast}_1, \ldots, S^{\ast}_R\}\) para un intervalo de confianza del 95% para \(S\). En el segundo, se asume alguna distribución para \(S^{\ast}_r,\) típicamente una normalidad aproximada. Con este enfoque, se puede estimar una media y una desviación estándar para obtener el intervalo de confianza usual para \(S\).
Caso Especial: Bootstrap para Reservas de Pérdidas. England y Verrall (2002) discuten el uso de bootstrap para reservas de pérdidas. Como veremos en el Capítulo 19, al asumir que las pérdidas siguen un modelo Poisson sobredisperso, se pueden obtener predicciones para las reservas de pérdidas mediante un procedimiento mecánico simple conocido como la técnica chain-ladder. Para realizar un bootstrap de un modelo Poisson sobredisperso, como vimos en el Capítulo 12, esto es una variación de un modelo Poisson, no una verdadera distribución de probabilidad, y por lo tanto, el bootstrap paramétrico no está fácilmente disponible. En su lugar, England y Verrall mostraron cómo usar remuestreo de residuos, empleando residuos de Pearson.
En muchos casos, el cálculo de la replicación bootstrap \(S^{\ast}_r\) de la estadística puede ser computacionalmente intensivo, requiriendo software especializado. Sin embargo, como señalaron England y Verrall, el caso de reservas de pérdidas con un modelo Poisson sobredisperso es sencillo. Básicamente, se utiliza la técnica chain-ladder para estimar los parámetros del modelo y calcular los residuos de Pearson. Luego, se simula a partir de los residuos, se crean pseudo-respuestas y distribuciones bootstrap. Debido a que la simulación está ampliamente disponible, todo el procedimiento se puede mecanizar fácilmente para trabajar con paquetes de hojas de cálculo estándar, sin necesidad de software estadístico. Véase el Apéndice 3 de England y Verrall (2002) para más detalles sobre el algoritmo.
15.6 Lecturas Adicionales y Referencias
La fórmula en las ecuaciones (15.10) no considera la incertidumbre en la estimación de los componentes de varianza. Se han propuesto factores de inflación que consideran esta incertidumbre adicional (Kackar y Harville, 1984), pero tienden a ser pequeños, al menos para conjuntos de datos comúnmente encontrados en la práctica. McCulloch y Searle (2001) ofrecen discusiones adicionales.
Silverman (1986) es una introducción clásica a la estimación de densidad.
Ruppert, Wand y Carroll (2003) proporcionan un excelente libro de introducción al suavizado de gráficos de dispersión. Además, ofrecen una discusión completa sobre suavizadores basados en splines, una alternativa al ajuste polinómico local.
Efron y Tibshirani (1991) es una introducción clásica al bootstrap.
Referencias
- Efron, Bradley and Robert Tibshirani (1991). An Introduction to the Bootstrap. Chapman and Hall, London.
- England, Peter D. and Richard J. Verrall (2002). Stochastic claims reserving in general insurance. British Actuarial Journal 8, 443-544.
- Frees, Edward W. (2004). Longitudinal and Panel Data: Analysis and Applications in the Social Sciences. Cambridge University Press, New York.
- Frees, Edward W., Virginia R. Young and Yu Luo (2001). Case studies using panel data models. North American Actuarial Journal 5 (4), 24-42.
- Gelman, A., J. B. Carlin, H. S. Stern and D. B. Rubin (2004). Bayesian Data Analysis, Second Edition. Chapman & Hall, New York.
- Goldberger, Arthur S. (1962). Best linear unbiased prediction in the generalized linear regression model. Journal of the American Statistical Association 57, 369-75.
- Hastie, Trevor, Robert Tibshirani and Jerome Friedman (2001). The Elements of Statistical Learning: Data Mining, Inference and Prediction. Springer, New York.
- Henderson, C. R. (1973), Sire evaluation and genetic trends, in Proceedings of the Animal Breeding and Genetics Symposium in Honor of Dr. Jay L. Lush, 10-41. Amer. Soc. Animal Sci.-Amer. Dairy Sci. Assn. Poultry Sci. Assn., Champaign, Illinois.
- Kackar, R. N. and D. Harville (1984). Approximations for standard errors of estimators of fixed and random effects in mixed linear models. Journal of the American Statistical Association 79, 853-862.
- Klugman, Stuart A, Harry H. Panjer and Gordon E. Willmot (2008). Loss Models: From Data to Decisions. John Wiley & Sons, Hoboken, New Jersey.
- McCulloch, Charles E. and Shayle R. Searle (2001). Generalized, Linear and Mixed Models. John Wiley & Sons, New York.
- Pinheiro, José C. and Douglas M. Bates (2000). Mixed-Effects Models in S and S-PLUS. Springer-Verlag, New York.
- Ruppert, David, M.P. Wand and Raymond J. Carroll (2003). Semiparametric Regression. Cambridge University Press, Cambridge.
- Silverman, B. W. (1986). Density Estimation for Statistics and Data Analysis. Chapman and Hall, London.