Capítulo 21 Diseñando Gráficos Efectivos
Vista Previa del Capítulo.1 Los actuarios, como otros profesionales de negocios, comunican ideas cuantitativas mediante gráficos. Dado que el proceso de leer, o decodificar, gráficos es más complejo que leer texto, los gráficos son vulnerables al abuso. Para resaltar esta vulnerabilidad, damos varios ejemplos de gráficos comúnmente encontrados que inducen a error y ocultan información. Para ayudar a los creadores a diseñar gráficos más efectivos y a los espectadores a reconocer gráficos engañosos, este capítulo resume pautas para diseñar gráficos que muestren información numérica importante. Al diseñar gráficos, los creadores deben:
- Evitar “chartjunk” (elementos gráficos innecesarios).
- Usar pequeños múltiples para promover comparaciones y evaluar cambios.
- Usar gráficos complejos para representar patrones complejos.
- Relacionar el tamaño del gráfico con el contenido de información.
- Usar formas gráficas que promuevan comparaciones.
- Integrar gráficos y texto.
- Demostrar un mensaje importante.
- Conocer a la audiencia.
Algunas de estas pautas para diseñar gráficos efectivos, como (6), (7) y (8), se derivan directamente de principios para una escritura efectiva. Otras, como las pautas (3), (4) y (5), provienen de la psicología cognitiva, la ciencia de la percepción. Las pautas (1) y (2) tienen raíces tanto en la escritura efectiva como en la percepción gráfica. Por ejemplo, el principio de brevedad en la escritura demuestra cómo la eliminación de perspectivas tridimensionales pseudo y otras formas de “chartjunk” mejora los gráficos. Como otro ejemplo, el principio de estructura paralela en la escritura sugiere usar pequeñas variaciones múltiples de una forma gráfica básica para visualizar relaciones complejas entre diferentes grupos y a lo largo del tiempo.
Para resaltar el aspecto científico de la percepción gráfica, examinamos el proceso de comunicación con un gráfico, comenzando con la interpretación de los datos por parte del emisor y terminando con la interpretación del gráfico por parte del receptor. En consonancia con la tradición científica, este capítulo discute varios estudios en la literatura sobre la efectividad de los gráficos.
Concluimos que la profesión actuarial tiene muchas oportunidades para mejorar su práctica, haciendo la comunicación más eficiente y precisa.
21.1 Introducción
Al igual que otros profesionales de negocios, los actuarios comunican ideas de manera oral y escrita, así como a través de presentaciones, que son formas interactivas de comunicación que abarcan mensajes orales y escritos. Los actuarios, así como otros analistas financieros, comunican ideas con componentes cuantitativos importantes. Los escritores expresan ideas cuantitativas como (1) números dentro de párrafos, (2) números dentro de formas tabulares, (3) relaciones funcionales como ecuaciones, y (4) datos o ecuaciones como gráficos.
Los gráficos son un medio simple pero poderoso para la comunicación escrita de ideas cuantitativas. Los gráficos pueden presentar una gran cantidad de datos en un espacio pequeño, expresar relaciones importantes entre cantidades, comparar diferentes conjuntos de datos y describir datos, proporcionando así una imagen coherente de sistemas complejos. Los gráficos hacen más que simplemente declarar una idea; la demuestran.
Los gráficos son poderosos porque son flexibles, pero esa flexibilidad puede ser una desventaja debido al potencial de abuso. Las referencias bien aceptadas que tratan métodos de presentación de datos cuantitativos mitigan las oportunidades de abuso. El Chicago Manual of Style (1993), una referencia estándar, discute la presentación de datos dentro del texto, y Ehrenberg (1977) y Tufte (1983) discuten la presentación de datos tabulares. En contraste, nos enfocamos en la presentación de datos a través de exhibiciones gráficas.
Este capítulo busca mejorar la práctica actuarial en lo que respecta a exhibiciones gráficas. Pretendemos: (1) demostrar la importancia de las exhibiciones gráficas, (2) proporcionar pautas para mejorar la práctica gráfica, y (3) introducir algunos fundamentos científicos de la buena práctica gráfica. La agenda es ambiciosa, pero el objetivo de este capítulo es proporcionar a los actuarios practicantes herramientas básicas que puedan usar para convertirse en consumidores críticos y productores efectivos de gráficos. También esperamos que los lectores adopten nuestro entusiasmo y deseen explorar por su cuenta la literatura sobre diseño gráfico.
Un tema importante de este capítulo es que los principios de la escritura vigorosa pueden y deben aplicarse a la práctica de hacer gráficos efectivos. El Elements of Style (Strunk y White 1979, p. xiv) resume la escritura vigorosa:
La escritura vigorosa es concisa. Una oración debe contener solo las palabras necesarias, un párrafo solo las oraciones necesarias, por la misma razón que un dibujo no debe tener líneas innecesarias y una máquina no debe tener piezas innecesarias. Esto no requiere que el escritor haga todas sus oraciones cortas, o que evite todo detalle y trate sus temas solo en esquema, sino que cada palabra cuente.
White atribuye esta cita a William Strunk. White la llama “un ensayo breve y valioso sobre la naturaleza y la belleza de la brevedad – sesenta y tres palabras que podrían cambiar el mundo.” Argumentamos que la brevedad es especialmente importante al crear gráficos efectivos. Esto también fue entendido por Strunk; como se señaló anteriormente, dijo “un dibujo no debe contener líneas innecesarias …” Usamos el término chartjunk, introducido por Tufte (1983), para cualquier elemento innecesario en un gráfico.
Los principios de escritura vigorosa, además de la brevedad, también se aplican a la práctica de crear gráficos efectivos. Al igual que en la escritura, los gráficos efectivos son el resultado de revisiones y ediciones repetidas. Los gráficos mal diseñados pueden ocultar información y confundir. Los gráficos extravagantes o pretenciosos son una distracción cuando gráficos más simples son suficientes.
Aunque los principios de escritura efectiva son valiosos, no son suficientes para producir gráficos efectivos. La escritura se procesa de manera secuencial, palabra por palabra, oración por oración, con un principio y un final. El proceso de “leer,” o decodificar, un gráfico es no lineal y más complejo. Estas complejidades adicionales significan que incluso los autores que siguen prácticas efectivas de escritura pueden producir gráficos ineficaces. A menudo, la forma de la prosa escrita es el único determinante de su valor, mientras que en los gráficos el proceso de comunicación desempeña el papel dominante. Asumimos que los lectores están familiarizados con las formas efectivas de escritura. Por lo tanto, primero revisamos el proceso de comunicación en el que un gráfico juega un papel crucial.
Para subrayar la importancia de un diseño gráfico efectivo, la Sección 21.2 proporciona varias ilustraciones de gráficos que ocultan información y confunden; los defectos ilustrados son inconvenientes más serios que simples chartjunk. Las ilustraciones de la Sección 21.2 motivan la necesidad de pautas adicionales y métodos para construir gráficos efectivos.
La Sección 21.3 introduce ocho pautas importantes para crear y visualizar gráficos. Aunque estas pautas no son una panacea para todos los defectos gráficos, sí proporcionan a los profesionales de negocios, como los actuarios, una lista clave para crear gráficos efectivos. Las pautas están organizadas de modo que las dos primeras, sobre chartjunk y el uso de múltiples, se basan tanto en perspectivas de escritura efectiva como en la percepción gráfica. Las pautas Tres, Cuatro y Cinco están relacionadas principalmente con la literatura de percepción gráfica, mientras que las pautas Seis, Siete y Ocho se basan principalmente en principios de escritura efectiva.
Al igual que en la escritura efectiva, las cuestiones de estilo entran en la discusión de lo que es y lo que no es un gráfico efectivo. Muchas decisiones de estilo se basan en prácticas aceptadas sin una base científica firme. Sin embargo, el proceso de percibir gráficos ha sido objeto de estudio en varias disciplinas científicas, incluidas la psicofísica, la psicología cognitiva y las visiones computacionales (Cleveland 1995, Capítulo 4). La Sección 21.4 ilustra algunos tipos de evidencia experimental para determinar una forma gráfica efectiva basada tanto en el receptor como en el gráfico como unidades de estudio. La Sección 21.4 también muestra cómo algunos gráficos comunes en publicaciones de negocios, como los gráficos de barras y de pastel, son malos comunicadores de información numérica.
Las Secciones 21.5 y 21.6 contienen observaciones finales y descripciones de algunos recursos para actuarios que deseen aprender más sobre cómo diseñar gráficos efectivos.
La mayoría de los lectores están alejados de los datos detallados resumidos por un gráfico. Varias dificultades y conceptos erróneos pueden surgir debido a la distancia entre los datos originales y la interpretación del gráfico por parte del espectador. La Figura 21.1 ilustra el desafío de comunicarse con un gráfico. El emisor (y creador) del gráfico tiene un mensaje derivado de una interpretación de datos. Aunque algunos gráficos comunican datos en bruto, el propósito principal de la mayoría de los gráficos es comunicar la interpretación del emisor. El mensaje que el emisor pretende se codifica en un gráfico y se transmite al receptor.
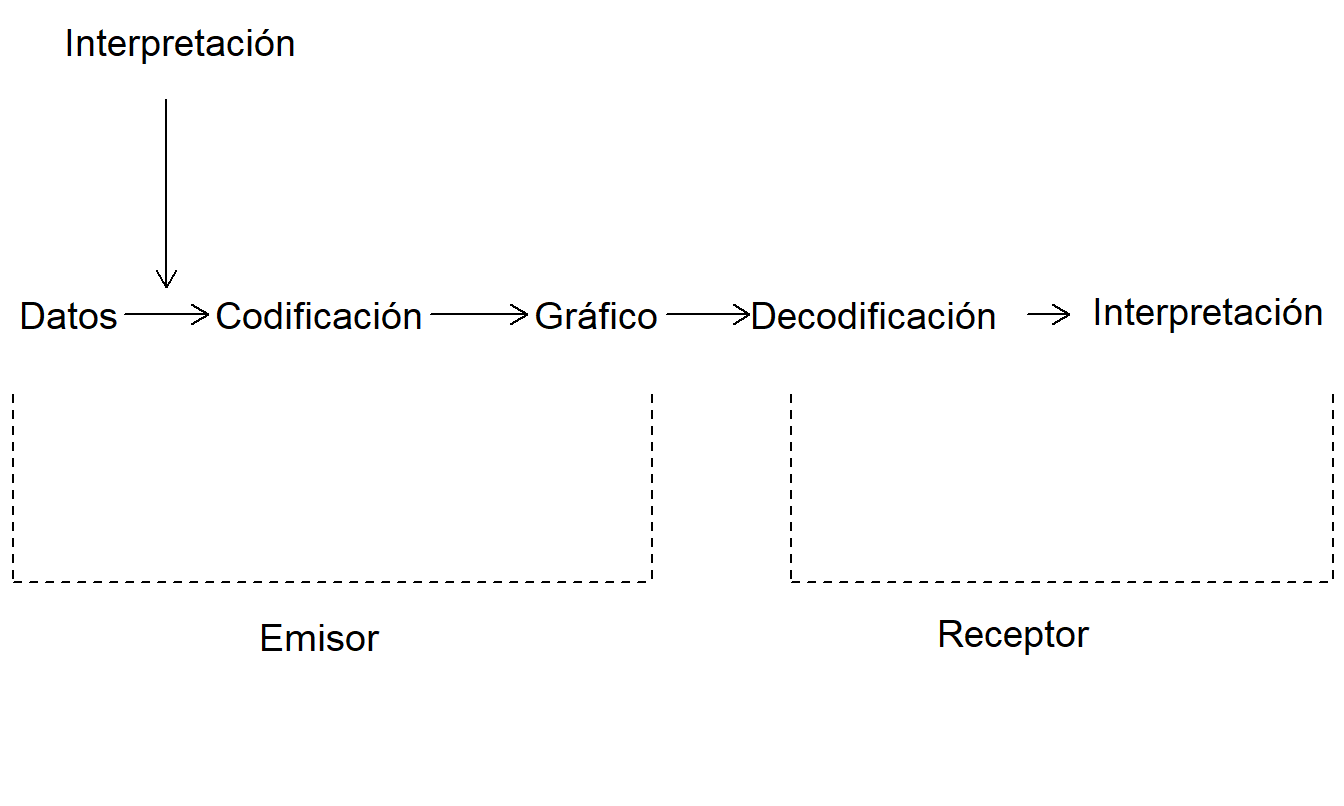
Figura 21.1: Diagrama de flujo del proceso de comunicación con un gráfico. El gráfico es un intermediario crucial en el proceso de comunicar la interpretación de los datos al receptor.
En general, el receptor no está involucrado ni con la interpretación exacta pretendida por el emisor ni con los datos originales. Por lo tanto, el receptor debe decodificar el gráfico y desarrollar una interpretación de su mensaje. Surgen dos cuestiones:
- ¿La interpretación construida por el receptor es congruente con la interpretación del emisor?
- ¿La interpretación del receptor es consistente y está respaldada por los datos?
El primer tema depende de la habilidad con la que el emisor construye el gráfico y de la habilidad con la que el receptor lo decodifica. Un gráfico mal diseñado puede ocultar o distorsionar el mensaje del emisor. Un gráfico difícil de leer puede desalentar al receptor de dedicar el tiempo necesario para decodificar el mensaje correctamente. El receptor puede ignorar o malinterpretar un gráfico que no está construido con cuidado.
El segundo tema depende no solo de las habilidades mencionadas anteriormente, sino también de la habilidad con la que el emisor extrae significado de los datos. ¿Qué tan cuidadosamente documenta el emisor el proceso de interpretación? ¿Esto se comunica al receptor? ¿Es el receptor capaz de evaluar hasta qué punto el gráfico es un resumen creíble de los datos? El fallo en cualquiera de estos puntos podría resultar en que el receptor ignore o malinterprete el gráfico.
Este capítulo asume que los gráficos incluidos en comunicaciones empresariales son objeto de escrutinio por lectores serios. Los gráficos que aparecen rápidamente en la pantalla de televisión, un rotafolio o un paquete de presentaciones están diseñados para atraer la atención y entretener al espectador. En estos medios, predominan las consideraciones de diseño sobre la información. Nos centramos, en cambio, en gráficos que forman parte de la escritura profesional y están diseñados para informar. Al igual que con la escritura efectiva, asumimos que al crear gráficos “uno debe creer… en la verdad y el valor del boceto, en la capacidad del lector para recibir y decodificar el mensaje” (Strunk y White 1979, p. 84). Ahora pasamos a ejemplos de gráficos que engañan.
21.2 Las Elecciones de Diseño Gráfico Marcan la Diferencia
Como señaló Schmid (1992), el antiguo proverbio “Una imagen vale más que mil palabras,” cuando se aplica a los gráficos podría leerse como “Una imagen puede valer más que mil palabras o cifras.” El potencial gráfico no se realiza fácilmente. Debido a su flexibilidad, los gráficos con demasiada frecuencia muestran representaciones visuales de información cuantitativa que son poco informativas, confusas o incluso engañosas.
Los ejemplos 21.2.1 a 21.2.5 ilustran cinco tipos diferentes de gráficos engañosos. En cada caso, los datos no se alteraron ni se representaron diferentes dimensiones de los datos. El tema común de los ejemplos es que, al alterar únicamente las escalas de los datos, el creador puede cambiar drásticamente la interpretación del espectador.
Ejemplo 21.2.1: Incluir el cero para comprimir datos2. La Figura 21.2 muestra una serie temporal del porcentaje de trabajadores equivalentes a tiempo completo empleados en la industria de seguros. Los datos anuales, 1948-1993, provienen de las Cuentas Nacionales de Ingreso y Producto producidas por la Oficina de Estadísticas Laborales. El panel izquierdo, Figura 21.2(a), da la impresión de un entorno de empleo estable para la industria de seguros. Incluir el cero en el eje vertical produce esta aparente estabilidad. Al hacer esto, la mayor parte del gráfico se dedica al espacio en blanco que no muestra la variabilidad en los datos. En contraste, el panel derecho, Figura 21.2(b), utiliza los datos para establecer el rango en los ejes. Este panel muestra claramente los grandes aumentos de empleo en los años posteriores a la Guerra de Corea, alrededor de 1952. También permite al lector ver las disminuciones de empleo que la industria de seguros ha sufrido en los últimos tres años.
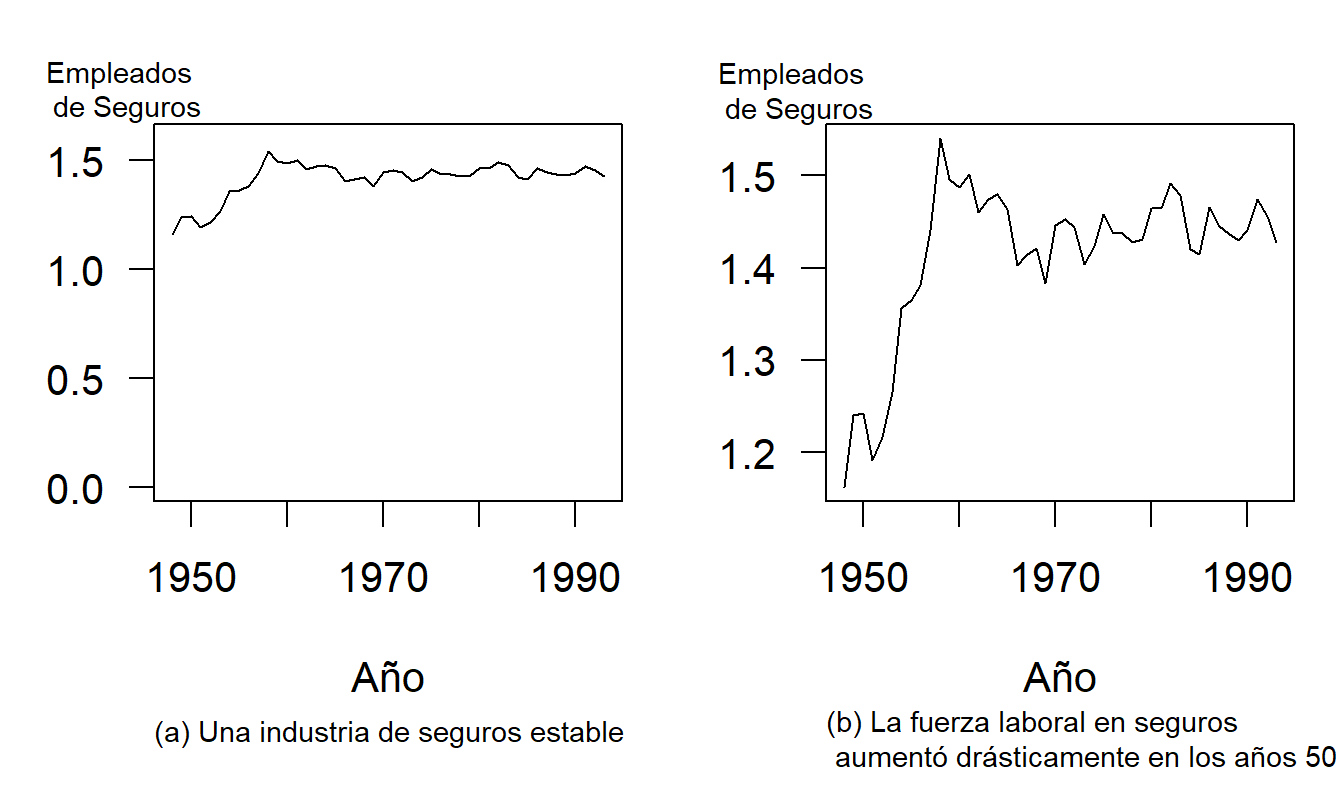
Figura 21.2: Empleados anuales en seguros, 1948-1993. ‘Empleados de seguros’ es el porcentaje de empleados equivalentes a tiempo completo que trabajan para aseguradoras. Permitir que los datos determinen los rangos de escala revela aspectos interesantes de los datos.
Código R para Generar la Figura 21.2
Este ejemplo es similar a una ilustración popular del conocido libro de Huff, How to Lie with Statistics (Huff 1954). El punto es que la motivación externa a los datos, como incluir el cero en un eje, puede invitarnos a alterar la escala de los datos y cambiar la interpretación que tiene el espectador de los mismos. Como muestra el Ejemplo 21.2.2, los creadores de gráficos también pueden alterar la interpretación del espectador cambiando ambas escalas en un gráfico bidimensional.
Ejemplo 21.2.2: Percepción de la Correlación. La Figura 21.3 relaciona la rentabilidad del manejo de riesgos con el tamaño de la empresa. Estos datos provienen de una encuesta a 73 gerentes de riesgo de grandes empresas internacionales con sede en los EE. UU., originalmente reportada en Schmit y Roth (1990). Los datos se analizan en la Sección 6.5. Aquí, la medida de la rentabilidad del manejo de riesgos, Firm Cost, se define como el logaritmo de las primas totales de propiedad y accidentes, más las pérdidas no aseguradas, como porcentaje de los activos totales de la empresa. La medida del tamaño de la empresa es el logaritmo de los activos totales.
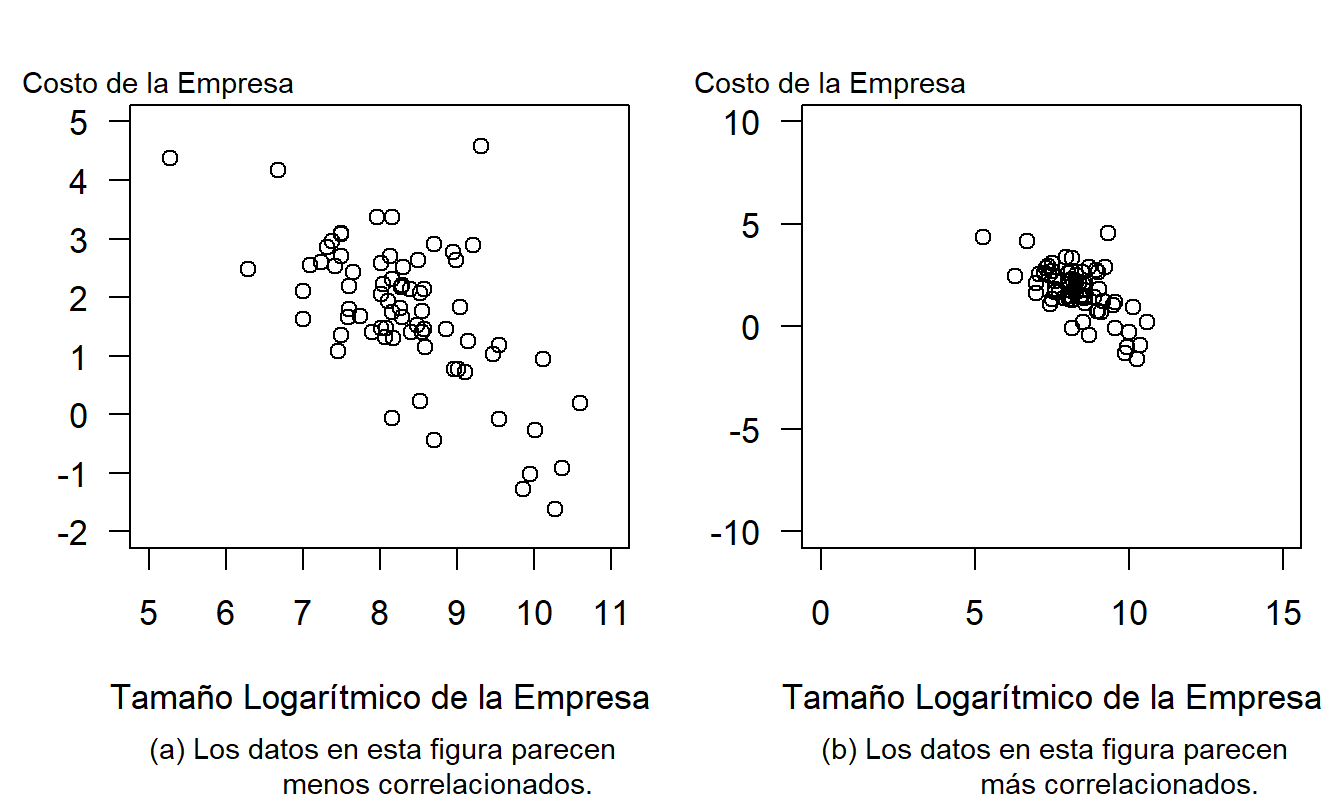
Figura 21.3: Eficiencia del Manejo de Riesgos versus Tamaño de la Empresa. Los datos representados en cada figura son los mismos. Sin embargo, las escalas más amplias en el panel (b) sugieren que los datos están más correlacionados.
Código R para Generar la Figura 21.3
El panel izquierdo, Figura 21.3(a), muestra una relación negativa entre los costos de la empresa y su tamaño, como anticiparon Schmit y Roth. El coeficiente de correlación entre las dos variables es -0.64. Los datos se encuentran en una porción central más pequeña de la Figura 21.3(b) en comparación con el panel izquierdo, Figura 21.3(a). La Figura 21.3(a) utiliza los datos para determinar los ejes y, por lo tanto, muestra más patrones en los datos. Como muestran Cleveland, Diaconis y McGill (1982), la escala hace que los datos en el panel derecho parezcan más correlacionados que en el panel izquierdo.
El cambio de escalas también puede alterar la percepción del espectador sobre las tendencias en los datos de series temporales, como se ilustra en el Ejemplo 21.2.3.
Ejemplo 21.2.3: Transformación a una Escala Logarítmica.
La Figura 21.4 muestra una serie temporal del mercado de seguros de crédito en los EE. UU. durante 1950-1989. Estos datos se analizan en Frees (1996) y provienen originalmente del Life Insurance Fact Book (1990). Cuando se examina el monto del seguro en una escala lineal en la Figura 21.4(a), el mercado de seguros de crédito parece estar expandiéndose rápidamente. Sin embargo, la Figura 21.4(b) muestra que, cuando se examina en una escala logarítmica, el mercado se está estabilizando. Como se discute en la Sección 3.2.2, los cambios en una escala logarítmica pueden interpretarse como cambios proporcionales. Así, la Figura 21.4(a) muestra que el mercado está aumentando rápidamente, y la Figura 21.4(b) muestra que la tasa de aumento se está estabilizando. Estos mensajes no son contradictorios, pero los espectadores deben interpretar cada gráfico críticamente para entender el mensaje pretendido.
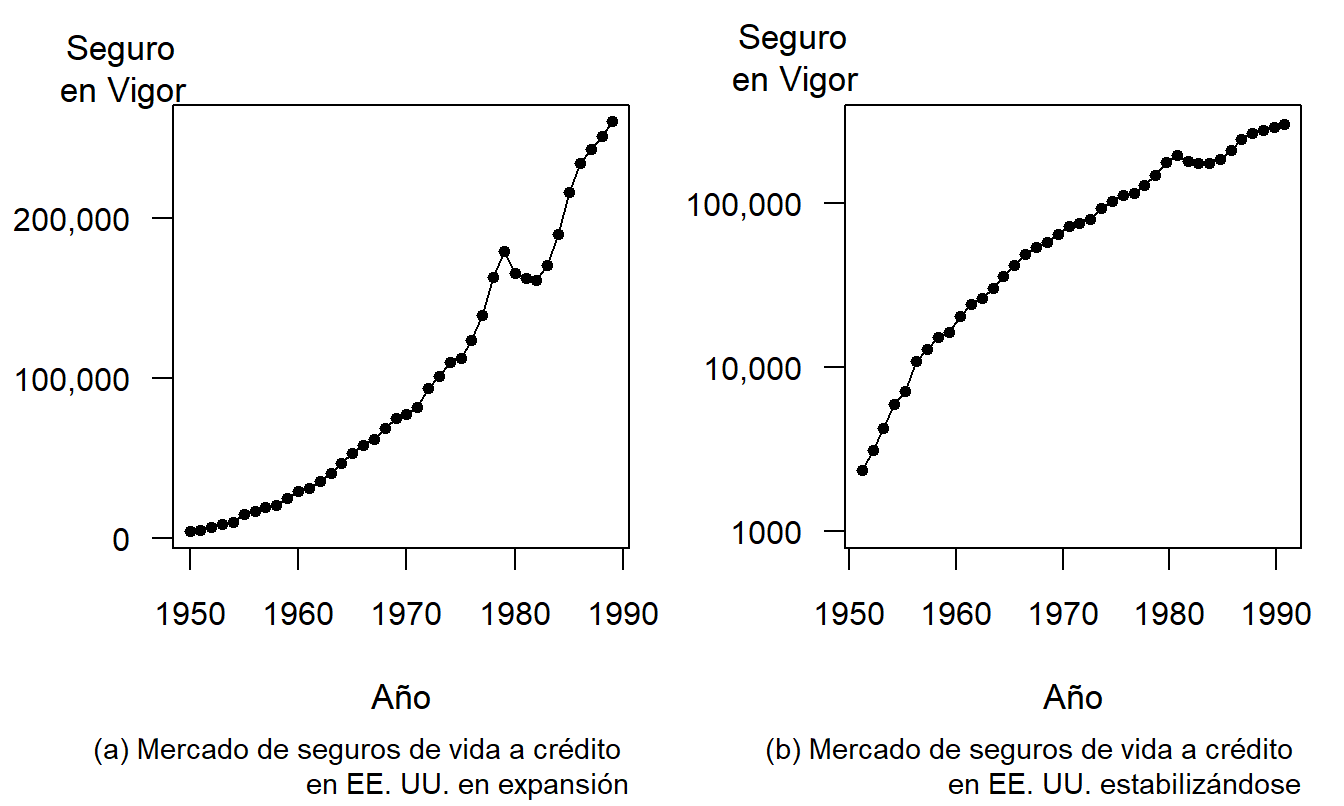
Figura 21.4: Seguro de Vida a Crédito Anual en los EE. UU., 1950-1989. Diferentes escalas verticales dan diferentes impresiones sobre la tasa de crecimiento a lo largo del tiempo.
Código R para Generar la Figura 21.4
Ejemplo 21.2.4: Doble Eje Y.
La Figura 21.5 muestra dos medidas de inflación producidas por la Oficina de Estadísticas Laborales. En el eje izquierdo se encuentra CPI_U, el índice de precios al consumidor para consumidores urbanos. En el eje derecho se encuentra CPI_M, el componente médico del índice general. Cada serie consta de valores mensuales que abarcan desde enero de 1947 hasta abril de 1995.
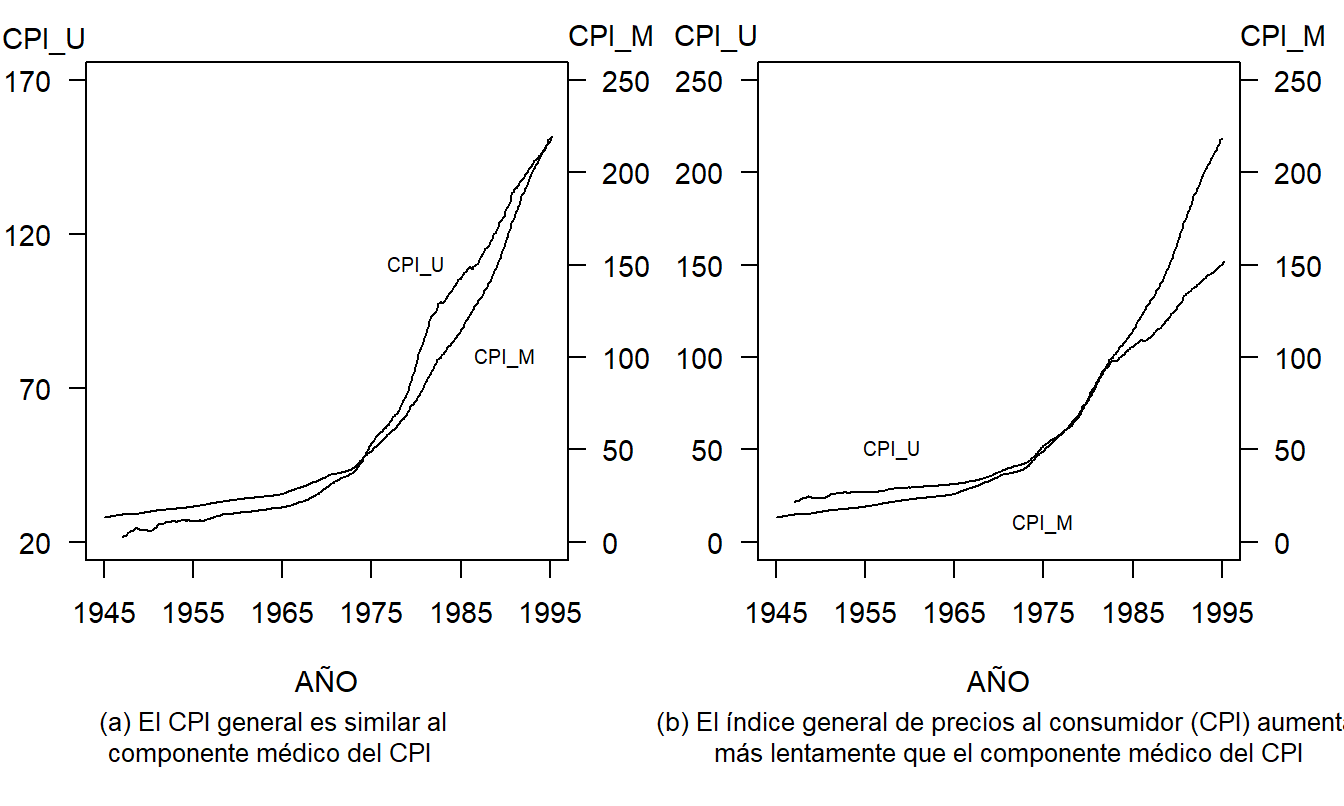
Figura 21.5: Valores Mensuales del Índice General de Precios al Consumidor (CPI) y del Componente Médico del CPI, enero de 1947 a abril de 1995. Diferentes rangos de escala alteran las apariencias de crecimiento relativo de las dos series.
Código R para Generar la Figura 21.5
El panel izquierdo, Figura 21.5(a), sugiere que el CPI_U y el CPI_M comienzan y terminan aproximadamente en la misma posición, lo que implica que han aumentado a tasas similares durante el período. El creador podría argumentar que cada índice mide el valor de un conjunto estándar de bienes, justificando el uso de una escala diferente para cada serie.
El panel derecho, Figura 21.5(b), proporciona una representación más útil de los datos al usar la misma escala para cada serie. Aquí, el CPI_M comienza más bajo que el CPI_U y termina más alto. Es decir, el índice del componente médico ha aumentado más rápidamente que el índice de precios para consumidores urbanos. También son evidentes otros patrones en la Figura 21.5: cada serie aumentó a una tasa similar entre 1979-1983, y el CPI_M aumentó mucho más rápidamente de 1983 a 1994 en comparación con 1948-1979.
Ejemplo 21.2.5: Relación de Aspecto.
La Figura 21.6 muestra una serie temporal de la tasa de desempleo mensual desde abril de 1953 hasta diciembre de 1992. La tasa de desempleo es el porcentaje de la fuerza laboral civil desempleada, ajustada estacionalmente. Es parte de la Encuesta de Hogares producida por la Oficina de Estadísticas Laborales, Departamento de Trabajo. Esta serie fue analizada en Frees et al. (1997). El panel superior de la Figura 21.6 muestra que la tasa de desempleo promedió un 5.9%, alcanzando un máximo de 10.8% en el cuarto trimestre de 1982 y un mínimo de 2.7% en el tercer trimestre de 1953.
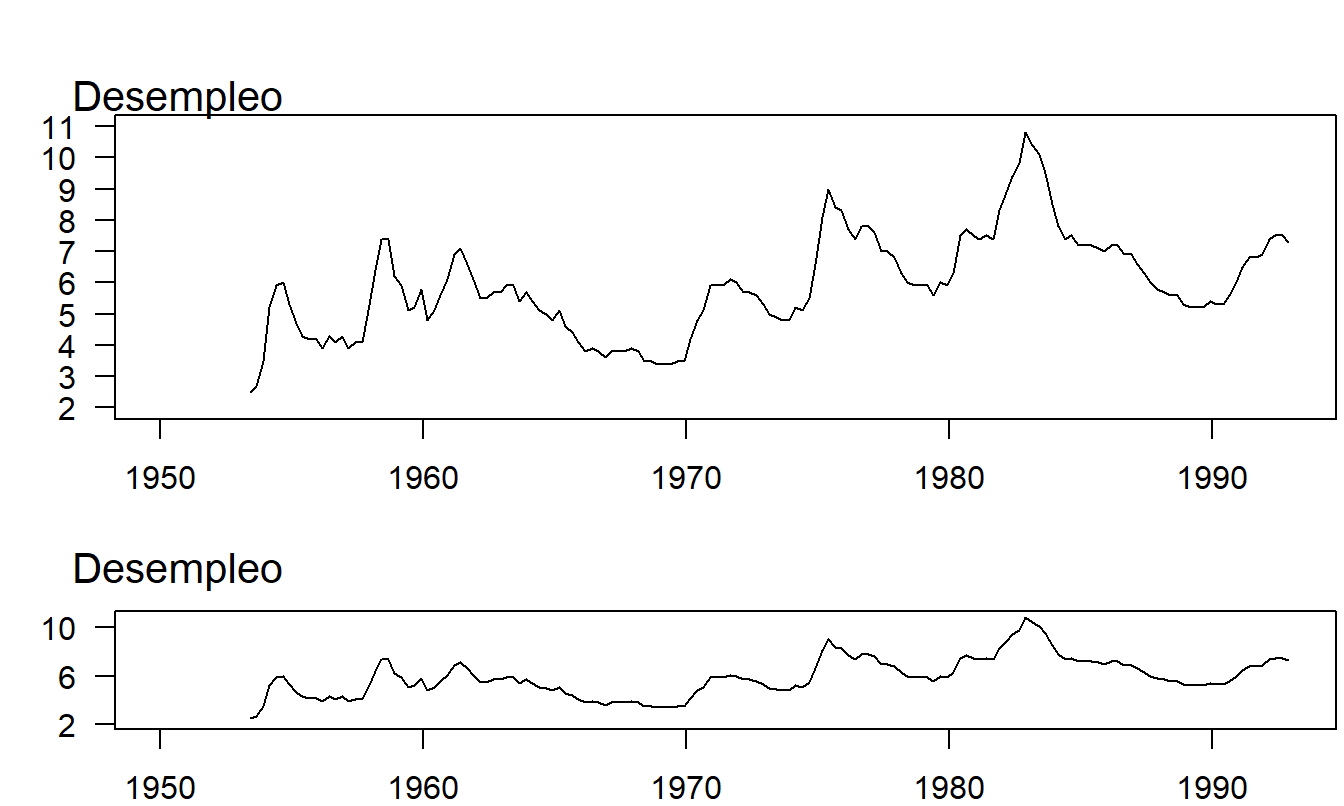
Figura 21.6: Gráfico de Series Temporales de Valores Trimestrales de la Tasa de Desempleo en EE.UU., 1953-1992. El panel inferior muestra una característica que no es evidente en el panel superior; el desempleo disminuye más lentamente de lo que aumenta.
Código R para Generar la Figura 21.6
Los dos paneles en la Figura 21.6 difieren solo en su forma, no en la escala de ninguna variable ni en la cantidad relativa de espacio que ocupan los datos dentro del marco de la figura. Para diferenciar estas dos formas, podemos usar el concepto de relación de aspecto de una figura, definida como la altura del marco de datos dividida por su ancho (algunas fuentes usan el recíproco de este valor para la relación de aspecto). El marco de datos es simplemente un rectángulo cuya altura y ancho permiten que el gráfico de los datos encaje dentro. Para ilustrar, en el panel superior de la Figura 21.6, la longitud del lado vertical es igual a la del lado horizontal. En el panel inferior, el lado vertical es solo el 25% del lado horizontal.
Ambos paneles muestran que la serie de desempleo osciló ampliamente durante este período de 39 años. Sin embargo, el panel inferior muestra una característica que no es evidente en el panel superior: el aumento hacia el pico de un ciclo de desempleo es más pronunciado que el descenso desde el pico. Dentro de cada ciclo de desempleo, el porcentaje de trabajadores desempleados tiende a aumentar rápidamente hasta un máximo y luego disminuir gradualmente hasta un mínimo. Este comportamiento es sorprendentemente regular durante el período de casi 39 años mostrado en el gráfico.
Relaciones de aspecto diferentes pueden dejar impresiones sustancialmente diferentes en el ojo, como ilustra la Figura 21.6. Por lo tanto, la relación de aspecto puede elegirse para enfatizar diferentes características de los datos.
21.3 Directrices de Diseño
Comprender los problemas ilustrados en la Sección 21.2 puede ayudar a los actuarios y otros profesionales de negocios a crear e interpretar gráficos. Esta sección presenta ocho directrices para diseñar gráficos efectivos. Uno de nuestros puntos principales es que la práctica actual no está en concordancia con estas directrices. Por lo tanto, anticipamos que no todos nuestros lectores encontrarán las demostraciones de las directrices visualmente atractivas, pero, como se mencionó en la Sección 21.1, muchas de las directrices se basan en una base científica descrita en la Sección 21.4. La “intuición” es algo que aprendemos y cultivamos; el progreso en la ciencia no siempre se conforma con la intuición actual. En un momento se creía ampliamente que la tierra era plana y que el sol giraba alrededor de la tierra. Las demostraciones de esta sección pueden o no ser inmediatamente intuitivas, pero son conclusiones lógicas de las directrices de diseño aquí defendidas.
Directriz Uno: Evitar Chartjunk
En la Sección 21.1, definimos chartjunk como cualquier adorno innecesario en un gráfico. Los creadores de gráficos que usan chartjunk reducen su credibilidad con receptores serios. Incluso cuando los emisores transmiten una interpretación correcta acompañada de chartjunk, piden a los receptores que procesen e ignoren correctamente el chartjunk. Si el chartjunk es parte de las opciones predeterminadas, o de fácil uso, de un paquete de software, el emisor puede sobrecargar un gráfico, o incluso hacerlo engañoso, simplemente presionando un botón.
Los emisores que evitan el chartjunk aumentan su credibilidad. Piden a los receptores que miren solo los caracteres y marcas significativos. Los emisores pueden tener que dedicar un tiempo considerable a su software para hacer gráficos efectivos, pero el respeto y la atención de sus receptores los recompensan. Otra forma de evitar el chartjunk es no usar un gráfico si unas pocas palabras bastarán. Si el mensaje de un gráfico puede resumirse en pocas palabras, entonces el gráfico no es necesario. ¡Evite imágenes que no valen diez mil palabras!
Evitar el chartjunk se basa en parte en el concepto de brevedad en los principios de escritura vigorosa. Desde el punto de vista de la percepción gráfica, evitar el chartjunk reduce el ruido al comunicarse entre el emisor y el receptor del gráfico. Por lo tanto, esta directriz es importante porque tiene raíces tanto en los principios de escritura como en los de percepción.
Ejemplo 21.3.1: Recibos de Primas de Compañías de Seguros de Vida.
La Figura 21.7(a) es una adaptación de un gráfico de la página 69 del Life Insurance Fact Book (1994). El gráfico informa 15 piezas de información: 5 años y 2 porcentajes por cada año (un tercer porcentaje se encuentra por sustracción). Una caja tridimensional representa cada porcentaje, y cada caja muestra diferentes sombreados para representar las tres líneas de negocio: salud, anualidad y vida. Estas cifras podrían reportarse de manera compacta en una tabla pequeña. Sin embargo, considerando que un gráfico puede ayudar al receptor a apreciar las tendencias en las cifras, la simplicidad del gráfico debería reflejar la simplicidad de la información disponible en las cifras. En particular, un pequeño símbolo de trazado es suficiente para informar un porcentaje. Una caja tridimensional sombreada no es necesaria. Es interesante que la caja tridimensional fue una “innovación” en 1994. Las ediciones anteriores del Fact Book usaban cajas bidimensionales. El volumen de chartjunk dio un gran salto en 1994.
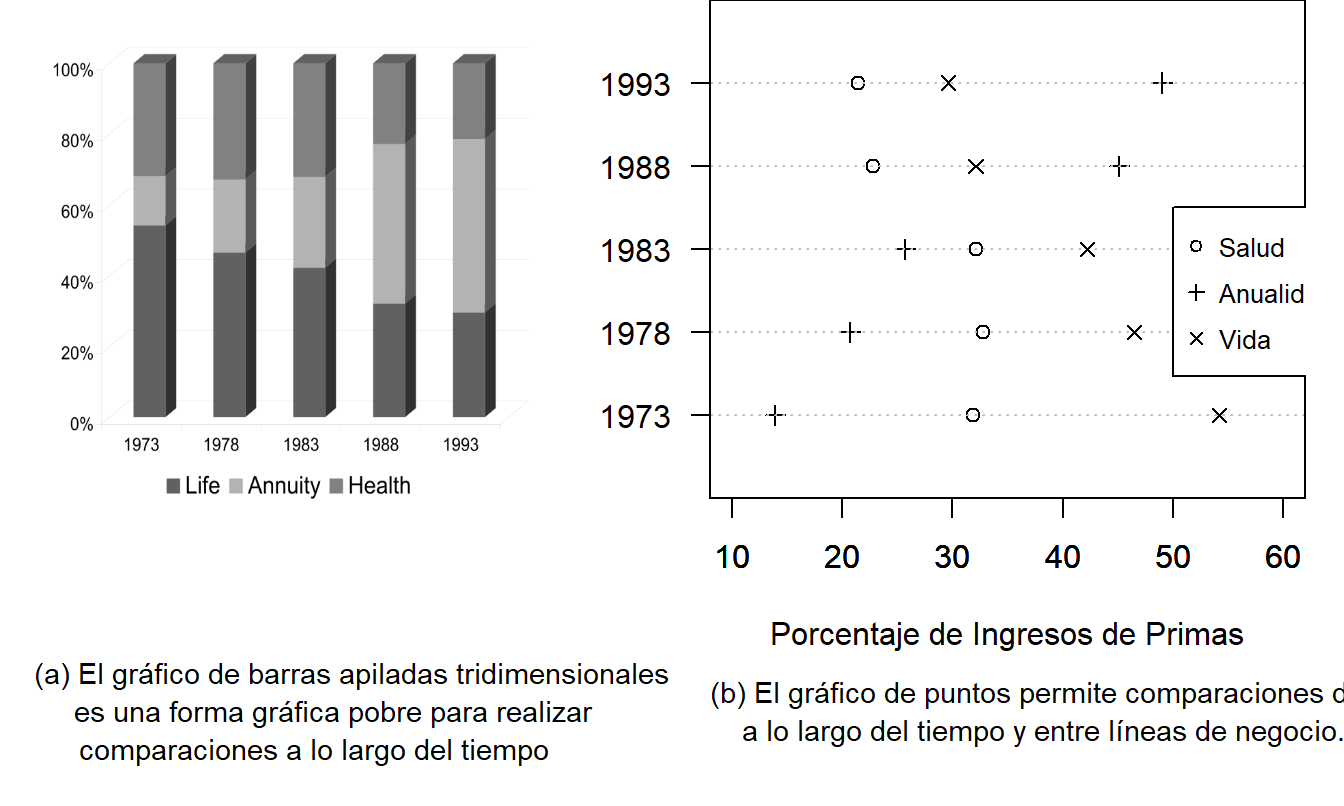
Figura 21.7: Distribución de los Recibos de Primas, 1973-1993. El exceso de chartjunk en (a) oculta el gran cambio en los tipos de distribución entre 1983 y 1988.
Código R para Generar la Figura 21.7
La Figura 21.7(b) es un gráfico de puntos, discutido por Cleveland (1994). Diferentes símbolos de trazado muestran las diferentes líneas de negocio. Las marcas en el eje horizontal inferior nos ayudan a estimar los porcentajes, y las líneas de cuadrícula punteadas nos ayudan a escanear el gráfico para identificar los símbolos de interés. Los cambios importantes, y las magnitudes aproximadas de esos cambios, que ocurrieron entre 1983 y 1988 son claros aquí.
Directriz Dos: Usar Múltiplos Pequeños para Fomentar Comparaciones y Evaluar Cambios
El pensamiento estadístico se orienta hacia la comparación de mediciones de diferentes entidades y la evaluación del cambio de una medición a lo largo del tiempo u otra unidad de medición. Las representaciones gráficas están inherentemente limitadas al retratar comparaciones o evaluar cambios porque son medios estáticos y bidimensionales. Los gráficos que contienen múltiples versiones de una forma gráfica básica, cada versión retratando una variación del tema básico, fomentan comparaciones y evaluaciones de cambio. Al repetir una forma gráfica básica, promovemos el proceso de comunicación.
Tufte (1997) afirma que usar múltiplos pequeños en representaciones gráficas logra los mismos efectos deseables que usar estructuras paralelas en la escritura. La estructura paralela en la escritura es exitosa porque permite a los lectores identificar una relación en una oración solo una vez y luego concentrarse en el significado de cada elemento individual de la oración, como una palabra, frase o cláusula. La estructura paralela ayuda a lograr economía de expresión y a vincular ideas relacionadas para comparación y contraste. De manera similar, los múltiplos pequeños en gráficos nos permiten visualizar relaciones complejas entre diferentes grupos y a lo largo del tiempo.
La sección 21.2 ilustró el uso de múltiplos pequeños. En cada figura, los dos gráficos representados eran idénticos, excepto por el cambio en la escala; este uso de estructura paralela nos permitió demostrar la importancia de la escala al interpretar gráficos. El Ejemplo 21.3.2 ilustra otra aplicación de múltiplos pequeños en gráficos, el gráfico de puntos multi-vía de Cleveland (1993).
Ejemplo 21.3.2: Importancia Relativa de las Fuentes de Riesgo. La Figura 21.8, llamada un gráfico de puntos multi-vía, demuestra conclusiones obtenidas utilizando un modelo introducido en Frees (1998) sobre la importancia relativa de las fuentes de riesgo dentro de un bloque de contratos de seguro a corto plazo. Las fuentes de riesgo son el entorno estocástico de intereses, la frecuencia de siniestros (mortalidad) y la posibilidad de un evento catastrófico (desastre). La importancia relativa de estas tres fuentes de riesgo se considera permitiendo que varíen dos parámetros de interés. Estos parámetros son el año esperado hasta el desastre y, en caso de desastre, la proporción esperada (probabilidad) de asegurados que sucumbirán al desastre.
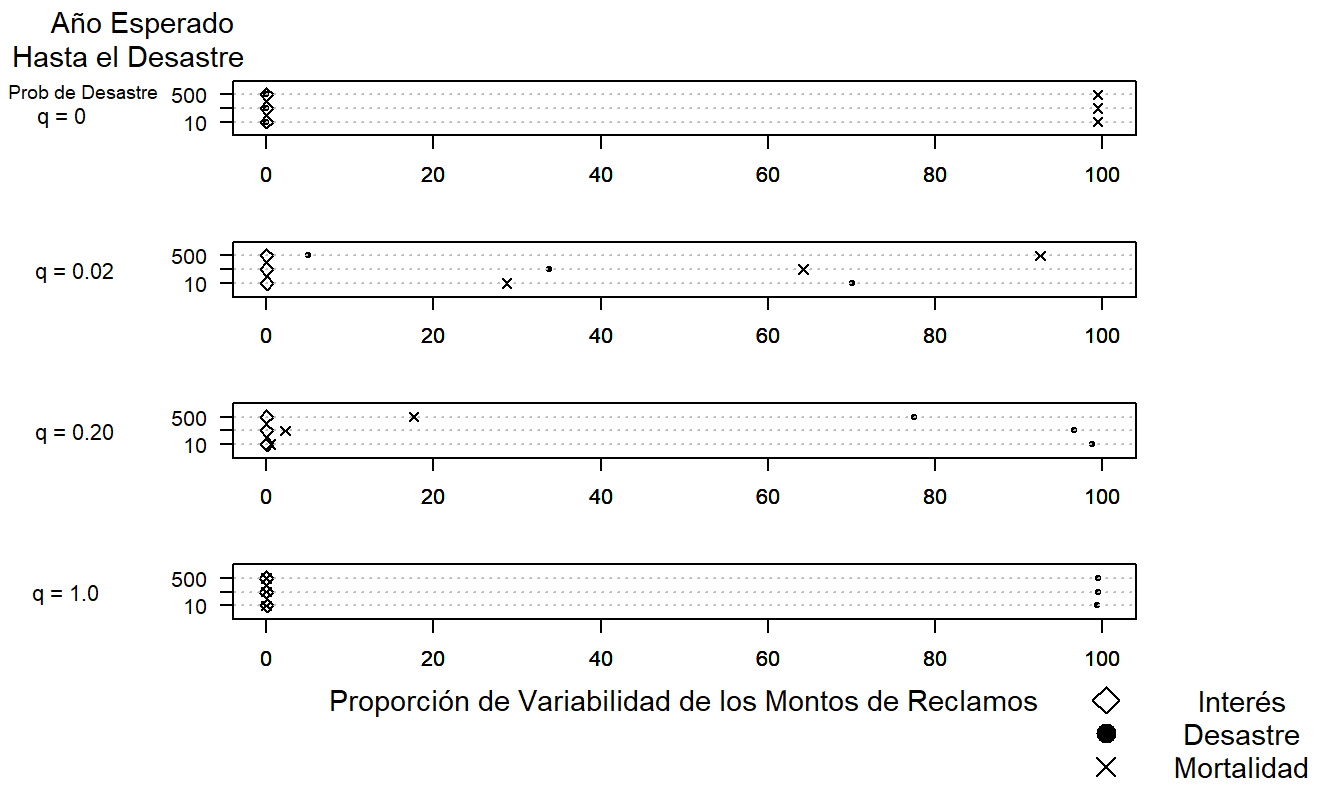
Figura 21.8: La Importancia Relativa de las Fuentes de Riesgo. Este gráfico complejo nos permite visualizar diferencias en las fuentes de riesgo (intereses, desastre y mortalidad), el año esperado hasta el desastre y la probabilidad de desastre. El gráfico de puntos multi-vía demuestra la rapidez con la que aumenta la importancia del componente de desastre a medida que aumenta la probabilidad de desastre.
Código R para Generar la Figura 21.8
La Figura 21.8 muestra que cuando ningún asegurado sucumbe a un desastre (\(q = 0\)), el componente de frecuencia, mortalidad, domina las otras fuentes de riesgo. En el extremo opuesto, cuando todos los asegurados sucumben a un desastre (\(q = 1\)), el componente de desastre domina los otros factores de riesgo. Esto es cierto incluso cuando el tiempo esperado hasta el desastre es de 500 años. Para los casos intermedios, ya sea que aumente la proporción esperada de asegurados que sucumben al desastre o que disminuya el tiempo esperado hasta el desastre, la importancia del componente de desastre aumenta a expensas del componente de mortalidad. Debido a la naturaleza a corto plazo del contrato considerado, el componente de interés no juega un papel importante en la Figura 21.8.
Esta historia sobre la importancia relativa no podría contarse utilizando expresiones analíticas debido a la complejidad de los modelos subyacentes. Sin embargo, la historia detrás de la Figura 21.8 podría contarse usando tablas. La ventaja de la Figura 21.8 es que permite al espectador realizar comparaciones sobre tres diferentes fuentes de riesgo mientras dos parámetros de interés varían. Aunque dichas comparaciones son posibles con tablas, los gráficos son dispositivos más efectivos.
Directriz Tres: Utilice Gráficos Complejos para Representar Patrones Complejos
Muchos autores creen que un gráfico debe ser simple y comprendido de inmediato por el espectador. Los gráficos simples son deseables porque pueden transmitir su mensaje a una amplia audiencia y pueden mostrarse rápidamente y ser entendidos de inmediato. Aunque esta noción puede ser apropiada para la escritura popular, en la escritura profesional el concepto de comprensión instantánea es limitante, ya que excluye la idea de que los gráficos demuestren ideas complejas. Los patrones complejos deben representarse de la manera más simple posible, aunque los patrones en sí no deben simplificarse innecesariamente.
Una forma en que un gráfico puede representar patrones complejos es permitiendo que algunos de sus elementos básicos cumplan más de un propósito. Tufte (1983) llamó a estos elementos multifuncionales. Por ejemplo, podemos usar símbolos de representación no solo para elementos correspondientes a las escalas horizontal y vertical, sino también para un nivel de una variable categórica.
Ejemplo 21.3.3: Frecuencia y Severidad de los Costos Hospitalarios. La Figura 21.9 muestra la relación entre los costos hospitalarios promedio y la frecuencia de uso hospitalario. Estos datos corresponden al año 1989 y fueron obtenidos de la Oficina de Información de Atención Médica del Departamento de Servicios de Salud y Bienestar de Wisconsin, y se analizan más a fondo en la Sección 4.4. Los datos representan promedios en el estado de Wisconsin, desglosados por nueve áreas de servicio de salud, tres tipos de proveedores (pago por servicio, organización de mantenimiento de la salud y otros) y tres tipos de grupos relacionados con diagnósticos (GRDs). Los tres GRDs, números 209, 391 y 430, representan reparación mayor de articulaciones y miembros, recién nacidos normales y psicosis, respectivamente. Cada símbolo de representación en la Figura 21.9 representa una combinación de área de servicio de salud, tipo de pagador y tipo de GRD. El eje horizontal proporciona el número de pacientes admitidos en 1989 para cada combinación, en unidades logarítmicas naturales. La escala vertical muestra el costo promedio hospitalario por alta para cada combinación, también en unidades logarítmicas naturales.
La historia en el panel izquierdo, Figura 21.9(a), es una de economías de escala crecientes. Es decir, las combinaciones de áreas de servicio de salud, tipo de pagador y GRD que tienen un mayor número de pacientes, medido por altas, tienen costos más bajos. En la Figura 21.9(a) se observa una relación negativa sustancial; el coeficiente de correlación es -0.43. Esto es cierto a pesar del punto aberrante en la región inferior izquierda de la Figura 21.9(a). El punto aberrante es menos importante económicamente que los demás, ya que representa una combinación con solo dos altas. Cuando se elimina este punto, la correlación pasa a ser -0.50, representando así una relación negativa aún más fuerte.

Figura 21.9: Costo Logarítmico por Alta versus Número Logarítmico de Altas. Al agregar un código de símbolo de trazado para el nivel de GRD, se evidencian tres grupos distintos. Los tres GRDs, 209, 391 y 430, representan reparación mayor de articulaciones y extremidades, recién nacidos normales y psicosis, respectivamente.
Código R para Generar la Figura 21.9
A pesar de su simplicidad, la Figura 21.9(a) oculta una relación importante. El panel derecho, Figura 21.9(b), es una reinterpretación de la Figura 21.9(a) que incluye diferentes símbolos para diferentes GRDs. Aquí, la historia es opuesta a la de las economías de escala crecientes. Para combinaciones que representan reparaciones mayores de articulaciones y extremidades y recién nacidos normales, la relación entre frecuencia y costo es bastante plana. Para estos GRDs hay pocas economías de escala. Para el GRD de psicosis, número 430, la Figura 21.9(b) muestra una pequeña relación positiva entre frecuencia y costo, incluso descontando la combinación con solo dos pacientes dados de alta.
Los dos paneles ilustran un fenómeno en estadística conocido como la paradoja de Simpson, o un problema de agregación de datos. Consulte la Sección 4.4 para más discusión. El punto importante para este capítulo es que, a veces, los gráficos simples son engañosos. Los gráficos complejos pueden requerir más tiempo para que los espectadores los interpreten, pero resumen de manera más efectiva las relaciones complejas.
Directriz Cuatro: Relacione el Tamaño del Gráfico con el Contenido Informativo
“La pregunta de qué tan grande debe ser el gráfico” es importante. Los límites de tamaño son claros. Los gráficos no deben ser tan pequeños que no sean claramente legibles, especialmente después de reproducciones que degraden la imagen, ni deben ser tan grandes que excedan una página. Los gráficos grandes dificultan la comparación de elementos dentro del gráfico, lo que frustra un propósito principal de los gráficos.
Dentro de estos límites, un gráfico debe ser proporcional a la cantidad de información que contiene. Para discutir la proporción de contenido informativo, Tufte (1983) introdujo la densidad de datos de un gráfico. Esto se define como el número de entradas de datos por unidad de área del gráfico. Para comparar el tamaño del gráfico y la información, la densidad de datos es una cantidad que se debe maximizar, ya sea aumentando el número de entradas de datos o reduciendo el tamaño del gráfico. Al examinar esta densidad en varias publicaciones populares, Tufte concluyó que la mayoría de los gráficos podrían reducirse de manera efectiva.
Por ejemplo, la Figura 21.7(a) es un gráfico con una baja densidad de datos. Este gráfico representa solo 15 números. Con un área de aproximadamente 9 pulgadas cuadradas, la densidad de datos de este gráfico es aproximadamente 15/9. En comparación, la Figura 21.10 muestra aproximadamente 600 números. Aunque el área de la Figura 21.10 es aproximadamente el doble que la de la Figura 21.7(a), la densidad de datos es mucho mayor en la Figura 21.10 que en la Figura 21.7(a).
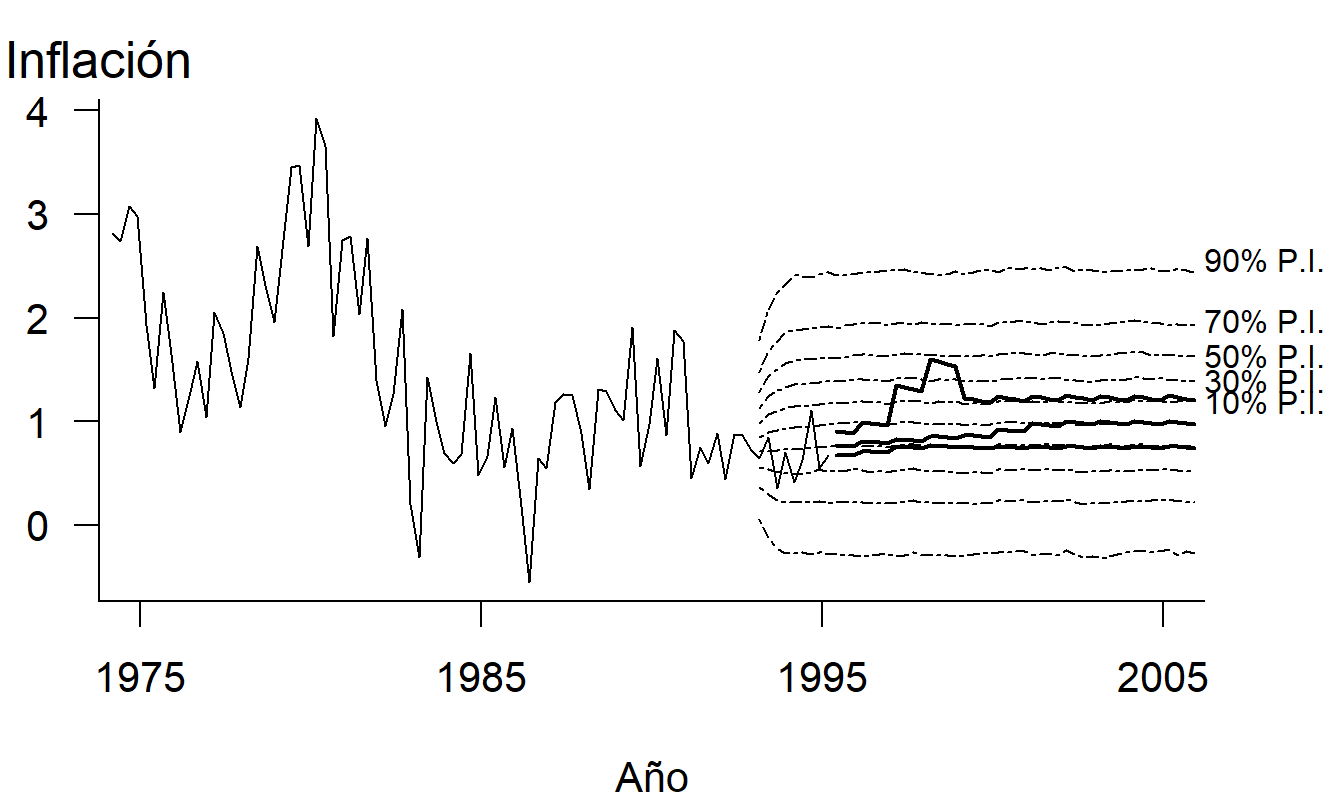
Figura 21.10: Comparación de Intervalos de Predicción Estocásticos con Experiencia Real y Suposiciones de la Seguridad Social. Las líneas sólidas delgadas representan las tasas de inflación reales, y las líneas sólidas gruesas representan las proyecciones de expertos de la Seguridad Social. Las líneas punteadas representan intervalos de predicción generados por un modelo de series temporales estocástico. Este gráfico complejo permite a los espectadores realizar comparaciones basadas en aproximadamente 600 puntos.
Código R para Generar la Figura 21.10
Ejemplo 21.3.4: Pronósticos de la Tasa de Inflación.
La Figura 21.10 es un gráfico complejo que contiene mucha información sobre un tema complejo, la previsión de la tasa de inflación (CPI) para las proyecciones de los fondos de la Seguridad Social (Frees et al. 1997). El gráfico muestra la experiencia real de las tasas trimestrales de inflación hasta el primer trimestre de 1995. La experiencia hasta 1992 se utilizó para ajustar un modelo de series temporales descrito en Frees et al. (1997), y este modelo se utilizó para generar intervalos de predicción (PIs) de la tasa de inflación. Estos intervalos de predicción pueden compararse con datos retenidos que no se usaron para ajustar el modelo (1993-1995), así como con las proyecciones de inflación de los expertos en Seguridad Social. Las líneas gruesas representan las proyecciones de inflación de alto, intermedio y bajo costo determinadas por los expertos en Seguridad Social.
La Figura 21.10 es compleja y puede no ser comprendida de inmediato por el espectador. Sin embargo, casi cada trazo dentro de la región de datos representa información numérica. Aunque es compleja, la Figura 21.10 permite al espectador comparar (1) 20 años de experiencia con un pronóstico de 10 años, (2) datos recientes retenidos con los pronósticos y (3) proyecciones de expertos con pronósticos generados por un modelo de series temporales. La complejidad del gráfico refleja la complejidad de pronosticar tasas de inflación; esta complejidad no se debe a elementos innecesarios que distraen a los espectadores y los hacen más “interesados” en el gráfico.
Directriz Cinco: Utilizar Formas Gráficas que Promuevan Comparaciones
Los creadores de gráficos a menudo enfrentan la elección de varias formas gráficas que podrían usarse para representar una característica de los datos. Como describimos en la Directriz Ocho, el conocimiento del receptor sobre formas gráficas puede influir en la elección. La percepción gráfica también es un determinante importante. En la Sección 21.4, discutimos este tema en detalle. Lo incluimos aquí como parte de la Sección de Directrices para completar.
Directriz Seis: Integrar Gráficos y Texto
Los gráficos de datos deben integrarse cuidadosamente con texto, tablas y otros gráficos. Una leyenda resume el gráfico y su mensaje principal, pero el texto circundante desarrolla el tema que lleva al mensaje y discute su impacto. Aunque “una imagen vale más que mil palabras,” un gráfico necesita texto de apoyo. Tufte (1983) alienta a los lectores y escritores a pensar en los gráficos de datos como párrafos y a tratarlos como tales.
Los gráficos de datos pueden complementarse con una presentación tabular de datos: los gráficos pueden resaltar relaciones entre los datos, y las tablas pueden presentar descripciones numéricas precisas de los datos. Los dos modos son complementarios. Un buen dispositivo de escritura es colocar una presentación gráfica en el cuerpo principal del informe y reforzar el gráfico con una presentación tabular en un apéndice.
La Asociación Estadounidense de Estadística, en su Guía de Estilo para publicaciones en revistas, nos recuerda que una leyenda detallada es útil para interpretar gráficos. La Guía de Estilo recomienda que una leyenda describa un gráfico, llame la atención sobre las características importantes del gráfico y explique su importancia.
Directriz Siete: Demostrar un Mensaje Importante
Las leyendas detalladas y los gráficos deben reforzar mensajes que se desarrollan en el cuerpo principal del texto. Para ilustrar, al considerar formas de representar un conjunto de datos complejo, elija una forma gráfica que destaque un mensaje importante. Con demasiada frecuencia, los creadores de gráficos muestran características de los datos que no forman parte del tema que se está desarrollando.
Cleveland (1994) recomienda que “pongamos las conclusiones principales en una forma gráfica.” En el análisis de datos de regresión, las conclusiones principales se refieren a patrones en los datos que se resumen utilizando modelos. Generalmente, las conclusiones principales se presentan mejor de forma gráfica. Los gráficos muestran una gran cantidad de información que es retenida por el espectador porque se visualiza. Los gráficos comunican patrones directamente al espectador, sin usar una ecuación para representar los patrones. De esta manera, se puede llegar a una audiencia más amplia que si la presentación dependiera únicamente de una interpretación basada en modelos de los datos. Además, los patrones sugeridos por un gráfico refuerzan aquellos representados por un modelo, y viceversa. Así, las dos herramientas, gráficos y modelos, se refuerzan y fortalecen mutuamente.
Tukey (1977) afirma que “el mayor valor de una imagen es cuando nos obliga a notar lo que nunca esperábamos ver.” Los fenómenos inesperados suelen ser eventos memorables; los espectadores de gráficos recuerdan estos resultados, lo que los hace poderosos. Al escribir este capítulo, no esperábamos los resultados de la Figura 21.6. Esta figura demuestra que el desempleo aumenta mucho más rápido de lo que disminuye; es un poderoso ejemplo del uso de relaciones de aspecto.
Directriz Ocho: Conozca a su Audiencia
Un precepto básico de la escritura efectiva, la familiaridad con la audiencia, también es válido para diseñar gráficos efectivos. Como se indicó en la Introducción, nuestra principal motivación al desarrollar directrices es fomentar la comunicación precisa y concisa de ideas cuantitativas a una audiencia científica utilizando un medio escrito. Como se discute en la Sección 21.4, la forma gráfica está subordinada al papel real de la presentación gráfica, comunicar ideas cuantitativas del creador al espectador de un gráfico. Si la audiencia no comprende la forma gráfica, entonces esta forma dificultará el flujo de comunicación en lugar de facilitarlo. Por lo tanto, cada una de las siete directrices ya discutidas puede modificarse o incluso ignorarse en ocasiones, dependiendo de la audiencia del gráfico.
Para ilustrar, en el Ejemplo 21.3.1 argumentamos que el gráfico de puntos era superior al gráfico de barras apiladas tridimensional. Como otro ejemplo, en la Sección 21.4 argumentamos que los gráficos de pastel son comunicadores ineficaces de información según la ciencia de la percepción cognitiva. Sin embargo, para algunas audiencias, los creadores de gráficos preferirán las formas menos efectivas según el nivel de familiaridad de la audiencia. Esperamos que la práctica eventualmente cambie de estos modos de comunicación ineficaces. Aun así, es importante reconocer los antecedentes de la audiencia del gráfico. Recomendamos que los creadores de gráficos no naden tanto contra la corriente del mal diseño gráfico como que ajusten su curso hacia modos de comunicación más efectivos.
21.4 Fundamentos Empíricos para las Directrices
Esta sección consiste en dos aspectos científicos diferentes de los estudios gráficos: la ciencia de la percepción y encuestas sobre la práctica gráfica.
Este capítulo no incluye varias formas gráficas que son comunes en publicaciones empresariales y en la prensa popular, como gráficos de pastel, pictogramas y gráficos de barras apiladas. De hecho, hemos mostrado gráficos de barras apiladas en la Sección 21.3 solo como un ejemplo de cómo no dibujar figuras. ¿Por qué estas formas gráficas ampliamente utilizadas no son adoptadas en un capítulo que enfatiza los gráficos de datos? Las razones radican en cómo las formas gráficas comunican información y cómo percibimos la información gráfica. Demostramos que, dada nuestra percepción de la información, los gráficos de pastel y las barras apiladas son comunicadores deficientes de información numérica.
Como se describe en la Sección 21.1, los gráficos de datos codifican información, y nosotros, como espectadores, desciframos esta información al visualizar un gráfico. La eficiencia de esta transmisión puede considerarse en el contexto de la psicología cognitiva, la ciencia de la percepción. Esta disciplina proporciona un marco para distinguir entre diferentes tipos de procesamiento de información que hacemos al descifrar gráficos. Identificar diferentes tipos de procesamiento de información nos ayudará a decidir qué formas gráficas son efectivas y cuáles no lo son.
Tabla 21.1 es una lista ordenada de tareas básicas de percepción gráfica, según Cleveland (1994). Aquí, el orden comienza con un conjunto de tareas que es menos difícil para un espectador realizar y termina con un conjunto que es más difícil. Así, por ejemplo, juzgar la posición a lo largo de una escala común es lo menos difícil para los espectadores, y juzgar las sombras relativas de colores y densidad (la cantidad de tinta) es lo más difícil.
Table 21.1. Tareas Básicas de Percepción Gráfica
\[ \small{ \begin{array}{l}\hline \text{1. Posición a lo largo de una escala común} \\ \text{2. Posición a lo largo de escalas idénticas no alineadas} \\ \text{3. Longitud} \\ \text{4. Ángulos y pendientes} \\ \text{5. Área} \\ \text{6. Volumen} \\ \text{7. Color y densidad} \\ \hline \end{array} } \]
Para comprender la dificultad relativa de las tareas, Cleveland y McGill (1984) realizaron una serie de pruebas en muchos sujetos experimentales. Para ilustrar, las Figuras 12.11(a)-(e) presentan una serie de pruebas que son análogas a las primeras cinco tareas. Cleveland y McGill resumieron el desempeño de los sujetos experimentales calculando la precisión con la que realizaron cada conjunto de tareas. A través de estas medidas de precisión relativa y argumentos de la psicología cognitiva, Cleveland y McGill desarrollaron el orden presentado en Tabla 21.1.
Figura 21.11(a). Experimento para Juzgar la Posición a lo Largo de una Escala Común. Evaluar los valores relativos de A, B, C y D a lo largo de esta escala de 100 puntos.
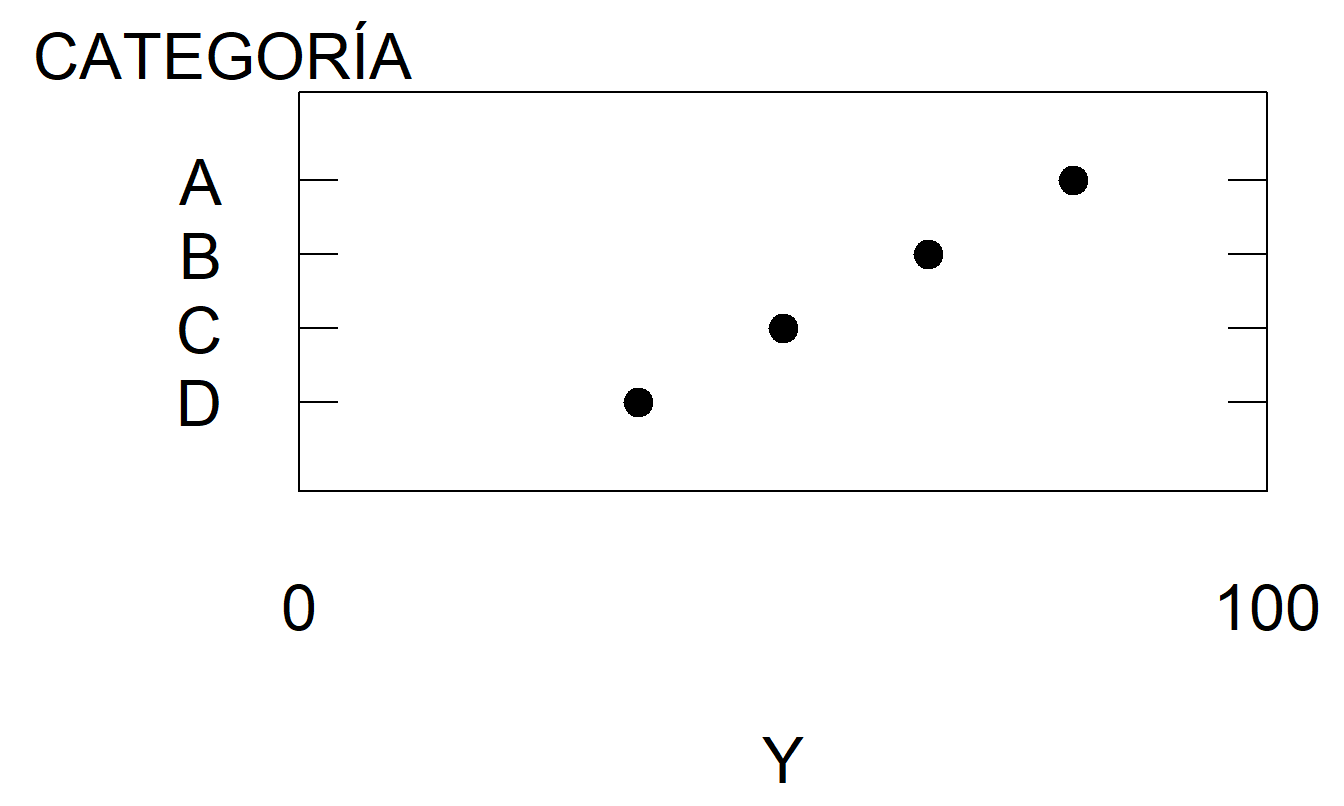
Figura 21.11(b). Experimento para Juzgar la Posición en Escalas Idénticas no Alineadas. Evalúe los valores relativos de A, B, C y D en una escala común de 100 puntos.
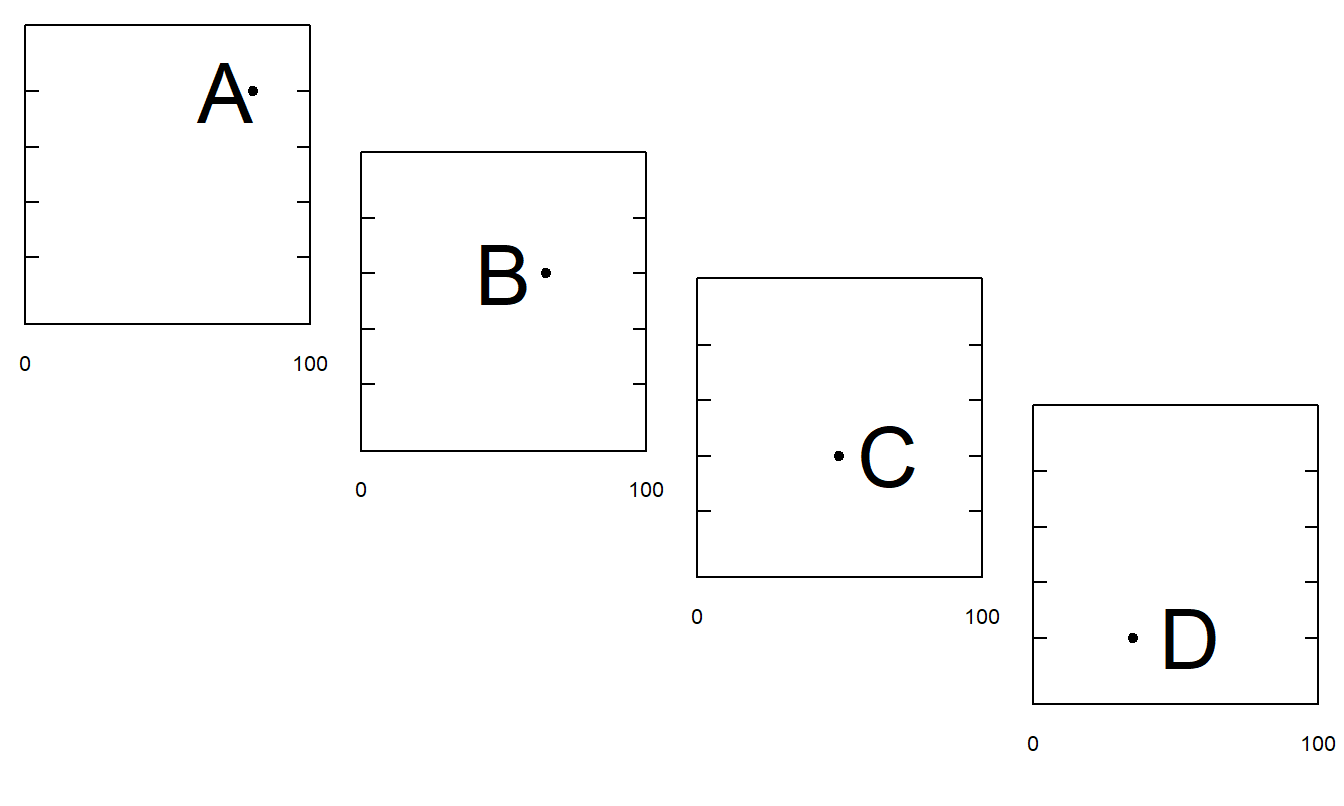
Figura 21.11(c). Experimento para Entender Juicios de Longitud. Suponga que la línea A tiene 100 unidades de longitud. Evalúe las longitudes relativas de las líneas B, C y D.
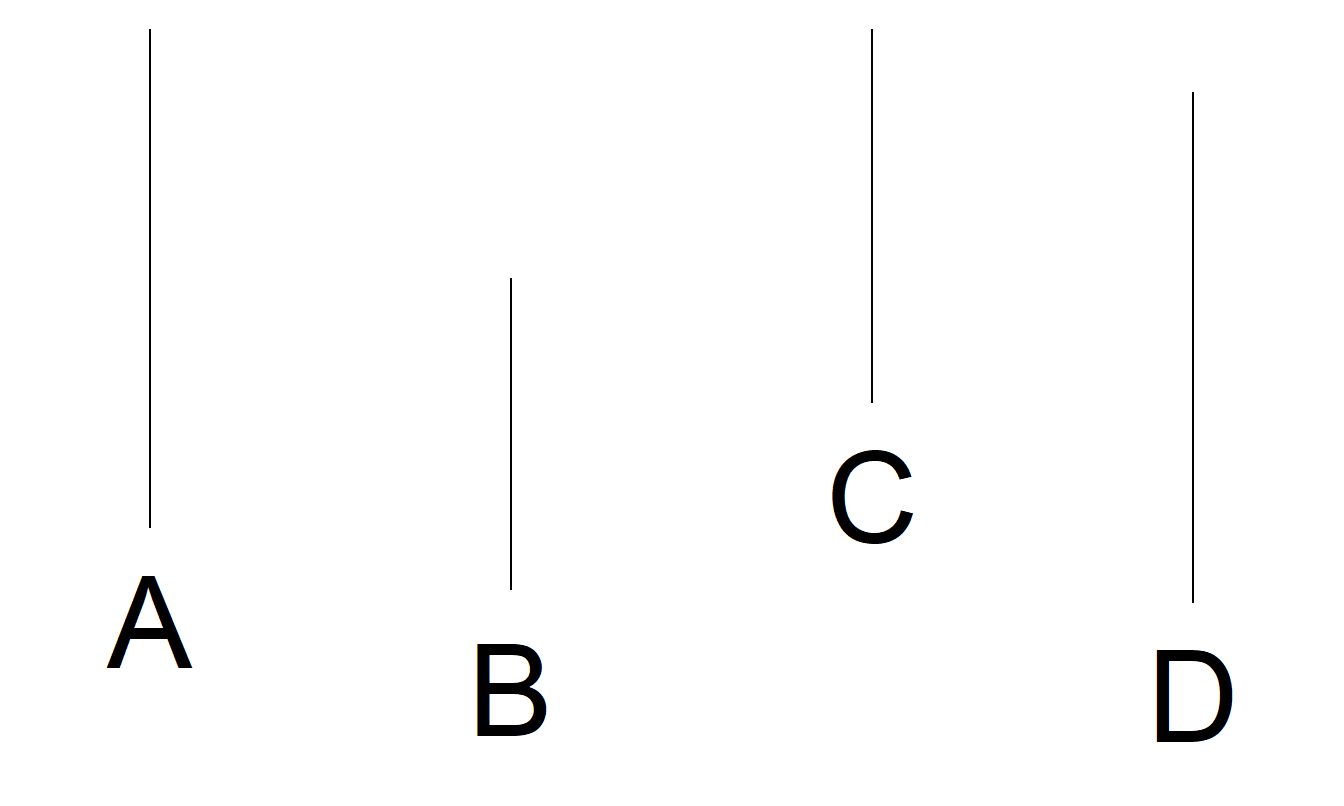
Figura 21.11(d). Experimento para Entender Juicios de Ángulos. Suponga que el ángulo A tiene 100 unidades. Evalúe los valores relativos de los ángulos B, C y D.
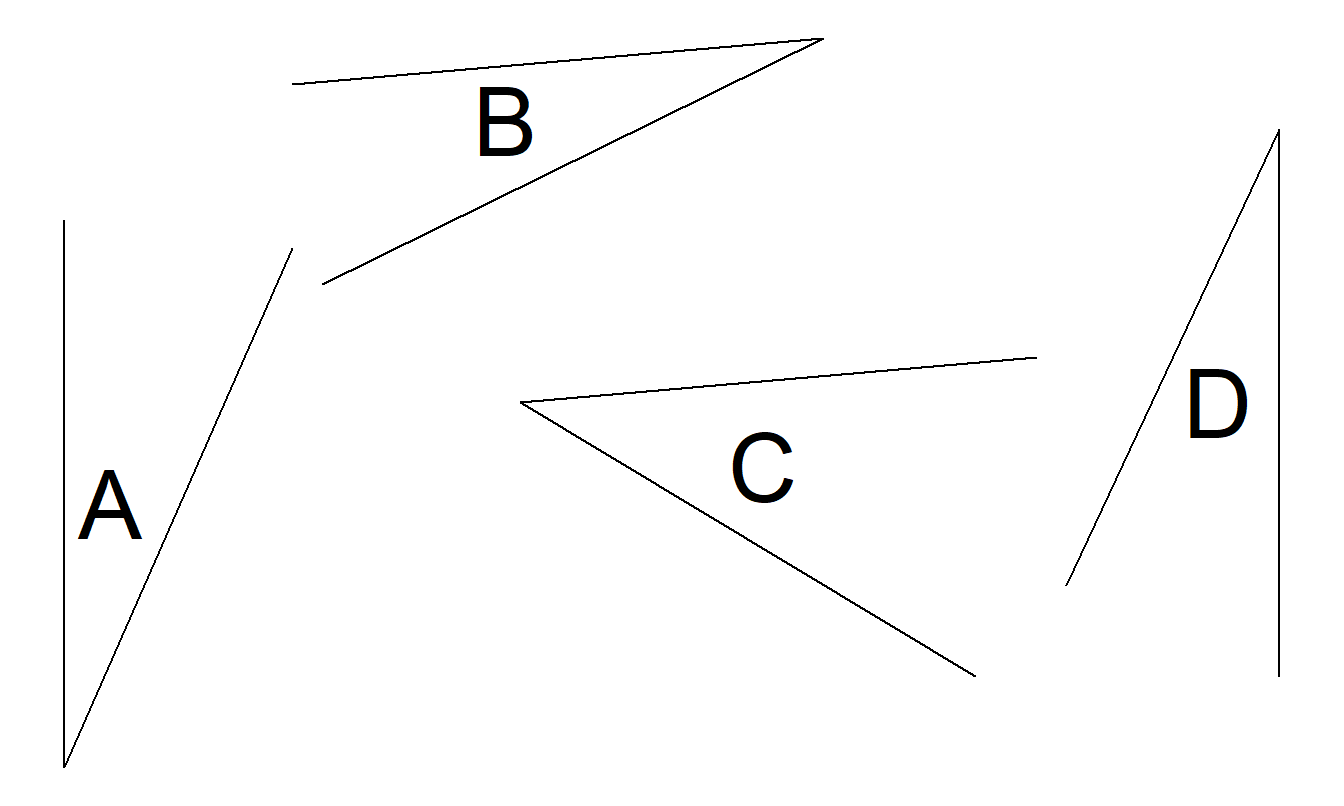
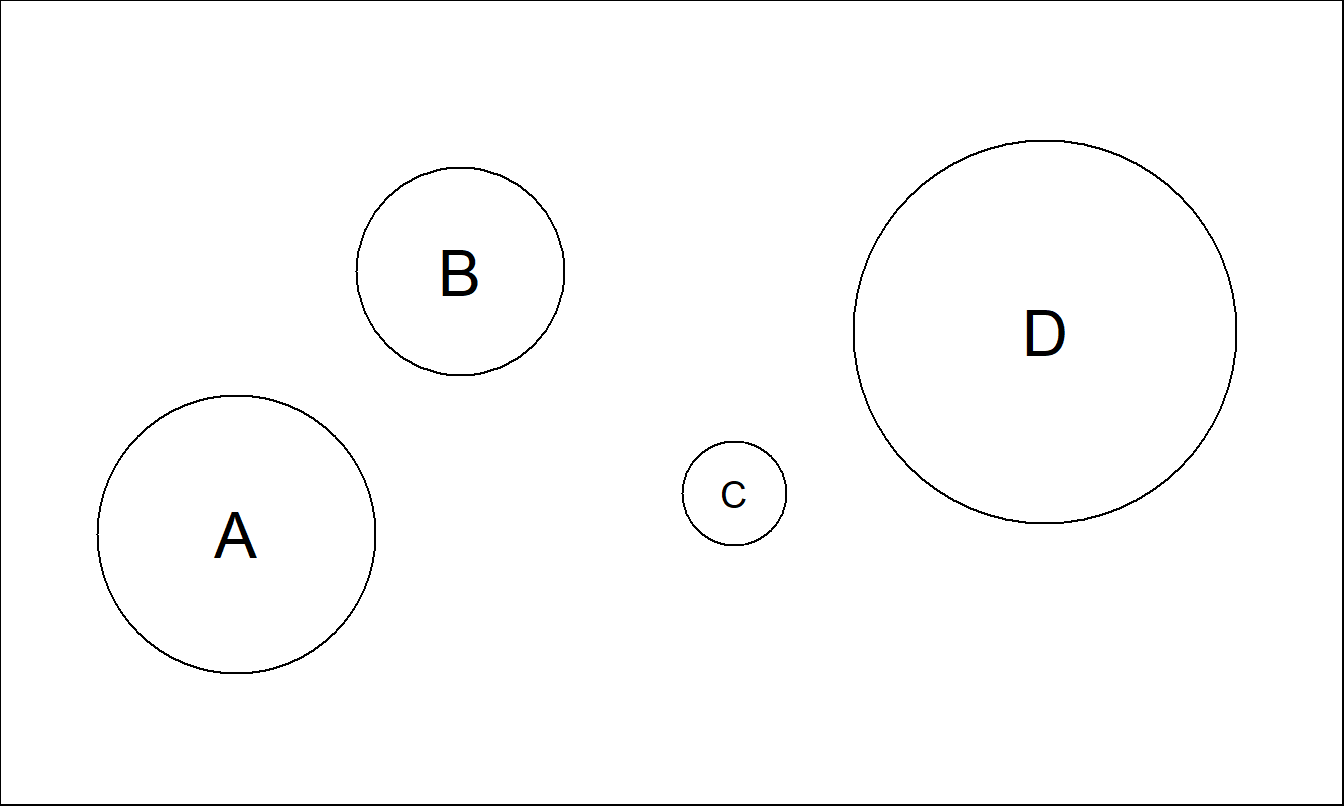
Figura 21.11(e). Experimento para Entender Juicios de Áreas. Suponga que el círculo A tiene un área de 100 unidades. Evalúe las áreas relativas de los círculos B, C y D.
Este capítulo no discute el uso de colores debido a las complejidades para codificarlos y decodificarlos de manera efectiva. Remitimos a los lectores interesados a Cleveland (1994, Sección 3.13) y Tufte (1990, Capítulo 5) para obtener más información.
La lista ordenada de tareas de percepción gráfica puede ayudar al creador a elegir la forma gráfica adecuada para representar un conjunto de datos. Cuando se enfrenta a la elección entre dos formas gráficas, un creador debe seleccionar la que sea menos difícil para el espectador. En igualdad de condiciones, una tarea que el espectador puede realizar con menor dificultad significa que la información puede transmitirse de manera más confiable. Para ilustrar esto, discutimos dos ejemplos en los que Tabla 21.1 puede ayudar a decidir la forma gráfica adecuada para representar un conjunto de datos.
Ejemplo 21.4.1: Distribución de los Ingresos por Primas. El primer ejemplo demuestra algunas limitaciones del gráfico de barras apiladas. Para esta discusión, volvemos al Ejemplo 21.3.1. La Figura 21.7(a) es un gráfico de barras apiladas tridimensional. Ya hemos discutido la cantidad considerable de elementos innecesarios en esta figura. Incluso sin la dimensión pseudo tridimensional, el gráfico de barras apiladas requiere que el espectador haga juicios de longitud para entender, por ejemplo, la distribución de los ingresos por anualidades a lo largo del tiempo. En contraste, el gráfico de puntos en la Figura 21.7(b) requiere que el espectador haga comparaciones solo en función de posiciones a lo largo de una escala común. Como se describe en la Tabla 21.1, esta última es una tarea más fácil, lo que resulta en información más confiable para el espectador. Por lo tanto, concluimos que el gráfico de puntos es preferible al gráfico de barras apiladas.
Ejemplo 21.4.2: Distribución de Hipotecas. Nuestro segundo ejemplo demuestra la insuficiencia de los gráficos de pastel. La Figura 21.12 es una adaptación de la figura en la página 100 del Life Insurance Fact Book (1994). Representa, para los años 1973, 1983 y 1993, hipotecas comerciales, de 1 a 4 familias y agrícolas como porcentajes del total de hipotecas. Los gráficos de pastel dificultan las comparaciones. Por ejemplo, el gráfico dificulta detectar si las hipotecas agrícolas son más prevalentes que las hipotecas de 1 a 4 familias en 1983, o si los porcentajes de hipotecas agrícolas aumentaron o disminuyeron de 1973 a 1983. La comparación de porcentajes a lo largo de los años es una operación lineal, pero los gráficos de pastel requieren que decodifiquemos ángulos, una tarea difícil según el orden presentado en la Tabla 21.1. Como en el Ejemplo 21.3.1, los gráficos en la Figura 21.12 empeoran las cosas al presentarse en tres dimensiones; estas figuras no solo requieren que decodifiquemos volúmenes, sino que también aumentan considerablemente los elementos innecesarios en el gráfico. Solo nueve números se reportan en este gráfico, tres años y dos porcentajes en cada año. (El tercer porcentaje puede calcularse por sustracción).
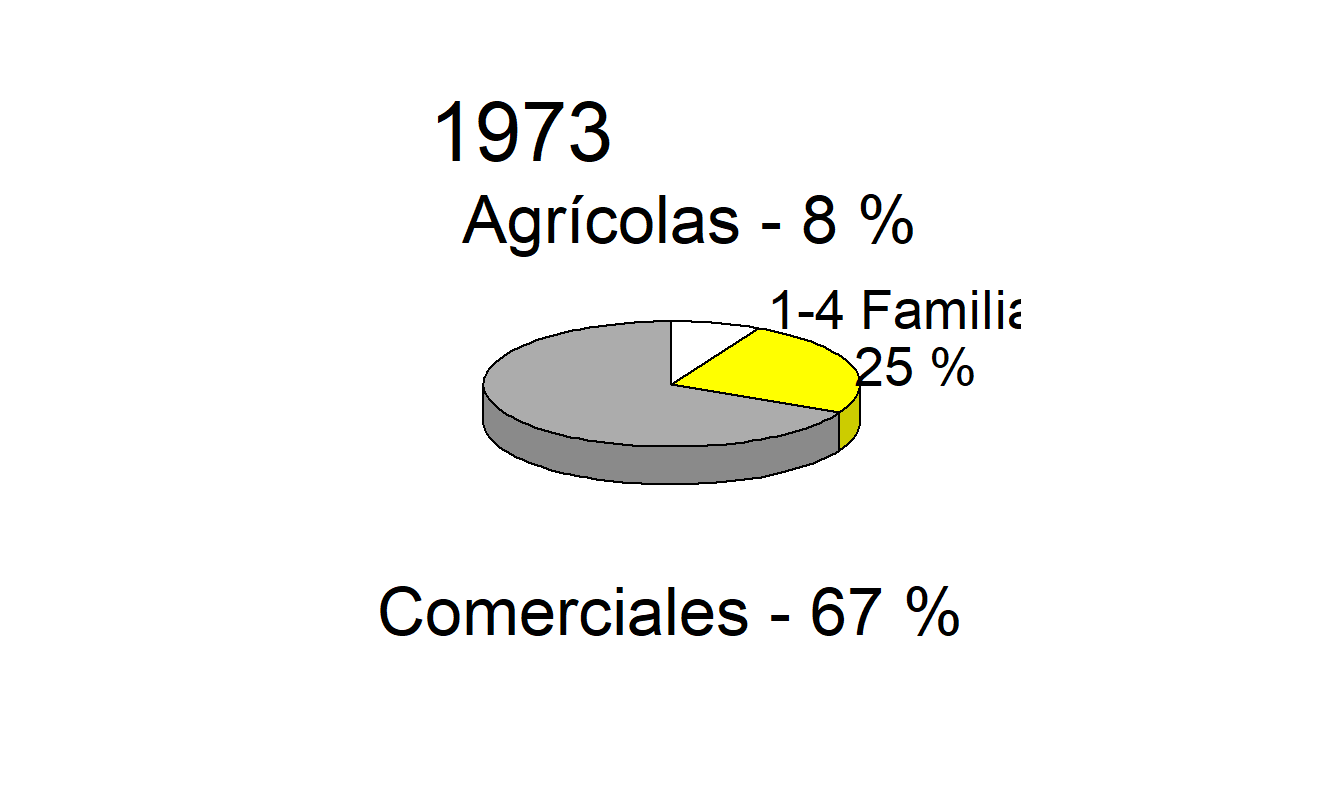
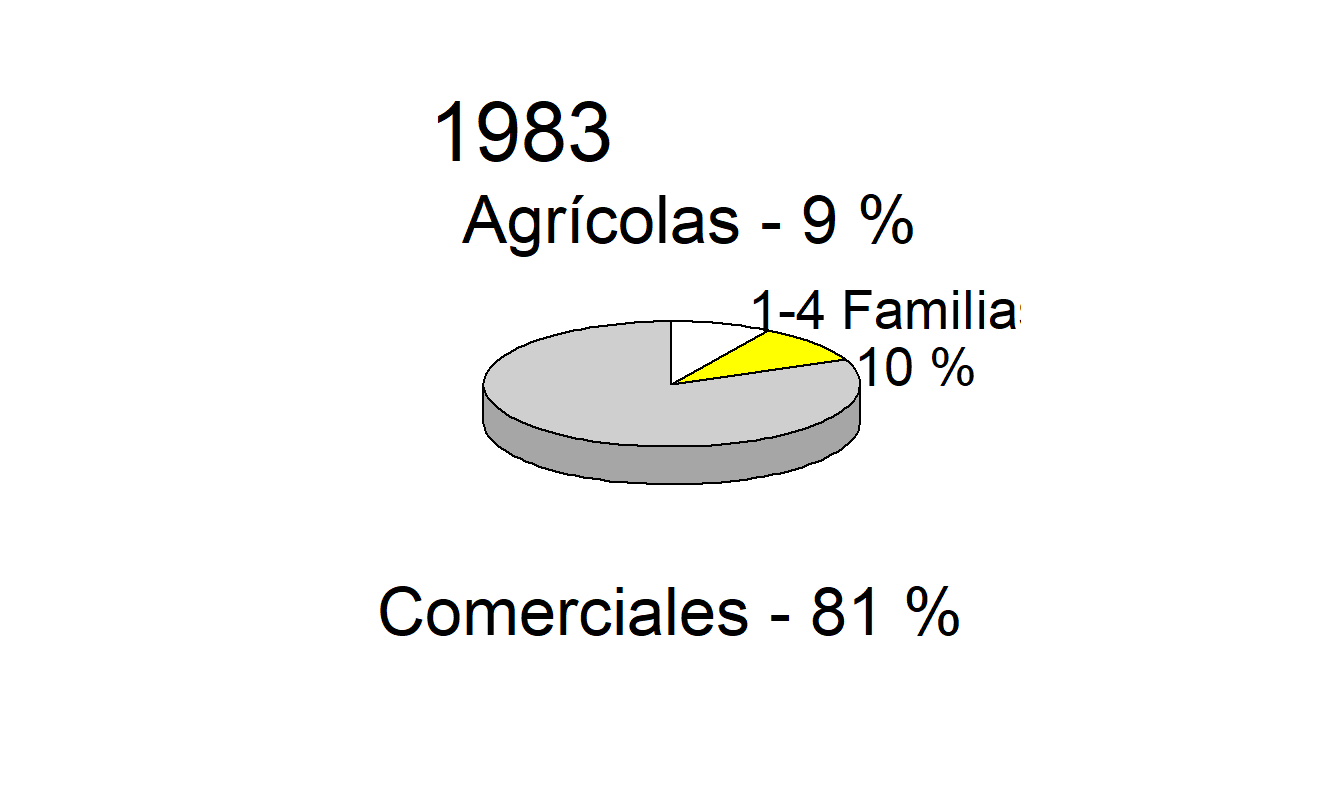
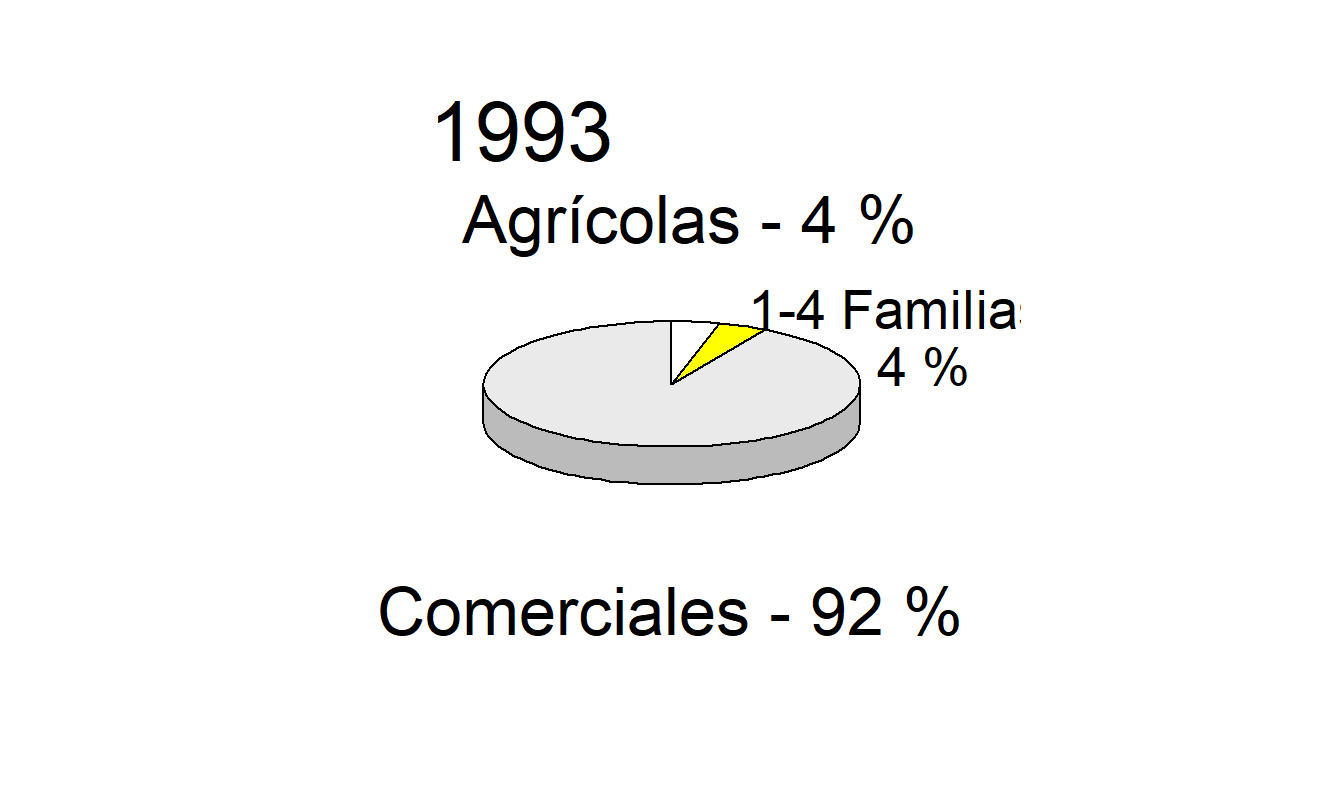
Figura 21.12: Distribución de Hipotecas para los Años 1973, 1983 y 1993. El gráfico de pastel tridimensional es una forma gráfica deficiente para hacer comparaciones a lo largo del tiempo y entre tipos de hipotecas.
Código R para Generar la Figura 21.12
Si se necesita un gráfico, entonces el gráfico de puntos en la Figura 21.13 es más que suficiente. Aquí, las comparaciones se realizan según posiciones a lo largo de una escala común, una tarea más sencilla que comparar ángulos. Los gráficos de pastel requieren que hagamos comparaciones utilizando ángulos, que son más difíciles y menos confiables que las comparaciones usando otras formas gráficas.
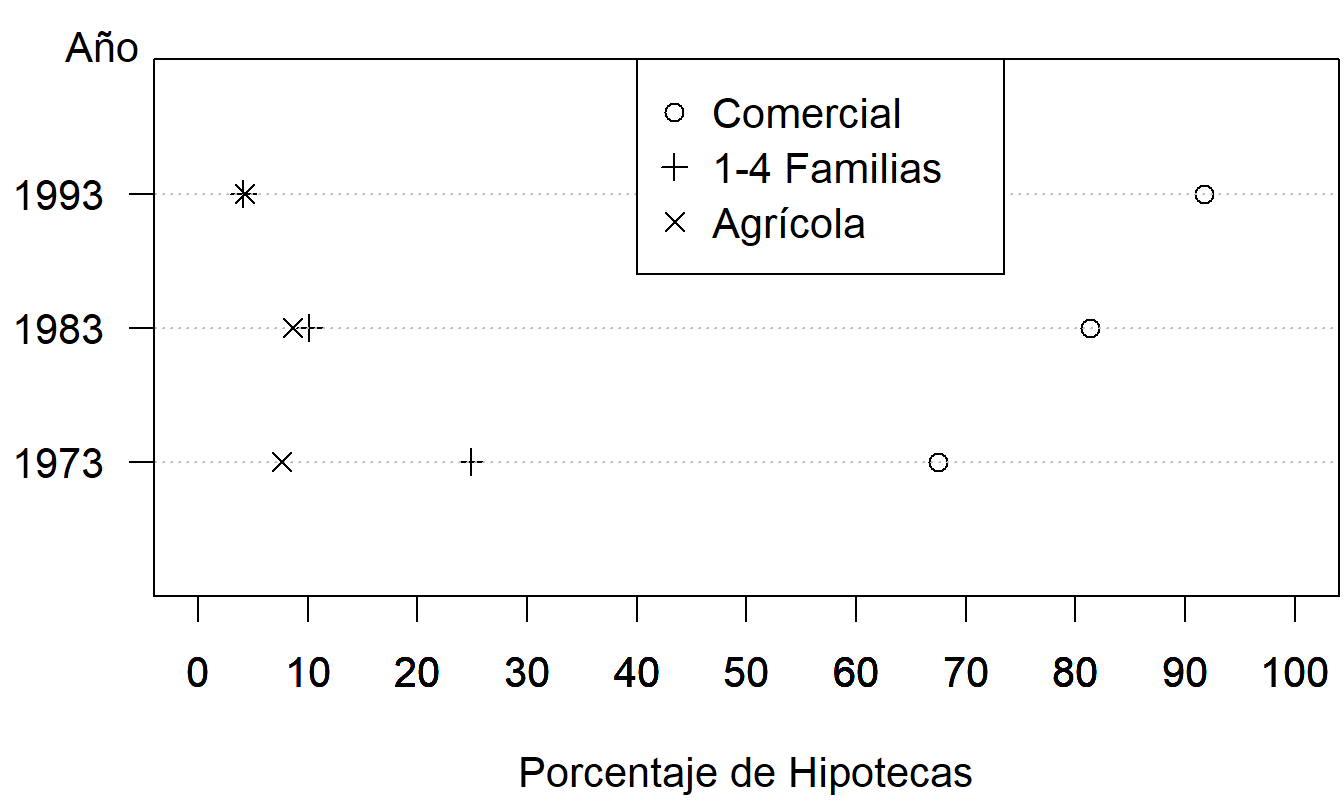
Figura 21.13: Hipotecas Comerciales, de 1-4 Familias y Agrícolas como Porcentajes del Total de Hipotecas para 1973, 1983 y 1993. Un aspecto negativo de este gráfico es la superposición de los símbolos de trazado para las hipotecas de 1-4 familias y las agrícolas en 1983 y 1993.
Código R para Generar la Figura 21.13
Tabla A.2. Hipotecas Comerciales, de 1-4 Familias y Agrícolas como Porcentajes del Total de Hipotecas para 1973, 1983, 1993
\[ \small{ \begin{array}{l|rrr} \hline & \text{Año}\\ \hline \text{Tipo de Hipoteca} & 1973 & 1983 & 1993 \\ \hline \text{Comercial} & 67.5 & 81.3 & 91.7 \\ \text{1-4 Familias} & 24.9 & 10.1 & 4.1 \\ \text{Agrícola} & 7.6 & 8.6 & 4.2 \\ \hline \end{array} } \]
Aunque la Figura 21.13 es un gráfico más efectivo que la Figura 21.12, para estos datos recomendamos una presentación tabular (Tabla A.2), que permite comparaciones claras entre tipos de hipotecas y años. Además, la Tabla A.2 ofrece información más detallada sobre los porcentajes de hipotecas que las Figuras 21.12 o 21.13. Por supuesto, siempre podemos superponer los porcentajes reales, como se hace a menudo con gráficos de pastel y como se ilustra en la Figura 21.12. Nuestra respuesta a este enfoque es cuestionar la utilidad del gráfico completo. Como en la escritura, ¡cada trazo debería aportar nueva información; que los creadores de gráficos hagan que cada trazo cuente!
21.4.1 Gráficos como Unidades de Estudio
Los estudios de prácticas gráficas en publicaciones profesionales proporcionan una base de datos importante para evaluar la prevalencia de buenas y malas prácticas, así como los cambios en estas prácticas a lo largo del tiempo. Tufte (1983, pp. 82-86) discute una encuesta de aproximadamente 4,000 gráficos seleccionados al azar de 15 publicaciones de noticias entre los años 1974 y 1980. Los gráficos se evaluaron en términos de “sofisticación”, definida como la presentación de relaciones entre variables, excluyendo series de tiempo o mapas. Cleveland y McGill (1985) reportan una encuesta similar en publicaciones científicas, evaluando la prevalencia de errores gráficos.
Harbert (1995) evaluó cada gráfico y tabla en las ediciones de 1993 de cuatro revistas de psicología utilizando 34 medidas de calidad. Las medidas de calidad se obtuvieron de la literatura de investigación actual sobre calidad gráfica. Estas medidas se convirtieron en una hoja de verificación, y una hoja de verificación fue completada para cada gráfico y tabla en las revistas de psicología seleccionadas. El estudio de Harbert generó datos sobre 439 gráficos y tablas. Resumimos el análisis de los 212 gráficos.
Harbert asignó calificaciones a los gráficos: A, AB, B, BC, C, CD, D, DF y F. Estas calificaciones reflejaron su evaluación general de los gráficos como comunicadores de información estadística. Las calificaciones fueron convertidas a valores numéricos: 4.0, 3.5, 3.0, 2.5, 2.0, 1.5, 1.0, 0.5 y 0.0. Los valores numéricos fueron la variable dependiente en una regresión. Las variables independientes fueron las 34 medidas de calidad, codificadas de manera adecuada. El propósito del estudio fue determinar qué factores eran predictores estadísticamente significativos de las calificaciones asignadas por un evaluador “experto” de gráficos. Por ensayo y error, Harbert seleccionó una ecuación de regresión lineal múltiple en la que todos los predictores eran estadísticamente significativos (nivel del 5%) y ningún otro predictor alcanzó este nivel de significancia cuando se añadió a la ecuación. La Tabla A.3 muestra las variables incluidas en la ecuación de regresión (\(R^2 = 0.612\)).
Tabla A.3. Factores que Afectan la Evaluación de la Calidad Gráfica, Estudio de Harbert
\[ \small{ \begin{array}{ll} \hline \text{Variables con} & \text{Variables con}\\ \text{Coeficientes Positivos} & \text{Coeficientes Negativos} \\ \hline\text{ Proporción de tinta de datos} & \text{Proporción de la página utilizada por el gráfico}\\ \text{Comparaciones facilitadas} &\text{Etiquetas verticales en el eje Y} \\ \text{Datos suficientes para} &\text{Uso de abreviaturas} \\ ~~~~\text{un gráfico rico}& \text{Uso de arte óptico} \\ &\text{Comparaciones usando áreas o volúmenes} \\ \hline \end{array} } \]
La proporción de tinta de datos fue definida por Tufte (1983, p. 93) como la “proporción de tinta del gráfico dedicada a la representación no redundante de la información de datos” o, equivalentemente, como “1.0 menos la proporción de un gráfico que puede borrarse sin pérdida de información de datos”. La proporción de tinta de datos es más fácil de calcular que la medida de densidad de datos definida en la Sección 21.3 de este documento. El arte óptico es decoración que no le dice al espectador nada nuevo.
Una variable que se había anticipado como muy significativa era la densidad de datos, que es difícil y requiere mucho tiempo para medir. Un hallazgo importante del estudio fue que la proporción de tinta de datos, más fácil de medir, y la proporción de página fueron suficientes para predecir las calificaciones. Una cita de la tesis de Harbert resume el hallazgo: “Las calificaciones más altas se otorgaron a aquellos gráficos que ocupan pequeñas proporciones de la página, tienen una alta proporción de tinta de datos, facilitan las comparaciones, tienen suficientes puntos de datos, tienen etiquetas impresas horizontalmente, no tienen abreviaturas, no tienen arte óptico y no utilizan comparaciones de volumen o en 3D” (Harbert 1995, p. 56).
Como un pequeño estudio de seguimiento al trabajo de Harbert, examinamos cada uno de los 19 gráficos no tabulares en el Life Insurance Fact Book (1994), evaluándolos en siete factores negativos. La Tabla A.4 muestra el porcentaje de gráficos que exhibieron cada uno de los factores negativos.
Tabla A.4. Porcentaje de Gráficos que Muestran Factores Negativos en Life Insurance Fact Book 1994
\[ \small{ \begin{array}{lc} \hline \text{Factor Negativo} &\text{Porcentaje} \\ & \text{de Gráficos} \\ \hline \text{Uso de barras en 3-D} & 79 \\ \text{Líneas de cuadrícula demasiado densas} &79 \\ \text{Dificultad para comparar valores de series temporales} &37\\ \text{Uso de barras apiladas} & 37 \\ \text{Crecimiento representado de manera pobre} &32\\ \text{Uso de líneas más anchas de lo necesario} & 16\\ \text{Uso de gráficos circulares} &5\\ \hline \end{array} } \]
Nuestra revisión sugiere que cada gráfico podría haberse reducido en un 50% a 75% sin pérdida de claridad. Esta observación está en línea con el hallazgo de Harbert sobre la variable de proporción de página. En resumen, los gráficos en el Life Insurance Fact Book podrían haberse producido de manera mucho más eficaz. Hacerlo mejoraría la calidad de la comunicación y potencialmente incrementaría el respeto con el que profesionales informados de otros campos ven a la industria aseguradora.
Esperamos que otros investigadores lleven a cabo estudios adicionales sobre la práctica gráfica en publicaciones actuariales. Al utilizar datos de tales estudios, la profesión puede mejorar sus prácticas, haciendo las comunicaciones más eficientes y precisas.
21.5 Observaciones Finales
El lema de la Sociedad de Actuarios es una cita de Ruskin: “El trabajo de la ciencia es sustituir hechos por apariencias y demostraciones por impresiones.” Armados con las pautas descritas en este capítulo y discutidas en las referencias, los actuarios pueden ser líderes en la presentación de datos de manera gráfica, sustituyendo demostraciones por impresiones. Encuestas de literatura actuarial reciente deberían ser la base para evaluar la práctica actual. Los editores y revisores de publicaciones profesionales pueden ser especialmente influyentes para lograr una mejora rápida en los estándares de práctica. Además, los actuarios pueden recomendar y usar libros de texto estadísticos que presten atención a la calidad gráfica.
Como los actuarios leen material que contiene gráficos, son consumidores. ¡Deben convertirse en consumidores exigentes! Muy a menudo, los valores predeterminados en el software de hojas de cálculo y gráficos estadísticos se convierten en la norma. Los actuarios no deberían permitir que las decisiones tomadas por los programadores de software determinen la calidad o los estándares gráficos. Aunque es fácil crear gráficos usando los valores predeterminados del software gráfico, los gráficos resultantes rara vez son completamente satisfactorios. Si un gráfico no vale la pena hacerlo bien, dejémoslo fuera de nuestras publicaciones.
21.6 Lecturas Adicionales y Referencias
Además de las referencias enumeradas, existen otros recursos disponibles para los actuarios interesados en mejorar sus habilidades en diseño gráfico. Al igual que la Sociedad de Actuarios, otra organización profesional, la American Statistical Association (ASA), tiene secciones de interés especial. En particular, la ASA ahora tiene una sección sobre gráficos estadísticos. Los actuarios interesados pueden unirse a la ASA y a esa sección para recibir el boletín Statistical Computing & Graphics. Esta publicación contiene ejemplos de prácticas gráficas excelentes en el contexto de descubrimientos y aplicaciones científicas. La revista técnica Journal of Computational and Graphical Statistics contiene información más detallada sobre gráficos efectivos.
Referencias del Capítulo
- American Council of Life Insurance. Various years. Life Insurance Fact Book. Washington, D.C.: ACLI.
- Cleveland, William S. (1994). The Elements of Graphing Data. Monterey, Calif.: Wadsworth.
- Cleveland, William S. (1993). Visualizing Data. Summit, N.J.: Hobart Press.
- Cleveland, William S., Diaconis, P., and McGill. R. (1982). Variables on scatterplots look more highly correlated when the scales are increased. Science 216, 1138-1141.
- Cleveland, William S., and McGill, R. (1984). Graphical perception: Theory, experimentation, and application to the development of graphical methods. Journal of the American Statistical Association 79, 531-454.
- Cleveland, William S., and McGill, R. (1985). Graphical perception and graphical methods for analyzing and presenting scientific data. Science 229, 828-833.
- Ehrenberg, A.S.C. (1977). Rudiments of Numeracy. Journal of the Royal Statistical Society A 140:277-97.
- Frees, Edward W. (1996). Data Analysis Using Regression Models. Englewood Cliffs, N.J.: Prentice Hall.
- Frees, Edward W. (1998). Relative Importance of Risk Sources in Insurance Systems, North American Actuarial Journal 2(2), 34-51.
- Frees, Edward W., Kung, Yueh C., Rosenberg, Marjorie A., Young, Virginia R., and Lai, Siu-Wai (1997). Forecasting Social Security Assumptions, North American Actuarial Journal 1(3), 49-82.
- Harbert, D. (1995). The Quality of Graphics in 1993 Psychology Journals, Senior honors thesis, University of Wisconsin-Madison.
- Huff, D. (1954). How To Lie with Statistics. New York: Norton.
- Schmid, C.F. (1992). Statistical Graphics: Design Principles and Practices Malabar, Fla.: Krieger Publishing Co.
- Schmit, Joan T., and Roth, K. (1990). Cost Effectiveness of Risk Management Practices, Journal of Risk and Insurance 57, 455-470.
- Strunk, W., and White, E.B. (1979). The Elements of Style. 3rd ed. New York: Macmillan.
- Tufte, Edward R. (1983). The Visual Display of Quantitative Information. Cheshire, Conn.: Graphics Press.
- Tufte, Edward R. (1990). Envisioning Information. Cheshire, Conn.: Graphics Press.
- Tufte, Edward R. (1997). Visual Explanations. Cheshire, Conn.: Graphics Press.
- Tukey, John (1977). Exploratory Data Analysis. Reading, Mass.: Addison-Wesley.
- University of Chicago Press (1993). The Chicago Manual of Style. 14th ed. Chicago, Ill.
Notas al Pie
Este capítulo se basa en “Designing Effective Graphs,” por Edward W. Frees y Robert B. Miller, 1990, North American Actuarial Journal, volumen 2, número 2, 53-70. Publicado por la Society of Actuaries - reproducido con permiso.↩︎
El código gráfico utiliza fragmentos pequeños de datos que pueden ser accedidos desde el libro Statistical Software Scripts.↩︎