Chapter 3 Regresión Lineal Múltiple - I

Vista previa del capítulo. Este capítulo introduce la regresión lineal en el caso de varios variables explicativas, conocida como regresión lineal múltiple. Muchos conceptos básicos de la regresión lineal se extienden directamente, incluyendo medidas de bondad de ajuste como $R^2$ y la inferencia usando estadísticas $t$. Los modelos de regresión lineal múltiple proporcionan un marco para resumir datos altamente complejos y multivariados. Debido a que este marco solo requiere linealidad en los parámetros, podemos ajustar modelos que son funciones no lineales de las variables explicativas, proporcionando así un amplio alcance de aplicaciones potenciales.

3.1 Método de Mínimos Cuadrados

El Capítulo 2 trató sobre el problema de una respuesta que depende de una sola variable explicativa. Ahora extendemos el enfoque de ese capítulo y estudiamos cómo una respuesta puede depender de varias variables explicativas.

Ejemplo: Seguro de Vida Temporal. Como todas las empresas, las compañías de seguros de vida buscan continuamente nuevas formas de llevar productos al mercado. Aquellos involucrados en el desarrollo de productos desean saber “¿quién compra seguro y cuánto compran?” En economía, esto se conoce como el lado de la demanda de un mercado de productos. Los analistas pueden obtener fácilmente información sobre las características de los clientes actuales a través de las bases de datos de la empresa. Los clientes potenciales, aquellos que no tienen seguro con la compañía, son a menudo el principal objetivo para expandir la cuota de mercado.

En este ejemplo, examinamos la Encuesta de Finanzas del Consumidor (SCF), una muestra representativa a nivel nacional que contiene información extensa sobre activos, pasivos, ingresos y características demográficas de los encuestados (potenciales clientes en EE. UU.). Estudiamos una muestra aleatoria de 500 hogares con ingresos positivos que fueron entrevistados en la encuesta de 2004. Inicialmente, consideramos el subconjunto de $n=275$ familias que compraron seguro de vida temporal. Deseamos abordar la segunda parte de la pregunta de la demanda y determinar las características de la familia que influyen en la cantidad de seguro comprado. El Capítulo 11 considerará la primera parte, es decir, si un hogar compra o no un seguro, a través de modelos donde la respuesta es una variable aleatoria binaria.

Para el seguro de vida temporal, la cantidad de seguro se mide por el valor nominal de la póliza, FACE, la cantidad que la compañía pagará en caso de la muerte del asegurado. Las características que resultarán importantes incluyen los ingresos anuales, INCOME, el número de años de EDUCATION del encuestado y el número de miembros del hogar, NUMHH.

En general, consideraremos conjuntos de datos donde hay $k$ variables explicativas y una variable de respuesta en una muestra de tamaño $n$. Es decir, los datos consisten en:

\[ \left\{ \begin{aligned} x_{11},x_{12},\ldots,x_{1k},y_1 \\ x_{21},x_{22},\ldots,x_{2k},y_2 \\ \vdots \\ x_{n1},x_{n2},\ldots,x_{nk},y_n \end{aligned} \right\}. \]

La $i$-ésima observación corresponde a la $i$-ésima fila, que consiste en $(x_{i1},x_{i2},\ldots,x_{ik},y_i)$. Para este caso general, tomamos $k+1$ mediciones en cada entidad. Para el ejemplo de demanda de seguros, $k=3$ y los datos consisten en $(x_{11},x_{12},x_{13}, y_1), \ldots , (x_{275,1},x_{275,2},x_{275,3},y_{275})$. Es decir, usamos cuatro mediciones de cada uno de los $n=275$ hogares.

Resumiendo los Datos

Comenzamos el análisis de los datos examinando cada variable por separado. La Tabla 3.1 proporciona estadísticas descriptivas básicas de las cuatro variables. Para FACE e INCOME, vemos que la media es mucho mayor que la mediana, lo que sugiere que la distribución está sesgada hacia la derecha. Los histogramas (no reportados aquí) muestran que este es el caso. Será útil considerar también sus transformaciones logarítmicas, LNFACE y LNINCOME, respectivamente, que también se informan en la Tabla 3.1.

Tabla 3.1: **Estadísticas Descriptivas del Seguro de Vida Temporal**
	Media	Mediana	Desviación Estándar	Mínimo	Máximo
FACE	747,581	150,000	1,674,362	800	14,000,000
INCOME	208,975	65,000	824,010	260	10,000,000
EDUCATION	14.524	16	2.549	2	17
NUMHH	2.96	3	1.493	1	9
LNFACE	11.99	11.918	1.871	6.685	16.455
LNINCOME	11.149	11.082	1.295	5.561	16.118

El siguiente paso es medir la relación entre cada $x$ sobre $y$, comenzando con los diagramas de dispersión en la Figura 3.1. El panel de la izquierda es un gráfico de FACE versus INCOME; en este panel, vemos una gran concentración en la esquina inferior izquierda que corresponde a hogares con ingresos y cantidades de seguro pequeños. Ambas variables tienen distribuciones sesgadas y su efecto conjunto es altamente no lineal. El panel derecho presenta las mismas variables, pero utilizando transformaciones logarítmicas. Aquí, vemos una relación que se puede aproximar más fácilmente con una línea.

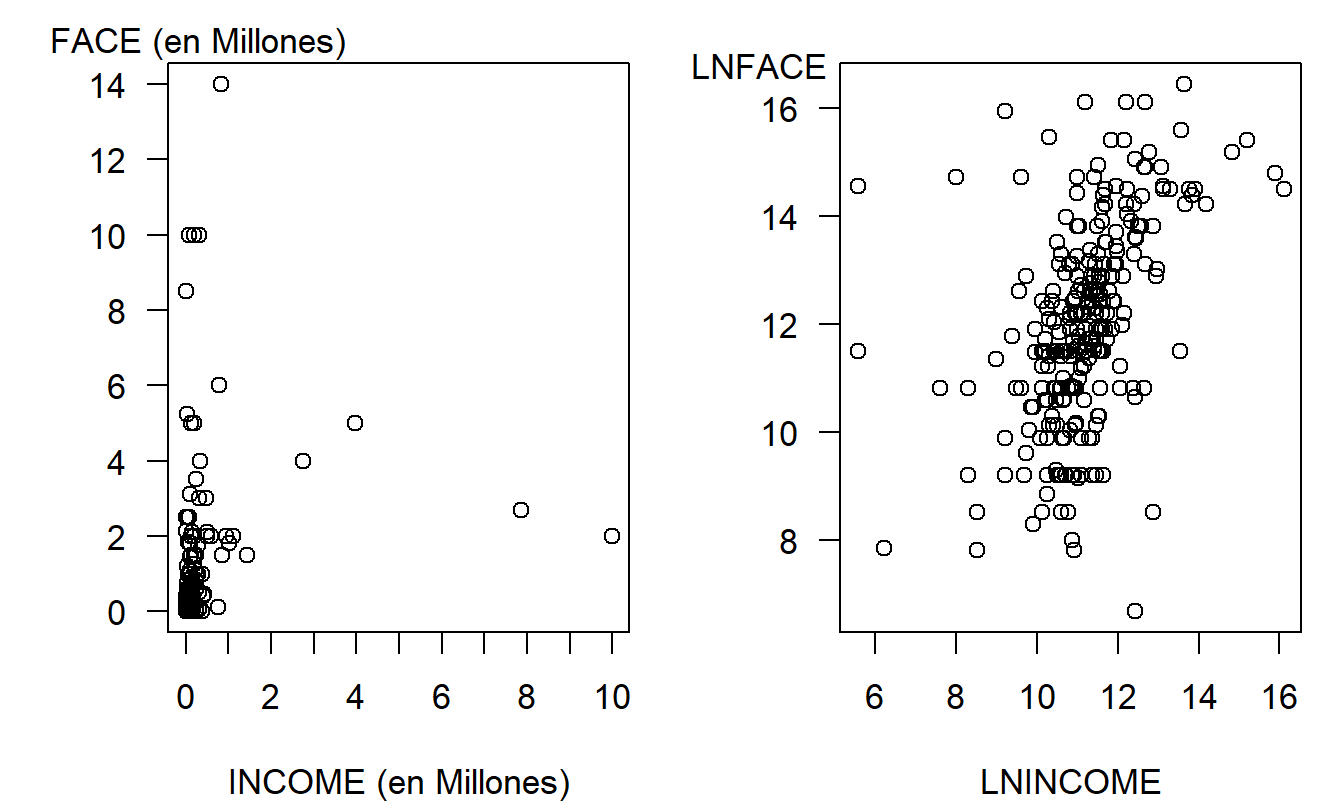
Ingresos versus Monto Nominal del Seguro de Vida Temporal. El panel de la izquierda es un gráfico de monto nominal versus ingresos, mostrando un patrón altamente no lineal. En el panel derecho, el monto nominal versus ingresos está en unidades logarítmicas naturales, sugiriendo un patrón lineal (aunque variable).

Figura 3.1: Ingresos versus Monto Nominal del Seguro de Vida Temporal. El panel de la izquierda es un gráfico de monto nominal versus ingresos, mostrando un patrón altamente no lineal. En el panel derecho, el monto nominal versus ingresos está en unidades logarítmicas naturales, sugiriendo un patrón lineal (aunque variable).

Código R para producir la Tabla 3.1 y la Figura 3.1

Term <- read.csv("CSVData/TermLife.csv", header=TRUE)
#  SELECCIONAR EL SUBCONJUNTO DE DATOS CORRESPONDIENTE A LA COMPRA DE SEGURO
Term2  <-subset(Term, FACE > 0)
#  TABLA 3.1 ESTADÍSTICAS DESCRIPTIVAS
BookSummStats <- function(Xymat){
meanSummary <- sapply(Xymat, mean,  na.rm=TRUE) 
sdSummary   <- sapply(Xymat, sd,    na.rm=TRUE) 
minSummary  <- sapply(Xymat, min,   na.rm=TRUE) 
maxSummary  <- sapply(Xymat, max,   na.rm=TRUE) 
medSummary  <- sapply(Xymat, median,na.rm=TRUE) 
tableMat  <- cbind(meanSummary, medSummary, sdSummary, minSummary, maxSummary)
return(tableMat)
}

LNFACE <- log(Term2$FACE)
LNINCOME <- log(Term2$INCOME)

Xymat <- data.frame(cbind(Term2$FACE,
Term2$INCOME,Term2$EDUCATION, Term2$NUMHH,LNFACE, LNINCOME) ) 
tableMat  <- BookSummStats(Xymat)

colnames(tableMat)  <- c("Media" , "Mediana" , "Desviación Estándar" , 
                         "Mínimo" , "Máximo")
rownames(tableMat)  <- c("FACE", "INCOME", "EDUCATION", "NUMHH",
                         "LNFACE", "LNINCOME")
tableMat1 <- tableMat
tableMat1[3:6,]  <- round(tableMat1[3:6,], digits = 3)
tableMat1[1:2,] <- format(round(tableMat[1:2,], digits=0), big.mark = ',')


TableGen1(TableData=tableMat1, 
         TextTitle='Estadísticas Descriptivas del Seguro de Vida Temporal', 
         Align='r', Digits=3, ColumnSpec=1:5,
         ColWidth = ColWidth5)

Term <- read.csv("CSVData/TermLife.csv", header=TRUE)
#  SELECCIONAR EL SUBCONJUNTO DE DATOS CORRESPONDIENTE A LA COMPRA DE SEGURO
Term2  <-subset(Term, FACE > 0)
Term2$LNFACE <- log(Term2$FACE)
Term2$LNINCOME <- log(Term2$INCOME)
#  FIGURA 3.1
par(mfrow=c(1, 2), cex=1.1, mar=c(4.1,4,1.5,1))
plot(Term2$INCOME, Term2$FACE, ylab="", las=1, yaxt="n", xaxt="n", xlab="INCOME (en Millones)")
mtext("FACE (en Millones)", side=2, at=15200000, las=1, cex=1.1, adj=.4)
axis(2,at=seq(0,14000000,2000000), labels=c("0", "2", 
    "4", "6", "8","10","12","14"), las=1)
axis(1,at=seq(0,11000000,1000000), labels=c("0","1", "2","3

", 
    "4","5", "6","7","8","9","10","11"))
plot(Term2$LNINCOME, Term2$LNFACE, ylab="", xlab = "LNINCOME", las=1)
mtext("LNFACE", side=2, at=16.8, las=1, cex=1.1, adj=1.1)

Los datos de Seguro de Vida Temporal son multivariados en el sentido de que se toman varias mediciones en cada hogar. Es difícil producir un gráfico de observaciones en tres o más dimensiones en una plataforma bidimensional, como una hoja de papel, que no sea confuso, engañoso o ambos. Para resumir gráficamente datos multivariados en aplicaciones de regresión, considere usar una matriz de diagramas de dispersión como en la Figura 3.2. Cada cuadrado de esta figura representa un gráfico simple de una variable contra otra. Para cada cuadrado, la variable de la fila da las unidades del eje vertical y la variable de la columna da las unidades del eje horizontal. La matriz a veces se llama una matriz de dispersión parcial porque solo se presentan los elementos en la parte inferior izquierda.

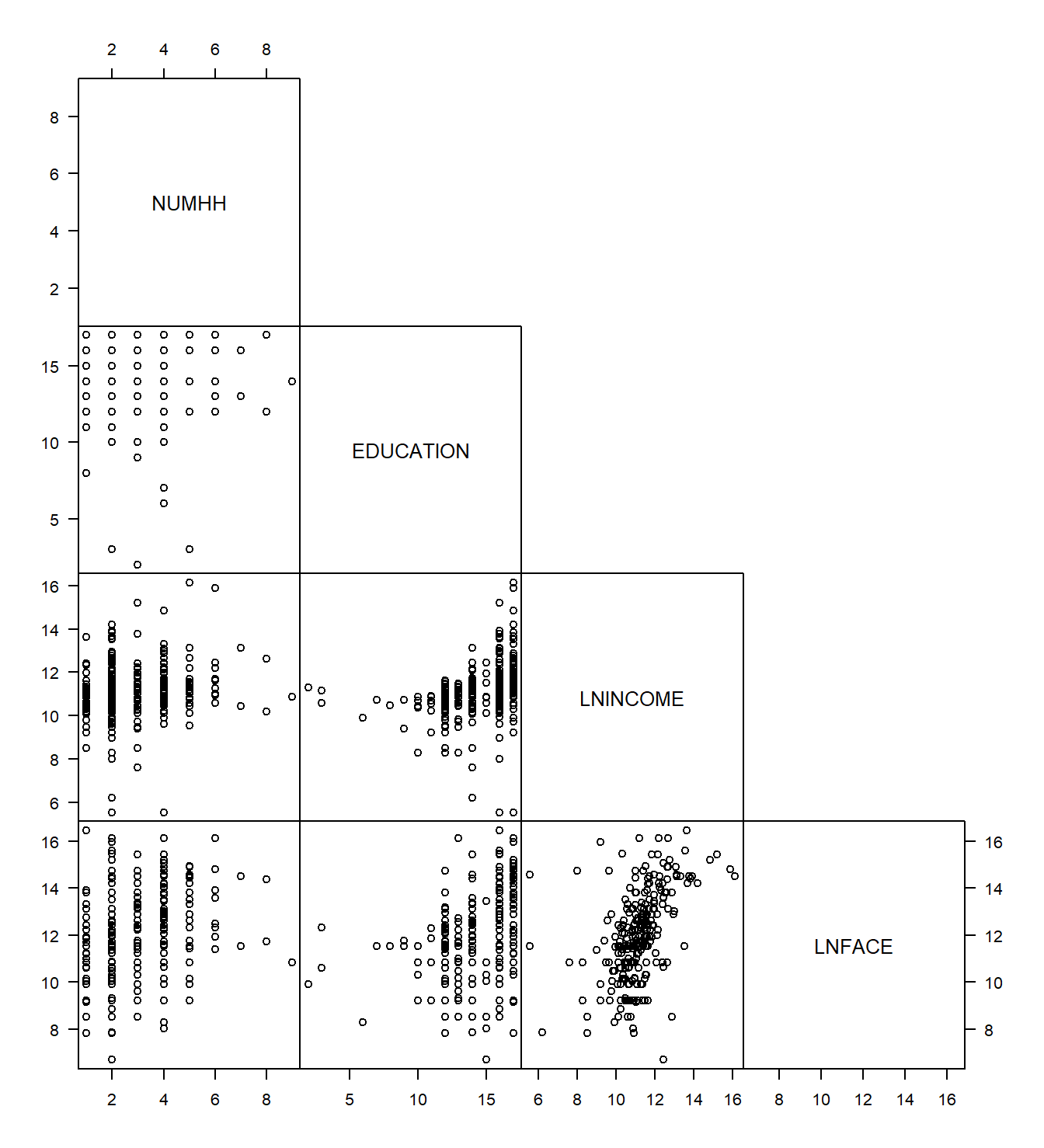
Figura 3.2: Matriz de diagramas de dispersión de cuatro variables. Cada cuadrado es un diagrama de dispersión.

La matriz de diagramas de dispersión se puede resumir numéricamente usando una matriz de correlación. Cada correlación en la Tabla 3.2 corresponde a un cuadrado de la matriz de diagramas de dispersión en la Figura 3.2. Los analistas a menudo presentan tablas de correlaciones porque son fáciles de interpretar. Sin embargo, recuerde que un coeficiente de correlación solo mide la magnitud de las relaciones lineales. Por lo tanto, una tabla de correlaciones proporciona una idea de las relaciones lineales, pero puede pasar por alto una relación no lineal que se puede revelar en una matriz de diagramas de dispersión.

Tabla 3.2: **Correlaciones del Seguro de Vida Temporal**
	NUMHH	EDUCATION	LNINCOME
EDUCATION	-0.064
LNINCOME	0.179	0.343
LNFACE	0.288	0.383	0.482

La matriz de diagramas de dispersión y la correspondiente matriz de correlación son herramientas útiles para resumir datos multivariados. Son fáciles de producir e interpretar. Sin embargo, cada una captura solo relaciones entre pares de variables y no puede cuantificar relaciones entre varias variables.

Código R para producir la Tabla 3.2 y la Figura 3.2

Método de Mínimos Cuadrados

Consideremos la pregunta: “¿Puede el conocimiento de la educación, el tamaño del hogar y el ingreso ayudarnos a entender la demanda de seguros?” Las correlaciones en la Tabla 3.2 y los gráficos en las Figuras 3.1 y 3.2 sugieren que cada variable, EDUCATION, NUMHH y LNINCOME, puede ser una variable explicativa útil de LNFACE cuando se consideran individualmente. Parece razonable investigar el efecto conjunto de estas variables en una respuesta.

El concepto geométrico de un plano se utiliza para explorar la relación lineal entre una respuesta y varias variables explicativas. Recuerde que un plano extiende el concepto de una línea a más de dos dimensiones. Un plano puede definirse mediante una ecuación algebraica como

\[ y = b_0 + b_1 x_1 + \ldots + b_k x_k. \]

Esta ecuación define un plano en $k+1$ dimensiones. La Figura 3.3 muestra un plano en tres dimensiones. En esta figura, hay una variable de respuesta, LNFACE, y dos variables explicativas, EDUCATION y LNINCOME (NUMHH se mantiene fijo). Es difícil graficar más de tres dimensiones de una manera significativa.

Figura 3.3: Un ejemplo de un plano tridimensional

Necesitamos una manera de determinar un plano basado en los datos. La dificultad es que en la mayoría de las aplicaciones de análisis de regresión, el número de observaciones, $n$, excede con creces el número de observaciones requeridas para ajustar un plano, $k+1$. Por lo tanto, generalmente no es posible encontrar un solo plano que pase por todas las $n$ observaciones. Como en el Capítulo 2, utilizamos el método de mínimos cuadrados para determinar un plano a partir de los datos.

El método de mínimos cuadrados se basa en determinar los valores de $b_0^{\ast},b_1^{\ast},\ldots,b_k^{\ast}$ que minimizan la cantidad

\[\begin{equation} SS(b_0^{\ast},b_1^{\ast},\ldots,b_k^{\ast})=\sum_{i=1}^{n}\left( y_i-\left( b_0^{\ast}+b_1^{\ast}x_{i1}+\ldots+b_k^{\ast}x_{ik}\right) \right) ^2. \tag{3.1} \end{equation}\]

Dejamos de usar la notación con asterisco, o estrella, y usamos $b_0, b_1, \ldots, b_k$ para denotar los mejores valores, conocidos como las estimaciones de mínimos cuadrados. Con las estimaciones de mínimos cuadrados, definimos el plano de regresión de mínimos cuadrados, o ajustado, como

\[ \widehat{y} = b_0 + b_1 x_1 + \ldots + b_k x_k. \]

Las estimaciones de mínimos cuadrados se determinan minimizando $SS(b_0^{\ast},b_1^{\ast},\ldots,b_k^{\ast})$. Es difícil escribir los estimadores de mínimos cuadrados resultantes utilizando una fórmula simple a menos que se recurra a la notación matricial. Debido a su importancia en los modelos estadísticos aplicados, se proporciona una fórmula explícita para los estimadores a continuación. Sin embargo, estas fórmulas han sido programadas en una gran variedad de paquetes de software estadístico y de hojas de cálculo. La disponibilidad de estos paquetes permite a los analistas de datos concentrarse en las ideas del procedimiento de estimación en lugar de enfocarse en los detalles de los procedimientos de cálculo.

Como ejemplo, se ajustó un plano de regresión a los datos de Seguro de Vida Temporal donde se utilizaron tres variables explicativas, $x_1$ para EDUCATION, $x_2$ para NUMHH y $x_3$ para LNINCOME. El plano de regresión ajustado resultante es

\[\begin{equation} \widehat{y} = 2.584 + 0.206 x_1 + 0.306 x_2 + 0.494 x_3. \tag{3.2} \end{equation}\]

Notación Matricial

Supongamos que los datos son de la forma $(x_{i0}, x_{i1}, \ldots, x_{ik}, y_i)$, donde $i = 1, \ldots, n$. Aquí, la variable $x_{i0}$ está asociada con el término “intercepto”. En la mayoría de las aplicaciones, suponemos que $x_{i0}$ es idénticamente igual a 1 y, por lo tanto, no es necesario representarlo explícitamente. Sin embargo, hay aplicaciones importantes donde este no es el caso, y por lo tanto, para expresar el modelo en notación general, se incluye aquí. Los datos se representan en notación matricial usando:

\[ \mathbf{y} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} ~~~~ \mathbf{X} = \begin{pmatrix} x_{10} & x_{11} & \cdots & x_{1k} \\ x_{20} & x_{21} & \cdots & x_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n0} & x_{n1} & \cdots & x_{nk} \end{pmatrix}. \]

Aquí, $\mathbf{y}$ es el vector de respuestas de $n \times 1$ y $\mathbf{X}$ es la matriz de variables explicativas de $n \times (k+1)$. Usamos la convención de álgebra matricial de que las letras minúsculas y mayúsculas en negrita representan vectores y matrices, respectivamente. (Si necesita repasar sobre matrices, revise la Sección 2.11).

Ejemplo: Seguro de Vida Temporal - Continuación. Recuerde que $y$ representa el valor logarítmico del seguro, $x_1$ para los años de educación, $x_2$ para el número de miembros del hogar, y $x_3$ para el ingreso logarítmico. Por lo tanto, hay $k = 3$ variables explicativas y $n = 275$ hogares. El vector de respuestas y la matriz de variables explicativas son:

\[ \small{ \mathbf{y} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_{275} \end{pmatrix} = \begin{pmatrix} 9.904 \\ 11.775 \\ \vdots \\ 9.210 \end{pmatrix} \\ \mathbf{X} = \begin{pmatrix} 1 & x_{11} & x_{12} & x_{13} \\ 1 & x_{21} & x_{22} & x_{23} \\ \vdots & \vdots & \vdots & \vdots \\ 1 & x_{275,1} & x_{275,2} & x_{275,3} \end{pmatrix} = \begin{pmatrix} 1 & 16 & 3 & 10.669 \\ 1 & 9 & 3 & 9.393 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & 12 & 1 & 10.545 \end{pmatrix}. } \]

Por ejemplo, para la primera observación en el conjunto de datos, la variable dependiente es $y_1 = 9.904$ (correspondiente a $\exp(9.904) = \$20,000$), para un encuestado con 16 años de educación que vive en un hogar con 3 personas y un ingreso logarítmico de 10.669 ($\exp(10.669) = \$43,000$).

Bajo el principio de estimación de mínimos cuadrados, nuestro objetivo es elegir los coeficientes $b_0^{\ast}, b_1^{\ast}, \ldots, b_k^{\ast}$ para minimizar la función de suma de cuadrados $SS(b_0^{\ast}, b_1^{\ast}, \ldots, b_k^{\ast})$. Usando cálculo, regresamos a la ecuación (3.1), tomamos derivadas parciales con respecto a cada coeficiente y establecemos estas cantidades igual a cero:

\[ \begin{array}{ll} \frac{\partial }{\partial b_j^{\ast}}SS(b_0^{\ast}, b_1^{\ast}, \ldots, b_k^{\ast}) &= \sum_{i=1}^{n}\left( -2x_{ij}\right) \left( y_i-\left( b_0^{\ast}+b_1^{\ast}x_{i1}+\ldots+b_k^{\ast}x_{ik}\right) \right) \\ &= 0, ~~~ \text{para} ~ j=0,1,\ldots,k. \end{array} \]

Este es un sistema de $k+1$ ecuaciones y $k+1$ incógnitas que se puede resolver fácilmente usando notación matricial, como sigue.

Podemos expresar el vector de parámetros a minimizar como $\mathbf{b}^{\ast}=(b_0^{\ast}, b_1^{\ast}, \ldots, b_k^{\ast})^{\prime}$. Usando esto, la suma de cuadrados se puede escribir como $SS(\mathbf{b}^{\ast}) = (\mathbf{y-Xb}^{\ast})^{\prime}(\mathbf{y-Xb}^{\ast})$. Así, en forma matricial, la solución al problema de minimización se puede expresar como $\frac{\partial}{\partial \mathbf{b}^{\ast}} SS(\mathbf{b}^{\ast}) = \mathbf{0}$. Esta solución satisface las ecuaciones normales:

\[\begin{equation} \mathbf{X^{\prime}Xb} = \mathbf{X}^{\prime}\mathbf{y}. \tag{3.3} \end{equation}\]

Aquí, se ha eliminado la notación de asterisco (*) para denotar el hecho de que $\mathbf{b} = (b_0, b_1, \ldots, b_k)^{\prime}$ representa el mejor vector de valores en el sentido de minimizar $SS(\mathbf{b}^{\ast})$ sobre todas las opciones de $\mathbf{b}^{\ast}$.

El estimador de mínimos cuadrados $\mathbf{b}$ no necesita ser único. Sin embargo, suponiendo que las variables explicativas no son combinaciones lineales entre sí, tenemos que $\mathbf{X^{\prime}X}$ es invertible. En este caso, podemos escribir la solución única como:

\[\begin{equation} \mathbf{b} = \left( \mathbf{X^{\prime}X} \right)^{-1} \mathbf{X}^{\prime} \mathbf{y}. \tag{3.4} \end{equation}\]

Para ilustrar, para el ejemplo de Seguro de Vida Temporal, la ecuación (3.4) produce:

\[ \small{ \mathbf{b} = \begin{pmatrix} b_0 \\ b_1 \\ b_2 \\ b_3 \\ \end{pmatrix} = \begin{pmatrix} 2.584 \\ 0.206 \\ 0.306 \\ 0.494 \\ \end{pmatrix}. } \]

3.2 Modelo de Regresión Lineal y Propiedades de los Estimadores

En la sección anterior, aprendimos cómo utilizar el método de mínimos cuadrados para ajustar un plano de regresión con un conjunto de datos. Esta sección describe los supuestos que sustentan el modelo de regresión y algunas de las propiedades resultantes de los estimadores de los coeficientes de regresión. Con el modelo y los datos ajustados, podremos hacer inferencias sobre el conjunto de datos de la muestra a una población más grande. Además, más adelante utilizaremos estos supuestos del modelo de regresión para ayudarnos a mejorar la especificación del modelo en el Capítulo 5.

3.2.1 Función de Regresión

La mayoría de los supuestos del modelo de regresión lineal múltiple se trasladarán directamente de los supuestos del modelo de regresión lineal básico introducidos en la Sección 2.2. La principal diferencia es que ahora resumimos la relación entre la variable respuesta y las variables explicativas a través de la función de regresión:

\[\begin{equation} \mathrm{E~}y = \beta_0 x_0 + \beta_1 x_1 + \ldots + \beta_k x_k, \tag{3.5} \end{equation}\]

que es lineal en los parámetros $\beta_0,\ldots,\beta_k$. De aquí en adelante, usaremos $x_0 = 1$ para la variable asociada con el parámetro $\beta_0$; esto es lo predeterminado en la mayoría de los paquetes estadísticos, y la mayoría de las aplicaciones de regresión incluyen el término de intercepto $\beta_0$. El intercepto es el valor esperado de $y$ cuando todas las variables explicativas son iguales a cero. Aunque rara vez es de interés, el término $\beta_0$ sirve para establecer la altura del plano de regresión ajustado.

En cambio, los otros betas son típicamente parámetros importantes en un estudio de regresión. Para ayudar a interpretarlos, inicialmente asumimos que $x_j$ varía de manera continua y no está relacionado con las otras variables explicativas. Entonces, podemos interpretar $\beta_j$ como el cambio esperado en $y$ por unidad de cambio en $x_j$ asumiendo que todas las demás variables explicativas se mantienen fijas. Es decir, desde el cálculo, reconocerás que $\beta_j$ puede interpretarse como una derivada parcial. Específicamente, usando la ecuación anterior, tenemos que

\[ \beta_j = \frac{\partial }{\partial x_j}\mathrm{E}~y. \]

3.2.2 Interpretación del Coeficiente de Regresión

Examinemos las estimaciones de los coeficientes de regresión del ejemplo de Seguro de Vida Temporal y enfoquémonos inicialmente en el signo de los coeficientes. Por ejemplo, en la ecuación (3.4), el coeficiente asociado con NUMHH es $b_2 = 0.306 > 0$. Si consideramos dos hogares que tienen el mismo ingreso y el mismo nivel de educación, entonces se espera que el hogar más grande (en términos de NUMHH) demande más seguro de vida temporal bajo el modelo de regresión. Esta es una interpretación sensata; los hogares más grandes tienen más dependientes para los cuales el seguro de vida temporal puede proporcionar activos financieros necesarios en caso de la muerte prematura de un sostén de la familia. El coeficiente positivo asociado con el ingreso ($b_3 = 0.494$) también es plausible; los hogares con mayores ingresos tienen más dinero disponible para comprar seguros. El signo positivo asociado con EDUCATION ($b_1 = 0.206)$ también es razonable; más educación sugiere que los encuestados son más conscientes de sus necesidades de seguro, otras cosas iguales.

También necesitas interpretar la cantidad del coeficiente de regresión. Consideremos primero el coeficiente de EDUCATION. Usando la ecuación (3.4), se calcularon los valores ajustados de $\widehat{\mathrm{LNFACE}}$ permitiendo que EDUCATION variara y manteniendo NUMHH y LNINCOME fijos en los promedios de la muestra. Los resultados son:

Efectos de Pequeños Cambios en la Educación

EDUCATION	14	14.1	14.2	14.3
$\widehat{\mathit{LNFACE}}$	11.883	11.904	11.924	11.945
$\widehat{\mathit{FACE}}$	144,803	147,817	150,893	154,034
$\widehat{\mathit{FACE}}$ % Cambio		2.081	2.081	2.081

A medida que EDUCATION aumenta, $\widehat{\mathrm{LNFACE}}$ también aumenta. Además, la cantidad de incremento en $\widehat{\mathrm{LNFACE}}$ es un 0.0206 constante. Esto viene directamente de la ecuación (3.4); a medida que EDUCATION aumenta en 0.1 años, se espera que la demanda de seguros aumente en 0.0206 dólares logarítmicos, manteniendo NUMHH y LNINCOME fijos. Esta interpretación es correcta, pero la mayoría de los directores de desarrollo de productos no son muy partidarios de los dólares logarítmicos. Para volver a dólares, los valores ajustados pueden calcularse a través de la exponenciación como $\widehat{\mathrm{FACE}} = \exp(\widehat{\mathrm{LNFACE}})$. Además, se puede calcular el cambio porcentual; por ejemplo, $100 \times (147,817/144,803 - 1) \approx 2.08\%$.

Esto proporciona otra interpretación del coeficiente de regresión; a medida que EDUCATION aumenta en 0.1 años, se espera que la demanda de seguros aumente en un 2.08%. Esta es una simple consecuencia del cálculo usando $\partial \ln y / \partial x = \left(\partial y / \partial x \right) / y$; es decir, un pequeño cambio en el valor logarítmico de $y$ equivale a un pequeño cambio en $y$ como una proporción de $y$. Es debido a este resultado del cálculo que utilizamos logaritmos naturales en lugar de logaritmos comunes en el análisis de regresión. Dado que esta tabla utiliza un cambio discreto en EDUCATION, el 2.08% difiere ligeramente del resultado continuo $0.206 \times (\mathrm{cambio~en~EDUCATION}) = 2.06\%$. Sin embargo, esta proximidad generalmente se considera adecuada para fines de interpretación.

Continuando con esta lógica, consideremos pequeños cambios en el ingreso logarítmico.

Efectos de Pequeños Cambios en el Ingreso Logarítmico

LNINCOME	11	11.1	11.2	11.3
INCOME	59,874	66,171	73,130	80,822
INCOME % Cambio		10.52	10.52	10.52
$\widehat{\mathit{LNFACE}}$	11.957	12.006	12.055	12.105
$\widehat{\mathit{FACE}}$	155,831	163,722	172,013	180,724
$\widehat{\mathit{FACE}}$ % Cambio		5.06	5.06	5.06
$\widehat{\mathit{FACE}}$ % Cambio / INCOME % Cambio		0.482	0.482	0.482

Podemos usar la misma lógica para interpretar el coeficiente LNINCOME en la ecuación (3.4). A medida que el ingreso logarítmico aumenta en 0.1 unidades, se espera que la demanda de seguros aumente en un 5.06%. Esto se refiere a las unidades logarítmicas en $y$ pero no en $x$. Podemos usar la misma lógica para decir que a medida que el ingreso logarítmico aumenta en 0.1 unidades, el INCOME aumenta en un 10.52%. Por lo tanto, un cambio del 10.52% en el INCOME corresponde a un cambio del 5.06% en el FACE. Resumiendo, decimos que, manteniendo NUMHH y EDUCATION fijos, esperamos que un aumento del 1% en el INCOME esté asociado con un aumento del 0.482% en $\widehat{\mathrm{FACE}}$ (como antes, esto es cercano a la estimación del parámetro $b_3 = 0.494$). El coeficiente asociado con el ingreso se conoce como elasticidad en economía. En economía, la elasticidad es la relación entre el cambio porcentual en una variable y el cambio porcentual en otra variable. Matemáticamente, resumimos esto como:

\[ \frac{\partial \ln y}{\partial \ln x} = \left(\frac{\partial y}{y}\right)/\left(\frac{\partial x}{x}\right). \]

3.2.3 Suposiciones del Modelo

Como en la Sección 2.2 para una sola variable explicativa, existen dos conjuntos de suposiciones que se pueden utilizar para la regresión lineal múltiple. Son conjuntos equivalentes, cada uno con ventajas comparativas a medida que avanzamos en nuestro estudio de la regresión. La representación de “observables” se centra en las variables de interés $(x_{i1}, \ldots, x_{ik}, y_i)$. La “representación del error” proporciona una base para motivar nuestras medidas de bondad de ajuste y el estudio del análisis de residuales. Sin embargo, el segundo conjunto de suposiciones se centra en el caso de errores aditivos y oscurece la base de muestreo del modelo.

\[ \textbf{Suposiciones de Muestreo del Modelo de Regresión Lineal Múltiple} \\ \small{ \begin{array}{ll} \text{Representación de Observables} & \text{Representación de Error} \\ \hline F1.~ \mathrm{E}~y_i=\beta_0+\beta_1 x_{i1}+\ldots+\beta_k x_{ik}. & E1.~ y_i=\beta_0+\beta_1 x_{i1}+\ldots+\beta_k x_{ik}+\varepsilon_i. \\ F2.~ \{x_{i1},\ldots ,x_{ik}\} & E2.~ \{x_{i1},\ldots ,x_{ik}\} \\ \ \ \ \ \ \ \ \ \text{son variables no estocásticas.} & \ \ \ \ \ \ \ \ \text{son variables no estocásticas.} \\ F3.~ \mathrm{Var}~y_i=\sigma^2. & E3.~ \mathrm{E}~\varepsilon_i=0 \text{ y } \mathrm{Var}~\varepsilon_i=\sigma^2. \\ F4.~ \{y_i\} \text{ son variables aleatorias independientes.} & E4.~ \{\varepsilon_i\} \text{ son variables aleatorias independientes.} \\ F5.~ \{y_i\} \text{ están distribuidos normalmente.} & E5.~ \{\varepsilon_i\} \text{ están distribuidos normalmente.} \\ \hline \end{array} } \]

Para motivar aún más las Suposiciones F2 y F4, generalmente asumimos que nuestros datos han sido obtenidos como resultado de un esquema de muestreo estratificado, donde cada valor único de $\{x_{i1}, \ldots, x_{ik}\}$ se trata como un estrato. Es decir, para cada valor de $\{x_{i1}, \ldots, x_{ik}\}$, tomamos una muestra aleatoria de respuestas de una población. Así, las respuestas dentro de cada estrato son independientes entre sí, al igual que las respuestas de diferentes estratos. El Capítulo 6 discutirá esta base de muestreo en mayor detalle.

3.2.4 Propiedades de los Estimadores de los Coeficientes de Regresión

La Sección 3.1 describió el método de mínimos cuadrados para estimar los coeficientes de regresión. Con las suposiciones del modelo de regresión, podemos establecer algunas propiedades básicas de estos estimadores. Para hacerlo, de la Sección 2.11.4, tenemos que la esperanza de un vector es el vector de esperanzas, de modo que

\[ \small{ \mathrm{E}~\mathbf{y} = \left( \begin{array}{l} \mathrm{E}~y_1 \\ \mathrm{E}~y_2 \\ \vdots \\ \mathrm{E}~y_n \end{array} \right) . } \]

Además, la multiplicación básica de matrices muestra que

\[ \small{ \mathbf{X} \boldsymbol \beta = \left( \begin{array}{cccc} 1 & x_{11} & \cdots & x_{1k} \\ 1 & x_{21} & \cdots & x_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & \cdots & x_{nk} \end{array} \right) \left( \begin{array}{c} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_k \end{array} \right) = \left( \begin{array}{c} \beta_0 + \beta_1 x_{11} + \cdots + \beta_k x_{1k} \\ \beta_0 + \beta_1 x_{21} + \cdots + \beta_k x_{2k} \\ \vdots \\ \beta_0 + \beta_1 x_{n1} + \cdots + \beta_k x_{nk} \end{array} \right) . } \]

Dado que la $i$-ésima fila de la suposición F1 es $\mathrm{E}~y_i = \beta_0 + \beta_1 x_{i1} + \cdots + \beta_k x_{ik}$, podemos reescribir esta suposición en forma matricial como $\mathrm{E}~\mathbf{y} = \mathbf{X} \boldsymbol \beta$. Ahora estamos en condiciones de enunciar la primera propiedad importante de los estimadores de regresión por mínimos cuadrados.

Propiedad 1. Consideremos un modelo de regresión y que se cumplan las Suposiciones F1-F4. Entonces, el estimador $\mathbf{b}$ definido en la ecuación (3.4) es un estimador insesgado del vector de parámetros $\boldsymbol \beta$.

Para establecer la Propiedad 1, tenemos que

\[ \begin{array}{ll} \mathrm{E}~\mathbf{b} & = \mathrm{E}~\left((\mathbf{X^{\prime}X)}^{-1}\mathbf{X}^{\prime}\mathbf{y}\right) = (\mathbf{X^{\prime}X)}^{-1}\mathbf{X}^{\prime}\mathrm{E}~\mathbf{y} \\ &= (\mathbf{X^{\prime}X)}^{-1} \mathbf{X}^{\prime} \left( \mathbf{X} \boldsymbol \beta \right) = \boldsymbol \beta, \end{array} \]

utilizando reglas de multiplicación de matrices. Este capítulo asume que $\mathbf{X^{\prime}X}$ es invertible. También se puede mostrar que el estimador de mínimos cuadrados solo necesita ser una solución de las ecuaciones normales para ser insesgado (sin requerir que $\mathbf{X^{\prime}X}$ sea invertible, ver Sección 4.7.3). Así, se dice que $\mathbf{b}$ es un estimador insesgado de $\boldsymbol \beta$. En particular, $\mathrm{E}~b_j = \beta_j$ para $j = 0,1,\ldots,k$.

Dado que la independencia implica covarianza cero, de la Suposición F4 tenemos que $\mathrm{Cov}(y_i,y_j) = 0$ para $i \neq j$. A partir de esto, de la Suposición F3 y de la definición de la varianza de un vector, tenemos que

\[ \small{ \begin{array}{ll} \mathrm{Var~}\mathbf{y} &= \left( \begin{array}{cccc} \mathrm{Var~}y_1 & \mathrm{Cov}(y_1,y_2) & \cdots & \mathrm{Cov}(y_1,y_n) \\ \mathrm{Cov}(y_2,y_1) & \mathrm{Var~}y_2 & \cdots & \mathrm{Cov}(y_2,y_n) \\ \vdots & \vdots & \ddots & \vdots \\ \mathrm{Cov}(y_n,y_1) & \mathrm{Cov}(y_n,y_2) & \cdots & \mathrm{Var~}y_n \end{array} \right) \\ &= \left( \begin{array}{cccc} \sigma^2 & 0 & \cdots & 0 \\ 0 & \sigma^2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma^2 \end{array} \right) = \sigma^2 \mathbf{I}, \end{array} } \]

donde $\mathbf{I}$ es una matriz identidad de $n \times n$. Ahora estamos en condiciones de enunciar la segunda propiedad importante de los estimadores de regresión por mínimos cuadrados.

Propiedad 2. Consideremos un modelo de regresión y que se cumplan las Suposiciones F1-F4. Entonces, el estimador $\mathbf{b}$ definido en la ecuación (3.4) tiene una varianza de $\mathrm{Var~}\mathbf{b} = \sigma^2(\mathbf{X^{\prime}X)}^{-1}$.

Para establecer la Propiedad 2, a partir de la propiedad de la matriz de varianza, tenemos que

\[ \small{ \begin{array}{ll} \mathrm{Var~}\mathbf{b} & = \mathrm{Var~}\left((\mathbf{X^{\prime}X)}^{-1}\mathbf{X}^{\prime}\mathbf{y}\right) = (\mathbf{X^{\prime}X)}^{-1} \mathbf{X}^{\prime} \mathrm{Var~}\mathbf{y} \mathbf{X} (\mathbf{X^{\prime}X)}^{-1} \\ &= (\mathbf{X^{\prime}X)}^{-1} \mathbf{X}^{\prime} \sigma^2 \mathbf{I} \mathbf{X} (\mathbf{X^{\prime}X)}^{-1} = \sigma^2 (\mathbf{X^{\prime}X)}^{-1}, \end{array} } \]

como se requiere. Esta propiedad importante nos permitirá medir la precisión del estimador $\mathbf{b}$ cuando discutamos la inferencia estadística. Específicamente, por la definición de la varianza de un vector (ver Sección 2.11.4),

\[\begin{equation} \small{ \mathrm{Var~}\mathbf{b}= \begin{pmatrix} \mathrm{Var~}b_0 & \mathrm{Cov}(b_0,b_1) & \cdots & \mathrm{Cov}(b_0,b_k) \\ \mathrm{Cov}(b_1,b_0) & \mathrm{Var~}b_1 & \cdots & \mathrm{Cov}(b_1,b_k) \\ \vdots & \vdots & \ddots & \vdots \\ \mathrm{Cov}(b_k,b_0) & \mathrm{Cov}(b_k,b_1) & \cdots & \mathrm{Var~}b_k \end{pmatrix} = \sigma^2 (\mathbf{X^{\prime}X)}^{-1}. } \tag{3.6} \end{equation}\]

Así, por ejemplo, $\mathrm{Var~}b_j$ es $\sigma^2$ veces la entrada diagonal $(j+1)$ de $(\mathbf{X^{\prime}X)}^{-1}$. Como otro ejemplo, $\mathrm{Cov}(b_0,b_j)$ es $\sigma^2$ veces el elemento en la primera fila y la columna $(j+1)$ de $(\mathbf{X^{\prime}X)}^{-1}$.

Aunque existen métodos alternativos que son preferibles para aplicaciones específicas, los estimadores de mínimos cuadrados han demostrado ser efectivos para muchos análisis de datos rutinarios. Una característica deseable de los estimadores de regresión por mínimos cuadrados se resume en el siguiente resultado bien conocido.

Teorema de Gauss-Markov: Consideremos el modelo de regresión y supongamos que se cumplen las Suposiciones F1-F4. Entonces, dentro de la clase de estimadores que son funciones lineales de las respuestas, el estimador de mínimos cuadrados $\mathbf{b}$ definido en la ecuación (3.4) es el estimador insesgado con la varianza mínima del vector de parámetros $\boldsymbol{\beta}$.

El teorema de Gauss-Markov establece que el estimador de mínimos cuadrados es el más preciso en el sentido de que tiene la menor varianza.

Ya hemos visto en la Propiedad 1 que los estimadores de mínimos cuadrados son insesgados. El teorema de Gauss-Markov afirma que el estimador de mínimos cuadrados es el más preciso en el sentido de que tiene la menor varianza. (En un contexto matricial, “varianza mínima” significa que si $\mathbf{b}^{\ast}$ es cualquier otro estimador, entonces la diferencia de las matrices de varianza, $\mathrm{Var~} \mathbf{b}^{\ast} - \mathrm{Var~}\mathbf{b}$, es semidefinida no negativa.)

Una propiedad adicional importante se refiere a la distribución de los estimadores de regresión por mínimos cuadrados.

Propiedad 3: Consideremos un modelo de regresión y supongamos que se cumplen las Suposiciones F1-F5. Entonces, el estimador de mínimos cuadrados $\mathbf{b}$ definido en la ecuación (3.4) está distribuido normalmente.

Para establecer la Propiedad 3, definimos los vectores de peso, $\mathbf{w}_i = (\mathbf{X^{\prime}X)}^{-1}(1, x_{i1}, \ldots, x_{ik})^{\prime}$. Con esta notación, observamos que

\[ \mathbf{b} = (\mathbf{X^{\prime}X)}^{-1}\mathbf{X}^{\prime}\mathbf{y} = \sum_{i=1}^{n} \mathbf{w}_i y_i, \]

de modo que $\mathbf{b}$ es una combinación lineal de respuestas. Con la Suposición F5, las respuestas están distribuidas normalmente. Debido a que las combinaciones lineales de variables aleatorias normalmente distribuidas también están distribuidas normalmente, tenemos la conclusión de la Propiedad 3. Este resultado sustenta gran parte de la inferencia estadística que se presentará en las Secciones 3.4 y 4.2.

3.3 Estimación y Bondad de Ajuste

Desviación Estándar Residual

Se discutirán propiedades adicionales de los estimadores de los coeficientes de regresión cuando nos enfoquemos en la inferencia estadística. Ahora continuamos nuestra discusión sobre la estimación proporcionando un estimador del otro parámetro en el modelo de regresión lineal, $\sigma^2$.

Nuestro estimador para $\sigma^2$ puede desarrollarse utilizando el principio de reemplazar expectativas teóricas por promedios muestrales. Examinando $\sigma^2 = \mathrm{E}\left( y-\mathrm{E~}y\right)^2$, al reemplazar la expectativa externa por un promedio muestral, se sugiere utilizar el estimador $n^{-1}\sum_{i=1}^{n}(y_i-\mathrm{E~}y_i)^2$. Dado que no observamos $\mathrm{E}~y_i = \beta_0 + \beta_1 x_{i1} + \cdots + \beta_k x_{ik}$, utilizamos en su lugar la cantidad observada correspondiente $b_0 + b_1 x_{i1} + \ldots + b_k x_{ik} = \widehat{y}_i$. Esto conduce a lo siguiente.

Definición. Un estimador de $\sigma^2$, el error cuadrático medio (MSE), se define como

\[\begin{equation} s^2 = \frac{1}{n-(k+1)}\sum_{i=1}^{n}\left( y_i - \widehat{y}_i \right)^2. \tag{3.7} \end{equation}\]

La raíz cuadrada positiva, $s = \sqrt{s^2}$, se llama la desviación estándar residual.

Esta expresión generaliza la definición en la ecuación (2.3), que es válida para $k=1$. Resulta que, al usar $n-(k+1)$ en lugar de $n$ en el denominador de la ecuación (3.7), $s^2$ es un estimador insesgado de $\sigma^2$. Esencialmente, al usar $\widehat{y}_i$ en lugar de $\mathrm{E~}y_i$ en la definición, hemos introducido algunas pequeñas dependencias entre las desviaciones de las respuestas $y_i - \widehat{y}_i$, reduciendo así la variabilidad total. Para compensar esta menor variabilidad, también reducimos el denominador en la definición de $s^2$.

Para proporcionar más intuición sobre la elección de $n-(k+1)$ en la definición de $s^2$, introducimos el concepto de residuales en el contexto de la regresión lineal múltiple. A partir de la Suposición E1, recordemos que los errores aleatorios pueden expresarse como $\varepsilon_i = y_i - (\beta_0 + \beta_1 x_{i1} + \cdots + \beta_k x_{ik})$. Dado que los parámetros $\beta_0, \ldots, \beta_k$ no se observan, los errores en sí mismos no se observan. En su lugar, examinamos los “errores estimados”, o residuales, definidos por $e_i = y_i - \widehat{y}_i$.

A diferencia de los errores, existen ciertas dependencias entre los residuales. Una dependencia se debe al hecho algebraico de que el residual promedio es cero. Además, debe haber al menos $k+2$ observaciones para que haya variación en el ajuste del plano. Si solo tenemos $k+1$ observaciones, podríamos ajustar un plano a los datos perfectamente, resultando en ninguna variación en el ajuste. Por ejemplo, si $k=1$, dado que dos observaciones determinan una línea, se requieren al menos tres observaciones para observar cualquier desviación de la línea. Debido a estas dependencias, solo tenemos $n-(k+1)$ residuales libres, o no restringidos, para estimar la variabilidad en torno al plano de regresión.

La raíz cuadrada positiva de $s^2$ es nuestro estimador de $\sigma$. Usando los residuales, se puede expresar como

\[\begin{equation} s = \sqrt{\frac{1}{n-(k+1)}\sum_{i=1}^{n}e_i^2}. \tag{3.8} \end{equation}\]

Debido a que se basa en residuales, nos referimos a $s$ como la desviación estándar residual. La cantidad $s$ es una medida de nuestro “error típico”. Por esta razón, $s$ también se llama el error estándar de la estimación.

El Coeficiente de Determinación: $R^2$

Para resumir la bondad de ajuste del modelo, como en el Capítulo 2, particionamos la variabilidad en partes que son “explicadas” y “no explicadas” por el ajuste de la regresión. Algebraicamente, los cálculos para la regresión utilizando muchas variables son similares al caso de usar solo una variable. Desafortunadamente, cuando se trata de muchas variables, perdemos la fácil interpretación gráfica como en la Figura 2.4.

Comenzamos con la suma total de desviaciones cuadradas, $Total~SS = \sum_{i=1}^{n}\left( y_i - \overline{y} \right)^2$, como nuestra medida de la variación total en el conjunto de datos. Como en la ecuación (2.1), podemos interpretar la ecuación

\[ \small{ \begin{array}{ccccc} \underbrace{y_i - \overline{y}} & = & \underbrace{y_i - \widehat{y}_i} & + & \underbrace{\widehat{y}_i - \overline{y}} \\ \text{desviación total} & = & \text{desviación no explicada} & + & \text{desviación explicada} \\ \end{array} } \]

como “la desviación sin conocimiento de las variables explicativas es igual a la desviación no explicada por las variables explicativas más la desviación explicada por las variables explicativas”. Al cuadrar cada lado y sumar sobre todas las observaciones se obtiene

\[ Total~SS = Error~SS + Regression~SS \]

donde $Error~SS = \sum_{i=1}^{n}\left( y_i - \widehat{y}_i \right)^2$ y $Regression~SS = \sum_{i=1}^{n}\left( \widehat{y}_i - \overline{y} \right)^2$. Como en la Sección 2.3 para el caso de una variable explicativa, la suma de los términos de producto cruzado resulta ser cero.

Una estadística que resume esta relación es el coeficiente de determinación,

\[ R^2 = \frac{Regression~SS}{Total~SS}. \]

Interpretamos $R^2$ como la proporción de variabilidad explicada por la función de regresión.

Si el modelo es adecuado para los datos, se esperaría una fuerte relación entre las respuestas observadas y las “esperadas” bajo el modelo, los valores ajustados. Un hecho algebraico interesante es el siguiente. Si uno eleva al cuadrado el coeficiente de correlación entre las respuestas y los valores ajustados, obtenemos el coeficiente de determinación, es decir,

\[ R^2 = \left[ r \left(y, \widehat{y} \right) \right]^2. \]

Como resultado, $R$, la raíz cuadrada positiva de $R^2$, se llama el coeficiente de correlación múltiple. Se puede interpretar como la correlación entre la respuesta y la mejor combinación lineal de las variables explicativas, los valores ajustados. (Esta relación se desarrolla utilizando álgebra matricial en el apéndice técnico Sección 5.10.1.)

La descomposición de la variabilidad también se resume utilizando la tabla de análisis de varianza, o ANOVA, como sigue.

\[ \small{ \begin{array}{l|lcl} \hline \text{Fuente} & \text{Suma de Cuadrados} & df & \text{Cuadrado Medio} \\ \hline \text{Regresión} & Regression~SS & k & Regression~MS \\ \text{Error} & Error~SS & n - (k + 1) & MSE \\ \text{Total} & Total~SS & n - 1 & \\ \hline \end{array} } \]

Las cifras de la columna de cuadrados medios se definen como las cifras de suma de cuadrados divididas por sus respectivos grados de libertad. Los grados de libertad del error denotan el número de residuales no restringidos. Es este número el que utilizamos en nuestra definición del “promedio” o error cuadrático medio. Es decir, definimos

\[ MSE = Error~MS = \frac{Error~SS}{n - (k + 1)} = s^2. \]

De manera similar, los grados de libertad de la regresión son el número de variables explicativas. Esto da como resultado

\[ Regression~MS = \frac{Regression~SS}{k}. \]

Al hablar del coeficiente de determinación, se puede establecer que siempre que se añade una variable explicativa al modelo, $R^2$ nunca disminuye. Esto es cierto, independientemente de si la variable adicional es útil o no. Nos gustaría una medida de ajuste que disminuyera cuando se introducen variables inútiles en el modelo como variables explicativas. Para evitar esta anomalía, una estadística ampliamente utilizada es el coeficiente de determinación ajustado por grados de libertad, definido por

\[\begin{equation} R_{a}^2 = 1 - \frac{(Error~SS) / [n - (k + 1)]}{(Total~SS) / (n - 1)} = 1 - \frac{s^2}{s_{y}^2}. \tag{3.9} \end{equation}\]

Para interpretar esta estadística, observe que $s_y^2$ no depende del modelo ni de las variables del modelo. Por lo tanto, $s^2$ y $R_a^2$ son medidas equivalentes de ajuste del modelo. A medida que el ajuste del modelo mejora, $R_{a}^2$ se hace más grande y $s^2$ se hace más pequeño, y viceversa. Dicho de otro modo, elegir un modelo con el menor $s^2$ es equivalente a elegir un modelo con el mayor $R_a^2$.

Ejemplo: Seguro de Vida a Término - Continuación. Para ilustrar, la Tabla 3.3 muestra las estadísticas resumen para la regresión de LNFACE sobre EDUCATION, NUMHH y LNINCOME. A partir de la columna de grados de libertad, recordamos que hay tres variables explicativas y 275 observaciones. Como medidas de ajuste del modelo, el coeficiente de determinación es $R^2 = 34.3\%$ (=$328.47 / 958.90$) y la desviación estándar residual es $s = 1.525$ (=$\sqrt{2.326}$). Si intentáramos estimar el monto nominal logarítmico sin conocimiento de las variables explicativas EDUCATION, NUMHH y LNINCOME, entonces el tamaño del error típico sería $s_y = 1.871$ (=$\sqrt{958.90 / 274}$). Así, al aprovechar nuestro conocimiento de las variables explicativas, hemos podido reducir el tamaño del error típico. La medida de ajuste del modelo que compara estas dos estimaciones de variabilidad es el coeficiente de determinación ajustado, $R_a^2 = 1 - 2.326 / 1.871^2 = 33.6\%$.

Tabla 3.3: **Tabla ANOVA para Seguro de Vida a Término**
	Suma de Cuadrados	$df$	Cuadrado Medio
Regresión	328.47	3	109.49
Error	630.43	271	2.326
Total	958.9	274

Ejemplo: ¿Por qué las Mujeres Viven Más que los Hombres? En un artículo con este título, Lemaire (2002) examinó lo que llamó la “ventaja femenina”, la diferencia en la esperanza de vida entre mujeres y hombres. Las esperanzas de vida son de interés porque se utilizan ampliamente como medidas de la salud de una nación. Lemaire examinó datos de $n = 169$ países y encontró que la ventaja femenina promedio era de 4.51 años en todo el mundo. Buscó explicar esta diferencia basándose en 45 medidas de comportamiento, variables que capturan el grado de modernización económica de una nación, normas sociales/culturales/religiosas, posición geográfica y calidad de la atención médica disponible.

Después de un análisis detallado, Lemaire reporta los coeficientes de un modelo de regresión que aparecen en la Tabla 3.4. Este modelo de regresión explica $R^2 = 61\%$ de la variabilidad. Es un modelo parsimonioso que consiste en solo $k = 4$ de las 45 variables originales.

Tabla 3.4. Coeficientes de Regresión de un Modelo de la Ventaja Femenina

\[ \small{ \begin{array}{l|rr} \hline \text{Variable} & \text{Coeficiente} & t\text{-estadística} \\ \hline \text{Intercepto} & 9.904 & 12.928 \\ \text{Número Logarítmico de Personas por Médico} & -0.473 & -3.212 \\ \text{Fertilidad} & -0.444 & -3.477 \\ \text{Porcentaje de Hindúes y Budistas} & -0.018 & -3.196 \\ \text{Indicador de la Unión Soviética} & 4.922 & 7.235 \\ \hline \end{array} } \]

Fuente: Lemaire (2002)

Todas las variables fueron estadísticamente significativas. El número de personas por médico también estaba correlacionado con otras variables que capturan el grado de modernización económica de un país, como la urbanización, el número de automóviles y el porcentaje de personas que trabajan en la agricultura. La fertilidad, el número de nacimientos por mujer, estaba altamente correlacionada con las variables de educación en el estudio, incluyendo el analfabetismo femenino y la matriculación escolar femenina. El porcentaje de hindúes y budistas es una variable social/cultural/religiosa. El indicador de la Unión Soviética es una variable geográfica: caracteriza a los países de Europa del Este que pertenecían anteriormente a la Unión Soviética. Debido al alto grado de colinealidad entre las 45 variables candidatas, otros analistas podrían fácilmente elegir un conjunto alternativo de variables. No obstante, el punto importante de Lemaire fue que este modelo simple explica aproximadamente el 61% de la variabilidad basada únicamente en variables de comportamiento, no relacionadas con las diferencias biológicas entre sexos.

3.4 Inferencia Estadística para un Coeficiente Único

3.4.1 La Prueba t

En muchas aplicaciones, una sola variable es de interés principal, y otras variables se incluyen en la regresión para controlar fuentes adicionales de variabilidad. Para ilustrar, un agente de ventas podría estar interesado en el efecto que tiene el ingreso sobre la cantidad de seguros demandados. En un análisis de regresión, también se podrían incluir otras variables explicativas como el género de un individuo, tipo de ocupación, edad, tamaño del hogar, nivel educativo, etc. Al incluir estas variables explicativas adicionales, esperamos obtener una mejor comprensión de la relación entre el ingreso y la demanda de seguros. Para llegar a conclusiones sensatas, necesitaremos algunas reglas para decidir si una variable es importante o no.

Respondemos a la pregunta “¿Es $x_j$ importante?” investigando si el parámetro de pendiente correspondiente, $\beta_j$, es igual a cero. La pregunta de si $\beta_j$ es cero se puede replantear en el marco de la prueba de hipótesis como “¿Es válida $H_0:\beta_j=0$?”

Examinamos la proximidad de $b_j$ a cero para determinar si $\beta_j$ es cero o no. Dado que las unidades de $b_j$ dependen de las unidades de $y$ y $x_j$, necesitamos estandarizar esta cantidad. A partir de la Propiedad 2 y la ecuación (3.6), vimos que $\mathrm{Var~}b_j$ es $\sigma^2$ multiplicado por el elemento diagonal $(j+1)^{st}$ de $(\mathbf{X^{\prime}X})^{-1}$. Reemplazando $\sigma^2$ por el estimador $s^2$ y tomando raíces cuadradas, tenemos lo siguiente.

Definición. El error estándar de $b_j$ se puede expresar como

\[ se(b_j) = s \sqrt{\text{elemento diagonal (j+1)st de } (\mathbf{X^{\prime}X})^{-1}}. \]

Recuerda que un error estándar es una desviación estándar estimada. Para probar $H_0:\beta_j=0$, examinamos la razón $t$, $t(b_j) = \frac{b_j}{se(b_j)}$. Interpretamos $t(b_j)$ como el número de errores estándar que $b_j$ está alejado de cero. Esta es la cantidad adecuada porque se puede demostrar que la distribución de muestreo de $t(b_j)$ es la distribución $t$ con $df=n-(k+1)$ grados de libertad, bajo la hipótesis nula y con los supuestos del modelo de regresión lineal F1-F5. Esto nos permite construir pruebas de la hipótesis nula como el siguiente procedimiento:

Procedimiento. La Prueba t para un Coeficiente de Regresión ($\beta$).

La hipótesis nula es $H_0:\beta_j=0$.
La hipótesis alternativa es $H_{a}:\beta_j \neq 0$.
Establecer un nivel de significancia $\alpha$ (típicamente, pero no necesariamente, 5%).
Construir la estadística, $t(b_j) = \frac{b_j}{se(b_j)}$.
Procedimiento: Rechazar la hipótesis nula a favor de la alternativa si $|t(b_j)|$ excede un valor $t$. Aquí, este valor $t$ es el percentil $(1-\alpha /2)^{th}$ de la distribución $t$ con $df=n-(k+1)$ grados de libertad, denotado como $t_{n-(k+1),1-\alpha /2}$.

En muchas aplicaciones, el tamaño de la muestra será lo suficientemente grande como para que podamos aproximar el valor $t$ por el percentil correspondiente de la curva normal estándar. Al nivel de significancia del 5%, este percentil es 1.96. Así, como regla general, podemos interpretar que una variable es importante si su razón $t$ excede dos en valor absoluto.

Aunque es la más común, probar $H_0:\beta_j=0$ frente a $H_{a}:\beta_j \neq 0$ es solo una de las muchas pruebas de hipótesis que se pueden realizar. Tabla 3.5 describe procedimientos alternativos para la toma de decisiones. Estos procedimientos son para probar $H_0:\beta_j = d$. Aquí, $d$ es un valor prescrito por el usuario que puede ser igual a cero o cualquier otro valor conocido.

Tabla 3.5. Procedimientos de Toma de Decisiones para Probar $H_0: \beta_j = d$

\[ \small{ \begin{array}{cc} \hline \text{Hipótesis Alternativa }(H_{a}) & \text{Procedimiento: Rechazar } H_0 \text{ en favor de } H_a \text{ si }\\ \hline \beta_j > d & t-\mathrm{razón}>t_{n-(k+1),1-\alpha } \\ \beta_j < d & t-\mathrm{razón}<-t_{n-(k+1),1-\alpha } \\ \beta_j\neq d & |t-\mathrm{razón}\mathit{|}>t_{n-(k+1),1-\alpha/2} \end{array} \\ \begin{array}{ll}\hline \textit{Notas:} &\text{ El nivel de significancia es } \alpha. \text{ Aquí, } t_{n-(k+1),1-\alpha}\text{ es el }(1-\alpha)^{th}\text{ percentil} \\ &~~\text{de la distribución }t-\text{utilizando } df=n-(k+1)\text{ grados de libertad.} \\ &~~\text{La estadística de prueba es }t-\mathrm{razón} = (b_j -d)/se(b_j) . \\ \hline \end{array} } \]

Alternativamente, se pueden construir valores $p$ y compararlos con niveles de significancia dados. El valor $p$ permite al lector del informe entender la fuerza de la desviación de la hipótesis nula. Tabla 3.6 resume el procedimiento para calcular los valores $p$.

Tabla 3.6. Valores de Probabilidad para Probar $H_0:\beta_j =d$

\[ \small{ \begin{array}{cccc} \hline \text{Hipótesis} & & & \\ \text{Alternativa} (H_a ) & \beta_j > d & \beta_j < d & \beta_j \neq d \\ \hline p-valor & \Pr(t_{n-(k+1)}>t-ratio) & \Pr(t_{n-(k+1)}<t-ratio) & \Pr(|t_{n-(k+1)}|>|t-ratio|) \\ \end{array} \\ \begin{array}{ll}\hline \textit{Notas:} & \text{ Aquí, } t_{n-(k+1)} \text{ es una variable aleatoria con distribución }t\text{ con }df=n-(k+1)\text{ grados de libertad.} \\ &~~\text{La estadística de prueba es }t-\mathrm{ratio} = (b_j -d)/se(b_j) . \\ \hline \end{array} } \]

Ejemplo: Seguro de Vida Temporal - Continuación. Una convención útil al reportar los resultados de un análisis estadístico es colocar el error estándar de una estadística entre paréntesis debajo de esa estadística. Así, por ejemplo, en nuestra regresión de LNFACE sobre EDUCATION, NUMHH, y LNINCOME, la ecuación de regresión estimada es:

\[ \begin{array}{lccccc} \widehat{LNFACE} = &2.584 ~ + &0.206~ \text{EDUCATION} + &0.306 ~\text{NUMHH} + &0.494 ~\text{LNINCOME}. \\ \text{error estándar} &(0.846) &(0.039) &(0.063) &(0.078). \end{array} \]

Para ilustrar el cálculo de los errores estándar, primero notemos que, según la Tabla 3.3, tenemos que la desviación estándar residual es $s=1.525$. Usando un paquete estadístico, tenemos

\[ \small{ (\mathbf{X^{\prime}X})^{-1} = \begin{pmatrix} 0.307975 & -0.004633 & -0.002131 & -0.020697 \\ -0.004633 & 0.000648 & 0.000143 & -0.000467 \\ -0.002131 & 0.000143 & 0.001724 & -0.000453 \\ -0.020697 & -0.000467 & -0.000453 & 0.002585 \end{pmatrix}. } \]

Para ilustrar, podemos calcular $se(b_3)=s \times \sqrt{0.002585} = 0.078$, como se indicó antes. El cálculo de los errores estándar, así como las correspondientes estadísticas $t$, es parte del resultado estándar de los programas estadísticos y no necesita ser realizado por los usuarios. Nuestro objetivo aquí es ilustrar las ideas subyacentes a los cálculos rutinarios.

Con esta información, podemos calcular inmediatamente las razones $t$ para verificar si un coeficiente asociado con una variable individual es significativamente diferente de cero. Por ejemplo, la razón $t$ para la variable LNINCOME es $t(b_3) = \frac{0.494}{0.078} = 6.3$. La interpretación es que $b_3$ está más de cuatro errores estándar por encima de cero, y por lo tanto LNINCOME es una variable importante en el modelo. Más formalmente, podemos estar interesados en probar la hipótesis nula de que $H_0:\beta_3 = 0$ frente a $H_0:\beta_3 \neq 0$. A un nivel de significancia del 5%, el valor $t$ es 1.96, porque $df=275-(1+3)=271$. Por lo tanto, rechazamos la hipótesis nula en favor de la hipótesis alternativa, que el ingreso logarítmico (LNINCOME) es importante para determinar el monto logarítmico del seguro.

3.4.2 Intervalos de Confianza

Los intervalos de confianza para los parámetros son otra forma de describir la fuerza de la contribución de la $j$-ésima variable explicativa. La estadística $b_j$ se llama una estimación puntual del parámetro $\beta_j$. Para proporcionar un rango de confianza, usamos el intervalo de confianza:

\[\begin{equation} b_j \pm t_{n-(k+1),1-\alpha /2}~se(b_j). \tag{3.10} \end{equation}\]

Aquí, el valor $t$ $t_{n-(k+1),1-\alpha /2}$ es un percentil de la distribución $t$ con $df=n-(k+1)$ grados de libertad. Usamos el mismo valor $t$ que en la prueba de hipótesis bilateral. De hecho, hay una dualidad entre el intervalo de confianza y la prueba de hipótesis bilateral. Por ejemplo, no es difícil comprobar que si un valor hipotético cae fuera del intervalo de confianza, entonces $H_0$ será rechazado en favor de $H_{a}$. Además, el conocimiento del $p$-valor, la estimación puntual y el error estándar se puede utilizar para determinar un intervalo de confianza.

3.4.3 Gráficos de Variables Añadidas

Para representar datos multivariados de forma gráfica, hemos visto que una matriz de dispersión es una herramienta útil. Sin embargo, la principal limitación de la matriz de dispersión es que solo captura relaciones entre pares de variables. Cuando los datos se pueden resumir utilizando un modelo de regresión, una herramienta gráfica que no tiene esta limitación es el gráfico de variables añadidas. El gráfico de variables añadidas también se llama gráfico de regresión parcial porque, como veremos, se construye en términos de los residuos de ciertos ajustes de regresión. También veremos que el gráfico de variables añadidas se puede resumir en términos de un coeficiente de correlación parcial, proporcionando así un vínculo entre correlación y regresión. Para introducir estas ideas, trabajamos en el contexto del siguiente ejemplo.

Ejemplo: Precios de Refrigeradores. ¿Qué características de un refrigerador son importantes para determinar su precio (PRICE)? Aquí consideramos varias características de un refrigerador, incluyendo el tamaño del refrigerador en pies cúbicos (RSIZE), el tamaño del compartimento del congelador en pies cúbicos (FSIZE), la cantidad promedio de dinero gastado por año para operar el refrigerador (ECOST, por “costo de energía”), el número de estantes en las puertas del refrigerador y del congelador (SHELVES), y el número de características (FEATURES). La variable de características incluye estantes para latas, cajones transparentes, fabricantes de hielo, portahuevos, y así sucesivamente.

Tanto los consumidores como los fabricantes están interesados en modelos de precios de refrigeradores. Otras cosas iguales, los consumidores generalmente prefieren refrigeradores más grandes con menores costos de energía y que tengan más características. Debido a las fuerzas de la oferta y la demanda, esperaríamos que los consumidores paguen más por estos refrigeradores. Un refrigerador más grande con menores costos de energía y que tiene más características a un precio similar se considera una ganga para el consumidor. ¿Cuánto estaría dispuesto a pagar el consumidor por este espacio adicional? Un modelo de precios para refrigeradores en el mercado proporciona algo de información sobre esta cuestión.

Para este fin, analizamos datos de $n=37$ refrigeradores. La Tabla 3.7 proporciona las estadísticas descriptivas básicas para la variable de respuesta PRICE y las cinco variables explicativas. De esta tabla, vemos que el precio promedio de los refrigeradores es $\overline{y} = \$626.40$, con una desviación estándar de $s_{y} = \$139.80$. De manera similar, la cantidad promedio anual para operar un refrigerador, o ECOST promedio, es $70.51.

Tabla 3.4: Silly. Create a table just to update the counter…
x
2

Tabla 3.5: Silly.
x
2

Tabla 3.6: Silly.
x
2

Tabla 3.7: **Estadísticas Descriptivas para cada variable para 37 Refrigeradores**
	Media	Mediana	Desviación Estándar	Mínimo	Máximo
ECOST	70.514	68.0	9.140	60.0	94.0
RSIZE	13.400	13.2	0.600	12.6	14.7
FSIZE	5.184	5.1	0.938	4.1	7.4
SHELVES	2.514	2.0	1.121	1.0	5.0
FEATURES	3.459	3.0	2.512	1.0	12.0
PRICE	626.351	590.0	139.790	460.0	1200.0

Para analizar las relaciones entre pares de variables, la Tabla 3.8 proporciona una matriz de coeficientes de correlación. En la tabla, vemos que hay relaciones lineales fuertes entre PRICE y tanto el espacio del congelador (FSIZE) como el número de FEATURES. Sorprendentemente, también hay una fuerte correlación positiva entre PRICE y ECOST. Recordemos que ECOST es el costo de energía; uno podría esperar que los refrigeradores de mayor precio deberían tener menores costos de energía.

Tabla 3.8: **Matriz de Coeficientes de Correlación**
	ECOST	RSIZE	FSIZE	SHELVES	FEATURES
RSIZE	-0.033
FSIZE	0.855	-0.235
SHELVES	0.188	-0.363	0.251
FEATURES	0.334	-0.096	0.439	0.16
PRICE	0.522	-0.024	0.72	0.4	0.697

R Code to Produce Tables 3.7 and 3.8

Se ajustó un modelo de regresión a los datos. La ecuación de regresión ajustada aparece en la Tabla 3.9, con $s=60.65$ y $R^2=83.8\%$.

Tabla 3.9: **Modelo Ajustado de Precio de Refrigeradores**
	Coeficiente	Desviación Estándar	$t$-Ratio
Intercepto	798.00	271.400	-2.9
ECOST	-6.96	2.275	-3.1
RSIZE	76.50	19.440	3.9
FSIZE	137.00	23.760	5.8
SHELVES	37.90	9.886	3.8
FEATURES	23.80	4.512	5.3

De la Tabla 3.9, las variables explicativas parecen ser buenos predictores de los precios de los refrigeradores. Juntas, estas variables explican el 83.8% de la variabilidad. Para entender los precios, el error típico ha disminuido de $s_{y} = \$139.80$ a $s = \$60.65$. Los $t$-ratios para cada una de las variables explicativas superan el valor absoluto de dos, lo que indica que cada variable es importante de manera individual.

Lo que sorprende del ajuste de la regresión es el coeficiente negativo asociado con el costo de energía. Recordemos que podemos interpretar $b_{ECOST} = -6.96$ como que, por cada aumento de un dólar en ECOST, esperamos que el PRICE disminuya en $6.96. Esta relación negativa está conforme con nuestra intuición económica. Sin embargo, es sorprendente que el mismo conjunto de datos nos haya mostrado que existe una relación positiva entre PRICE y ECOST. Esta aparente anomalía se debe a que la correlación solo mide las relaciones entre pares de variables, mientras que el ajuste de la regresión puede considerar varias variables simultáneamente. Para proporcionar más información sobre esta aparente anomalía, ahora introducimos el gráfico de variables añadidas.

Producción de un Gráfico de Variables Añadidas

El gráfico de variables añadidas proporciona vínculos adicionales entre la metodología de regresión y herramientas más fundamentales como los diagramas de dispersión y las correlaciones. Trabajamos en el contexto del Ejemplo del Precio de los Refrigeradores para demostrar la construcción de este gráfico.

Procedimiento para producir un gráfico de variables añadidas.

Realiza una regresión de PRICE sobre RSIZE, FSIZE, SHELVES y FEATURES, omitiendo ECOST. Calcula los residuos de esta regresión, los cuales etiquetamos como $e_1$.
Realiza una regresión de ECOST sobre RSIZE, FSIZE, SHELVES y FEATURES. Calcula los residuos de esta regresión, los cuales etiquetamos como $e_2$.
Grafica $e_1$ versus $e_2$. Este es el gráfico de variables añadidas de PRICE versus ECOST, controlando por los efectos de RSIZE, FSIZE, SHELVES y FEATURES. Este gráfico aparece en la Figura 3.4.

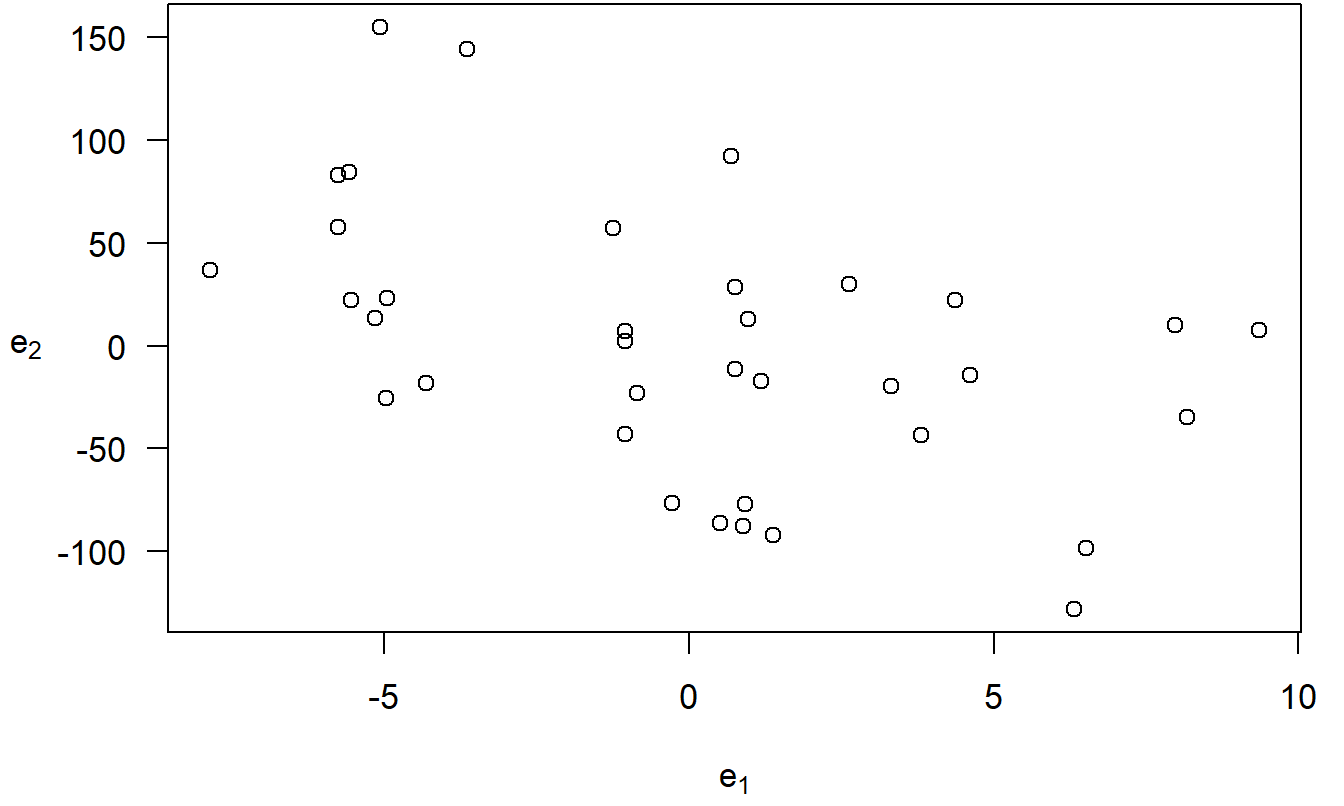
Un gráfico de variables añadidas. Los residuos de la regresión de PRICE sobre las variables explicativas, omitiendo ECOST, están en el eje horizontal. En el eje vertical están los residuos de la regresión de ECOST sobre las demás variables explicativas. El coeficiente de correlación es -0.48.

Figura 3.4: Un gráfico de variables añadidas. Los residuos de la regresión de PRICE sobre las variables explicativas, omitiendo ECOST, están en el eje horizontal. En el eje vertical están los residuos de la regresión de ECOST sobre las demás variables explicativas. El coeficiente de correlación es -0.48.

Código en R para producir la Figura 3.4

El error $\varepsilon$ puede interpretarse como la variación natural en una muestra. En muchas situaciones, esta variación natural es pequeña en comparación con los patrones evidentes en el componente de regresión no aleatorio. Por lo tanto, es útil pensar en el error, $\varepsilon_i = y_i - \left( \beta_0 + \beta_1 x_{i1} + \ldots + \beta_k x_{ik} \right)$, como la respuesta después de controlar por los efectos de las variables explicativas. En la Sección 3.3, vimos que un error aleatorio puede aproximarse mediante un residuo, $e_i = y_i - \left( b_0 + b_1 x_{i1} + \cdots + b_k x_{ik} \right)$. De la misma manera, podemos pensar en un residuo como la respuesta después de “controlar” los efectos de las variables explicativas.

Con esto en mente, podemos interpretar el eje vertical de la Figura 3.4 como el precio del refrigerador (PRICE) controlado por los efectos de RSIZE, FSIZE, SHELVES y FEATURES. De manera similar, podemos interpretar el eje horizontal como ECOST controlado por los efectos de RSIZE, FSIZE, SHELVES y FEATURES. El gráfico proporciona entonces una representación gráfica de la relación entre PRICE y ECOST, después de controlar por las demás variables explicativas. En comparación, un diagrama de dispersión de PRICE y ECOST (no mostrado aquí) no controla por las demás variables explicativas. Por lo tanto, es posible que la relación positiva entre PRICE y ECOST no se deba a una relación causal, sino más bien a una o más variables adicionales que hacen que ambas variables sean grandes.

Por ejemplo, de la Tabla 3.8, vemos que el tamaño del congelador (FSIZE) está positivamente correlacionado tanto con ECOST como con PRICE. Ciertamente parece razonable que aumentar el tamaño de un congelador cause que tanto el costo de energía como el precio aumenten. Más bien, la correlación positiva puede deberse al hecho de que valores grandes de FSIZE significan valores grandes tanto de ECOST como de PRICE.

Las variables omitidas en una regresión se llaman variables omitidas. Esta omisión podría causar un problema serio en el ajuste del modelo de regresión; los coeficientes de regresión podrían no solo ser significativamente fuertes cuando no deberían serlo, sino que también podrían tener el signo incorrecto. Seleccionar el conjunto adecuado de variables para incluir en el modelo de regresión es una tarea importante; es el tema de los Capítulos 5 y 6.

3.4.4 Coeficientes de Correlación Parcial

Como vimos en el Capítulo 2, una estadística de correlación es una cantidad útil para resumir gráficos. La correlación en el gráfico de variables añadidas se llama coeficiente de correlación parcial. Se define como la correlación entre los residuos $e_1$ y $e_2$ y se denota por $r(y,x_j | x_1, \ldots, x_{j-1}, x_{j+1}, \ldots, x_k)$. Debido a que resume un gráfico de variables añadidas, podemos interpretar $r(y,x_j | x_1, \ldots, x_{j-1}, x_{j+1}, \ldots, x_k)$ como la correlación entre $y$ y $x_j$, en presencia de las otras variables explicativas. Por ejemplo, la correlación entre PRICE y ECOST en presencia de las otras variables explicativas es -0.48.

El coeficiente de correlación parcial también se puede calcular utilizando

\[\begin{equation} r(y,x_j | x_1, \ldots, x_{j-1}, x_{j+1}, \ldots, x_k) = \frac{t(b_j)}{\sqrt{t(b_j)^2 + n - (k + 1)}}. \tag{3.11} \end{equation}\]

Aquí, $t(b_j)$ es el $t$-ratio para $b_j$ de una regresión de $y$ sobre $x_1, \ldots, x_k$ (incluyendo la variable $x_j$). Un aspecto importante de esta ecuación es que nos permite calcular coeficientes de correlación parcial ejecutando solo una regresión. Por ejemplo, en la Tabla 3.9, la correlación parcial entre PRICE y ECOST en presencia de las otras variables explicativas es $\frac{-3.1}{\sqrt{(-3.1)^2 + 37 - (5 + 1)}} \approx -0.48$.

El cálculo de coeficientes de correlación parcial es más rápido cuando se usa la relación con el $t$-ratio, pero puede fallar en detectar relaciones no lineales. La información en la Tabla 3.9 nos permite calcular los cinco coeficientes de correlación parcial en el Ejemplo del Precio de los Refrigeradores después de ejecutar solo una regresión. El procedimiento de tres pasos para producir gráficos de variables añadidas requiere diez regresiones, dos para cada una de las cinco variables explicativas. Por supuesto, al producir gráficos de variables añadidas, podemos detectar relaciones no lineales que son omitidas por los coeficientes de correlación.

Los coeficientes de correlación parcial proporcionan otra interpretación para los $t$-ratios. La ecuación muestra cómo calcular una estadística de correlación a partir de un $t$-ratio, proporcionando así otro vínculo entre la correlación y el análisis de regresión. Además, de la ecuación vemos que cuanto mayor es el $t$-ratio, mayor es el coeficiente de correlación parcial. Es decir, un $t$-ratio alto significa que existe una gran correlación entre la respuesta y la variable explicativa, controlando por las otras variables explicativas. Esto proporciona una respuesta parcial a la pregunta que suelen hacer los consumidores de análisis de regresión: “¿Cuál es la variable más importante?”

3.5 Algunas Variables Explicativas Especiales

El modelo de regresión lineal es la base de una rica familia de modelos. Esta sección ofrece varios ejemplos para ilustrar la riqueza de esta familia. Estos ejemplos demuestran el uso de (i) variables binarias, (ii) transformación de variables explicativas y (iii) términos de interacción. Esta sección también sirve para subrayar el significado del adjetivo lineal en la frase “regresión lineal”; la función de regresión es lineal en los parámetros pero puede ser una función altamente no lineal de las variables explicativas.

3.5.1 Variables Binarias

Las variables categóricas proporcionan una etiqueta numérica para mediciones de observaciones que caen en grupos distintos, o categorías. Debido a la agrupación, las variables categóricas son discretas y generalmente toman un número finito de valores. Comenzamos nuestra discusión con una variable categórica que puede tomar uno de solo dos valores, una variable binaria. Una discusión más detallada sobre las variables categóricas es el tema del Capítulo 4.

Ejemplo: Seguro de Vida a Término - Continuación. Ahora consideramos el estado civil del encuestado. En la Encuesta de Finanzas del Consumidor, los encuestados pueden seleccionar entre varias opciones que describen su estado civil, incluyendo “casado”, “viviendo con una pareja”, “divorciado”, y así sucesivamente. El estado civil no se mide de manera continua, sino que toma valores que caen en grupos distintos. En este capítulo, agrupamos a los encuestados de acuerdo a si están solteros o no, definidos para incluir a aquellos que están separados, divorciados, viudos, nunca casados, y que no están casados ni viviendo con una pareja. El Capítulo 4 presentará un análisis más completo del estado civil incluyendo categorías adicionales.

La variable binaria SINGLE se define como uno si el encuestado está soltero y 0 en caso contrario. La variable SINGLE también se conoce como una variable indicadora porque indica si el encuestado está soltero o no. Otro nombre para este tipo importante de variable es una variable dummy. Podríamos usar 0 y 100, o 20 y 36, o cualquier otro par de valores distintos. Sin embargo, 0 y 1 son convenientes para la interpretación de los valores de los parámetros, discutidos a continuación. Para simplificar la discusión, presentamos ahora un modelo utilizando solo LNINCOME y SINGLE como variables explicativas.

Para nuestra muestra de $n = 275$ hogares, 57 son solteros y los otros 218 no lo son. Para ver las relaciones entre LNFACE, LNINCOME y SINGLE, la Figura 3.5 introduce un gráfico de letras de LNFACE versus LNINCOME, con SINGLE como la variable de código. Podemos ver que la Figura 3.5 es un diagrama de dispersión de LNFACE versus LNINCOME, usando 50 hogares seleccionados aleatoriamente de nuestra muestra de 275 (para mayor claridad del gráfico). Sin embargo, en lugar de usar el mismo símbolo de gráfico para cada observación, hemos codificado los símbolos para que podamos entender fácilmente el comportamiento de una tercera variable, SINGLE. En otras aplicaciones, puede optar por usar otros símbolos de gráfico como $\clubsuit$, $\heartsuit$, $\spadesuit$, y así sucesivamente, o usar diferentes colores, para codificar información adicional. Para esta aplicación, se seleccionaron los códigos de letras “S” para solteros y “o” para otros porque recuerdan al lector la naturaleza del esquema de codificación. Independientemente del esquema de codificación, el punto importante es que un gráfico de letras es un dispositivo útil para representar gráficamente tres o más variables en dos dimensiones. La principal restricción es que la información adicional debe estar categorizada, como con las variables binarias, para que el esquema de codificación funcione.

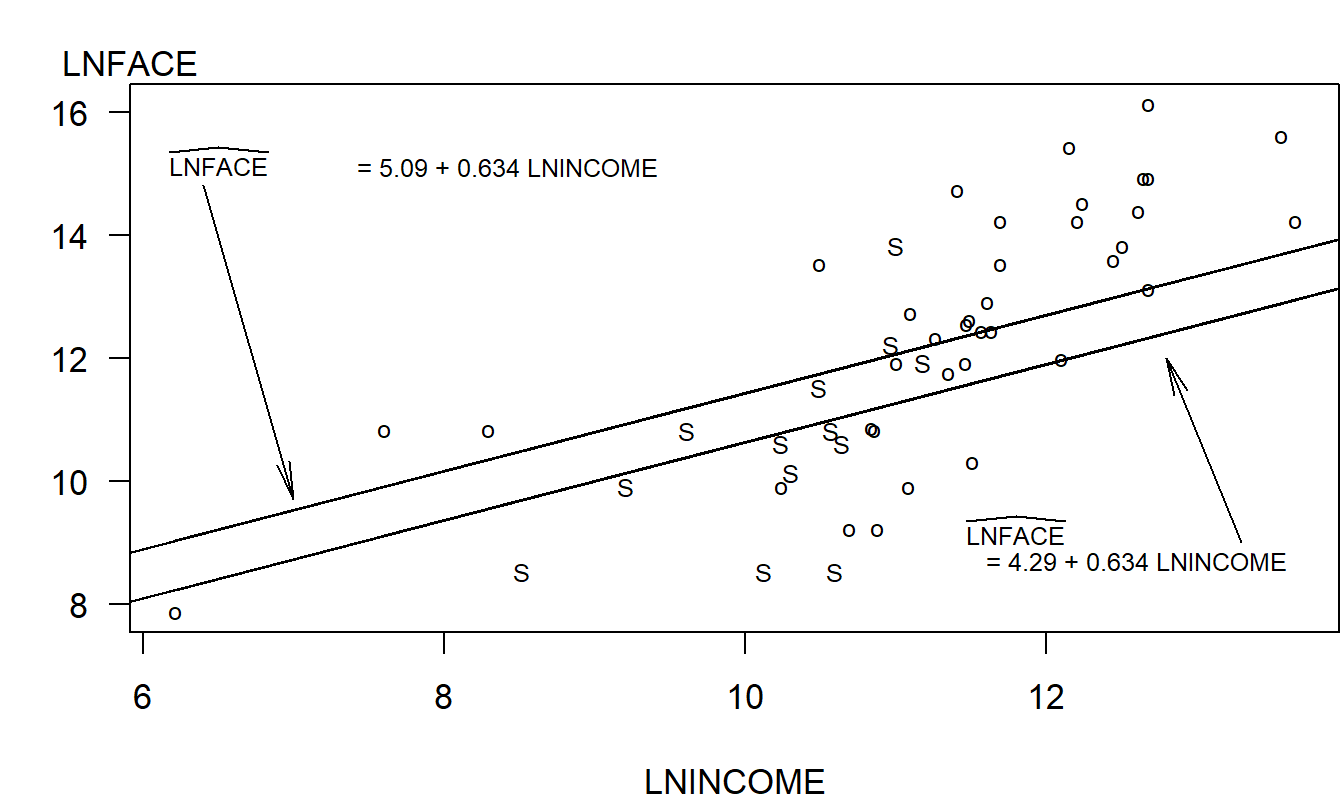
Gráfico de letras de LNFACE versus LNINCOME, con el código de letra ‘S’ para solteros y ‘o’ para otros. Las líneas de regresión ajustadas han sido superpuestas. La línea inferior es para solteros y la línea superior es para otros.

Figura 3.5: Gráfico de letras de LNFACE versus LNINCOME, con el código de letra ‘S’ para solteros y ‘o’ para otros. Las líneas de regresión ajustadas han sido superpuestas. La línea inferior es para solteros y la línea superior es para otros.

La Figura 3.5 sugiere que LNFACE es más bajo para aquellos solteros que para otros para un nivel dado de ingreso. Por lo tanto, ahora consideramos un modelo de regresión, LNFACE = β_0 + β_1 LNINCOME + β_2 SINGLE + ϵ. La función de regresión se puede escribir como:

\[ \text{E } y = \begin{cases} \beta_0 + \beta_1 \text{LNINCOME} & \text{para otros encuestados} \\ \beta_0 + \beta_2 + \beta_1 \text{LNINCOME} & \text{para encuestados solteros} \end{cases} \]

La interpretación de los coeficientes del modelo difiere del caso de variables continuas. Para variables continuas como LNINCOME, interpretamos $\beta_1$ como el cambio esperado en $y$ por unidad de cambio en el ingreso logarítmico, manteniendo fijas otras variables. Para variables binarias como SINGLE, interpretamos $\beta_2$ como el aumento esperado en $y$ al pasar del nivel base de SINGLE (=0) al nivel alternativo. Así, aunque tenemos un modelo para ambos estados civiles, podemos interpretar el modelo usando dos ecuaciones de regresión, una para cada tipo de estado civil. Al escribir una ecuación separada para cada estado civil, hemos simplificado una complicada ecuación de regresión múltiple. A veces, es más fácil comunicar una serie de relaciones simples en comparación con una sola relación compleja.

Aunque la interpretación para variables explicativas binarias difiere de la continua, el método de estimación de mínimos cuadrados ordinarios sigue siendo válido. Para ilustrar, la versión ajustada del modelo anterior es

\[ \small{ \begin{array}{cclll} \widehat{LNFACE} & = & 5.09 & + 0.634 \text{LNINCOME} & - 0.800 \text{SINGLE} .\\ \text{error estándar} & & (0.89) & ~~(0.078) & ~(0.248) \\ \end{array} } \]

Para interpretar $b_2 = -0.800$, decimos que esperamos que el logaritmo de la cara sea menor en 0.80 para un encuestado que es soltero en comparación con la otra categoría. Esto asume que otras cosas, como el ingreso, permanecen constantes. Para una interpretación gráfica, las dos líneas de regresión ajustadas están superpuestas en la Figura 3.5.

3.5.2 Transformación de Variables Explicativas

Los modelos de regresión tienen la capacidad de representar relaciones complejas y no lineales entre la respuesta esperada y las variables explicativas. Por ejemplo, los textos tempranos sobre regresión, como Plackett (1960, Capítulo 6), dedican un capítulo completo al modelo de regresión polinómica,

\[\begin{equation} \text{E } y = \beta_0 + \beta_1 x + \beta_2 x^2 + \ldots + \beta_p x^p. \tag{3.12} \end{equation}\]

Aquí, la idea es que un polinomio de orden $p$ en $x$ puede usarse para aproximar funciones generales y desconocidas no lineales de $x$.

El tratamiento moderno de la regresión polinómica no requiere un capítulo completo porque el modelo en la ecuación (3.12) puede expresarse como un caso especial del modelo de regresión lineal. Es decir, con la función de regresión en la ecuación (3.5), $\text{E } y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_k x_k$, podemos elegir $k = p$ y $x_1 =x$, $x_2 = x^2$, $\ldots$, $x_p = x^p$. Así, con estas elecciones de variables explicativas, podemos modelar una función altamente no lineal de $x$.

No estamos restringidos a potencias de $x$ en nuestra elección de transformaciones. Por ejemplo, el modelo $\text{E } y = \beta_0 + \beta_1 \ln x$, proporciona otra forma de representar una curva suavemente inclinada en $x$. Este modelo puede escribirse como un caso especial del modelo de regresión lineal básico usando $x^{\ast} = \ln x$ como la versión transformada de $x$.

Las transformaciones de las variables explicativas no tienen que ser funciones suaves. Para ilustrar, en algunas aplicaciones, es útil categorizar una variable explicativa continua. Por ejemplo, supongamos que $x$ representa el número de años de educación, que varía de 0 a 17. Si nos basamos en información auto-reportada por nuestra muestra de personas mayores, puede haber una cantidad considerable de error en la medición de $x$. Podríamos optar por usar una transformación menos informativa, pero más confiable, de $x$ como $x^{\ast}$, una variable binaria para haber completado 13 años de escolaridad (terminar la secundaria). Formalmente, codificaríamos $x^{} = 1$ si $x \geq 13$ y $x^{\ast} = 0$ si $x < 13$.

Así, hay varias formas en que las funciones no lineales de las variables explicativas pueden usarse en el modelo de regresión. Un ejemplo de un modelo de regresión no lineal es $y = \beta_0 + \exp (\beta_1 x) + \varepsilon.$ Estos típicamente surgen en aplicaciones científicas de regresiones donde hay principios científicos fundamentales que guían el desarrollo del modelo complejo.

3.5.3 Términos de Interacción

Hasta ahora hemos discutido cómo las variables explicativas, digamos $x_1$ y $x_2$, afectan la respuesta media de manera aditiva, es decir, $\mathrm{E}~y = \beta_0 + \beta_1 x_1 + \beta_2 x_2$. Aquí, esperamos que $y$ aumente en $\beta_1$ por cada unidad que aumente $x_1$, manteniendo $x_2$ fijo. ¿Qué pasa si la tasa marginal de aumento de $\mathrm{E}~y$ difiere para valores altos de $x_2$ en comparación con valores bajos de $x_2$? Una forma de representar esto es crear una variable de interacción $x_3 = x_1 \times x_2$ y considerar el modelo $\mathrm{E}~y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3$.

Con este modelo, el cambio en el esperado $y$ por cada unidad de cambio en $x_1$ ahora depende de $x_2$. Formalmente, podemos evaluar pequeños cambios en la función de regresión como:

\[ \frac{\partial \mathrm{E}~y}{\partial x_1} = \frac{\partial}{\partial x_1} \left(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_1 x_2 \right) = \beta_1 + \beta_3 x_2 . \]

De esta manera, podemos permitir funciones más complicadas de $x_1$ y $x_2$. La Figura 3.6 ilustra esta estructura compleja. A partir de esta figura y los cálculos anteriores, vemos que los cambios parciales de $\mathrm{E}~y$ debido al movimiento de $x_1$ dependen del valor de $x_2$. De esta manera, decimos que los cambios parciales debidos a cada variable no son independientes, sino que “se mueven juntos.”

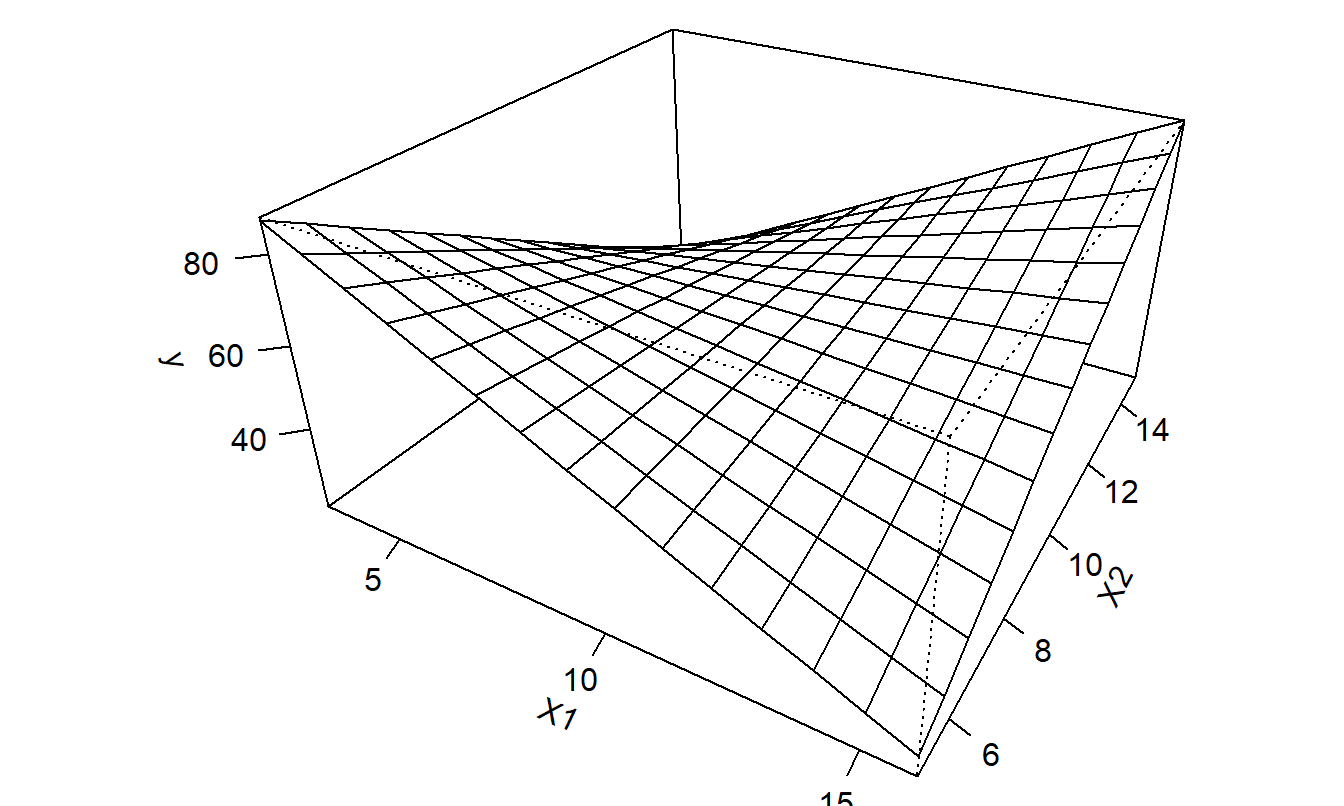
$Gráfico de $\mathrm{E}~y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_1 x_2$ versus $x_1$ y $x_2$.$

Figura 3.6: Gráfico de $\mathrm{E}~y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_1 x_2$ versus $x_1$ y $x_2$.

De manera más general, un término de interacción es una variable que se crea como una función no lineal de dos o más variables explicativas. Estos términos especiales, aunque nos permiten explorar una familia rica de funciones no lineales, pueden considerarse casos especiales del modelo de regresión lineal. Para hacer esto, simplemente creamos la variable de interés y tratamos este nuevo término como otra variable explicativa. Por supuesto, no todas las variables que creamos serán útiles. En algunos casos, la variable creada será tan similar a las variables ya presentes en nuestro modelo que no nos proporcionará nueva información. Afortunadamente, podemos usar pruebas $t$ para verificar si la nueva variable es útil. Además, el Capítulo 4 presentará una prueba para decidir si un grupo de variables es útil.

La función que usamos para crear una variable de interacción debe ser más que una combinación lineal de otras variables explicativas. Por ejemplo, si usamos $x_3 = x_1 + x_2$, no podremos estimar todos los parámetros. El Capítulo 5 presentará algunas técnicas para ayudar a evitar situaciones en las que una variable es una combinación lineal de las demás.

Para darles una idea de la amplia variedad de aplicaciones potenciales de variables explicativas especiales, ahora presentamos una serie de ejemplos breves.

Ejemplo: Seguro de Vida a Término - Continuación. ¿Cómo interpretamos la interacción de una variable binaria con una variable continua? Para ilustrar, consideremos un modelo de regresión para Seguro de Vida a Término,

\[ \mathrm{LNFACE} = \beta_0 + \beta_1 \mathrm{LNINCOME} + \beta_2 \mathrm{SINGLE} + \beta_3 \mathrm{LNINCOME*SINGLE} + \varepsilon . \]

En este modelo, hemos creado una tercera variable explicativa a través de la interacción de LNINCOME y SINGLE. La función de regresión se puede escribir como:

\[ \mathrm{E}~y = \begin{cases} \beta_0 + \beta_1 \mathrm{LNINCOME}, & \text{para otros encuestados}, \\ \beta_0 + \beta_2 + (\beta_1 + \beta_3) \mathrm{LNINCOME}, & \text{para encuestados solteros}. \end{cases} \]

Así, a través de este único modelo con cuatro parámetros, podemos crear dos líneas de regresión separadas, una para los solteros y otra para los demás. La Figura 3.7 muestra las dos líneas de regresión ajustadas para nuestros datos.

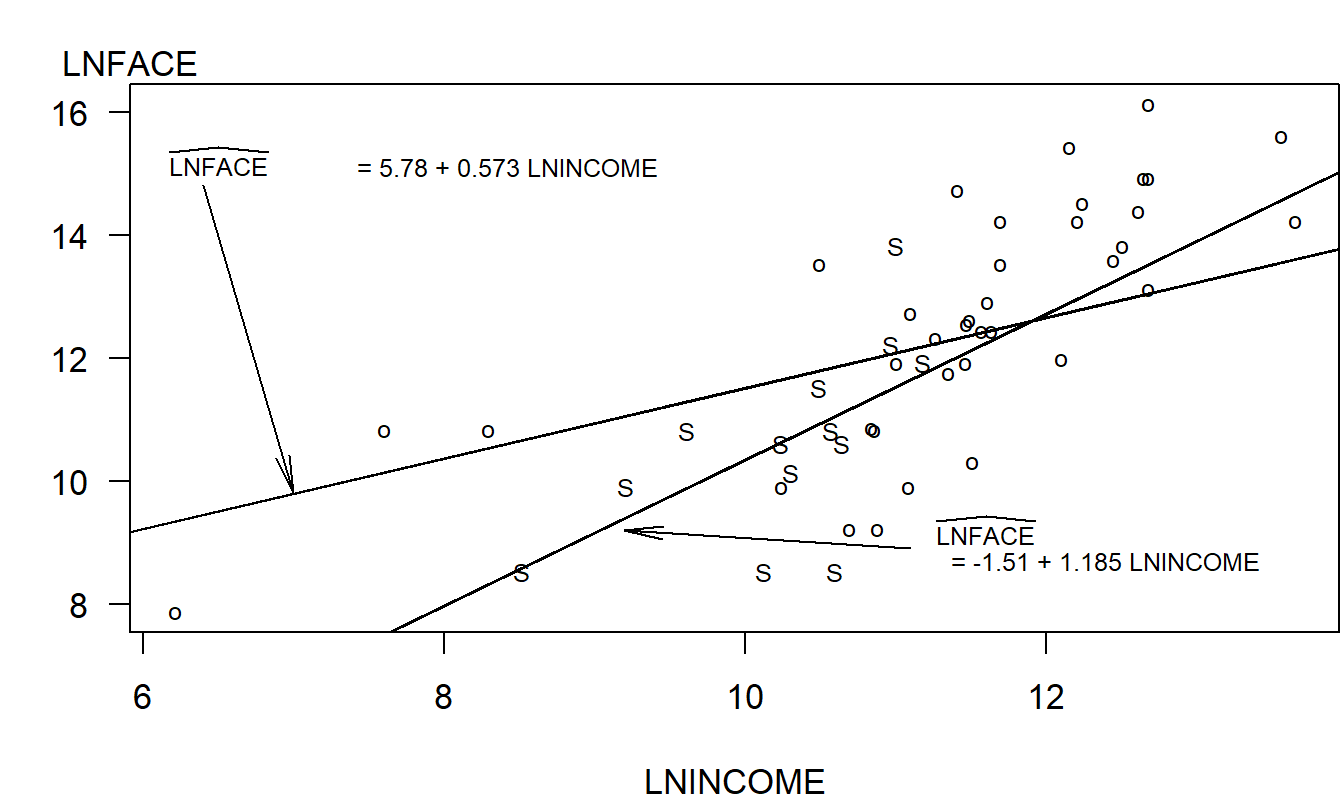
Gráfico de LNFACE versus LNINCOME, con el código de letra S para solteros y o para otros. Las líneas de regresión ajustadas han sido superpuestas. La línea inferior es para solteros y la línea superior es para otros.

Figura 3.7: Gráfico de LNFACE versus LNINCOME, con el código de letra S para solteros y o para otros. Las líneas de regresión ajustadas han sido superpuestas. La línea inferior es para solteros y la línea superior es para otros.

Ejemplo: Gastos de Compañías de Seguros de Vida. En una industria de seguros de vida bien desarrollada, minimizar los gastos es crucial para la posición competitiva de una compañía. Segal (2002) analizó datos contables anuales de más de 100 empresas para el período 1995-1998, inclusive, utilizando una base de datos de la Asociación Nacional de Comisionados de Seguros (NAIC) y otra información reportada. Segal modeló los gastos generales de la compañía como una función de la producción de la empresa y el precio de los insumos. La producción consiste en la producción de seguros, medida por $x_1$ a $x_5$, descritos en Tabla 3.10. Segal también consideró el cuadrado de cada salida, así como un término de interacción con una variable binaria $D$ que indica si la empresa utiliza o no una sucursal para distribuir sus productos. (En una sucursal, los gerentes de campo son empleados de la empresa, no agentes independientes.)

Tabla 3.10.Veintitrés Coeficientes de Regresión de un Modelo de Costos de Gastos

\[ \small{ \begin{array}{l|rrrr} \hline & \text{Variable} & &\text{Variable}&\text{ Cuadrada} \\ & \text{Base} & \text{Interacción} & \text{Base} & \text{Interacción} \\ & & \text{con}~~ & & \text{con}~~ \\ \text{Variable} & (D=0) & (D=1) & (D=0) & (D=1)\\ \hline \text{Número de Pólizas de Vida Emitidas } (x_1) & -0.454 & 0.152 & 0.032 & -0.007 \\ \text{Cantidad de Seguro de Vida a Término Vendido } (x_2) & 0.112 & -0.206 & 0.002 & 0.005 \\ \text{Cantidad de Seguro de Vida Entera Vendido } (x_3) & -0.184 & 0.173 & 0.008 & -0.007 \\ \text{Total de Consideraciones de Anualidades } (x_4) & 0.098 & -0.169 & -0.003 & 0.009 \\ \text{Total de Primas de Accidentes y Salud } (x_5) &-0.171 & 0.014 & 0.010 & 0.002 \\ \text{Intercepto } & 7.726 & & & \\ \text{Precio del Trabajo (PL)} & 0.553 & & & \\ \text{Precio del Capital (PC)} & 0.102 & & & \\ \hline \end{array} \\ \begin{array}{l} \textit{Nota: } x_1 \text{ a } x_5 \text{ están en unidades logarítmicas}.\\ \textit{Fuente: Segal (2002)} \end{array} } \]

Para los insumos de precios, el precio del trabajo ($PL$) se define como el costo total de empleados y agentes dividido por su número, en unidades logarítmicas. El precio del capital ($PC$) se aproxima por la relación del gasto en capital con el número de empleados y agentes, también en unidades logarítmicas. El precio de los materiales consiste en gastos distintos al trabajo y al capital divididos por el número de pólizas vendidas y terminadas durante el año. No aparece directamente como una variable explicativa. Más bien, Segal tomó la variable dependiente ($y$) como los gastos totales de la compañía divididos por el precio de los materiales, nuevamente en unidades logarítmicas.

Con estas definiciones de variables, Segal estimó la siguiente función de regresión:

\[ \mathrm{E~}y=\beta_0 + \sum_{j=1}^5 \left( \beta_j x_j + \beta_{j+5} D x_j + \beta_{j+10} x_j^2 + \beta_{j+15}D x_j^2 \right) + \beta_{21} PL + \beta_{22} PC. \]

Las estimaciones de los parámetros aparecen en Tabla 3.10. Por ejemplo, el cambio marginal en $\mathrm{E}~y$ por unidad de cambio en $x_1$ es:

\[ \frac{\partial ~ \mathrm{E}~y}{\partial x_1}= \beta_1 + \beta_{6} D + 2 \beta_{11} x_1 + 2 \beta_{16}D x_1, \]

que se estima como $-0.454 + 0.152 D + (0.064 - 0.014 D) x_1$. Para estos datos, el número mediano de pólizas emitidas fue $x_1=15,944$. En este valor de $x_1$, el cambio marginal estimado es $-0.454 + 0.152 D + (0.064 - 0.014 D) \mathrm{ln}(15944) = 0.165 + 0.017 D,$ o 0.165 para la base $(D=0)$ y 0.182 para compañías de sucursales $(D=1)$.

Estas estimaciones son elasticidades, como se define en la Sección 3.2.2. Para interpretar estos coeficientes más a fondo, dejemos que $COST$ represente los gastos generales totales de la compañía y $NUMPOL$ represente el número de pólizas de vida emitidas. Entonces, para compañías de sucursales $(D=1)$, tenemos:

\[ 0.182 \approx \frac{\partial y }{\partial x_1 } = \frac{\partial ~ \mathrm{ln}~COST}{\partial ~ \mathrm{ln}~NUMPOL}= \frac{ \frac{\partial ~ COST}{\partial ~NUMPOL}} {\frac{COST}{NUMPOL}}, \]

o $\frac{\partial ~ COST}{\partial ~NUMPOL} \approx 0.182 \frac{COST}{NUMPOL}$. El costo mediano es $15,992,000, por lo que el costo marginal por póliza en estos valores medianos es $0.182 \times (15992000/15944) =$ $182.55.

Caso Especial: Funciones de Respuesta Curvilíneas

Podemos expandir las funciones polinómicas de una variable explicativa para incluir varias variables explicativas. Por ejemplo, la respuesta esperada, o función de respuesta, para un modelo de segundo orden con dos variables explicativas es:

\[ \mathrm{E} y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_{11} x_1^2 + \beta_{22} x_2^2 + \beta_{12} x_1 x_2. \]

La Figura 3.8 ilustra esta función de respuesta. De manera similar, la función de respuesta para un modelo de segundo orden con tres variables explicativas es:

\[ \mathrm{E} y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + \beta_{11} x_1^2 + \beta_{22} x_2^2 + \beta_{33} x_3^2 + \beta_{12} x_1 x_2 + \beta_{13} x_1 x_3 + \beta_{23} x_2 x_3. \]

Cuando hay más de una variable explicativa, los modelos de tercer orden y de órdenes superiores rara vez se utilizan en aplicaciones.

$Gráfico de $\mathrm{E}~y = \beta_0 + \beta_1~x_1 + \beta_2~x_2 + \beta_{11}~x_1^2 + \beta_{22}~x_2^2 + \beta_{12}~x_1~x_2$ versus $x_1$ y $x_2$.$

Figura 3.8: Gráfico de $\mathrm{E}~y = \beta_0 + \beta_1~x_1 + \beta_2~x_2 + \beta_{11}~x_1^2 + \beta_{22}~x_2^2 + \beta_{12}~x_1~x_2$ versus $x_1$ y $x_2$.

Código R para producir la Figura 3.8

Caso Especial: Funciones No Lineales de una Variable Continua

En algunas aplicaciones, esperamos que la respuesta tenga cambios abruptos en el comportamiento en ciertos valores de una variable explicativa, incluso si la variable es continua. Por ejemplo, supongamos que estamos tratando de modelar las contribuciones benéficas de un individuo ($y$) en función de sus ingresos ($x$). Para los datos de 2007, un modelo simple que podríamos considerar es el que se muestra en la Figura 3.9.

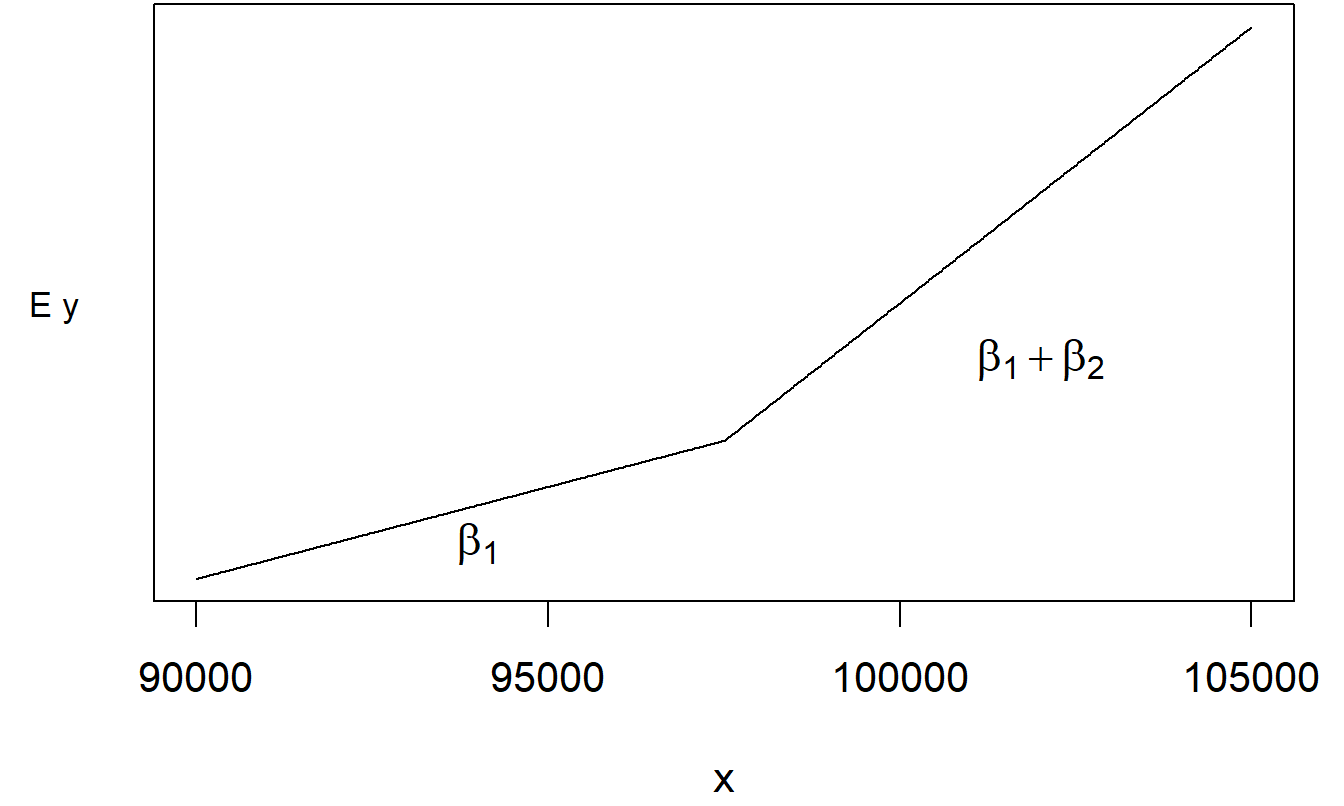
$El cambio marginal en $\mathrm{E}~y$ es menor por debajo de $97,500. El parámetro $\beta_2$ representa la diferencia en las pendientes.$

Figura 3.9: El cambio marginal en $\mathrm{E}~y$ es menor por debajo de $97,500. El parámetro $\beta_2$ representa la diferencia en las pendientes.

Código R para producir la Figura 3.9

Una justificación para este modelo es que, en 2007, los individuos pagaban un 7.65% de sus ingresos en impuestos de Seguridad Social hasta $97,500. No se aplican impuestos de Seguridad Social a los ingresos que superan los $97,500. Así, una teoría es que, para los ingresos superiores a $97,500, los individuos tienen más ingresos disponibles por dólar y, por lo tanto, deberían estar más dispuestos a hacer contribuciones benéficas.

Para modelar esta relación, definamos la variable binaria $z$ que sea cero si $x < 97,500$ y uno si $x \ge 97,500$. Definamos la función de regresión como $\mathrm{E}~y = \beta_0 + \beta_1 x + \beta_2 z (x - 97,500)$. Esto se puede escribir como:

\[ \mathrm{E}~y = \begin{cases} \beta_0 + \beta_1 x & x < 97,500 \\ \beta_0 - \beta_2(97,500) + (\beta_1+\beta_2) x & x \geq 97,500 \end{cases} \]

Para estimar este modelo, realizaríamos una regresión de $y$ sobre dos variables explicativas, $x_1 = x$ y $x_2 = z \times (x - 97,500)$. Si $\beta_2 > 0$, entonces la tasa marginal de contribuciones benéficas es mayor para ingresos que superan los $97,500.

La Figura 3.9 ilustra esta relación, conocida como regresión lineal por tramos o a veces un modelo de “barra rota”. El cambio abrupto en la Figura 3.9 en $x = 97,500$ se llama “cambio de pendiente”. Tenemos relaciones lineales por encima y por debajo del cambio de pendiente y hemos usado una variable binaria para unir las dos partes. No estamos restringidos a un solo cambio de pendiente. Por ejemplo, supongamos que deseamos hacer un estudio histórico de los ingresos gravables federales para los contribuyentes solteros de 1992. Entonces, había tres tramos impositivos: la tasa marginal por debajo de 21,450 era del 15%, por encima de 51,900 era del 31%, y en medio era del 28%. Para este ejemplo, usaríamos dos cambios de pendiente, en 21,450 y 51,900.

Además, la regresión lineal por tramos no está restringida a funciones de respuesta continuas. Por ejemplo, supongamos que estamos estudiando las comisiones pagadas a los corredores de bolsa ($y$) en función del número de acciones compradas por un cliente ($x$). Podríamos esperar ver la relación ilustrada en la Figura 3.10. Aquí, la discontinuidad en $x = 100$ refleja los gastos administrativos de comerciar en lotes irregulares, ya que se llaman transacciones de menos de 100 acciones. El menor costo marginal para transacciones superiores a 100 acciones simplemente refleja las economías de escala al hacer negocios en volúmenes mayores. Un modelo de regresión para esto es $\mathrm{E}~y = \beta_0 + \beta_1 x + \beta_2 z + \beta_3 z x$ donde $z = 0$ si $x < 100$ y $z = 1$ si $x \geq 100$. La función de regresión representada en la Figura 3.10 es:

\[ \mathrm{E}~y = \begin{cases} \beta_0 + \beta_1 x_1 & x < 100 \\ \beta_0 + \beta_2 + (\beta_1+\beta_3) x_1 & x \geq 100 \end{cases} \]

$Gráfico de comisiones esperadas ($\mathrm{E}~y$) versus número de acciones negociadas ($x$). El cambio en $x=100$ refleja ahorros en gastos administrativos. La pendiente más baja para $x \ge 100$ refleja economías de escala en gastos.$

Figura 3.10: Gráfico de comisiones esperadas ($\mathrm{E}~y$) versus número de acciones negociadas ($x$). El cambio en $x=100$ refleja ahorros en gastos administrativos. La pendiente más baja para $x \ge 100$ refleja economías de escala en gastos.

Código R para producir la Figura 3.10

3.6 Lectura Adicional y Referencias

Para las pruebas de los resultados del Capítulo 3, remitimos al lector a Goldberger (1991). Los modelos de regresión no lineales se discuten, por ejemplo, en Bates y Watts (1988).

El Capítulo 3 ha introducido los fundamentos de la regresión lineal múltiple. El Capítulo 4 ampliará el alcance al introducir variables categóricas y métodos de inferencia estadística para manejar varios coeficientes simultáneamente. El Capítulo 5 presentará técnicas para ayudarte a seleccionar variables apropiadas en un modelo de regresión lineal múltiple. El Capítulo 6 es un capítulo de síntesis, que discute la interpretación del modelo, la selección de variables y la recolección de datos.

Referencias del Capítulo

Bates, Douglas M. y Watts, D. G. (1988). Nonlinear Regression Analysis and its Applications. John Wiley & Sons, Nueva York.
Lemaire, Jean (2002). Why do females live longer than males? North American Actuarial Journal, 6(4), 21-37.
Goldberger, Arthur (1991). A Course in Econometrics. Harvard University Press, Cambridge.
Plackett, R.L. (1960). Regression Analysis. Clarendon Press, Oxford, Inglaterra.
Segal, Dan (2002). An economic analysis of life insurance company expenses. North American Actuarial Journal, 6(4), 81-94.

3.7 Ejercicios

3.1. Considera un conjunto de datos ficticio de $n = 100$ observaciones con $s_y = 100$. Realizamos una regresión con tres variables explicativas para obtener $s = 50$.

Calcula el coeficiente de determinación ajustado, $R_a^2$.
Completa la tabla de ANOVA.

\[ \small{ \begin{array}{|l|l|c|l|} \hline \text{Tabla de ANOVA} \\ \hline \text{Fuente} & \text{Suma de Cuadrados} & \text{df} & \text{Cuadrado Medio} \\ \hline \text{Regresión} & & & \\ \text{Error} & & & \\ \text{Total} & & & \\ \hline \end{array} } \]

Calcula el coeficiente de determinación (no ajustado), $R^2$.

3.2. Considera un conjunto de datos ficticio de $n = 100$ observaciones con $s_y = 80$. Realizamos una regresión con tres variables explicativas para obtener $s = 50$. También obtenemos

\[ \small{ \left(\mathbf{X^{\prime} X} \right)^{-1} = \begin{pmatrix} 100 & 20 & 20 & 20 \\ 20 & 90 & 30 & 40 \\ 20 & 30 & 80 & 50 \\ 20 & 40 & 50 & 70 \\ \end{pmatrix}. } \]

Determina el error estándar de $b_3$, $se(b_3)$.
Determina la covarianza estimada entre $b_2$ y $b_3$.
Determina la correlación estimada entre $b_2$ y $b_3$.
Determina la varianza estimada de $4b_2 + 3b_3$.

3.3. Considera el siguiente pequeño conjunto de datos ficticio. Ajustarás un modelo de regresión a $y$ usando dos variables explicativas, $x_1$ y $x_2$.

\[ \small{ \begin{array}{c|cccc} \hline i & 1 & 2 & 3 & 4 \\ \hline x_{i,1} & -1 & 2 & 4 & 6 \\ x_{i,2} & 0 & 0 & 1 & 1 \\ y_i & 0 & 1 & 5 & 8 \\ \hline \end{array} } \]

A partir del modelo de regresión ajustado, tenemos $s = 1.373$ y

\[ \small{ \mathbf{b} = \begin{pmatrix} 0.1538 \\ 0.6923 \\ 2.8846 \end{pmatrix} ~~~\text{y}~~~ \left(\mathbf{X^{\prime} X} \right)^{-1} = \begin{pmatrix} 0.53846 & -0.07692 & -0.15385 \\ -0.07692 & 0.15385 & -0.69231 \\ -0.15385 & -0.69231 & 4.11538 \\ \end{pmatrix}. } \]

Escribe el vector de variables dependientes, $\mathbf{y}$, y la matriz de variables explicativas, $\mathbf{X}$.
Determina el valor numérico para $\widehat{y}_3$, el valor ajustado para la tercera observación.
Determina el valor numérico para $se(b_2)$.
Determina el valor numérico para $t(b_1)$.

3.4. Lotería de Wisconsin. La Sección 2.1 describió una muestra de $n=50$ áreas geográficas (códigos postales) que contenían datos de ventas de la lotería estatal de Wisconsin ($y = \text{SALES}$). En esa sección, las ventas se analizaron usando un modelo de regresión lineal básico con $x = \text{POP}$, la población del área, como la variable explicativa. Este ejercicio amplía ese análisis al introducir variables explicativas adicionales dadas en la Tabla 3.11.

\[ \text{Tabla 3.11: Características de lotería, económicas y demográficas de cincuenta códigos postales de Wisconsin} \]

\[ \small{ \begin{array}{ll} \hline \textbf{Características de la lotería} \\ \hline \text{SALES} & \text{Ventas de lotería en línea a consumidores individuales} \\ \hline \textbf{Características económicas y } \\ ~~~~~\textbf{demográficas} \\\hline \text{PERPERHH} & \text{Personas por hogar} \\ \text{MEDSCHYR} & \text{Años medianos de escolaridad} \\ \text{MEDHVL} & \text{Valor medianos de viviendas en \$1000s para viviendas ocupadas por sus propietarios} \\ \text{PRCRENT} & \text{Porcentaje de viviendas ocupadas por arrendatarios} \\ \text{PRC55P} & \text{Porcentaje de la población que tiene 55 años o más} \\ \text{HHMEDAGE} & \text{Edad mediana del hogar} \\ \text{MEDINC} & \text{Ingreso mediano estimado del hogar, en \$1000s} \\ \text{POP} & \text{Población} \\ \hline \end{array} } \]

Produce una tabla de estadísticas descriptivas para todas las variables. Un código postal (observación 11, código = 53211, Shorewood Wisconsin, un suburbio de Milwaukee) parece tener valores inusualmente grandes de MEDSCHYR y MEDHVL. Para esta observación, ¿cuántas desviaciones estándar está el valor de MEDSCHYR por encima de la media? Para esta observación, ¿cuántas desviaciones estándar está el valor de MEDHVL por encima de la media?
Produce una tabla de correlaciones. ¿Cuáles son las tres variables más correlacionadas con SALES?
Produce una matriz de gráficos de dispersión de todas las variables explicativas y SALES. En el gráfico de MEDSCHYR versus SALES, describe la posición de la observación 11.
Ajusta un modelo lineal de SALES en las ocho variables explicativas. Resume el ajuste de este modelo citando la desviación estándar de los residuos, $s$, el coeficiente de determinación, $R^2$ y su versión ajustada, $R_a^2$.
Basado en el ajuste del modelo de la parte (d), ¿es MEDSCHYR una variable estadísticamente significativa? Para responder a esta pregunta, utiliza una prueba formal de hipótesis. Expón tus hipótesis nula y alternativa, criterio de decisión y regla de decisión.
Ahora ajusta un modelo más parsimonioso, usando SALES como variable dependiente y MEDSCHYR, MEDHVL y POP como variables explicativas. Resume el ajuste de este modelo citando la desviación estándar de los residuos, $s$, el coeficiente de determinación, $R^2$ y su versión ajustada, $R_a^2$. ¿Cómo se comparan estos valores con el ajuste del modelo en la parte (d)?
Observa que el signo del coeficiente de regresión asociado con MEDSCHYR es negativo. Para ayudar a interpretar este coeficiente, calcula el coeficiente de correlación parcial correspondiente. ¿Cuál es la interpretación de este coeficiente?
Para obtener más información sobre la relación entre MEDSCHYR y SALES, produce un gráfico de variable añadida controlando los efectos de MEDHVL y POP. Verifica que la correlación asociada con este gráfico concuerde con tu respuesta en la parte (g).
Vuelve a ejecutar la regresión en la parte (f), después de eliminar la observación 11. Cita las estadísticas descriptivas básicas de esta regresión. Para este ajuste del modelo, ¿es MEDSCHYR una variable estadísticamente significativa? Para responder a esta pregunta, utiliza una prueba formal de hipótesis. Expón tus hipótesis nula y alternativa, criterio de decisión y regla de decisión.
Vuelve a ejecutar la regresión en la parte (f), después de eliminar la observación 9. Cita las estadísticas descriptivas básicas de esta regresión.

3.5. Gastos de Compañías de Seguros. Este ejercicio considera los datos de compañías de seguros del NAIC y descritos en el Ejercicio 1.6.

La Tabla 3.10 describe varias variables que pueden ser usadas para explicar los gastos. Al igual que en el estudio de Segal (2002) sobre los aseguradores de vida, los “outputs” de la empresa consisten en primas emitidas (para propiedad y accidentes, estas se subdividen en líneas personales y comerciales) así como pérdidas (subdivididas en líneas de corto y largo plazo). ASSETS y CASH son medidas comúnmente usadas del tamaño de una empresa. GROUP, STOCK y MUTUAL describen la estructura organizacional. Los “inputs” de la empresa se recopilaron del Bureau of Labor Statistics (BLS, del programa Occupational Employee Statistics). STAFFWAGE se calcula como el salario promedio en el estado donde está ubicada la compañía de seguros. AGENTWAGE se calcula como el salario promedio ponderado de la industria de corretaje, ponderado por el porcentaje de prima bruta escrita en cada estado.

Tabla 3.10: **Variables de Gastos de Aseguradoras**
Variable	Descripción
EXPENSES	Gastos totales incurridos, en millones de dólares
LOSSLONG	Pérdidas incurridas para líneas de largo plazo, en millones de dólares
LOSSSHORT	Pérdidas incurridas para líneas de corto plazo, en millones de dólares
GPWPERSONAL	Prima bruta emitida para líneas personales, en millones de dólares
GPWCOMM	Prima bruta emitida para líneas comerciales, en millones de dólares
ASSETS	Activos netos admitidos, en millones de dólares
CASH	Efectivo y activos invertidos, en millones de dólares
GROUP	Indica si la empresa está afiliada
STOCK	Indica si la empresa es una compañía de acciones
MUTUAL	Indica si la empresa es una compañía mutua
STAFFWAGE	Salario promedio anual del personal administrativo de la aseguradora, en miles de dólares
AGENTWAGE	Salario promedio anual del agente de seguros, en miles de dólares

Una inspección preliminar de los datos mostró que muchas empresas no informaron pérdidas de seguros en 2005. Para este ejercicio, consideramos las 384 compañías con algunas pérdidas en el archivo NAICExpense.csv.

Produce estadísticas descriptivas de la variable de respuesta y las variables explicativas (no binarias). Nota el patrón de sesgo para cada variable. Observa que muchas variables tienen valores negativos.
Transforma cada variable no binaria mediante la transformación logarítmica modificada, $\ln(1+x)$. Produce estadísticas descriptivas de estas variables explicativas no binarias modificadas. Denota LNEXPENSES ($= \ln(1+\text{EXPENSES})$) como la variable de gastos modificada.
Para el análisis posterior, usa solo las variables modificadas descritas en la parte (b).
Produce una tabla de correlaciones para las variables no binarias. ¿Cuáles son las tres variables más correlacionadas con LNEXPENSES?
Proporciona un diagrama de caja de LNEXPENSES por nivel de GROUP. ¿Qué nivel de grupo tiene mayores gastos?
Ajusta un modelo lineal de LNEXPENSES en las once variables explicativas. Resume el ajuste de este modelo citando la desviación estándar de los residuos, $s$, el coeficiente de determinación, $R^2$, y su versión ajustada, $R^2_a$.
Ajusta un modelo lineal de LNEXPENSES en un modelo reducido usando ocho variables explicativas, eliminando LNCASH, STOCK y MUTUAL. Para las variables explicativas, incluye ASSETS, GROUP, ambas versiones de pérdidas y primas brutas, así como las dos variables del BLS.

f(i). Resume el ajuste de este modelo citando $s$, $R^2$, y $R^2_a$.
f(ii). Interpreta el coeficiente asociado con las primas brutas comerciales en la escala logarítmica.
f(iii). Supón que GPWCOMM aumenta en $1, ¿cuánto esperamos que aumenten los EXPENSES? Usa tu respuesta en la parte f(ii) y los valores medianos de GPWCOMM y EXPENSES para esta pregunta.
Eleva al cuadrado cada una de las dos variables de pérdidas y las dos de primas brutas. Ajusta un modelo lineal de LNEXPENSES en un modelo reducido usando doce variables explicativas, las ocho variables de la parte (f) y los cuatro términos cuadrados adicionales que acabas de crear.
g(i). Resume el ajuste de este modelo citando $s$, $R^2$, y $R^2_a$.
g(ii). ¿Los términos cuadráticos parecen ser variables explicativas útiles?
Ahora omite las dos variables del BLS, por lo que estás ajustando un modelo de LNEXPENSES en ASSETS, GROUP, ambas versiones de pérdidas y primas brutas, así como términos cuadráticos. Resume el ajuste de este modelo citando $s$, $R^2$, y $R^2_a$. Comenta sobre el número de observaciones usadas para ajustar este modelo comparado con la parte (f).
Términos de Interacción
Elimina los términos cuadráticos de la parte (g) y agrega términos de interacción con la variable ficticia GROUP. Así, ahora hay once variables: ASSETS, GROUP, ambas versiones de pérdidas y primas brutas, así como interacciones de GROUP con ASSETS y ambas versiones de pérdidas y primas brutas.
i(i). Resume el ajuste de este modelo citando $s$, $R^2$, y $R^2_a$.
i(ii). Supón que GPWCOMM aumenta en $1, ¿cuánto esperamos que aumenten los EXPENSES para las compañías GROUP=0? Usa los valores medianos de GPWCOMM y EXPENSES de las compañías GROUP=0 para esta pregunta.
i(iii). Supón que GPWCOMM aumenta en $1, ¿cuánto esperamos que aumenten los EXPENSES para las compañías GROUP=1? Usa los valores medianos de GPWCOMM y EXPENSES de las compañías GROUP=1 para esta pregunta.

3.6 Expectativas de Vida Nacionales. Continuamos el análisis iniciado en los Ejercicios 1 y 2. Ahora ajusta un modelo de regresión en LIFEEXP usando tres variables explicativas: FERTILITY, PUBLICEDUCATION y lnHEALTH (la transformación logarítmica natural de PRIVATEHEALTH).

Interpreta el coeficiente de regresión asociado con PUBLICEDUCATION.
Interpreta el coeficiente de regresión asociado con los gastos en salud sin usar la escala logarítmica para los gastos.
Basado en el ajuste del modelo, ¿es PUBLICEDUCATION una variable estadísticamente significativa? Para responder a esta pregunta, usa una prueba formal de hipótesis. Expón tus hipótesis nula y alternativa, criterio de decisión, y regla de decisión.
El signo negativo del coeficiente de PUBLICEDUCATION es sorprendente, dado que el signo de la correlación entre PUBLICEDUCATION y LIFEEXP es positivo y la intuición sugiere una relación positiva. Para verificar este resultado, aparece un gráfico de variable añadida en la Figura 3.11.
d(i). Para un gráfico de variable añadida, describe su propósito y un método para producirlo.
d(ii). Calcula la correlación correspondiente al gráfico de variable añadida que aparece en la Figura 3.11.

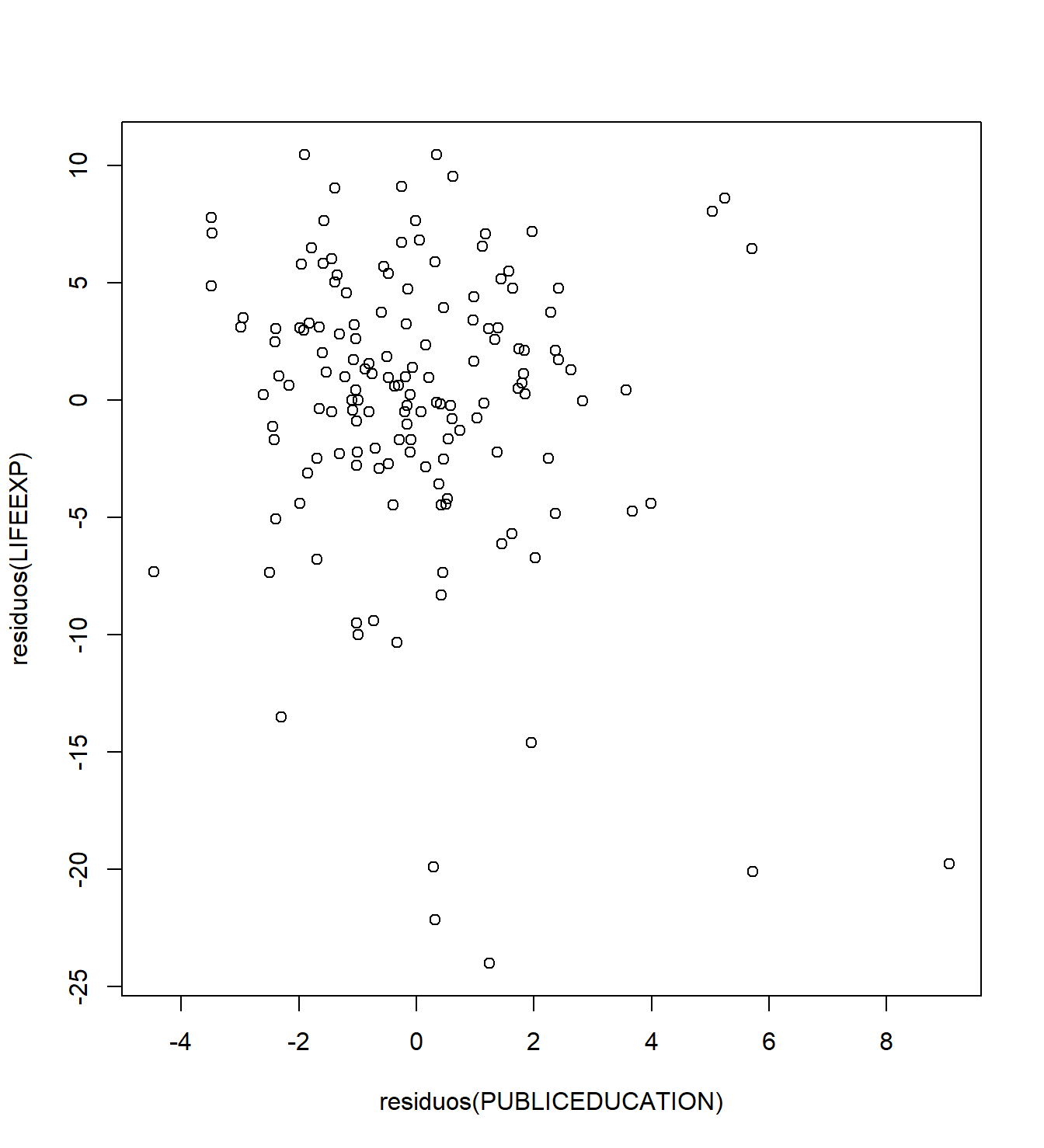
Figura 3.11: Gráfico de variable añadida de PUBLICEDUCATION versus LIFEEXP, controlando por FERTILITY y lnHEALTH

Modelado de Regresión con Aplicaciones Actuariales y Financieras