Capítulo 8 Autocorrelaciones y Modelos Autorregresivos

Vista previa del capítulo. Este capítulo continúa nuestro estudio de los datos de series temporales. El Capítulo 7 introdujo técnicas para determinar patrones principales que proporcionan un buen primer paso para los pronósticos. El Capítulo 8 presenta técnicas para detectar tendencias sutiles en el tiempo y modelos para acomodar estas tendencias. Estas técnicas detectan y modelan relaciones entre los valores actuales y pasados de una serie utilizando conceptos de regresión.

8.1 Autocorrelaciones

Aplicación: Retornos de Bonos con Inflación

Para motivar los métodos introducidos en este capítulo, trabajamos en el contexto de la serie de retornos de bonos con inflación. A partir de enero de 2003, el Departamento del Tesoro de los Estados Unidos estableció un índice de bonos con inflación que resume los retornos de bonos a largo plazo ofrecidos por el Departamento del Tesoro que están indexados por inflación. Para un bono protegido contra la inflación del Tesoro (TIPS), el principal del bono está indexado al valor (con un rezago de tres meses) del índice de precios al consumidor (no ajustado estacionalmente). Luego, el bono paga un cupón semestral a una tasa determinada en la subasta cuando se emite el bono. El índice que examinamos es el promedio no ponderado de las ofertas para todos los TIPS con plazos restantes de vencimiento de 10 o más años.

Se consideran valores mensuales del índice desde enero de 2003 hasta marzo de 2007, para un total de $T=51$ retornos. Un gráfico de series temporales de los datos se presenta en la Figura 8.1. Este gráfico sugiere que la serie es estacionaria, por lo que es útil examinar la distribución de la serie a través de estadísticas resumidas que aparecen en Tabla 8.1.

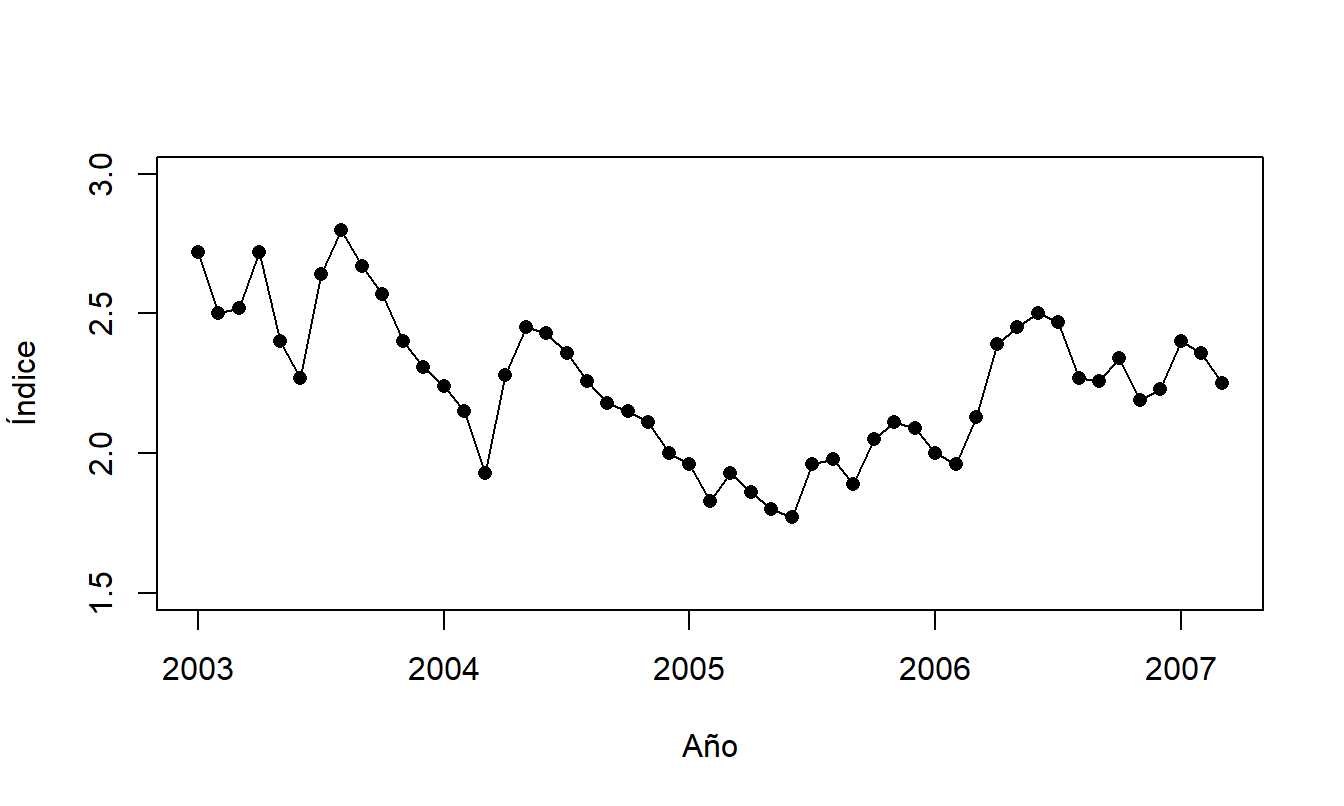
Figura 8.1: Gráfico de Series Temporales del Índice de Bonos con Inflación. Valores mensuales de enero de 2003 a marzo de 2007, inclusive.

Tabla 8.1. Estadísticas Resumidas del Índice de Bonos con Inflación

\[ \small{ \begin{array}{lccccc} \hline & & & \text{Desviación} & & \\ \text{Variable} & \text{Media} & \text{Mediana} & \text{Estándar} & \text{Mínimo} & \text{Máximo} \\ \hline \text{ÍNDICE} & 2.245 & 2.26 & 0.259 & 1.77 & 2.80 \\ \hline ~~~Fuente: \text{Tesoro de los EE.UU.} \end{array} } \]

Código R para producir la Figura 8.1 y la Tabla 8.1

Mean	Median	Std	Minimum	Maximum
2.2449	2.26	0.2589	1.77	2.8

Nuestro objetivo es detectar patrones en los datos y proporcionar modelos para representar estos patrones. Aunque la Figura 8.1 muestra una serie estacionaria sin tendencias importantes, algunos patrones sutiles son evidentes. A partir de mediados de 2003 y luego a principios de 2004, vemos grandes incrementos seguidos por una serie de disminuciones en el índice. A partir de 2005, parece estar ocurriendo un patrón de incremento con algún comportamiento cíclico. Aunque no está claro qué fenómeno económico representan estos patrones, no es lo que esperaríamos ver en un proceso de ruido blanco. Para un proceso de ruido blanco, una serie puede aumentar o disminuir al azar de un período al siguiente, produciendo una serie no suave, “irregular” a lo largo del tiempo.

Para ayudar a entender estos patrones, la Figura 8.2 presenta un diagrama de dispersión de la serie ($y_t$) frente a su valor rezagado ($y_{t-1}$). Dado que este es un paso crucial para entender este capítulo, la Tabla 8.2 presenta un pequeño subconjunto de los datos para que puedas ver exactamente qué representa cada punto en el diagrama de dispersión. La Figura 8.2 muestra una fuerte relación entre $y_t$ y $y_{t-1}$; modelaremos esta relación en la siguiente sección.

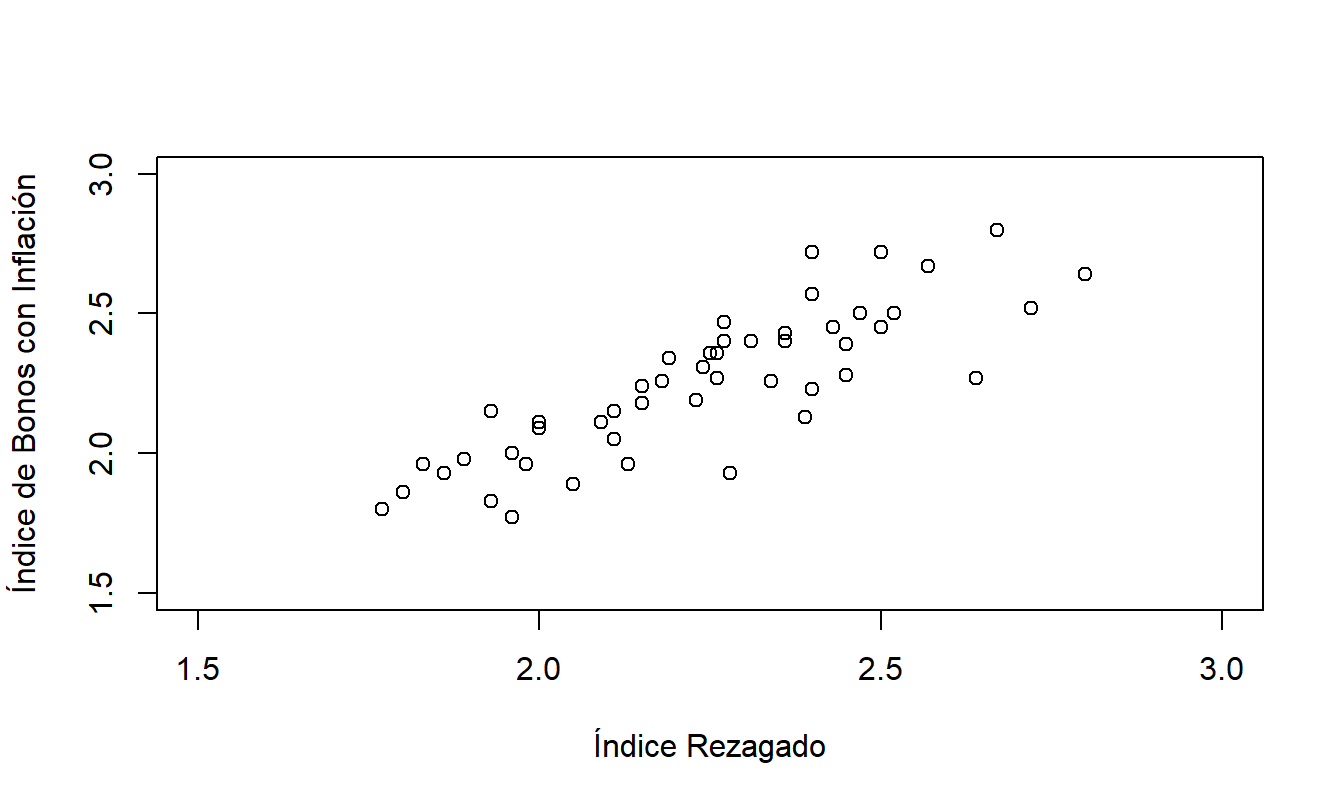
Índice de Bonos con Inflación frente a Valor Rezagado. Este diagrama de dispersión revela una relación lineal entre el índice y su valor rezagado.

Figura 8.2: Índice de Bonos con Inflación frente a Valor Rezagado. Este diagrama de dispersión revela una relación lineal entre el índice y su valor rezagado.

Tabla 8.2. Índice y Valor Rezagado para los Primeros Cinco de $T=51$ Valores

\[ \small{ \begin{array}{l|crrrr} \hline t & 1~~ & 2~~ & 3~~ & 4~~ & 5~~ \\ \hline \text{Índice }(y_t) & 2.72 & 2.50 & 2.52 & 2.72 & 2.40 \\ \text{Índice Rezagado } (y_{t-1}) & * & 2.72 & 2.50 & 2.52 & 2.72 \\ \hline \end{array} } \]

Código R para producir la Figura 8.2

# Figura 82
#inflation  <- read.csv("CSVData/InflationBond.csv", header=TRUE)
#inflation  <- read.csv("../../CSVData/InflationBond.csv", header=TRUE)
#index <- inflation$INFBOND

n <- length(index)
plot(index[-1], index[-n], xlim=c(1.5,3.0), ylim=c(1.5,3.0),
     xlab="Índice Rezagado", ylab="Índice de Bonos con Inflación")

Autocorrelaciones

Los diagramas de dispersión son útiles porque muestran gráficamente relaciones no lineales, así como lineales, entre dos variables. Como establecimos en el Capítulo 2, las correlaciones pueden usarse para medir la relación lineal entre dos variables. Recuerda que al tratar con datos transversales, resumimos relaciones entre {$y_t$} y {$x_t$} usando la estadística de correlación: \[ r = \frac{1}{(T-1)s_{x}s_y} \sum_{t=1}^{T} \left( x_t - \overline{x}\right) \left( y_t-\overline{y} \right) . \] Ahora imitamos esta estadística usando la serie {$y_{t-1}$} en lugar de {$x_t$}. Con este reemplazo, usa $\overline{y}$ en lugar de $\overline{x}$ y, para el denominador, usa $s_y$ en lugar de $s_x$. Con esta última sustitución, tenemos $(T-1) s_y^2 = \sum_{t=1}^{T}(y_t-\overline{y})^2$. Nuestra estadística de correlación resultante es:

\[ r_1 = \frac{\sum_{t=2}^{T} \left( y_{t-1}-\overline{y}\right) \left( y_t- \overline{y}\right) }{\sum_{t=1}^{T} (y_t-\overline{y})^2}. \]

Esta estadística se conoce como autocorrelación, es decir, una correlación de la serie consigo misma. Esta estadística resume la relación lineal entre {$y_t$} y {$y_{t-1}$}, es decir, observaciones que están separadas por una unidad de tiempo. También será útil resumir la relación lineal entre observaciones que están separadas por $k$ unidades de tiempo, {$y_t$} y {$y_{t-k}$}, de la siguiente manera.

Definición. La estadística de autocorrelación rezagada en k es:

\[ r_k = \frac{\sum_{t=k+1}^{T}\left( y_{t-k}-\overline{y}\right) \left( y_t- \overline{y}\right) }{\sum_{t=1}^{T}(y_t-\overline{y})^2}, ~~~~k=1,2, \ldots \]

Las propiedades de las autocorrelaciones son similares a las correlaciones. Al igual que con la estadística de correlación usual $r$, el denominador, $\sum_{t=1}^{T}(y_t - \overline{y})^2$, siempre es no negativo y, por lo tanto, no cambia el signo del numerador. Usamos este dispositivo de reescalado para que $r_k$ siempre esté dentro del intervalo [-1, 1]. Así, al interpretar $r_k$, un valor cercano a -1, 0 y 1 significa, respectivamente, una relación negativa fuerte, casi nula o positiva fuerte entre $y_t$ y $y_{t-k}$. Si existe una relación positiva entre $y_t$ y $y_{t-1}$, entonces $r_1 > 0$ y el proceso se dice positivamente autocorrelacionado. Por ejemplo, en la Tabla 8.3 se muestran las primeras cinco autocorrelaciones de la serie de bonos con inflación. Estas autocorrelaciones indican que existe una relación positiva entre observaciones adyacentes.

Tabla 8.3. Autocorrelaciones para la Serie de Bonos con Inflación

\[ \small{ \begin{array}{l|ccccc} \hline \text{Rezago } k & 1 & 2 & 3 & 4 & 5 \\ \hline \text{Autocorrelación } r_k & 0.814 & 0.632 & 0.561 & 0.447 & 0.367 \\ \hline \end{array} } \]

Código R para producir la Tabla 8.3

x
1.000
0.814
0.632
0.561
0.447
0.367

8.2 Modelos Autorregresivos de Orden Uno

Definición y Propiedades del Modelo

En la Figura 8.2 notamos la fuerte relación entre los valores pasados inmediatos y los valores actuales del índice de bonos con inflación. Esto sugiere usar $y_{t-1}$ para explicar $y_t$ en un modelo de regresión. Usar valores previos de una serie para predecir valores actuales de la misma serie se denomina, no sorprendentemente, una autorregresión. Cuando solo se usa el pasado inmediato como predictor, utilizamos el siguiente modelo.

Definición. El modelo autorregresivo de orden uno, denotado como $AR(1)$, se escribe como \[\begin{equation} y_t = \beta_0 + \beta_1 y_{t-1} + \varepsilon_t, ~~~ t=2,\ldots,T, \tag{8.1} \end{equation}\] donde {$\varepsilon_t$} es un proceso de ruido blanco tal que $\mathrm{Cov}(\varepsilon_{t+k}, y_t)=0$ para $k>0$ y $\beta_0$ y $\beta_1$ son parámetros desconocidos.

En el modelo $AR$(1), el parámetro $\beta_0$ puede ser cualquier constante fija. Sin embargo, el parámetro $\beta_1$ está restringido a estar entre -1 y 1. Al hacer esta restricción, se puede establecer que la serie $AR$(1) {$y_t$} es estacionaria. Nota que si $\beta_1 = 1$, entonces el modelo es un paseo aleatorio y, por lo tanto, no es estacionario. Esto se debe a que, si $\beta_1 = 1$, entonces la ecuación (8.1) puede reescribirse como: \[ y_t - y_{t-1} = \beta_0 + \varepsilon_t. \] Si la diferencia de una serie forma un proceso de ruido blanco, entonces la serie misma debe ser un paseo aleatorio.

La ecuación (8.1) es útil en la discusión de propiedades del modelo. Podemos ver un modelo $AR$(1) como una generalización tanto de un proceso de ruido blanco como de un modelo de paseo aleatorio. Si $\beta_1=0$, entonces la ecuación (8.1) se reduce a un proceso de ruido blanco. Si $\beta_1 = 1$, entonces la ecuación (8.1) es un paseo aleatorio.

Un proceso estacionario donde hay una relación lineal entre $y_{t-2}$ y $y_t$ se dice autorregresivo de orden 2, y de manera similar para procesos de mayor orden. La discusión de procesos de mayor orden está en la Sección 8.5.

Selección del Modelo

Al examinar los datos, ¿cómo reconocer que un modelo autorregresivo puede ser un modelo adecuado? Primero, un modelo autorregresivo es estacionario, por lo que un gráfico de control es un buen dispositivo para examinar gráficamente los datos y buscar estabilidad. Segundo, las realizaciones adyacentes de un modelo $AR$(1) deberían estar relacionadas; esto puede detectarse visualmente con un diagrama de dispersión de valores actuales frente a valores pasados inmediatos de la serie. Tercero, podemos reconocer un modelo $AR$(1) a través de su estructura de autocorrelación, como sigue.

Una propiedad útil del modelo $AR$(1) es que la correlación entre puntos separados por $k$ unidades de tiempo resulta ser $\beta_1^{k}$. En otras palabras, \[\begin{equation} \rho_k = \mathrm{Corr}(y_t,y_{t-k}) = \frac{\mathrm{Cov}(y_t,y_{t-k})}{\sqrt{\mathrm{Var}(y_t)\mathrm{Var}(y_{t-k})}} = \frac{\mathrm{Cov}(y_t,y_{t-k})}{\sigma_y^2} = \beta_1^k. \tag{8.2} \end{equation}\]

Las primeras dos igualdades son definiciones y la tercera se debe a la estacionariedad. Al lector se le pide verificar la cuarta igualdad en los ejercicios. Por lo tanto, los valores absolutos de las autocorrelaciones de un proceso $AR$(1) se vuelven más pequeños a medida que aumenta el rezago $k$. De hecho, disminuyen a un ritmo geométrico. Observamos que para un proceso de ruido blanco, tenemos $\beta_1 = 0$, y así $\rho_k$ debería ser igual a cero para todos los rezagos $k$.

Para ayudar en la identificación del modelo, usamos la idea de igualar las autocorrelaciones observadas $r_k$ con las cantidades que esperamos de la teoría, $\rho_k$. Para ruido blanco, el coeficiente de autocorrelación muestral debería ser aproximadamente cero para cada rezago $k$. Aunque $r_k$ está algebraicamente acotado entre -1 y 1, surge la pregunta, ¿qué tan grande necesita ser $r_k$, en valor absoluto, para considerarse significativamente diferente de cero? La respuesta a este tipo de pregunta se da en términos del error estándar de la estadística. Bajo la hipótesis de no autocorrelación, una buena aproximación para el error estándar de la estadística de autocorrelación en el rezago $k$ es: \[ se(r_k) = \frac{1}{\sqrt{T}}. \] Nuestra regla práctica es que si $r_k$ supera $2 \times se(r_k)$ en valor absoluto, puede considerarse significativamente diferente de cero. Esta regla se basa en un nivel de significancia del 5%.

Ejemplo: Índice de Bonos con Inflación - Continuación. ¿Es un modelo de proceso de ruido blanco un buen candidato para representar esta serie? Las autocorrelaciones se muestran en la Tabla 8.2. Para un modelo de proceso de ruido blanco, esperamos que cada autocorrelación $r_k$ sea cercana a cero, pero notamos que, por ejemplo, $r_1=0.814$. Dado que hay $T=51$ retornos disponibles, el error estándar aproximado de cada autocorrelación es: \[ se(r_k) = \frac{1}{\sqrt{51}} = 0.140. \] Así, $r_1$ es 0.814 / 0.140 = 5.81 errores estándar por encima de cero. Usando la distribución normal como base de referencia, esta diferencia es significativa, lo que implica que un proceso de ruido blanco no es un modelo candidato adecuado.

¿Es el modelo autorregresivo de orden uno una elección adecuada? Bueno, porque $\rho_k$ = $\beta_1^{k}$, una buena estimación de $\beta_1$=$\rho_1$ es $r_1=0.814$. Si este es el caso, entonces bajo el modelo $AR$(1), otra estimación de $\rho_k$ es $(0.814)^{k}$. Así, tenemos dos estimaciones de $\rho_k$: (i) $r_k$, una estimación empírica que no depende de un modelo paramétrico y (ii) $(r_1)^{k}$, que depende del modelo $AR$(1). Para ilustrar, véase la Tabla 8.4.

Tabla 8.4. Comparación de Autocorrelaciones Empíricas con las Estimadas bajo el Modelo $AR$(1)

\[ \small{ \begin{array}{l|ccccc} \hline \text{Rezago } k & 1 & 2 & 3 & 4 & 5 \\ \hline \text{Estimado } \rho_k \text{ bajo el modelo } AR(1) & 0.814 & (0.814)^2 & (0.814)^{3} & (0.814)^{4} & (0.814)^{5} \\ & & =.66 & =.54 & =.44 & =.36 \\ \text{Autocorrelación } r_k & 0.814 & 0.632 & 0.561 & 0.447 & 0.367 \\ \hline \end{array} } \]

Dado que el error estándar aproximado es $se(r_k) = 0.14$, parece haber una buena coincidencia entre los dos conjuntos de autocorrelaciones. Debido a esta coincidencia, en la Sección 8.3 discutiremos cómo ajustar el modelo $AR$(1) a este conjunto de datos.

Proceso de Meandro

Muchos procesos muestran el patrón de que puntos adyacentes están relacionados entre sí. Pensando en un proceso que evoluciona como un río, Roberts (1991) describe gráficamente tales procesos como meandros. Para complementar esta noción intuitiva, decimos que un proceso está en meandro si la autocorrelación de rezago uno de la serie es positiva. Por ejemplo, a partir de los gráficos en las Figuras 8.1 y 8.2, parece claro que el Índice de Bonos con Inflación es un buen ejemplo de una serie en meandro. De hecho, un modelo $AR$(1) con un coeficiente de pendiente positivo es un proceso de meandro.

¿Qué sucede en el caso en que el coeficiente de pendiente se aproxima a uno, resultando en un paseo aleatorio? Considere el ejemplo de Tasas de Cambio de Hong Kong dado en el Capítulo 7. Aunque se introdujo como un modelo de tendencia cuadrática en el tiempo, un ejercicio muestra que la serie puede modelarse de manera más apropiada como un paseo aleatorio. Parece claro que cualquier punto en el proceso está altamente relacionado con cada punto adyacente en el proceso. Para enfatizar este punto, la Figura 8.3 muestra una fuerte relación lineal entre el valor actual y el valor pasado inmediato de las tasas de cambio. Debido a la fuerte relación lineal en la Figura 8.3, utilizaremos el término “proceso de meandro” para un conjunto de datos que puede modelarse utilizando un paseo aleatorio.

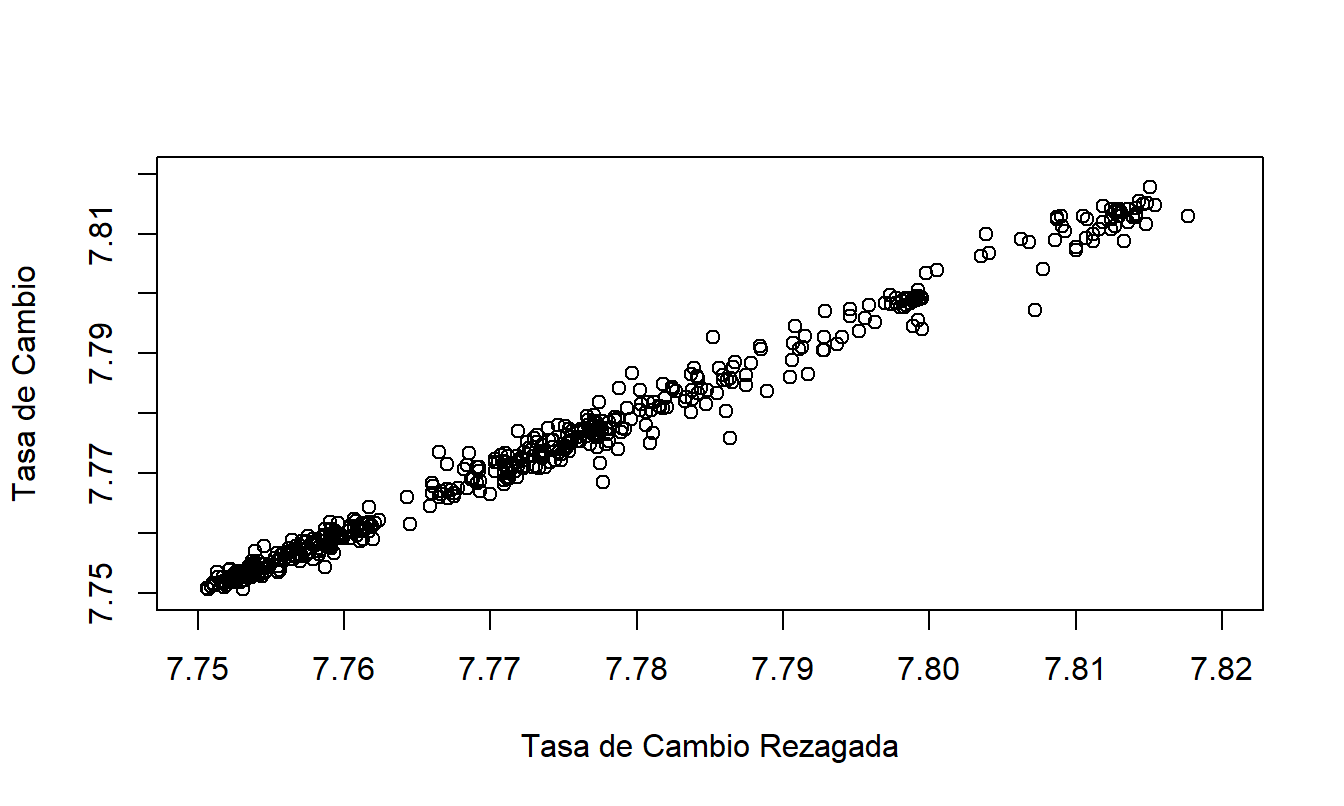
Figura 8.3: Tasas de Cambio Diarias de Hong Kong frente a Valores de Rezago.

Código R para Generar la Figura 8.3

8.3 Estimación y Verificación de Diagnóstico

Habiendo identificado un modelo tentativo, la tarea ahora es estimar los valores de $\beta_0$ y $\beta_1$. En esta sección, utilizamos el método de mínimos cuadrados condicionales para determinar las estimaciones, denotadas como $b_0$ y $b_1$, respectivamente. Este enfoque se basa en el método de mínimos cuadrados introducido en la Sección 2.1. Específicamente, ahora utilizamos los mínimos cuadrados para encontrar estimaciones que se ajusten mejor a una observación condicional a la observación previa.

Las fórmulas para las estimaciones de mínimos cuadrados condicionales se determinan a partir de los procedimientos habituales de mínimos cuadrados, utilizando el valor rezagado de $y$ como la variable explicativa. Es fácil ver que las estimaciones de mínimos cuadrados condicionales se aproximan de cerca a: \[ b_1 \approx r_1 \ \ \ \ \ \ \text{y} \ \ \ \ \ \ b_0 \approx \overline{y}(1-r_1). \] Las diferencias entre estas aproximaciones y las estimaciones de mínimos cuadrados condicionales surgen porque no tenemos una variable explicativa para $y_1$, la primera observación. Estas diferencias son típicamente pequeñas en la mayoría de las series y disminuyen a medida que aumenta la longitud de la serie.

Los residuos de un modelo $AR$(1) se definen como: \[ e_t = y_t - \left( b_0 + b_1 y_{t-1} \right). \] Como hemos visto, los patrones en los residuos pueden revelar formas de mejorar la especificación del modelo. Se puede usar un gráfico de control de los residuos para evaluar la estacionariedad y calcular la función de autocorrelación de los residuos para verificar la ausencia de patrones leves a lo largo del tiempo.

Los residuos también juegan un papel importante en la estimación de errores estándar asociados con las estimaciones de los parámetros del modelo. A partir de la ecuación (8.1), vemos que los errores no observados impulsan la actualización de las nuevas observaciones. Por lo tanto, tiene sentido centrarse en la varianza de los errores y, como en los datos transversales, definimos $\sigma^2=\sigma_{\varepsilon }^2=$ $\mathrm{Var}~\varepsilon_t.$

En la regresión transversal, debido a que las variables predictoras no eran estocásticas, la varianza de la respuesta ($\sigma_y^2$) es igual a la varianza de los errores ($\sigma^2$). Esto no es generalmente cierto en modelos de series temporales que usan predictores estocásticos. Para el modelo $AR$(1), al tomar varianzas de ambos lados de la ecuación (8.1), se establece: \[ \sigma_y^2 (1-\beta_1^2) = \sigma^2 , \] por lo que $\sigma_y^2 > \sigma^2$.

Para estimar $\sigma^2$, definimos: \[\begin{equation} s^2 = \frac{1}{T-3}\sum_{t=2}^{T} \left( e_t - \overline{e}\right)^2. \tag{8.3} \end{equation}\]

En la ecuación (8.3), el primer residuo, $e_1$, no está disponible porque $y_{t-1}$ no está disponible cuando $t=1$ y, por lo tanto, el número de residuos es $T-1$. Sin el primer residuo, el promedio de los residuos ya no es automáticamente cero y, por lo tanto, se incluye en la suma de cuadrados. Además, el denominador en el lado derecho de la ecuación (8.3) sigue siendo el número de observaciones menos el número de parámetros, teniendo en cuenta las condiciones de que el “número de observaciones” es $T-1$ y el “número de parámetros” es dos. Como en el contexto de regresión transversal, nos referimos a $s^2$ como el error cuadrático medio (MSE).

Ejemplo: Índice de Bonos de Inflación - Continuación. El índice de inflación fue ajustado utilizando un modelo $AR$(1). La ecuación estimada resulta ser: \[ \begin{array}{llllrl} \widehat{INDEX}_t & = & 0.40849 & + & 0.81384 & INDEX_{t-1} \\ {\small errores~estándar} & & {\small (0.16916)} & & {\small (0.07486)} & \end{array} \] con $s = 0.14$. Esto es menor que la desviación estándar de la serie original (0.259 de Tabla 8.1), indicando un mejor ajuste a los datos que un modelo de ruido blanco. Los errores estándar, dados entre paréntesis, fueron calculados utilizando el método de mínimos cuadrados condicionales. Por ejemplo, el $t$-ratio para $\beta_1$ es $0.8727/0.0736=14.9$, indicando que la respuesta inmediata pasada es un predictor importante de la respuesta actual.

Los residuos se calcularon como $e_t = INDEX_t - (0.2923+0.8727INDEX_{t-1})$. El gráfico de control de los residuos en la Figura 8.4 no revela patrones aparentes. Varios autocorrelaciones de residuos se presentan en Tabla 8.5. Con $T=51$ observaciones, el error estándar aproximado es $se(r_k) = 1/ \sqrt{51} = 0.14$. La autocorrelación del segundo retardo es aproximadamente -2.3 errores estándar lejos de cero, y las demás son más pequeñas, en valor absoluto. Estos valores son menores que los de Tabla 8.3, indicando que hemos eliminado algunos de los patrones temporales con la especificación $AR$(1). La autocorrelación estadísticamente significativa en el retardo 2 indica que todavía hay potencial para mejorar el modelo.

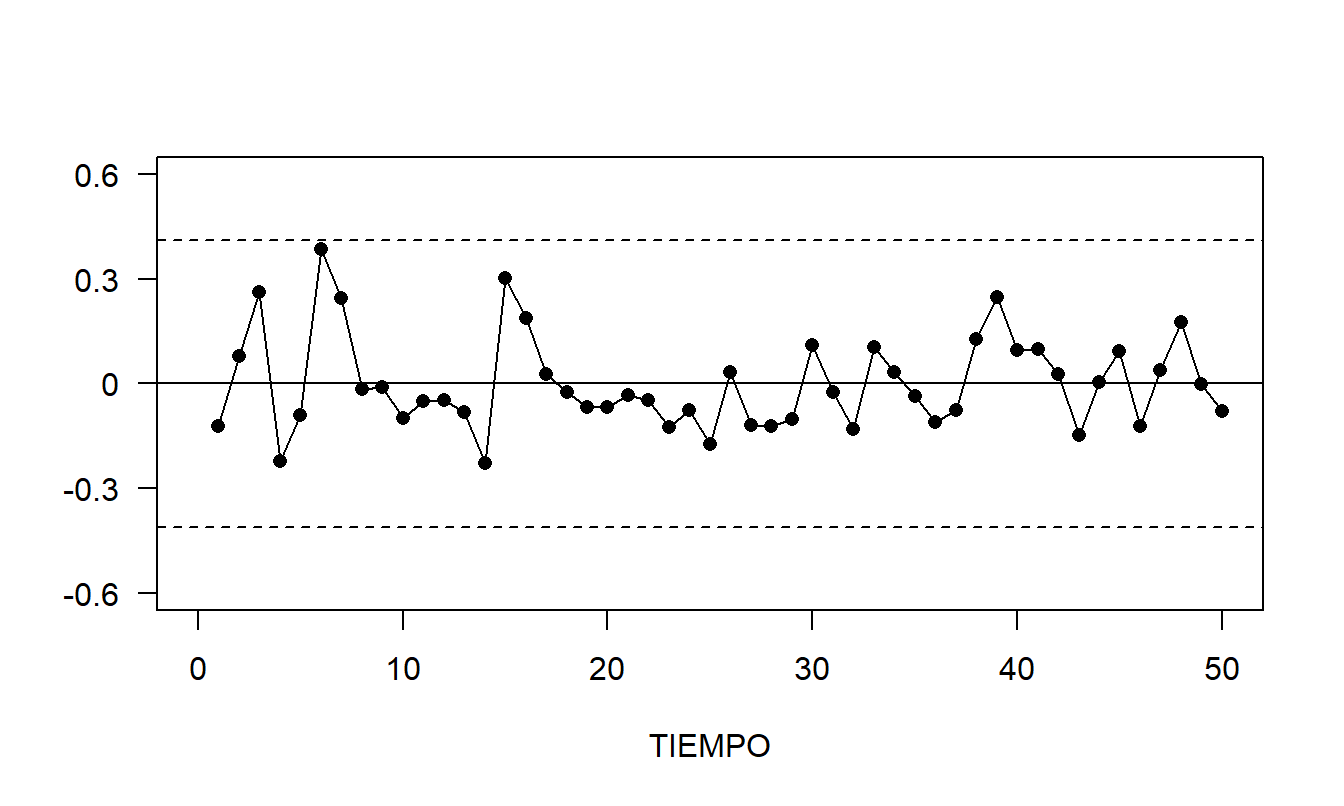
$Gráfico de Control de Residuos de un Ajuste $AR$(1) de la Serie del Índice de Inflación. Las líneas discontinuas marcan los límites de control superior e inferior, que son la media más o menos tres desviaciones estándar.$

Figura 8.4: Gráfico de Control de Residuos de un Ajuste $AR$(1) de la Serie del Índice de Inflación. Las líneas discontinuas marcan los límites de control superior e inferior, que son la media más o menos tres desviaciones estándar.

Table 8.5. Autocorrelaciones de Residuos del Modelo $AR$(1)

\[ \small{ \begin{array}{l|ccccc} \hline \text{Retardo }k & 1 & 2 & 3 & 4 & 5 \\ \hline \text{Autocorrelación de Residuos }r_k & 0.157 &-0.289 & 0.059 & 0.073& -0.124 \\ \hline \end{array} } \]

Código R para producir la Figura 8.4 y la Tabla 8.5

x
1.000
0.157
-0.289
0.059
0.073
-0.124

8.4 Suavización y Predicción

Habiendo identificado, ajustado y verificado la identificación del modelo, ahora procedemos a la inferencia básica. Recordemos que por inferencia nos referimos al proceso de utilizar el conjunto de datos para hacer afirmaciones sobre la naturaleza del mundo. Para hacer declaraciones sobre la serie, los analistas a menudo examinan los valores ajustados bajo el modelo, llamados la serie suavizada. La serie suavizada es el valor esperado estimado de la serie dado el pasado. Para el modelo $AR$(1), la serie suavizada es \[ \widehat{y}_t=b_0+b_1y_{t-1}. \]

En la Figura 8.5, un círculo abierto representa el Índice de Bonos de Inflación real y un círculo opaco representa la correspondiente serie suavizada. Debido a que la serie suavizada es la serie real con el componente de ruido estimado eliminado, a veces se interpreta como el valor “real” de la serie.

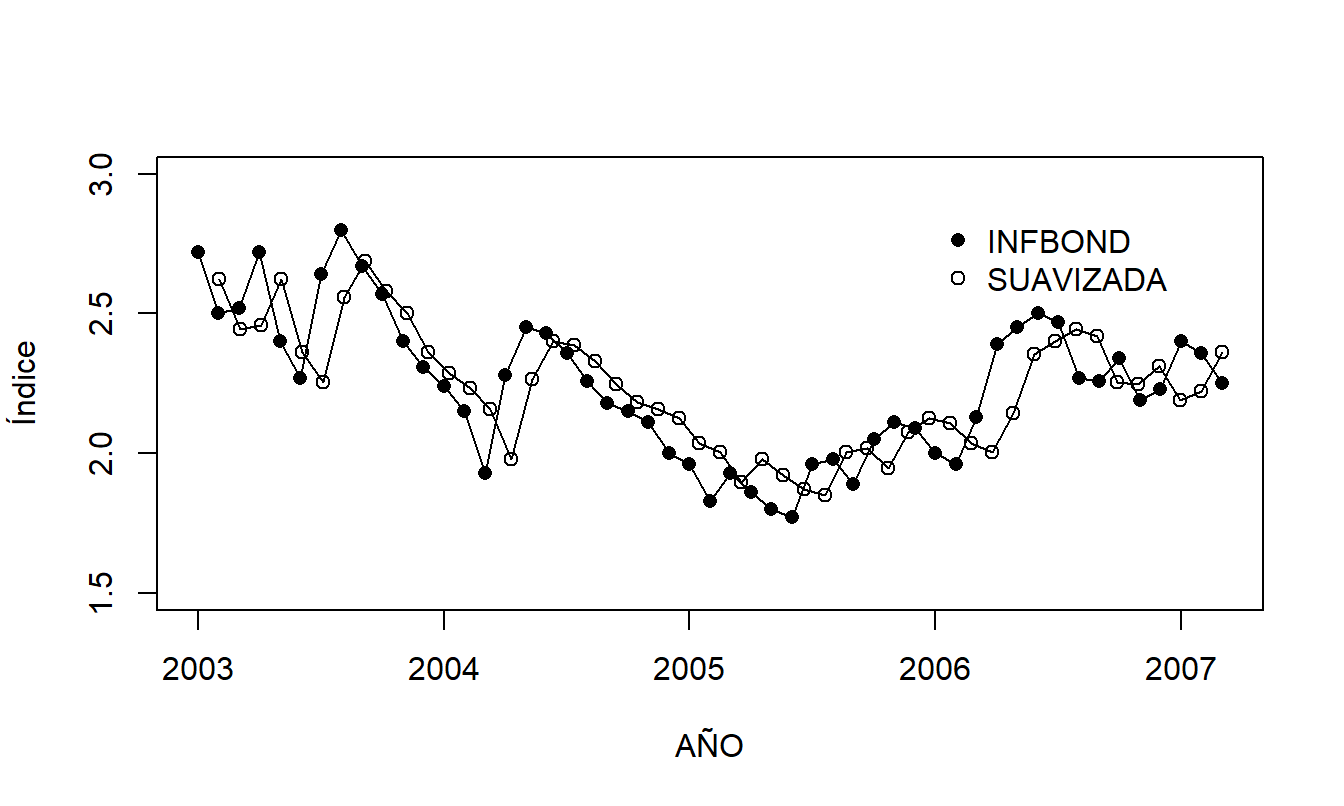
Índice de Bonos de Inflación con una Serie Suavizada Superpuesta. El índice está representado por los símbolos abiertos, la serie suavizada está representada por los símbolos opacos.

Figura 8.5: Índice de Bonos de Inflación con una Serie Suavizada Superpuesta. El índice está representado por los símbolos abiertos, la serie suavizada está representada por los símbolos opacos.

Código R para producir la Figura 8.5

Por lo general, la aplicación más importante del modelado de series de tiempo es la predicción de valores futuros de la serie. A partir de la ecuación (8.1), el valor inmediato futuro de la serie es $y_{T+1} = \beta_0 + \beta_1 y_T + \varepsilon_{T+1}$. Dado que la serie {$\varepsilon_t$} es aleatoria, una predicción natural de $\varepsilon_{T+1}$ es su media, cero. Por lo tanto, si las estimaciones $b_0$ y $b_1$ son cercanas a los verdaderos parámetros $\beta_0$ y $\beta_1$, una estimación deseable de la serie en el tiempo $T+1$ es $\widehat{y}_{T+1} = b_0 + b_1 y_T$. De manera similar, se puede calcular recursivamente una estimación para la serie $k$ puntos en el futuro, $y_{T+k}$.

Definición. El pronóstico a $k$ pasos adelante de $y_{T+k}$ para un modelo $AR$(1) se determina recursivamente como: \[\begin{equation} \widehat{y}_{T+k} = b_0 + b_1 \widehat{y}_{T+k-1}. \tag{8.4} \end{equation}\] Esto a veces se conoce como la regla de la cadena de predicción.

Para estimar el error al usar $\widehat{y}_{T+1}$ para predecir $y_{T+1}$, supongamos momentáneamente que el error al usar $b_0$ y $b_1$ para estimar $\beta_0$ y $\beta_1$ es despreciable. Bajo esta suposición, el error de pronóstico es: \[ y_{T+1}-\widehat{y}_{T+1} = \beta_0 + \beta_1 y_t + \varepsilon_{T+1} - \left( b_0 + b_1 y_t\right) \approx \varepsilon_{T+1}. \] Por lo tanto, la varianza de este error de pronóstico es aproximadamente $\sigma^2$. De manera similar, se puede demostrar que la varianza aproximada del error de pronóstico $y_{T+k}-\widehat{y}_{T+k}$ es $\sigma^2(1 + \beta_1^2 + \ldots + \beta_1^{2(k-1)})$. A partir de este cálculo de varianza y la normalidad aproximada, tenemos el siguiente intervalo de predicción.

Definición. El intervalo de predicción a $k$ pasos adelante de $y_{T+k}$ para un modelo $AR$(1) es: \[ \widehat{y}_{T+k} \pm (t\text{-valor})~s \sqrt{1 + b_1^2+ \ldots + b_1^{2(k-1)}}. \] Aquí, el $t\text{-valor}$ es un percentil de la curva $t$ usando $df=T-3$ grados de libertad. El percentil es $1 - (\text{nivel de predicción})/2$.

Por ejemplo, para intervalos de predicción al 95%, tendríamos $t\text{-valor} \approx 2$. Así, los intervalos de predicción de uno y dos pasos al 95% son: \[ \begin{array}{lc} \text{Un paso:} & \widehat{y}_{T+1}\pm \ 2s \\ \text{Dos pasos:} & \widehat{y}_{T+2}\pm \ 2s(1+b_1^2)^{1/2}. \end{array} \]

La Figura 8.6 ilustra los pronósticos del índice de bonos de inflación. Los intervalos de predicción se amplían a medida que aumenta el número de pasos en el futuro; esto refleja nuestra creciente incertidumbre al pronosticar más lejos en el tiempo.

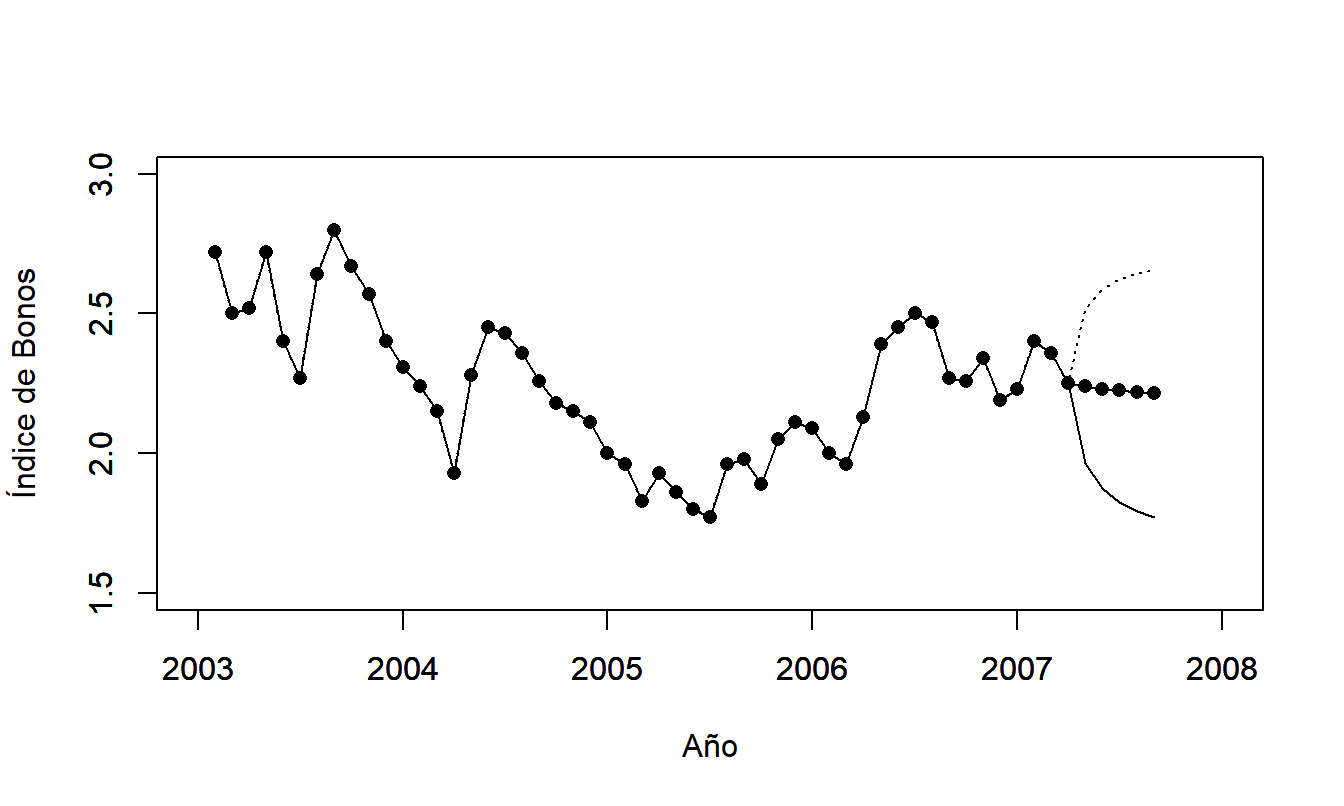
Figura 8.6: Intervalos de Predicción para la Serie de Bonos de Inflación.

Código R para producir la Figura 8.6

8.5 Modelado y Pronóstico de Box-Jenkins

Las Secciones 8.1 a 8.4 introdujeron el modelo $AR(1)$, incluyendo sus propiedades, métodos de identificación y pronóstico. Ahora introducimos una clase más amplia de modelos conocida como modelos autorregresivos integrados de promedio móvil (ARIMA), desarrollados por George Box y Gwilym Jenkins, ver Box, Jenkins y Reinsel (1994).

8.5.1 Modelos

Modelos $AR(p)$

El modelo autorregresivo de orden uno nos permite relacionar el comportamiento actual de una observación directamente con su valor inmediatamente anterior. Sin embargo, en algunas aplicaciones, también existen efectos importantes de observaciones que están más distantes en el pasado que simplemente la observación inmediata anterior. Para cuantificar esto, ya hemos introducido la autocorrelación de retardo $k$, $\rho_k$, que captura la relación lineal entre $y_t$ y $y_{t-k}$. Para incorporar esta característica en un marco de pronóstico, tenemos el modelo autorregresivo de orden p, denotado como $AR(p)$. La ecuación del modelo es: \[\begin{equation} y_t = \beta_0 + \beta_1 y_{t-1} + \ldots + \beta_p y_{t-p} + \varepsilon_t, ~~~~ t=p+1,\ldots ,T, \tag{8.5} \end{equation}\] donde {$\varepsilon_t$} es un proceso de ruido blanco tal que $\mathrm{Cov}(\varepsilon_{t+k}, y_t)=0$ para $k>0$ y $\beta_0$, $\beta_1,\ldots,\beta_p$ son parámetros desconocidos.

Por convención, cuando los analistas de datos especifican un modelo $AR(p)$, incluyen no solo $y_{t-p}$ como variable predictora, sino también los retardos intermedios $y_{t-1}, \ldots, y_{t-p+1}$. Las excepciones a esta convención son los modelos autorregresivos estacionales, que se introducirán en la Sección 9.4. También por convención, el $AR(p)$ es un modelo de un proceso estacionario y estocástico. Por lo tanto, se necesitan ciertas restricciones en los parámetros $\beta_1, \ldots, \beta_p$ para garantizar la estacionariedad (débil). Estas restricciones se desarrollan en la siguiente subsección.

Notación de Desplazamiento hacia Atrás

El operador de desplazamiento hacia atrás $\mathrm{B}$ se define como $\mathrm{B}y_t$ = $y_{t-1}$. La notación $\mathrm{B}^{k}$ significa aplicar el operador $k$ veces, es decir, \[ \mathrm{B}^{k}~y_t = \mathrm{BB \cdots B~} y_t = \mathrm{B} ^{k-1}~y_{t-1} = \cdots = y_{t-k}. \] Este operador es lineal en el sentido de que $\mathrm{B} (a_1 y_t + a_2 y_{t-1}) = a_1 y_{t-1} + a_2 y_{t-2}$, donde $a_1$ y $a_2$ son constantes. Por lo tanto, podemos expresar el modelo $AR(p)$ como: \[\begin{eqnarray*} \beta_0 + \varepsilon_t &=& y_t - \left( \beta_1 y_{t-1} + \ldots + \beta_p y_{t-p}\right) \\ &=& \left(1-\beta_1 \mathrm{B} - \ldots - \beta_p \mathrm{B}^{p}\right) y_t = \Phi \left( \mathrm{B}\right) y_t. \end{eqnarray*}\] Si $x$ es un escalar, entonces $\Phi \left( x\right) = 1 - \beta_1 x - \ldots - \beta_p x^p$ es un polinomio de orden $p$ en $x$. Por lo tanto, existen $p$ raíces de la ecuación $\Phi \left( x\right) =0$. Estas raíces, $g_1,..,g_p$, pueden o no ser números complejos. Se puede demostrar, ver Box, Jenkins y Reinsel (1994), que para la estacionariedad, todas las raíces deben estar estrictamente fuera del círculo unitario. Para ilustrar, para $p=1$, tenemos $\Phi \left( x\right) = 1 - \beta_1 x$. La raíz de esta ecuación es $g_1 = \beta_1^{-1}$. Por lo tanto, requerimos $|g_1|>1$, o $|\beta_1|<1$, para la estacionariedad.

Modelos $MA(q)$

Una interpretación del modelo $y_t=\beta_0+\varepsilon_t$ es que la perturbación $\varepsilon_t$ afecta la medida del valor “verdadero” esperado de $y_t$. De manera similar, podemos considerar el modelo $y_t=\beta_0 + \varepsilon_t-\theta_1\varepsilon_{t-1}$, donde $\theta_1 \varepsilon_{t-1}$ es la perturbación del período de tiempo anterior. Extendiéndolo, introducimos el modelo de promedio móvil de orden q, denotado como $MA(q)$. La ecuación del modelo es: \[\begin{equation} y_t = \beta_0 + \varepsilon_t - \theta_1 \varepsilon_{t-1} - \ldots - \theta_q \varepsilon_{t-q}, \tag{8.6} \end{equation}\] donde el proceso {$\varepsilon_t$} es un proceso de ruido blanco tal que $\mathrm{Cov}(\varepsilon_{t+k}, y_t)=0$ para $k>0$ y $\beta_0$, $\theta_1, \ldots, \theta_q$ son parámetros desconocidos.

Con la ecuación (8.6) es fácil ver que $\mathrm{Cov}(y_{t+k},y_t)=0$ para $k>q$. Por lo tanto, $\rho_k =0$ para $k>q$. A diferencia del modelo $AR(p)$, el proceso $MA(q)$ es estacionario para cualquier valor finito de los parámetros $\beta_0$, $\theta_1, \ldots, \theta_q$. Es conveniente escribir el $MA(q)$ usando notación de desplazamiento hacia atrás, de la siguiente manera: \[ y_t - \beta_0 = \left( 1-\theta_1\mathrm{B} - \ldots - \theta_q \mathrm{B}^q\right) \varepsilon_t = \Theta \left( \mathrm{B}\right) \varepsilon_t. \] Al igual que con $\Phi \left( x\right)$, si $x$ es un escalar, entonces $\Theta \left( x\right) = 1 - \theta_1 x - \ldots - \theta_q x^q$ es un polinomio de orden $q$ en $x$. Es desafortunado que la frase “promedio móvil” se utilice tanto para el modelo definido por la ecuación (8.6) como para el estimador definido en la Sección 9.2. Intentaremos aclarar su uso según surja.

Modelos $ARMA$ y $ARIMA$

La combinación de los modelos $AR(p)$ y $MA(q)$ da lugar al modelo autorregresivo de promedio móvil de orden $p$ y $q$, o $ARMA(p,q)$, \[\begin{equation} y_t - \beta_1 y_{t-1} - \ldots - \beta_p y_{t-p} = \beta_0 + \varepsilon _t - \theta_1 \varepsilon_{t-1} - \ldots - \theta_q \varepsilon_{t-q}, \tag{8.7} \end{equation}\] que se puede representar como \[\begin{equation} \Phi \left( \mathrm{B}\right) y_t = \beta_0 + \Theta \left( \mathrm{B} \right) \varepsilon_t. \tag{8.8} \end{equation}\]

En muchas aplicaciones, los datos requieren diferenciarse para mostrar estacionariedad. Asumimos que los datos se diferencian $d$ veces para obtener \[\begin{equation} w_t = \left( 1-\mathrm{B}\right)^d y_t = \left( 1-\mathrm{B}\right) ^{d-1}\left( y_t-y_{t-1}\right) = \left( 1-\mathrm{B}\right) ^{d-2}\left( y_t-y_{t-1}-\left( y_{t-1}-y_{t-2}\right) \right) = \ldots \tag{8.9} \end{equation}\] En la práctica, $d$ suele ser cero, uno o dos. Con esto, el modelo autorregresivo integrado de promedio móvil de orden $(p,d,q)$, denotado como $ARIMA(p,d,q)$, es \[\begin{equation} \Phi \left( \mathrm{B}\right) w_t = \beta_0+\Theta \left( \mathrm{B} \right) \varepsilon_t. \tag{8.10} \end{equation}\] A menudo, $\beta_0$ es cero para $d>0$.

Existen varios procedimientos para estimar los parámetros del modelo, incluidos la estimación de máxima verosimilitud, los mínimos cuadrados condicionales y no condicionales. En la mayoría de los casos, estos procedimientos requieren ajustes iterativos. Consulte Abraham y Ledolter (1983) para obtener más información.

Ejemplo: Pronóstico de Tasas de Mortalidad. Para cuantificar valores en seguros de vida y rentas vitalicias, los actuarios necesitan pronósticos de tasas de mortalidad específicas por edad. Desde su publicación, el método propuesto por Lee y Carter (1992) ha demostrado ser un método popular para pronosticar mortalidad. Por ejemplo, Li y Chan (2007) utilizaron estos métodos para producir pronósticos de tasas poblacionales canadienses (1921-2000) y estadounidenses (1900-2000). Mostraron cómo modificar la metodología básica para incorporar eventos atípicos, incluidas guerras y pandemias como la gripe y la neumonía.

El método de Lee-Carter suele basarse en tasas de mortalidad centrales a la edad $x$ en el tiempo $t$, denotadas por $m_{x,t}$. La ecuación del modelo es \[\begin{equation} m_{x,t} = \alpha_x + \beta_x \kappa_t + \varepsilon_{x,t} . \tag{8.11} \end{equation}\] Aquí, el intercepto ($\alpha_x$) y la pendiente ($\beta_x$) dependen únicamente de la edad $x$, no del tiempo $t$. El parámetro $\kappa_t$ captura los efectos importantes del tiempo (excepto los del término de perturbación $\varepsilon_{x,t}$).

Aunque el modelo de Lee-Carter parece a primera vista una regresión lineal con una variable explicativa, el término $\kappa_t$ no es observado y se requieren técnicas diferentes para la estimación del modelo. Existen diferentes algoritmos, incluidos la descomposición en valores singulares propuesta por Lee y Carter, el enfoque de componentes principales y un modelo de regresión de Poisson; ver Li y Chan (2007) para referencias.

El término $\kappa_t$ variable en el tiempo se representa típicamente usando un modelo $ARIMA$. Li y Chan encontraron que un paseo aleatorio (con ajustes para eventos inusuales) era un modelo adecuado para las tasas de Canadá y EE.UU. (con coeficientes diferentes), reforzando los hallazgos de Lee y Carter.

8.5.2 Pronóstico

Pronósticos Puntuales Óptimos

De manera similar a los pronósticos introducidos en la Sección 8.4, es común proporcionar pronósticos que son estimaciones de expectativas condicionales de la distribución predictiva. Específicamente, asumimos que tenemos disponible una realización de {$y_1, y_2, \ldots, y_T$} y deseamos pronosticar $y_{T+l}$, el valor de la serie “$l$” pasos hacia adelante en el futuro. Si los parámetros del proceso fueran conocidos, entonces usaríamos $\mathrm{E}(y_{T+l}|y_T,y_{T-1},y_{T-2},\ldots)$, es decir, la expectativa condicional de $y_{T+l}$ dado el valor de la serie hasta el tiempo $T$. Usamos la notación $\mathrm{E}_T$ para esta expectativa condicional.

Para ilustrar, tomando $t=T+l$ y aplicando $\mathrm{E}_T$ a ambos lados de la ecuación (8.7), obtenemos \[\begin{equation} y_T(l) - \beta_1 y_T(l-1) - \ldots - \beta_p y_T(l-p) = \beta_0 + \mathrm{E}_T\left( \varepsilon_{T+l} - \theta_1 \varepsilon_{T+l-1} - \ldots - \theta _q \varepsilon_{T+l-q}\right) , \tag{8.12} \end{equation}\] usando la notación $y_T(k) = \mathrm{E}_T\left( y_{T+k}\right)$. Para $k \leq 0$, $\mathrm{E}_T\left( y_{T+k}\right) =y_{T+k}$, ya que el valor de $y_{T+k}$ es conocido en el tiempo $T$. Además, $\mathrm{E}_T\left( \varepsilon_{T+k}\right) =0$ para $k>0$ ya que los términos de perturbación en el futuro se asumen no correlacionados con los valores actuales y pasados de la serie. Por lo tanto, la ecuación (8.12) proporciona la base de la regla en cadena de pronóstico, donde proporcionamos recursivamente pronósticos en el tiempo $l$ basados en pronósticos y realizaciones previas de la serie. Para implementar la ecuación (8.12), sustituimos estimaciones de parámetros y residuales por los términos de perturbación.

Caso Especial - Modelo MA(1). Ya hemos visto la regla en cadena de pronóstico para el modelo $AR(1)$ en la Sección 8.4. Para el modelo $MA(1)$, note que para $l\geq 2$, tenemos $y_T(l)=\mathrm{E}_T\left( y_{T+l}\right)$ $=\mathrm{E}_T\left( \beta_0+\varepsilon_{T+l}-\theta_1\varepsilon_{T+l-1}\right) =\beta_0$, porque $\varepsilon_{T+l}$ y $\varepsilon _{T+l-1}$ están en el futuro en el tiempo $T$. Para $l=1$, tenemos $y_T(1)= \mathrm{E}_T\left( \beta_0+\varepsilon_{T+1}-\theta _1\varepsilon_T\right)$ $=\beta_0-\theta_1\mathrm{E}_T\left( \varepsilon_T\right)$. Típicamente, uno estimaría el término $\mathrm{E}_T\left( \varepsilon_T\right)$ usando el residual en el tiempo $T$.

Representación del Coeficiente $\psi$

Cualquier modelo $ARIMA(p,d,q)$ puede expresarse como \[ y_t=\beta_0^{\ast }+\varepsilon_t+\psi_1 \varepsilon_{t-1}+\psi _2\varepsilon_{t-2}+\ldots=\beta_0^{\ast }+\sum_{k=0}^{\infty }\psi _{k}\varepsilon_{t-k}, \] llamado la representación del coeficiente $\psi$. Es decir, el valor actual de un proceso puede expresarse como una constante más una combinación lineal de las perturbaciones actuales y pasadas. Los valores de {$\psi_{k}$} dependen de los parámetros lineales del proceso $ARIMA$ y pueden determinarse mediante una sustitución recursiva sencilla. Para ilustrar, para el modelo $AR(1)$, tenemos \[\begin{eqnarray*} y_t &=&\beta_0+\varepsilon_t+\beta_1y_{t-1}=\beta_0+\varepsilon _t+\beta_1\left( \beta_0+\varepsilon _{t-1}+\beta_1y_{t-2}\right) =\ldots \\ &=&\frac{\beta_0}{1-\beta_1}+\varepsilon_t+\beta_1\varepsilon _{t-1}+\beta_1^2\varepsilon_{t-2}+\ldots=\frac{\beta_0}{1-\beta_1} +\sum_{k=0}^{\infty }\beta_1^{k}\varepsilon_{t-k}. \end{eqnarray*}\] Es decir, $\psi_{k}=\beta_1^{k}$.

Intervalo de Pronóstico

Usando la representación del coeficiente $\psi$, podemos expresar la expectativa condicional de $y_{T+l}$ como \[ \mathrm{E}_T\left( y_{T+l}\right) =\beta_0^{\ast }+\sum_{k=0}^{\infty }\psi_{k}\mathrm{E}_T\left( \varepsilon _{T+l-k}\right) =\beta_0^{\ast }+\sum_{k=l}^{\infty }\psi _{k}\mathrm{E}_T\left( \varepsilon_{T+l-k}\right) . \] Esto se debe a que, en el tiempo $T$, los errores $\varepsilon_T,\varepsilon _{T-1},\ldots$, han sido determinados por la realización del proceso. Sin embargo, los errores $\varepsilon_{T+1},\ldots,\varepsilon_{T+l}$ no se han realizado y, por lo tanto, tienen una expectativa condicional igual a cero. Así, el error de pronóstico de $l$ pasos es \[ y_{T+l}-\mathrm{E}_T\left( y_{T+l}\right) =\beta_0^{\ast }+\sum_{k=0}^{\infty }\psi_{k}\varepsilon_{T+l-k}-\left( \beta_0^{\ast }+\sum_{k=l}^{\infty }\psi_{k}\mathrm{E}_T\left( \varepsilon _{T+l-k}\right) \right) =\sum_{k=0}^{l-1}\psi_{k}\varepsilon _{T+l-k}. \]

Nos centramos en la variabilidad de los errores de los pronósticos. Es decir, cálculos sencillos arrojan $\mathrm{Var}\left( y_{T+l}-\mathrm{E}_T \left( y_{T+l}\right) \right) =\sigma^2\sum_{k=1}^{l-1}\psi_{k}^2$. Así, asumiendo normalidad en los errores, un intervalo de pronóstico de $100(1-\alpha)$ para $y_{T+l}$ es \[ \widehat{y}_{T+l} \pm (t-value) s \sqrt{\sum_{k=0}^{l-1} \widehat{\psi}_k^2} . \] donde $t$-value es el percentil $(1-\alpha /2)$ de una $t$-distribución con $df=T-(número~de~parámetros~lineales)$. Si $y_t$ es un proceso $ARIMA(p,d,q)$, entonces $\psi_{k}$ es una función de $\beta_1,\ldots,\beta_p,\theta_1,\ldots,\theta_q$ y el número de parámetros lineales es $1+p+q$.

8.6 Aplicación: Tasas de Cambio de Hong Kong

La Sección 7.2 presentó la serie de Tasas de Cambio de Hong Kong, basada en $T=502$ observaciones diarias para el período del 1 de abril de 2005 al 31 de mayo de 2007. Se ajustó una tendencia cuadrática al modelo que produjo un $R^2=86.2$ con una desviación estándar residual de $s=0.0068$. Ahora mostramos cómo mejorar este ajuste utilizando modelos $ARIMA$.

Para comenzar, la Figura 8.7 muestra un gráfico de series de tiempo de los residuos del modelo de tendencia cuadrática en el tiempo. Este gráfico muestra un patrón serpenteante, lo que sugiere que hay información en los residuos que puede ser explotada.

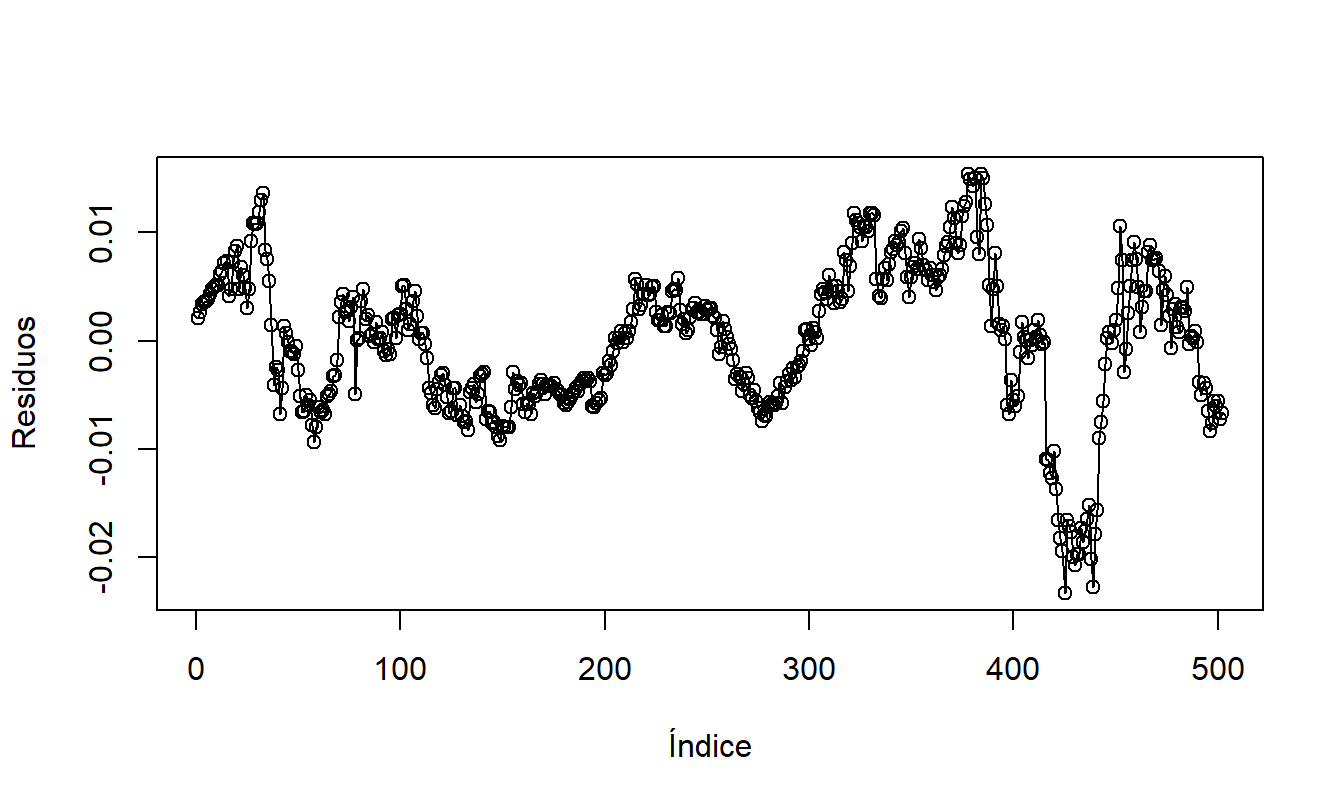
Figura 8.7: Residuos de un Modelo de Tendencia Cuadrática en el Tiempo de las Tasas de Cambio de Hong Kong.

R Code to Produce Figure 8.7

Más evidencia de estos patrones se encuentra en la tabla de autocorrelaciones en Tabla 8.6. Aquí observamos grandes autocorrelaciones residuales que no disminuyen rápidamente a medida que el retraso $k$ aumenta. Un patrón similar también es evidente en la serie original, EXHKUS. Esto confirma la no estacionariedad que observamos en la Sección 7.2.

Como una transformación alternativa, se diferenciaron las series, produciendo DIFFHKUS. Esta serie diferenciada tiene una desviación estándar de $s_{DIFF}=0.0020$, lo que sugiere que es más estable que la serie original o los residuos del modelo de tendencia cuadrática en el tiempo. Tabla 8.6 presenta las autocorrelaciones de la serie diferenciada, indicando patrones leves. Sin embargo, estas autocorrelaciones todavía son significativamente diferentes de cero. Para $T=501$ diferencias, podemos usar como un error estándar aproximado para las autocorrelaciones $1/\sqrt{501}\approx 0.0447.$ Con esto, vemos que la autocorrelación en el retraso 2 es $0.151/0.0447\approx 3.38$ errores estándar por debajo de cero, lo cual es estadísticamente significativo. Esto sugiere introducir otro modelo para aprovechar la información en los patrones de series de tiempo.

Tabla 8.6. Autocorrelaciones de las Tasas de Cambio de Hong Kong

\[ \small{ \begin{array}{l|cccccccccc} \hline \text{Retraso }& 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline \text{Residuos del} & 0.958 & 0.910 & 0.876 & 0.847 & 0.819 & 0.783 & 0.748 & 0.711 & 0.677 & 0.636 \\ \ \ \text{Modelo Cuadrático} & & & & & & & & & & \\ \text{EXHKUS} & 0.988 & 0.975 & 0.963 & 0.952 & 0.942 & 0.930 & 0.919 & 0.907 & 0.895 & 0.882 \\ \ \ \text{(Serie Original)} & & & & & & & & & & \\ \text{DIFFHKUS} & 0.078 & -0.151 & -0.038 & -0.001 & 0.095 & -0.005 & 0.051 & -0.012 & 0.084 & -0.001 \\ \hline \end{array} } \]

R Code to Produce Table 8.6

Selección de Modelo y Autocorrelaciones Parciales

Para todos los modelos autorregresivos estacionarios, se puede demostrar que los valores absolutos de las autocorrelaciones disminuyen a medida que el retraso $k$ aumenta. En el caso de que las autocorrelaciones disminuyan aproximadamente como una serie geométrica, se puede identificar un modelo $AR(1)$. Desafortunadamente, para otros tipos de series autorregresivas, las reglas prácticas para identificar la serie a partir de las autocorrelaciones se vuelven más confusas. Un dispositivo útil para identificar el orden de una serie autorregresiva es la función de autocorrelación parcial.

Al igual que las autocorrelaciones, ahora definimos una autocorrelación parcial en un retraso específico $k$. Consideremos la ecuación del modelo \[ y_t=\beta_{0,k}+\beta_{1,k} y_{t-1}+\ldots+\beta_{k,k} y_{t-k} + \varepsilon_t. \] Aquí, {$\varepsilon_t$} es un error estacionario que puede o no ser un proceso de ruido blanco. El segundo subíndice en los $\beta$, “$,k$”, está allí para recordarnos que el valor de cada $\beta$ puede cambiar cuando cambia el orden del modelo, $k$. Con esta especificación del modelo, podemos interpretar $\beta_{k,k}$ como la correlación entre $y_t$ y $y_{t-k}$ después de haber eliminado los efectos de las variables intermedias, $y_{t-1},\ldots,y_{t-k+1}$. Esta es la misma idea que el coeficiente de correlación parcial, introducido en la Sección 4.4. Las estimaciones de los coeficientes de correlación parcial, $b_{k,k}$, pueden calcularse utilizando mínimos cuadrados condicionales u otras técnicas. Al igual que con otras correlaciones, podemos usar $1/\sqrt{T}$ como un error estándar aproximado para detectar diferencias significativas con respecto a cero.

Las autocorrelaciones parciales se utilizan en la identificación de modelos de la siguiente manera. Primero calcule las primeras estimaciones, $b_{1,1},b_{2,2},b_{3,3}$, y así sucesivamente. Luego, elija el orden del modelo autorregresivo como el mayor $k$ de modo que la estimación $b_{k,k}$ sea significativamente diferente de cero.

Para ver cómo se aplica esto en el ejemplo de la Tasa de Cambio de Hong Kong, recordemos que el error estándar aproximado para las correlaciones es $1/\sqrt{501}\approx 0.0447$. Tabla 8.7 proporciona las primeras diez autocorrelaciones parciales para las tasas y para sus diferencias. Usando el doble del error estándar como nuestra regla de corte, vemos que la segunda autocorrelación parcial de las diferencias excede $2\times 0.0447=0.0894$ en valor absoluto. Esto sugeriría usar un $AR(2)$ como una primera elección de modelo tentativa. Alternativamente, el lector puede argumentar que, dado que las autocorrelaciones parciales quinta y novena también son estadísticamente significativas, un $AR(5)$ o $AR(9)$ más complejo podría ser más apropiado. La filosofía es “usar el modelo más simple posible, pero no más simple”. Preferimos emplear modelos más simples y ajustarlos primero, luego probar si capturan o no los aspectos importantes de los datos.

Finalmente, puede estar interesado en ver qué sucede con las autocorrelaciones parciales calculadas en una serie no estacionaria. Tabla 8.7 proporciona autocorrelaciones parciales para la serie original (EXHKUS). Observe cuán grande es la primera autocorrelación parcial. Es decir, otra forma de identificar una serie como no estacionaria es examinar la función de autocorrelación parcial y buscar una gran autocorrelación parcial en el primer retraso.

Tabla 8.7. Autocorrelaciones Parciales de EXHKUS y DIFFHKUS

\[ \small{ \begin{array}{l|cccccccccc} \hline \text{Retraso} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline \text{EXHKUS} & 0.988 & -0.034 & 0.051 & 0.019 & -0.001 & -0.023 & 0.010 & -0.047 & -0.013 & -0.049 \\ \text{DIFFHKUS} & 0.078 & -0.158 & -0.013 & -0.021 & 0.092 & -0.026 & 0.085 & -0.027 & 0.117 & -0.036 \\ \hline \end{array} } \]

R Code to Produce Table 8.7

Verificación de Residuos

Después de identificar y ajustar un modelo, la verificación de residuos sigue siendo una parte importante para determinar la validez del modelo. Para el modelo $ARMA(p,q)$, calculamos los valores ajustados como

\[\begin{equation} \widehat{y}_t = b_0 + b_1 y_{t-1} + \ldots + b_p y_{t-p} - \widehat{\theta}_1 e_{t-1}- \ldots - \widehat{\theta }_q e_{t-q}. \tag{8.13} \end{equation}\] Aquí, $\widehat{\theta}_1, \ldots, \widehat{\theta}_q$ son estimaciones de $\theta_1,\ldots, \theta_q$. Los residuos pueden calcularse de la manera habitual, es decir, como $e_t=y_t-\widehat{y}_t$. Sin más aproximaciones, observe que los residuos iniciales faltan porque los valores ajustados antes del tiempo $t=\max (p,q)$ no pueden calcularse usando la ecuación (8.13). Para verificar patrones, use los dispositivos descritos en la Sección 8.3, como el gráfico de control para verificar la estacionariedad y la función de autocorrelación para verificar las relaciones entre variables con retrasos.

Autocorrelación de Residuos

Los residuos del modelo ajustado deberían parecerse a un ruido blanco y, por lo tanto, mostrar pocos patrones discernibles. En particular, esperamos que $r_k(e)$, la autocorrelación de los residuos en el retraso $k$, sea aproximadamente cero. Para evaluar esto, tenemos que $se\left( r_k(e) \right) \approx 1/\sqrt{T}$. Más precisamente, MacLeod (1977, 1978) ha dado aproximaciones para una amplia clase de modelos $ARMA$. Resulta que el $1/\sqrt{T}$ puede mejorarse para valores pequeños de $k$. (Estos valores mejorados pueden verse en la salida de la mayoría de los paquetes estadísticos). La mejora depende del modelo que se esté ajustando. Para ilustrar, supongamos que un modelo $AR(1)$ con parámetro autorregresivo $\beta_1$ se ajusta a los datos. Entonces, el error estándar aproximado de la autocorrelación residual en el retraso uno es $|\beta_1|/\sqrt{T}$. Este error estándar puede ser mucho menor que $1/\sqrt{T}$, dependiendo del valor de $\beta_1$.

Prueba de Varios Retrasos

Para probar si hay autocorrelación residual significativa en un retraso específico $k$, usamos $r_k(e) /se\left( r_k(e) \right)$. Además, para verificar si los residuos se parecen a un proceso de ruido blanco, podemos probar si $r_k(e)$ está cerca de cero para varios valores de $k$. Para probar si las primeras $K$ autocorrelaciones residuales son cero, se utiliza la estadística chi-cuadrado de Box y Pierce (1970) \[ Q_{BP} = T \sum_{k=1}^{K} r_k \left( e \right)^2. \] Aquí, $K$ es un número entero especificado por el usuario. Si no hay autocorrelación real, esperamos que $Q_{BP}$ sea pequeño; más precisamente, Box y Pierce demostraron que $Q_{BP}$ sigue una distribución aproximada $\chi^2$ con $df=K-(número~de~parámetros~lineales)$. Para un modelo $ARMA(p,q)$, el número de parámetros lineales es $1+p+q$. Otra estadística ampliamente utilizada es \[ Q_{LB}=T(T+2)\sum_{k=1}^{K}\frac{r_k \left( e\right)^2}{T-k}. \]

debido a Ljung y Box (1978). Esta estadística tiene un mejor rendimiento en muestras pequeñas que la estadística $BP$. Bajo la hipótesis de no autocorrelación residual, $Q_{LB}$ sigue la misma distribución $\chi^2$ que $Q_{BP}$. Así, para cada estadística, rechazamos $H_{0}$: No hay autocorrelación residual si la estadística excede el valor $\chi$, un percentil $1-\alpha$ de una distribución $\chi^2$. Una regla práctica conveniente es usar $\chi$-valor = 1.5 $df$.

Ejemplo: Tasa de Cambio de Hong Kong - Continuación. Se ajustaron dos modelos, el $ARIMA(2,1,0)$ y el $ARIMA(0,1,2)$; estos son los modelos $AR(2)$ y $MA(2)$ después de tomar diferencias. Usando {$y_t$} para las diferencias, el modelo $AR(2)$ estimado es: \[ \begin{array}{clllrllll} \widehat{y}_t & = & 0.0000317 & + & 0.0900 & y_{t-1} & - & 0.158 & y_{t-2} \\ {\small t-estadística} & & {\small [0.37]} & & {\small [2.03]} & & & {\small [-3.57]} & \end{array} \] con un error estándar residual de $s=0.00193.$ El modelo $MA(2)$ estimado es: \[ \begin{array}{clllrllll} \widehat{y}_t & = & 0.0000297 & - & 0.0920 & e_{t-1} & + & 0.162 & e_{t-2} \\ {\small t-estadística} & & {\small [0.37]} & & {\small [-2.08]} & & & {\small [3.66]} & \end{array} \] con el mismo error estándar residual de $s=0.00193.$ Estas estadísticas indican que los modelos son aproximadamente comparables. La estadística de Ljung-Box en Tabla 8.8 también indica una gran similitud entre los modelos.

Tabla 8.8. Estadísticas de Ljung-Box $Q_{LB}$ para los Modelos de Tasa de Cambio de Hong Kong

\[ \small{ \begin{array}{l|ccccc} \hline &&& \text{Retraso }K \\ \text{Modelo} & 2 & 4 & 6 & 8 & 10 \\ \hline AR(2) & 0.0065 & 0.5674 & 6.3496 & 10.4539 & 16.3258 \\ MA(2) & 0.0110 & 0.2872 & 6.6557 & 11.3361 & 17.6882 \\ \hline \end{array} } \]

R Code to Produce Table 8.8

	Retraso 2	Retraso 4	Retraso 6	Retraso 8	Retraso 10
AR(2)	0.0065	0.5674	6.3496	10.4539	16.3258
MA(2)	0.0110	0.2872	6.6557	11.3361	17.6882

Los modelos ajustados $MA$(2) y $AR$(2) son aproximadamente similares. Presentamos el modelo $AR$(2) solo para fines de predicción porque los modelos autorregresivos suelen ser más fáciles de interpretar. La Figura 8.8 resume las predicciones, calculadas para diez días. Note los intervalos de predicción que se amplían, algo típico en pronósticos para series no estacionarias.

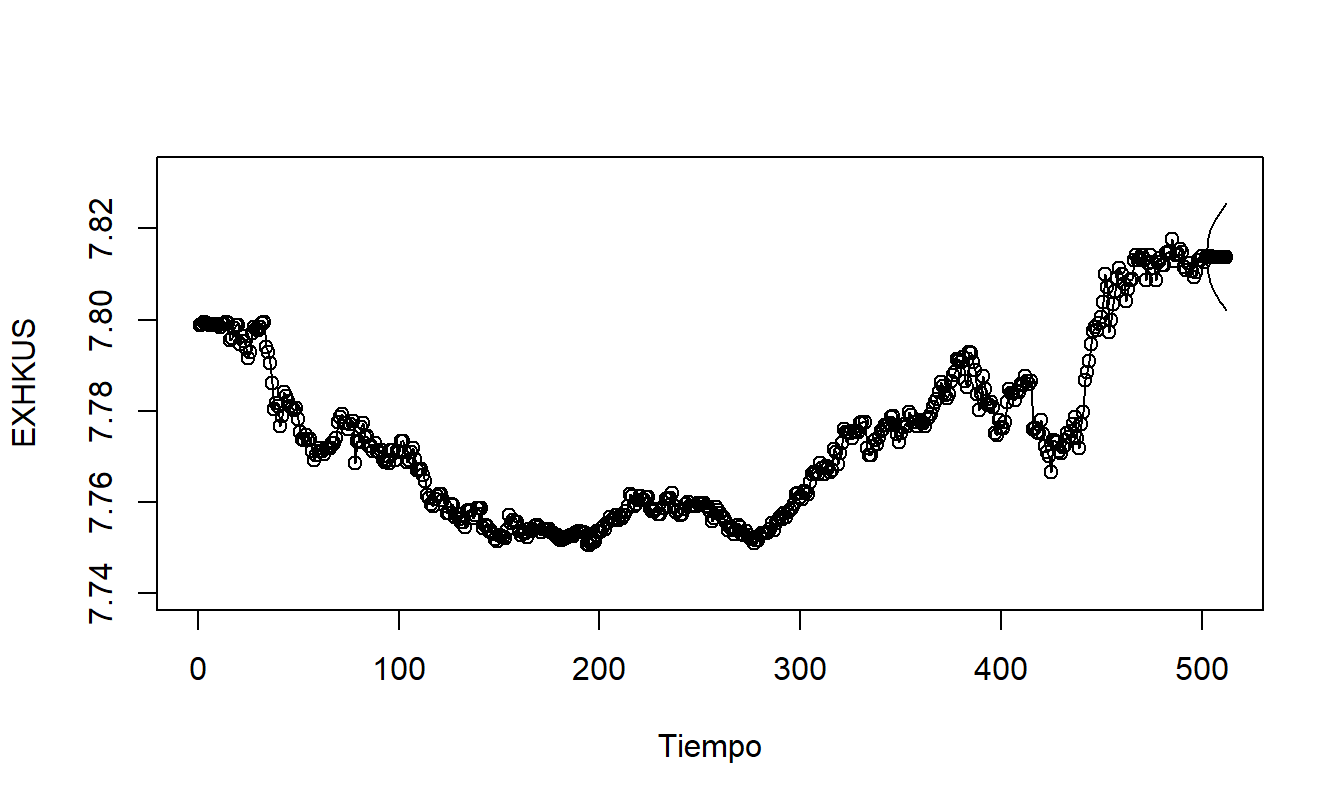
$Pronósticos a Diez Días e Intervalos de Predicción de las Tasas de Cambio de Hong Kong. Los pronósticos se basan en el modelo $ARIMA(2,1,0)$.$

Figura 8.8: Pronósticos a Diez Días e Intervalos de Predicción de las Tasas de Cambio de Hong Kong. Los pronósticos se basan en el modelo $ARIMA(2,1,0)$.

R Code to Produce Figure 8.8

8.7 Lecturas Adicionales y Referencias

El libro clásico introductorio a las series temporales de Box-Jenkins es Box, Jenkins y Reinsel (1994).

Referencias del Capítulo

Abraham, Bovas and Johannes Ledolter (1983). Statistical Methods for Forecasting. John Wiley & Sons, New York.
Box, George E. P., Gwilym M. Jenkins and Gregory C. Reinsel (1994). Time Series Analysis: Forecasting and Control, Third Edition, Prentice-Hall, Englewood Cliffs, New Jersey.
Box, George E. P., and D. A. Pierce (1970). Distribution of residual autocorrelations in autoregressive moving average time series models. Journal of the American Statistical Association 65, 1509-1526.
Chan, Wai-Sum and Siu-Hang Li (2007). The Lee-Carter model for forecasting mortality, revisited. North American Actuarial Journal 11(1), 68-89.
Lee, Ronald D. and Lawrence R. Carter (1992). Modelling and forecasting U.S. mortality. Journal of the American Statistical Association 87, 659-671.
Ljung, G. M. and George E. P. Box (1978). On a measure of lack of fit in time series models. Biometrika 65, 297-303.
MacLeod, A. I. (1977). Improved Box-Jenkins estimators. Biometrika 64, 531-534.
MacLeod, A. I. (1978). On the distribution of residual autocorrelations in Box-Jenkins models. Journal of the Royal Statistical Society B 40, 296-302.
Miller, Robert B. and Dean W. Wichern (1977). Intermediate Business Statistics: Analysis of Variance, Regression and Time Series. Holt, Rinehart and Winston, New York.
Roberts, Harry V. (1991). Data Analysis for Managers with MINITAB. Scientific Press, South San Francisco, CA.

8.1. Un fondo mutuo ha proporcionado tasas de rendimiento de inversión durante cinco años consecutivos como sigue:

\[ \begin{array}{l|ccccc} \hline \text{Año} & 1 & 2 & 3 & 4 & 5 \\ \hline \text{Rendimiento} & 0.09 & 0.08 & 0.09 & 0.12 & -0.03 \\ \hline \end{array} \]

Determine $r_1$ y $r_2$, los coeficientes de autocorrelación para retrasos 1 y 2.

8.2. La estadística Durbin-Watson está diseñada para detectar autocorrelación y se define como: \[ DW = \frac {\sum_{t=2}^T (y_t - y_{t-1})^2} {\sum_{t=1}^T (y_t - \bar{y})^2}. \]

Derive la relación aproximada entre $DW$ y el coeficiente de autocorrelación de retraso 1, $r_1$.
Suponga que $r_1 = 0.4$. ¿Cuál es el valor aproximado de $DW$?

8.3. Considere las fórmulas del modelo de regresión lineal del Capítulo 2 con $y_{t-1}$ en lugar de $x_t$, para $t=2, \ldots, T$.

Proporcione una expresión exacta para $b_1$.
Proporcione una expresión exacta para $b_0$.
Demuestre que $b_0 \approx \bar{y} (1-r_1)$.

8.4. Comience con el modelo $AR$(1) como en la ecuación (8.1).

Tome las varianzas de cada lado de la ecuación (8.1) para mostrar que $\sigma_y^2(1-\beta_1^2) = \sigma^2,$ donde $\sigma_y^2 = \mathrm{Var}~y_t$ y $\sigma^2 = \mathrm{Var}~\varepsilon_t$.
Demuestre que $\mathrm{Cov}(y_t,y_{t-1}) = \beta_1 \sigma_y^2.$
Demuestre que $\mathrm{Cov}(y_t,y_{t-k}) = \beta_1^k \sigma_y^2.$
Use la parte (c) para establecer la ecuación (8.2).

8.5. Considere pronósticos con el modelo $AR$(1).

Use la regla de encadenamiento de pronósticos en la ecuación (8.4) para mostrar \[ y_{T+k}-\widehat{y}_{T+k} \approx \varepsilon_{T+k} + \beta_1 \varepsilon_{T+k-1} + \cdots + \beta_1^{k-1} \varepsilon_{T+1}. \]
A partir de la parte (a), demuestre que la varianza aproximada del error de pronóstico es $\sigma^2 \sum_{l=0}^{k-1} \beta_1^{2l}.$

8.6. Estos datos consisten en los 503 rendimientos diarios de los años calendario 2005 y 2006 del índice ponderado por valor del Standard and Poor’s (S&P). (El archivo de datos contiene años adicionales; este ejercicio usa solo los datos de 2005 y 2006). Cada año, hay alrededor de 250 días en los que el mercado está abierto y se intercambian acciones; los fines de semana y festivos está cerrado. Hay varios índices para medir el rendimiento general del mercado. El índice ponderado por valor se crea suponiendo que la cantidad invertida en cada acción es proporcional a su capitalización de mercado. Aquí, la capitalización de mercado es simplemente el precio inicial por acción multiplicado por el número de acciones en circulación. Una alternativa es el índice ponderado por igual, creado tomando un promedio simple del precio de cierre o último precio de las acciones que forman parte del S&P en ese día de negociación.

La teoría económica financiera establece que si el mercado fuera predecible, muchos inversionistas intentarían aprovechar estas predicciones, forzando así la imprevisibilidad. Por ejemplo, supongamos que un modelo estadístico predice de manera confiable que el fondo mutuo A se duplicará en los próximos 18 meses. Entonces, el principio de no arbitraje en economía financiera establece que varios inversionistas alerta, armados con la información del modelo estadístico, ofertarían para comprar el fondo mutuo A, lo que provocaría un aumento en el precio debido al aumento de la demanda. Estos inversionistas alerta continuarían comprando hasta que el precio del fondo mutuo A aumentara al punto donde el rendimiento fuera equivalente a otras oportunidades de inversión en la misma clase de riesgo. Así, cualquier ventaja producida por el modelo estadístico desaparecería rápidamente, eliminando esta ventaja.

Por lo tanto, la teoría económica financiera establece que para mercados líquidos como las acciones representadas en el índice S&P no deberían detectarse patrones, resultando en un proceso de ruido blanco. En la práctica, se ha encontrado que los costos de compra y venta de acciones (llamados costos de transacción) son lo suficientemente altos como para evitar que aprovechemos estas ligeras tendencias en las fluctuaciones del mercado. Esto ilustra un punto conocido como estadísticamente significativo pero no prácticamente importante. Esto no sugiere que la estadística no sea práctica (¡ni pensarlo!). En cambio, la estadística en sí misma no reconoce explícitamente factores, como los económicos, psicológicos y otros, que pueden ser extremadamente importantes en una situación dada. Corresponde al analista interpretar el análisis estadístico a la luz de estos factores.

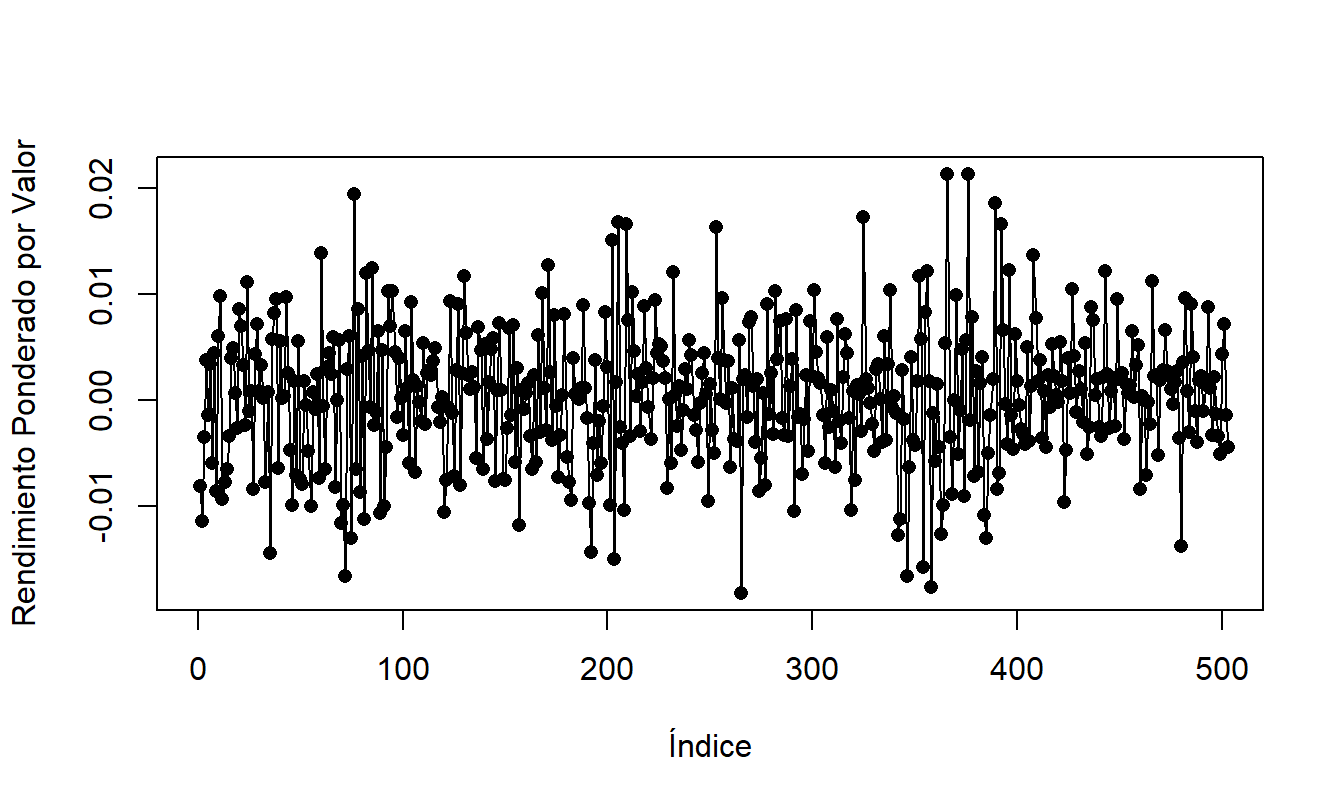
Figura 8.9: Gráfico de Serie Temporal del Rendimiento Diario del Mercado S & P, 2005-2006.

R Code to Produce Figure 8.9

El gráfico de la serie temporal en la Figura 8.9 da una idea preliminar de las características de la secuencia. Comente sobre la estacionariedad de la secuencia.
Calcule estadísticas resumidas de la secuencia. Suponga que asume un modelo de ruido blanco para la secuencia. Calcule pronósticos de 1, 2 y 3 pasos para los rendimientos diarios de los tres primeros días de negociación de 2007.
Calcule las autocorrelaciones para los retrasos 1 a 10. ¿Detecta alguna autocorrelación que sea estadísticamente significativa y diferente de cero?

Modelado de Regresión con Aplicaciones Actuariales y Financieras