Capítulo 20 Redacción de Informes: Comunicando Resultados del Análisis de Datos | Modelado de Regresión con Aplicaciones Actuariales y Financieras

20.1 Visión General

Se ha explorado la última relación, se ha estimado el último parámetro, se ha realizado el último pronóstico, y ahora estás listo para compartir los resultados de tu análisis estadístico con el mundo. El medio de comunicación puede tomar muchas formas: puedes simplemente recomendar a un cliente “comprar barato, vender caro” o dar una presentación oral a tus colegas. Sin embargo, lo más probable es que necesites resumir tus hallazgos en un informe escrito.

Comunicar información técnica es difícil por diversas razones. Primero, en la mayoría de los análisis de datos no hay una “respuesta correcta” que el autor trate de comunicar al lector. Para establecer una “respuesta correcta”, solo es necesario posicionar los pros y los contras de un tema y evaluar sus méritos relativos. En los informes estadísticos, el autor intenta comunicar las características de los datos y su relación con patrones más generales, una tarea mucho más compleja. Segundo, la mayoría de los informes están dirigidos a un cliente o audiencia principal. En contraste, los informes estadísticos suelen ser leídos por muchos lectores diferentes cuyo conocimiento de los conceptos estadísticos varía ampliamente; es importante considerar las características de esta audiencia heterogénea al juzgar el ritmo y orden en que se presenta el material. Esto es particularmente difícil cuando un escritor solo puede suponer quién será la audiencia secundaria. Tercero, los autores de informes estadísticos necesitan tener una base de conocimiento amplia y profunda, incluyendo un buen entendimiento de los temas subyacentes, conocimientos de conceptos estadísticos y habilidades lingüísticas. Combinar estas habilidades puede ser un desafío. Incluso para un escritor generalmente efectivo, cualquier confusión en el análisis inevitablemente se reflejará en el informe.

La comunicación de los resultados del análisis de datos puede ser desde una breve recomendación oral a un cliente hasta una tesis doctoral de 500 páginas. Sin embargo, para la mayoría de los propósitos empresariales, basta con un informe de 10 a 20 páginas que resuma las principales conclusiones y detalle el análisis. Un aspecto clave de dicho informe es proporcionar al lector una comprensión de las características destacadas de los datos. Se deben incluir suficientes detalles del estudio para que el análisis pueda ser replicado de forma independiente con acceso a los datos originales.

20.2 Métodos para Comunicar Datos

Para permitir que los lectores interpreten la información numérica de manera efectiva, los datos deben presentarse utilizando una combinación de palabras, números y gráficos que revelen su complejidad. Por lo tanto, los creadores de presentaciones de datos deben basarse en habilidades provenientes de varias áreas, incluyendo:

un entendimiento del área temática subyacente,
un conocimiento de los conceptos estadísticos relacionados,
una apreciación de los atributos de diseño de las presentaciones de datos y
una comprensión de las características de la audiencia a la que están dirigidos.

Este equilibrio de conocimientos es vital si el propósito de la presentación de datos es informar. Si el propósito es animar los datos (“porque los datos son inherentemente aburridos”) o atraer atención, entonces los atributos de diseño pueden adquirir un papel más destacado. Por el contrario, algunos creadores con fuertes habilidades cuantitativas simplifican las presentaciones de datos en exceso para llegar a una audiencia amplia. Al no utilizar los atributos de diseño adecuados, solo revelan parte de la información numérica y ocultan la verdadera historia de sus datos. Para citar a Albert Einstein, “Deberías hacer tus modelos tan simples como sea posible, pero no más simples”.

Esta sección presenta los elementos básicos y reglas para construir presentaciones de datos exitosas. Con este fin, discutimos tres modos de presentar información numérica: (i) datos dentro del texto, (ii) datos tabulares y (iii) gráficos de datos. Estos tres modos están ordenados aproximadamente por la complejidad de los datos que están diseñados para presentar; desde el modo de datos dentro del texto, que es más útil para representar los tipos más simples de datos, hasta el modo de gráficos de datos, que es capaz de transmitir información numérica de conjuntos de datos extremadamente grandes.

Datos Dentro del Texto

Los datos dentro del texto simplemente se refieren a cantidades numéricas que se citan dentro de la estructura habitual de las oraciones. Por ejemplo:

El precio de la acción de Vigoro hoy es $36.50 por acción, un récord histórico.

Al presentar datos dentro del texto, tendrás que decidir si usar cifras o escribir un número en palabras. Hay varias pautas para elegir entre cifras y palabras, aunque generalmente para la redacción empresarial usarás palabras si esta elección resulta en una declaración concisa. Algunas de las pautas importantes incluyen:

Escribe con palabras los números enteros del uno al noventa y nueve.
Usa cifras para números fraccionarios.
Escribe con palabras los números redondos que son aproximaciones.
Escribe con palabras los números que comienzan una oración.
Usa cifras en oraciones que contienen varios números.

Por ejemplo:

   Hay cuarenta y tres estudiantes en mi clase.

   Con 0.2267 dólares estadounidenses puedo comprar una corona sueca.

   Hay alrededor de cuarenta y tres mil estudiantes en esta universidad.

   Tres mil cuatrocientas cincuenta y seis personas votaron por mí.

   Esos niños tienen 3, 4, 6 y 7 años.

El texto fluye de manera lineal; esto dificulta que el lector haga comparaciones de datos dentro de una oración. Cuando las listas de números se vuelven largas o cuando es importante hacer comparaciones, un dispositivo útil para presentar datos es la tabla dentro del texto, también llamada forma semitabular. Por ejemplo:

Para 2005, las primas netas por las principales líneas de negocio escritas por aseguradoras de bienes y accidentes en miles de millones de dólares estadounidenses fueron:

Auto particular — 159.57
Hogares múltiples riesgos — 53.01
Compensación laboral — 39.73
Otras líneas — 175.09.

(Fuente: The Insurance Information Institute Fact Book 2007.)

Tablas

Cuando la lista de números es más larga, la forma tabular o tabla es la opción preferida para presentar datos. Los elementos básicos de una tabla aparecen en Tabla 20.1.

Tabla 20.1. Estadísticas Resumidas de las Variables de Liquidez de Acciones

\[ \small{ \begin{array}{lrrrrr} \hline & & & \text{Desviación} & & \\ & \text{Media} & \text{Mediana} & \text{Estándar} & \text{Mínimo} & \text{Máximo} \\ \hline \text{VOLUME} & 13.423 & 11.556 & 10.632 & 0.658 & 64.572 \\ \text{AVG}T & 5.441 & 4.284 & 3.853 & 0.590 & 20.772 \\ \text{NTRAN} & 6436 & 5071 & 5310 & 999 & 36420 \\ \text{PRICE} & 38.80 & 34.37 & 21.37 & 9.12 & 122.37 \\ \text{SHARE} & 94.7 & 53.8 & 115.1 & 6.7 & 783.1 \\ \text{VALUE} & 4.116 & 2.065 & 8.157 & 0.115 & 75.437 \\ \text{DEB_EQ} & 2.697 & 1.105 & 6.509 & 0.185 & 53.628 \\\hline \\ \hline \end{array} } \] Fuente: Francis Emory Fitch, Inc., Standard & Poor’s Compustat, y el Centro de Investigación de Precios de Seguridad de la Universidad de Chicago.

Estos son:

Título. Una breve descripción de los datos, ubicada encima o al lado de la tabla. Para documentos más largos, proporcione un número de tabla para facilitar la referencia dentro del cuerpo principal del texto. El título puede ser complementado por observaciones adicionales, formando así una leyenda.
Encabezados de columnas. Indicaciones breves del contenido de las columnas.
Etiqueta. La columna vertical izquierda. A menudo proporciona información identificativa para los elementos individuales de las filas.
Cuerpo. Las demás columnas verticales de la tabla.
Reglas. Líneas que separan la tabla en sus diversos componentes.
Fuente. Proporciona el origen de los datos.

Al igual que con la forma semitabular, las tablas pueden diseñarse para mejorar las comparaciones entre números. A diferencia de la forma semitabular, las tablas están separadas del cuerpo principal del texto. Debido a que están separadas, las tablas deben ser autosuficientes para que el lector pueda obtener información de la tabla con poca referencia al texto. El título debe llamar la atención sobre las características importantes de la tabla. El diseño debe guiar la vista del lector y facilitar las comparaciones. Tabla 20.1 ilustra la aplicación de algunas reglas básicas para construir tablas “amigables para el usuario”. Estas reglas incluyen:

Para títulos y otros encabezados, LAS CADENAS DE MAYÚSCULAS SON DIFÍCILES DE LEER, mantenlas al mínimo.
Reduzca el tamaño físico de una tabla para que la vista no tenga que recorrer tanto como de otro modo; use un espaciado sencillo y reduzca el tamaño de la fuente.
Use columnas para las cifras a comparar en lugar de filas; las columnas son más fáciles de comparar, aunque esto hace que los documentos sean más largos.
Use promedios y totales de filas y columnas para proporcionar enfoque. Esto permite a los lectores hacer comparaciones.
Cuando sea posible, ordene las filas y/o columnas por tamaño para facilitar las comparaciones. En general, ordenar alfabéticamente las categorías hace poco para entender conjuntos de datos complejos.
Use combinaciones de espaciado y reglas horizontales y verticales para facilitar las comparaciones. Las reglas horizontales son útiles para separar categorías principales; las reglas verticales deben usarse con moderación. Los espacios en blanco entre columnas sirven para separar categorías; los pares de columnas estrechamente espaciados fomentan la comparación.
Use sombreado y diferentes tamaños y atributos de fuente para resaltar cifras. El uso de sombreado también es efectivo para romper la apariencia monótona de una tabla grande.
La primera vez que se muestren los datos, proporcione la fuente.

Gráficos

Para representar conjuntos de datos grandes y complejos, o datos donde los valores numéricos reales son menos importantes que las relaciones que se deben establecer, las representaciones gráficas de los datos son útiles. La Figura 20.1 describe algunos de los elementos básicos de un gráfico, también conocido como diagrama, ilustración o figura. Estos incluyen:

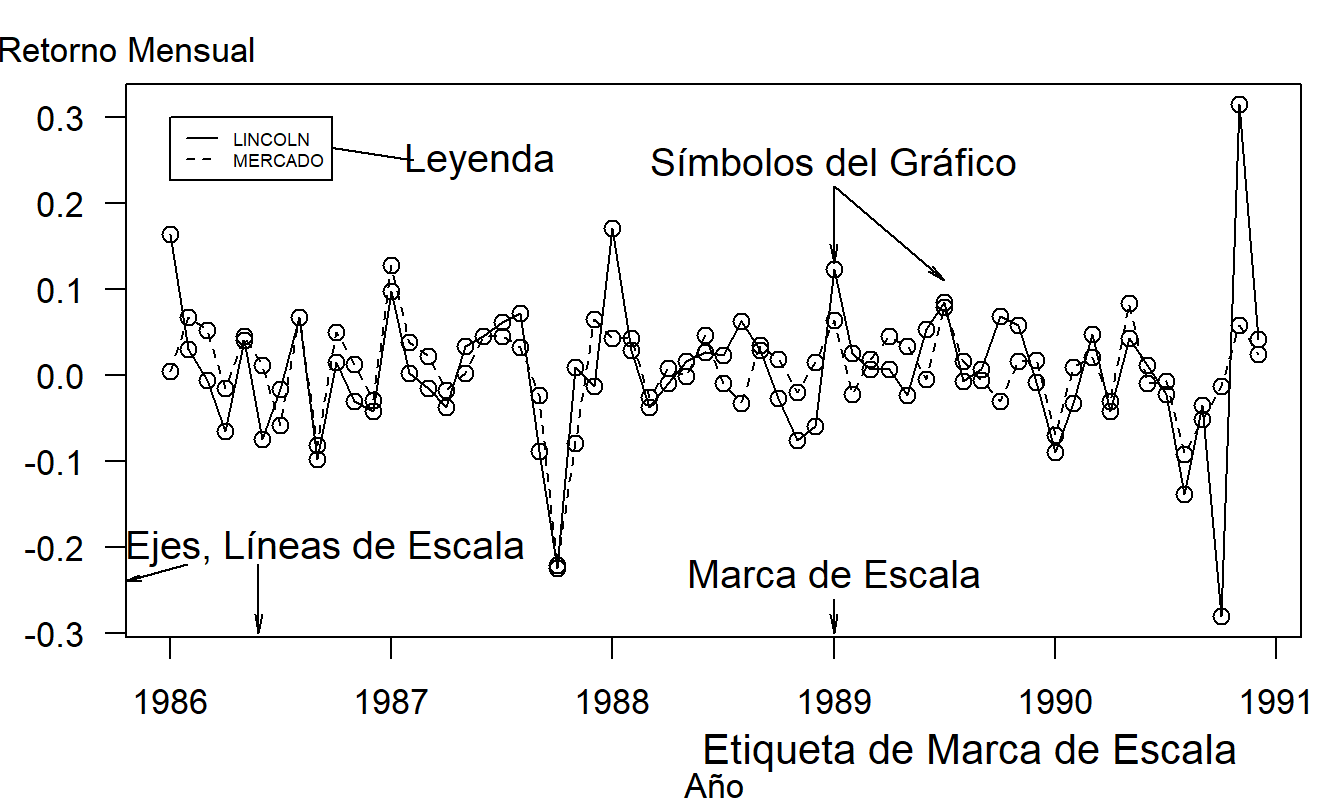
Gráfico de series temporales de los retornos de Lincoln National Corporation y del mercado. Contiene 60 retornos mensuales durante el período de enero de 1986 a diciembre de 1990.

Figura 20.1: Gráfico de series temporales de los retornos de Lincoln National Corporation y del mercado. Contiene 60 retornos mensuales durante el período de enero de 1986 a diciembre de 1990.

Título y Leyenda. Al igual que en una tabla, estos proporcionan breves descripciones de las características principales de la figura. Se pueden utilizar leyendas largas para describir todo lo que se está graficando, llamar la atención sobre las características importantes y describir las conclusiones que se deben extraer de los datos. Incluya la fuente de los datos aquí o en una línea separada inmediatamente debajo del gráfico.
Líneas de escala (Ejes) y Etiquetas de escala. Elija las escalas de manera que los datos llenen la mayor parte posible de la región de datos. No insista en que se incluya el cero; suponga que el espectador observará el rango de las escalas y las comprenderá.
Marcas de escala y Etiquetas de marcas de escala. Elija el rango de las marcas de escala para incluir casi todos los datos. Generalmente, de tres a diez marcas de escala son suficientes. Cuando sea posible, coloque las marcas fuera de la región de datos, para que no interfieran con los datos.
Símbolos de graficado. Use diferentes símbolos de graficado para codificar distintos niveles de una variable. Los símbolos de graficado deben ser fáciles de identificar, por ejemplo, “O” para uno y “T” para dos. Sin embargo, asegúrese de que los símbolos sean fáciles de distinguir; por ejemplo, puede ser difícil diferenciar “F” y “E”.
Leyenda (Claves). Son pequeñas visualizaciones textuales que ayudan a identificar ciertos aspectos de los datos. No permita que estas visualizaciones interfieran con los datos o saturen el gráfico.

Al igual que las tablas, los gráficos están separados del cuerpo principal del texto y, por lo tanto, deben ser autosuficientes. Especialmente en documentos largos, las tablas y gráficos pueden contener una línea narrativa separada, proporcionando una visión del mensaje principal del documento de una manera diferente al cuerpo principal del texto. Cleveland (1994) y Tufte (1990) ofrecen varios consejos para hacer que los gráficos sean más “amigables para el usuario”.

Haga las líneas tan delgadas como sea posible. Las líneas delgadas distraen menos la vista de los datos en comparación con las líneas más gruesas. Sin embargo, haga las líneas lo suficientemente gruesas para que la imagen no se degrade al reproducirla.
Intente usar la menor cantidad de líneas posible. Nuevamente, varias líneas distraen la vista de los datos, que contienen la información. Evite usar líneas de “cuadrícula” si es posible. Si debe usar líneas de cuadrícula, elija una tinta clara, como un gris o medio tono.
Escriba las palabras completas y evite abreviaturas. Raramente vale la pena el espacio ahorrado frente a la confusión potencial que la versión abreviada puede causar al espectador.
Use un tipo de letra que incluya letras mayúsculas y minúsculas.
Coloque los gráficos en la misma página que el texto que discute el gráfico.
Haga que las palabras corran de izquierda a derecha, no en forma vertical.
Use la sustancia de los datos para sugerir la forma y el tamaño del gráfico. Para gráficos de series temporales, haga el gráfico dos veces más ancho que alto. Para diagramas de dispersión, haga el gráfico tan ancho como alto. Si un gráfico muestra un mensaje importante, hágalo grande.

Por supuesto, para la mayoría de los gráficos será imposible seguir simultáneamente todos estos consejos. Para ilustrar, si escribimos la etiqueta de la escala en un eje vertical izquierdo y la hacemos correr de izquierda a derecha, entonces invadimos la escala vertical. Esto nos obliga a reducir el tamaño del gráfico, posiblemente a expensas de reducir el mensaje.

Un gráfico es una herramienta poderosa para resumir y presentar información numérica. Los gráficos pueden romper la monotonía de documentos largos; pueden provocar y mantener el interés del lector. Además, los gráficos pueden revelar aspectos de los datos que otros métodos no pueden.

20.3 Cómo Organizar

Los expertos en redacción coinciden en que los resultados deben presentarse de manera organizada con un flujo lógico, aunque no existe consenso sobre cómo lograr este objetivo. Toda historia tiene un principio y un final, generalmente con un camino interesante que conecta los dos extremos. Hay muchos tipos de caminos, o métodos de desarrollo, que conectan el principio y el final. Para la redacción técnica general, el método de desarrollo puede organizarse cronológicamente, espacialmente, por orden de importancia, de lo general a lo específico o de lo específico a lo general, por causa y efecto o por cualquier otro desarrollo lógico de los temas. Esta sección presenta un método de organización para la redacción de informes estadísticos que ha demostrado ser efectivo en diversas circunstancias, incluido el informe de 10 a 20 páginas descrito anteriormente. Este formato, aunque no es apropiado para todas las situaciones, sirve como una estructura útil sobre la cual basar su primer informe estadístico.

El esquema general del formato recomendado es:

Título y Resumen

Introducción

Características de los Datos

Selección e Interpretación del Modelo

Resumen y Comentarios Finales

Referencias y Apéndice

Las secciones (1) y (2) sirven como material introductorio para orientar al lector. Las secciones (3) y (4) forman el cuerpo principal del informe, mientras que las secciones (5) y (6) constituyen las partes finales.

Título y Resumen

Si su informe se distribuye ampliamente (como espera), aquí hay una noticia desalentadora: la mayoría de su audiencia prevista no pasará del título y el resumen. Incluso para los lectores que lean su informe cuidadosamente, lo que generalmente recordarán serán las impresiones dejadas por el título y el resumen, a menos que sean expertos en el tema (lo que la mayoría de los lectores no serán). Elija cuidadosamente el título de su informe. Debe ser conciso y directo. No incluya expresiones innecesarias (como Un Estudio de, Un Análisis de), pero tampoco sea demasiado breve, por ejemplo, usando títulos de una sola palabra. Además de ser conciso, el título debe ser comprensible, completo y correcto.

El resumen es un breve resumen de uno o dos párrafos sobre su investigación; entre 75 y 200 palabras es una guía razonable. El lenguaje debe ser no técnico, ya que está tratando de llegar a la audiencia más amplia posible. Esta sección debe resumir los principales hallazgos de su informe. Asegúrese de responder preguntas como: ¿Qué problema se estudió? ¿Cómo se estudió? ¿Cuáles fueron los hallazgos? Debido a que está resumiendo no solo sus resultados sino también su informe, generalmente es más eficiente escribir esta sección al final.

Introducción

Al igual que el informe general, la introducción debe dividirse en tres secciones: material de orientación, aspectos clave del informe y un plan del documento.

Para comenzar el material de orientación, reintroduzca el problema al nivel de tecnicidad que desea usar en el informe. Puede ser más o menos técnico que la declaración del problema en el resumen. La introducción establece el ritmo o la velocidad a la que se introducen nuevas ideas en el informe. A lo largo del informe, mantenga un ritmo consistente. Para identificar claramente la naturaleza del problema, en algunos casos, es apropiado incluir una breve revisión de la literatura. La revisión de la literatura cita otros informes que brindan perspectivas sobre aspectos relacionados con el mismo problema. Esto ayuda a cristalizar las características nuevas de su informe.

Como parte de los aspectos clave del informe, identifique la fuente y la naturaleza de los datos utilizados en su estudio. Asegúrese de que sea evidente cómo su conjunto de datos puede abordar el problema planteado. Dé una indicación de la clase de técnicas de modelado que pretende utilizar. ¿Es claro el propósito detrás de esta selección de modelo (por ejemplo, comprensión versus pronóstico)?

En este punto, las cosas pueden volverse un poco complejas para muchos lectores. Es una buena idea proporcionar un esquema del resto del informe al final de la introducción. Esto sirve como un mapa para guiar al lector a través de los argumentos complejos del informe. Además, muchos lectores estarán interesados solo en aspectos específicos del informe y, con el esquema, podrán “avanzar rápidamente” a las secciones que más les interesen.

Características de los Datos

En un proyecto de análisis de datos, el objetivo es resumir los datos y usar esta información resumida para hacer inferencias sobre el estado del mundo. Gran parte de este resumen se realiza a través de estadísticas que se utilizan para estimar parámetros del modelo. Sin embargo, también es útil describir los datos sin hacer referencia a un modelo específico por al menos dos razones. Primero, al usar medidas básicas de resumen de los datos, puede llegar a una audiencia más amplia que si hubiera limitado sus consideraciones a un modelo estadístico específico. De hecho, con un dispositivo gráfico de resumen cuidadosamente construido, debería poder llegar prácticamente a cualquier lector interesado en el material. Por el contrario, la familiaridad con los modelos estadísticos requiere cierta sofisticación matemática, y es posible que desee o no restringir su audiencia en esta etapa del informe. Segundo, construir estadísticas que estén directamente relacionadas con modelos específicos lo expone a críticas si la selección de su modelo es incorrecta. En la mayoría de los informes, la selección de un modelo es un paso inevitable en el proceso de inferencia, pero no es necesario hacerlo en esta etapa relativamente temprana de su informe.

En la sección de características de los datos, identifique la naturaleza de los datos. Por ejemplo, asegúrese de identificar las variables componentes y de indicar si los datos son longitudinales versus transversales, observacionales versus experimentales, etc. Presente cualquier estadística básica de resumen que ayude al lector a desarrollar una comprensión general de los datos. Es una buena idea incluir alrededor de dos gráficos. Use diagramas de dispersión para resaltar relaciones primarias en datos transversales y gráficos de series temporales para indicar las tendencias longitudinales más importantes. Los gráficos y las estadísticas de resumen concomitantes no solo deben destacar las relaciones más importantes, sino que también pueden servir para identificar puntos inusuales que merecen consideración especial. Elija cuidadosamente las estadísticas y resúmenes gráficos que presenta en esta sección. No abrume al lector con una multitud de números. Los detalles presentados en esta sección deben anticipar el desarrollo del modelo en la sección siguiente. Otros aspectos destacados de los datos pueden aparecer en el apéndice.

Selección e Interpretación del Modelo

Esta es la esencia de su informe. Los resultados reportados en esta sección generalmente tomaron más tiempo en lograrse. Sin embargo, la extensión de la sección no necesita ser proporcional al tiempo que le tomó realizar el análisis. Recuerde, está tratando de evitar a los lectores las dificultades que usted atravesó para llegar a sus conclusiones. Sin embargo, al mismo tiempo, desea convencer a los lectores de la solidez de sus recomendaciones. Aquí hay un esquema para la sección de Selección e Interpretación del Modelo que incorpora los elementos clave que deberían aparecer:

Un esquema de la sección

Una declaración del modelo recomendado

Una interpretación del modelo, las estimaciones de los parámetros y cualquier implicación general del modelo

Las justificaciones básicas del modelo

Un esquema del proceso de pensamiento que llevó a este modelo

Una discusión de modelos alternativos

En esta sección, desarrolle sus ideas discutiendo primero los temas generales y los detalles específicos más tarde. Use las subsecciones (1)-(3) para abordar las preocupaciones generales y amplias que un gerente o cliente no técnico podría tener. Los detalles adicionales pueden proporcionarse en las subsecciones (4)-(6) para abordar las inquietudes de los lectores con inclinaciones técnicas. De esta manera, el esquema está diseñado para satisfacer las necesidades de estos dos tipos de lectores. A continuación, se describen con más detalle cada una de las subsecciones.

Usted nuevamente enfrenta los objetivos en conflicto de querer alcanzar a una audiencia lo más amplia posible y, al mismo tiempo, abordar las preocupaciones de los revisores técnicos. Comience esta sección tan importante con un esquema de los temas a tratar. Esto permitirá al lector seleccionar lo que le interese. De hecho, muchos lectores solo querrán examinar su modelo recomendado y las interpretaciones correspondientes, y asumirán que sus justificaciones son confiables. Por lo tanto, después de proporcionar el esquema, brinde inmediatamente una declaración del modelo recomendado sin ambigüedades. Ahora bien, puede no ser claro a partir del conjunto de datos que su modelo recomendado sea superior a otros modelos alternativos y, si ese es el caso, simplemente dígalo. Sin embargo, asegúrese de expresar, sin ambigüedades, lo que consideró mejor. No permita que la confusión que surge de varios modelos en competencia que representan igualmente bien los datos se deslice en su declaración de un modelo.

La declaración de un modelo suele hacerse en terminología estadística, un lenguaje utilizado para expresar ideas del modelo con precisión. Siga inmediatamente la declaración del modelo recomendado con las interpretaciones correspondientes. Las interpretaciones deben realizarse en un lenguaje no técnico. Además de discutir la forma general del modelo, las estimaciones de los parámetros pueden proporcionar una indicación de la fuerza de las relaciones que ha descubierto. A menudo, un modelo se asimila fácilmente por el lector cuando se discute en términos de las implicaciones resultantes, como un intervalo de confianza o de predicción. Aunque es solo un aspecto del modelo, una sola implicación puede ser importante para muchos lectores.

Es una buena idea discutir brevemente algunas de las justificaciones técnicas del modelo en el cuerpo principal del informe. Esto es para convencer al lector de que sabe lo que está haciendo. Por lo tanto, para defender su selección de un modelo, cite algunas de las justificaciones básicas, como estadísticas t, coeficiente de determinación, desviación estándar residual, etc., en el cuerpo principal e incluya argumentos más detallados en el apéndice. Para convencer aún más al lector de que ha reflexionado seriamente sobre el problema, incluya una breve descripción de un proceso de pensamiento que lleve desde los datos hasta su modelo propuesto. No describa al lector todos los problemas que encontró en el camino. Describa, en cambio, un proceso limpio que vincule el modelo con los datos, con la menor complicación posible.

Como se mencionó, en el análisis de datos rara vez hay una “respuesta correcta”. Para convencer al lector de que ha reflexionado profundamente sobre el problema, es una buena idea mencionar modelos alternativos. Esto demostrará que consideró el problema desde más de una perspectiva y que es consciente de que individuos cuidadosos y reflexivos pueden llegar a diferentes conclusiones. Sin embargo, al final, aún necesita dar su modelo recomendado y respaldar su recomendación. Agudizará sus argumentos al discutir un competidor cercano y compararlo con su modelo recomendado.

Resumen y Comentarios Finales

Esta sección debe recapitular los resultados del informe de manera concisa, usando palabras diferentes a las del resumen. El lenguaje puede ser más o menos técnico que el del resumen, dependiendo del tono que estableció en la introducción. Refiérase a las preguntas clave planteadas al inicio del estudio y relacione estas con los resultados. Esta sección puede reflexionar sobre el análisis y servir como punto de partida para preguntas y sugerencias sobre investigaciones futuras. Incluya ideas que tenga sobre futuras investigaciones, teniendo en cuenta los costos y otras consideraciones que puedan estar involucradas en la recopilación de más información.

Referencias y Apéndice

El apéndice puede contener muchas figuras auxiliares y análisis. El lector no le dará al apéndice el mismo nivel de atención que al cuerpo principal del informe. Sin embargo, el apéndice es un lugar útil para incluir muchos detalles cruciales para el lector técnicamente inclinado y características importantes que no son críticas para las principales recomendaciones de su informe. Debido a que el contenido técnico aquí generalmente es más alto que en el cuerpo principal del informe, es importante que cada parte del apéndice esté claramente identificada, especialmente en relación con el cuerpo principal del informe.

20.4 Sugerencias Adicionales para la Redacción de Informes

Sea lo más breve posible, pero incluya todos los detalles importantes. Por un lado, los aspectos clave de varios resultados de regresión a menudo pueden resumirse en una tabla. A menudo, varios gráficos pueden resumirse en una sola oración. Por otro lado, reconozca el valor de un gráfico o tabla bien construidos para transmitir información importante.
Tenga en cuenta a su audiencia al redactar su informe. Explique lo que ahora comprende sobre el problema, con poco énfasis en cómo llegó allí. Brinde interpretaciones prácticas de los resultados, en un lenguaje con el que el cliente se sienta cómodo.
Esquema, esquema. Desarrolle sus ideas de manera lógica, paso a paso. Es vital que haya un flujo lógico en el informe. Comience con un esquema amplio que especifique la estructura básica del informe. Luego haga un esquema más detallado, enumerando cada tema que desea discutir en cada sección. Solo mantendrá la libertad literaria imponiendo estructura a su informe.
Simplicidad, simplicidad, simplicidad. Enfatice sus ideas principales mediante un lenguaje simple. Sustituya palabras complejas por palabras más simples si el significado sigue siendo el mismo. Evite el uso de clichés y lenguaje trillado. Aunque se puede usar lenguaje técnico, evite el uso de jerga técnica o coloquial. La jerga estadística, como “Sea $x_1, x_2, \ldots$ i.i.d. variables aleatorias…”, rara vez es necesaria. Limite el uso de frases en latín (por ejemplo, i.e.) si una frase en inglés o español puede ser suficiente (como “es decir”).
Incluya tablas y gráficos importantes de resumen en el cuerpo del informe. Etiquete todas las figuras y tablas para que sean comprensibles cuando se vean por sí solas.
Use uno o más apéndices para proporcionar detalles de apoyo. Los gráficos de importancia secundaria, como gráficos de residuos, y los resultados del software estadístico, como ajustes de regresión, pueden incluirse en un apéndice. Incluya suficientes detalles para que otro analista, con acceso a los datos, pueda replicar su trabajo. Proporcione un vínculo sólido entre las ideas principales descritas en el cuerpo principal del informe y el material de apoyo en el apéndice.

20.5 Estudio de Caso: Reclamos de Automóviles en Suecia

Determinantes de los Reclamos de Automóviles en Suecia

Resumen

La tarificación de automóviles depende de la capacidad de un actuario para estimar la probabilidad de un reclamo y, en caso de que ocurra, el monto probable. Este estudio examina un conjunto de datos clásico de seguros de automóviles de terceros en Suecia. Se ajustaron modelos de regresión Poisson y gamma para las porciones de frecuencia y severidad, respectivamente. Se demuestra que la distancia recorrida por un vehículo, el área geográfica, la experiencia reciente del conductor en reclamos y el tipo de automóvil son determinantes importantes de la frecuencia de reclamos. Solo el área geográfica y el tipo de automóvil resultan ser determinantes importantes de la severidad de los reclamos. Aunque la experiencia es antigua, las técnicas utilizadas y la importancia de estos determinantes brindan ideas útiles sobre la experiencia actual.

Sección 1. Introducción

Los actuarios buscan establecer primas que sean justas para los consumidores en el sentido de que cada asegurado pague según sus propios reclamos esperados. Estos reclamos esperados se basan en las características del asegurado, que pueden incluir edad, género y experiencia de conducción. La motivación detrás de este principio de tarificación no es completamente altruista; un actuario entiende que una tarificación incorrecta puede llevar a graves consecuencias financieras adversas para la aseguradora. Por ejemplo, si las tarifas son demasiado altas en relación con el mercado, entonces la empresa probablemente no obtendrá una cuota de mercado suficiente. Por el contrario, si las tarifas son demasiado bajas en relación con la experiencia real, las primas recibidas probablemente no cubrirán los reclamos y los gastos relacionados.

Establecer tarifas adecuadas es importante en el seguro de automóviles, que indemniza a los asegurados y a otras partes en caso de un accidente automovilístico. Para una cobertura a corto plazo como el seguro de automóviles, los reclamos resultantes de las pólizas se realizan rápidamente y el actuario puede calibrar la fórmula de tarificación a la experiencia real.

Para muchos analistas, los datos sobre reclamos de seguros pueden ser difíciles de obtener. Las aseguradoras desean proteger la privacidad de sus clientes y, por lo tanto, no quieren compartir datos. Para algunas aseguradoras, los datos no están almacenados en un formato electrónico conveniente para análisis estadísticos; puede ser costoso acceder a los datos incluso si están disponibles para la aseguradora. Quizás lo más importante es que las aseguradoras son reacias a liberar datos al público porque temen divulgar información propietaria que ayude a sus competidores en guerras de precios intensas.

Debido a esta falta de datos actualizados sobre automóviles, este estudio examina un conjunto de datos clásico sueco sobre reclamos de seguros de automóviles de terceros ocurridos en 1977. Los reclamos de terceros implican pagos a alguien que no sea el asegurado y la compañía de seguros, generalmente a alguien lesionado como resultado de un accidente automovilístico. Aunque la experiencia está desactualizada, las técnicas de regresión utilizadas en este informe funcionan igualmente bien con datos actuales. Además, los determinantes de los reclamos investigados, como el uso del vehículo y la experiencia del conductor, probablemente sigan siendo importantes en el mundo de conducción actual.

El esquema del resto de este informe es el siguiente. En la Sección 2, presento las características más importantes de los datos. Para resumir estas características, en la Sección 3 se discute un modelo para representar los datos. En la Sección 4 se encuentran los comentarios finales, y muchos de los detalles del análisis están en el apéndice.

Sección 2. Características de los Datos

Estos datos fueron recopilados por el Comité Sueco para el Análisis de la Prima de Riesgo en el Seguro de Automóviles, resumidos en Hallin e Ingenbleek (1983) y Andrews y Herzberg (1985). Los datos son transversales y describen reclamos de seguros de automóviles de terceros para el año 1977.

Los resultados de interés son el número de reclamos (la frecuencia) y la suma de los pagos (la severidad), en coronas suecas. Los resultados se basan en 5 categorías de distancia recorrida por un vehículo, desglosadas por 7 zonas geográficas, 7 categorías de experiencia reciente del conductor en reclamos (capturada por el “bono”) y 9 tipos de automóviles. Aunque hay 2,205 combinaciones potenciales de distancia, zona, experiencia y tipo ($5 \times 7 \times 7 \times 9 = 2,205$), solo se realizaron $n=2,182$ en el conjunto de datos de 1977. Para cada combinación, además de los resultados de interés, tenemos disponible el número de años de asegurados como medida de exposición. Un “año de asegurado” es la fracción del año en que el asegurado tiene un contrato con la compañía emisora. Explicaciones más detalladas de estas variables están disponibles en el Apéndice A2.

En estos datos, hubo 113,171 reclamos de 2,383,170 años de asegurados, con una tasa de reclamos del 4.75%. De estos reclamos, se pagaron un total de 560,790,681 coronas, con un promedio de 4,955 por reclamo. Como referencia, en junio de 1977, una corona sueca podía intercambiarse por 0.2267 dólares estadounidenses.

Tabla 20.2 proporciona más detalles sobre los resultados de interés. Esta tabla está organizada por las $n=2,182$ combinaciones de distancia, zona, experiencia y tipo. Por ejemplo, la combinación con la mayor exposición (127,687.27 años de asegurados) proviene de aquellos que conducen una cantidad mínima en áreas rurales del sur de Suecia, con al menos seis años sin accidentes y que conducen un automóvil que no es uno de los ocho tipos básicos (Kilómetros=1, Zona=4, Bono=7 y Marca=9, ver Apéndice A2). Esta combinación tuvo 2,894 reclamos con pagos de 15,540,162 coronas. Además, observo que hubo 385 combinaciones que no tuvieron reclamos.

Tabla 20.2. Estadísticas Resumidas de Automóviles en Suecia

\[ \small{ \begin{array}{lrrrrr} \hline & & & \text{Desviación} & & \\ & \text{Media} & \text{Mediana} & \text{Estándar} &\text{ Mínimo} & \text{Máximo} \\ \hline \text{Años de Asegurados } & 1,092.20 & 81.53 & 5,661.16 & 0.01 & 127,687.27 \\ \text{Reclamos} & 51.87 & 5.00 & 201.71 & 0.00 & 3,338.00 \\ \text{Pagos} & 257,008& 27,404 & 1,017,283 & 0 & 18,245,026 \\ \text{Promedio de Reclamos} & 0.069 & 0.051 & 0.086 & 0.000 & 1.667 \\ ~~~ \text{(por Año de Asegurado)} \\ \text{Promedio de Pago} & 5,206.05 & 4,375.00 & 4,524.56 & 72.00 & 31,442.00 \\ ~~~ \text{(por Reclamo)} & \\ \hline \end{array} } \] Nota: Las distribuciones se basan en $n=2,182$ combinaciones de distancia, zona, experiencia y tipo.

Fuente: Hallin e Ingenbleek (1983)

Código R para Generar la Tabla 20.2

	meanSummary	medSummary	sdSummary	minSummary	maxSummary
X1	1092.20	81.53	5661.16	0.01	127687.27
X2	51.87	5.00	201.71	0.00	3338.00
X3	257007.64	27403.50	1017282.59	0.00	18245026.00
X4	0.07	0.05	0.09	0.00	1.67
X5	5206.05	4375.00	4524.56	72.00	31442.00

Tabla 20.2 también muestra la distribución del promedio de reclamos por asegurado. No es sorprendente que el mayor promedio de reclamos ocurriera en una combinación donde solo hubo un reclamo con un pequeño número (0.6) de años de asegurados. Dado que utilizaremos los años de asegurados como un peso en nuestro análisis de la Sección 3, este tipo de comportamiento aberrante se ponderará automáticamente hacia abajo y, por lo tanto, no se requieren técnicas especiales para manejarlo. Para el pago promedio más alto, resulta que hay 27 combinaciones con un solo reclamo de 31,442 (y una combinación con dos reclamos de 31,442). Esto aparentemente representa algún tipo de límite de póliza impuesto del cual no tenemos documentación. Ignoraré esta característica en el análisis.

La Figura 20.2 muestra las relaciones entre los resultados de interés y las bases de exposición. Para el número de reclamos, utilizamos los años de asegurados como la base de exposición. Es claro que el número de reclamos de seguros aumenta con la exposición. Además, los montos de los pagos aumentan con el número de reclamos de manera muy lineal.

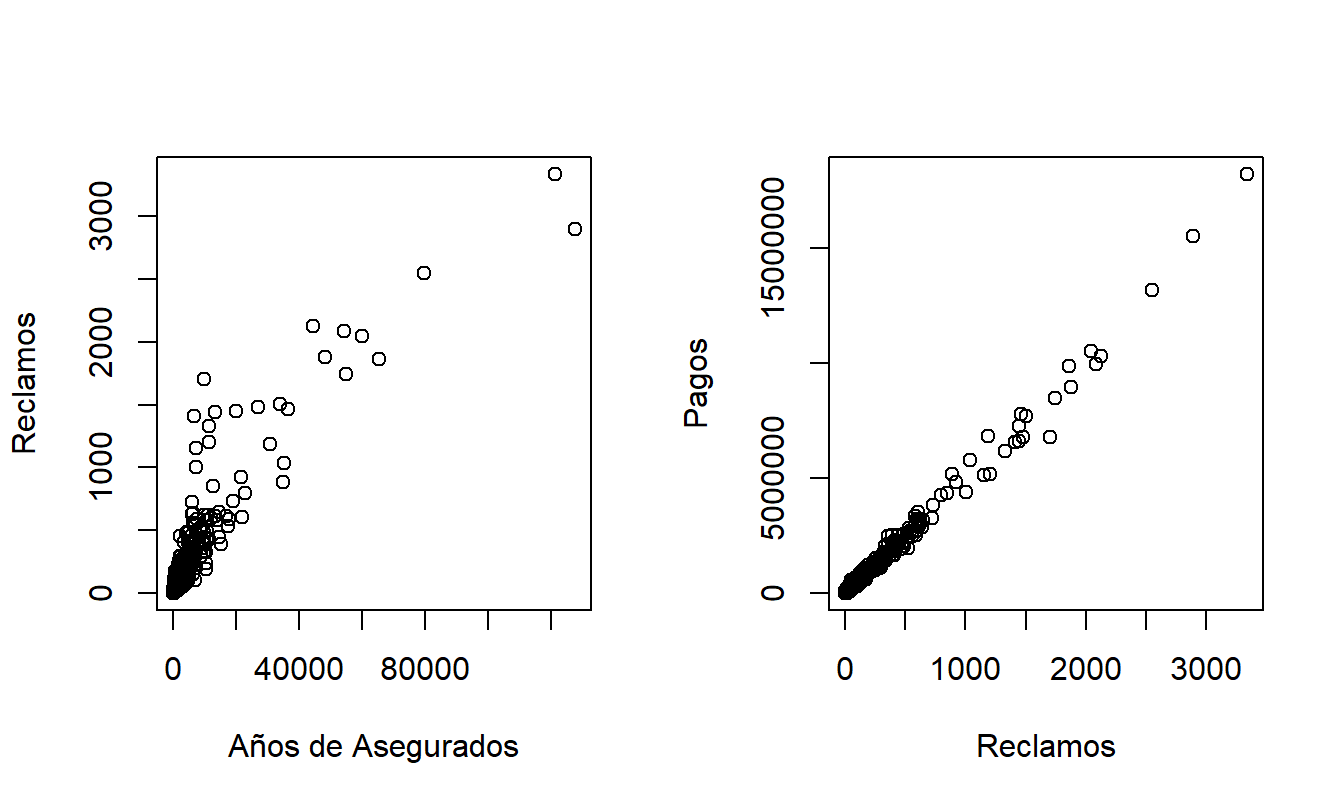
Figura 20.2: Gráficos de Dispersión de Reclamos versus Años de Asegurados y Pagos versus Reclamos.

Código R para Generar la Figura 20.2

Para entender los efectos de las variables explicativas sobre la frecuencia, la Figura 20.3 presenta diagramas de caja del promedio de reclamos por asegurado versus cada variable de clasificación. Para visualizar las relaciones, se han omitido tres combinaciones donde el promedio de reclamos supera 1.0. Esta figura muestra frecuencias más bajas asociadas con distancias de conducción más cortas, ubicaciones no urbanas y un mayor número de años sin accidentes. El tipo de automóvil también parece tener un impacto significativo en la frecuencia de reclamos.

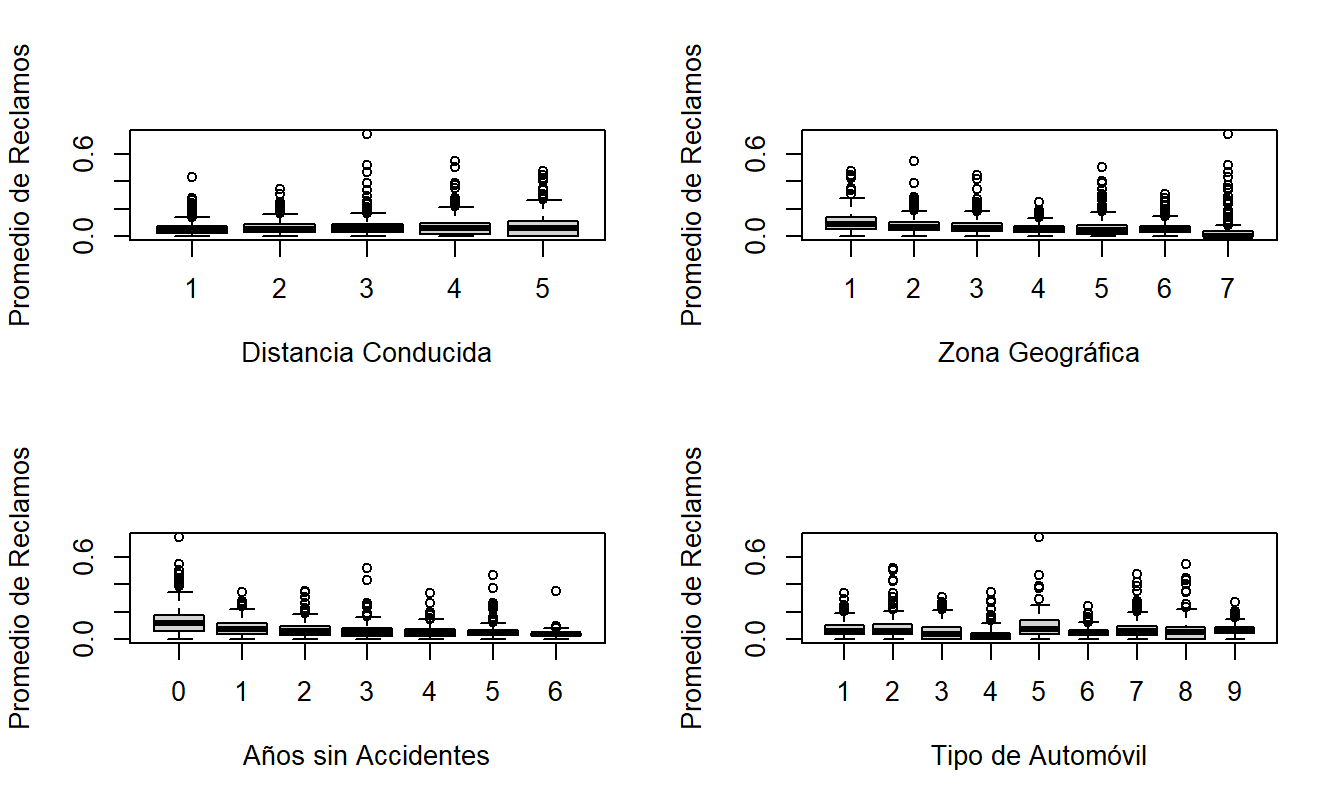
Figura 20.3: Diagramas de Caja de Frecuencia por Distancia Conducida, Zona Geográfica, Años sin Accidentes y Tipo de Automóvil

Código R para Generar la Figura 20.3

Para la severidad, la Figura 20.4 presenta diagramas de caja del pago promedio por reclamo versus cada variable de clasificación. Aquí, los efectos de las variables explicativas no son tan pronunciados como en la frecuencia. El panel superior derecho muestra que la severidad promedio es mucho menor para Zona=7. Esto corresponde a Gotland, un condado y municipio de Suecia que ocupa la isla más grande del Mar Báltico. La Figura 20.4 también sugiere cierta variación según el tipo de automóvil.

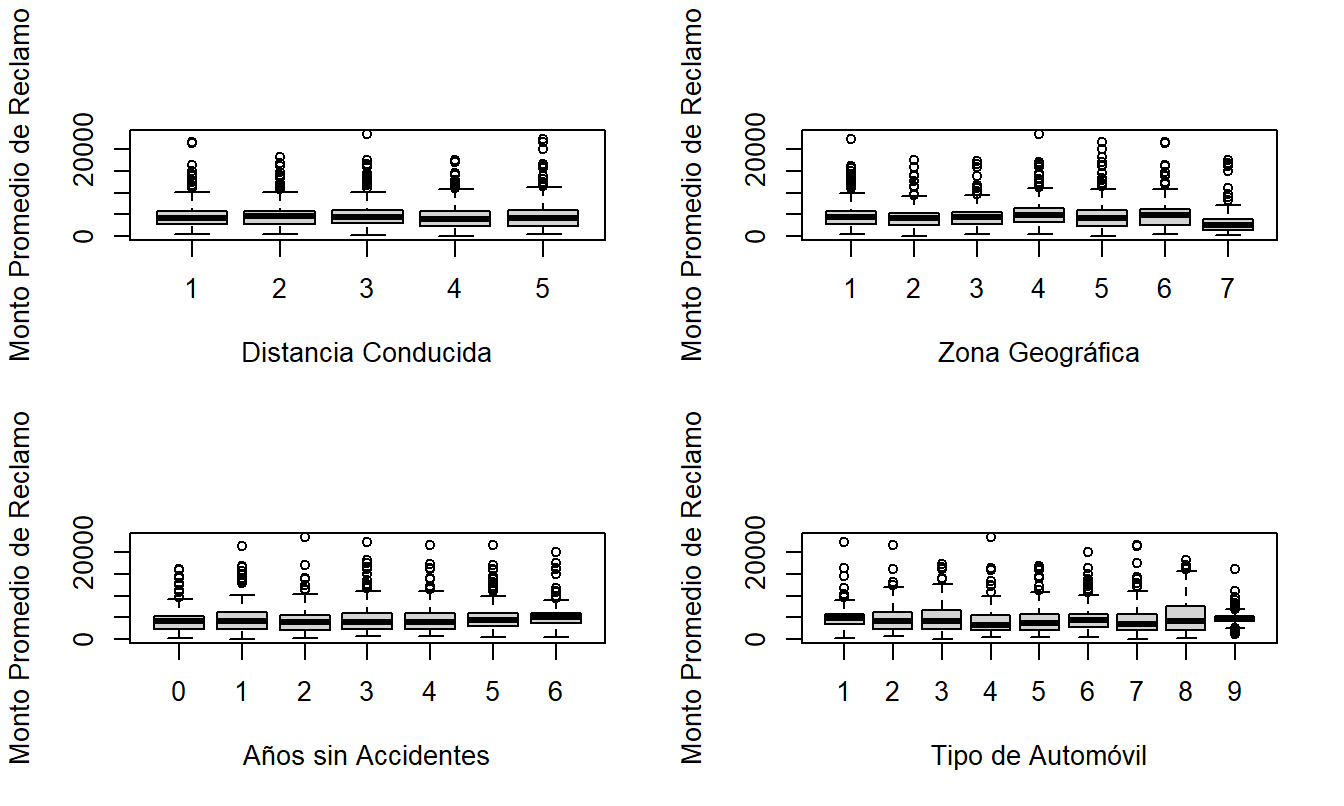
Figura 20.4: Diagramas de Caja de Severidad por Distancia Conducida, Zona Geográfica, Años sin Accidentes y Tipo de Automóvil

Código R para Generar la Figura 20.4

Sección 3. Selección e Interpretación del Modelo

La Sección 2 estableció que existen patrones reales entre la frecuencia y severidad de los reclamos y las variables de clasificación, a pesar de la gran variabilidad en estas variables. Esta sección resume estos patrones utilizando modelos de regresión. Tras la declaración del modelo y su interpretación, esta sección describe características de los datos que motivaron la selección del modelo recomendado.

Como resultado de este estudio, recomiendo un modelo de regresión de Poisson utilizando una función de enlace logarítmica para la parte de frecuencia. El componente sistemático incluye los factores de clasificación distancia, zona, experiencia y tipo como variables categóricas aditivas, así como un término de compensación en el logaritmo del número de asegurados.

Este modelo se ajustó utilizando máxima verosimilitud, con los coeficientes que aparecen en Tabla 20.3; más detalles aparecen en el Apéndice A4. Aquí, las categorías base corresponden al primer nivel de cada factor. Por ejemplo, considere un conductor que vive en Estocolmo (Zona=1), que conduce entre uno y quince mil kilómetros por año (Kilometres=2), ha tenido un accidente en el último año (Bonus=1) y maneja un automóvil del tipo “Make=6”. Entonces, de la Tabla 20.3, el componente sistemático es $-1.813 + 0.213 -0.336 = -1.936.$ Para una póliza típica de esta combinación, estimaríamos un número de reclamos de Poisson con media $\exp(-1.936) = 0.144.$ Por ejemplo, la probabilidad de que no haya reclamos en un año es $\exp(-0.144) = 0.866.$ En 1977, hubo 354.4 años de asegurados en esta combinación, para un número esperado de reclamos de $354.4 \times 0.144 = 51.03.$ Resultó que solo hubo 48 reclamos en esta combinación en 1977.

Table 20.3. Ajuste del Modelo de Regresión de Poisson

\[ \small{ \begin{array}{lrrlrr} \hline \text{Variable} & \text{Coeficiente} & t-\text{ratio} & \text{Variable} & \text{Coeficiente} & t-\text{ratio} \\ \hline \text{Intercepto} & -1.813 & -131.78 & \text{Bonus}=2 & -0.479 & -39.61 \\ \text{Kilometres}=2 & 0.213 & 28.25 & \text{Bonus}=3 & -0.693 & -51.32 \\ \text{Kilometres}=3 & 0.320 & 36.97 & \text{Bonus}=4 & -0.827 & -56.73 \\ \text{Kilometres}=4 & 0.405 & 33.57 & \text{Bonus}=5 & -0.926 & -66.27 \\ \text{Kilometres}=5 & 0.576 & 44.89 & \text{Bonus}=6 & -0.993 & -85.43 \\ \text{Zone}=2 & -0.238 & -25.08 & \text{Bonus}=7 & -1.327 & -152.84 \\ \text{Zone}=3 & -0.386 & -39.96 & \text{Make}=2 & 0.076 & 3.59 \\ \text{Zone}=4 & -0.582 & -67.24 & \text{Make}=3 & -0.247 & -9.86 \\ \text{Zone}=5 & -0.326 & -22.45 & \text{Make}=4 & -0.654 & -27.02 \\ \text{Zone}=6 & -0.526 & -44.31 & \text{Make}=5 & 0.155 & 7.66 \\ \text{Zone}=7 & -0.731 & -17.96 & \text{Make}=6 & -0.336 & -19.31 \\ & & & \text{Make}=7 & -0.056 & -2.40 \\ & & & \text{Make}=8 & -0.044 & -1.39 \\ & & & \text{Make}=9 & -0.068 & -6.84 \\ \hline \end{array} } \]

Código R para Generar la Tabla 20.3

# Tabla 20.3
#Swedish  <- read.csv("CSVData/SwedishMotorInsurance.csv", header=TRUE)
#Swedish  <- read.csv("../../CSVData/SwedishMotorInsurance.csv", header=TRUE)

#Swedish$AveClmNumber <- Swedish$Claims/Swedish$Insured
#Swedish$AveSeverity  <- Swedish$Payment/Swedish$Claims

CountPoisson2 <- glm(Claims ~ factor(Kilometres) + factor(Zone) +
                     factor(Bonus) + factor(Make),
                     offset=log(Insured),poisson(link=log), data = Swedish)
library(modelsummary)
modelsummary(CountPoisson2, output = "html", statistic = "statistic")

	(1)
(Intercept)	−1.813
	(−131.775)
factor(Kilometres)2	0.213
	(28.255)
factor(Kilometres)3	0.320
	(36.974)
factor(Kilometres)4	0.405
	(33.571)
factor(Kilometres)5	0.576
	(44.892)
factor(Zone)2	−0.238
	(−25.082)
factor(Zone)3	−0.386
	(−39.959)
factor(Zone)4	−0.582
	(−67.243)
factor(Zone)5	−0.326
	(−22.446)
factor(Zone)6	−0.526
	(−44.309)
factor(Zone)7	−0.731
	(−17.962)
factor(Bonus)2	−0.479
	(−39.607)
factor(Bonus)3	−0.693
	(−51.316)
factor(Bonus)4	−0.827
	(−56.735)
factor(Bonus)5	−0.926
	(−66.269)
factor(Bonus)6	−0.993
	(−85.429)
factor(Bonus)7	−1.327
	(−152.845)
factor(Make)2	0.076
	(3.590)
factor(Make)3	−0.247
	(−9.859)
factor(Make)4	−0.654
	(−27.022)
factor(Make)5	0.155
	(7.656)
factor(Make)6	−0.336
	(−19.314)
factor(Make)7	−0.056
	(−2.396)
factor(Make)8	−0.044
	(−1.390)
factor(Make)9	−0.068
	(−6.836)
Num.Obs.	2182
AIC	10654.0
BIC	10796.2
Log.Lik.	−5301.998
F	1421.846
RMSE	13.35

Para la parte de severidad, recomiendo un modelo de regresión gamma utilizando una función de enlace logarítmica. El componente sistemático incluye los factores de clasificación zona y tipo como variables categóricas aditivas, así como un término de compensación en el logaritmo del número de reclamos. Además, se utilizó la raíz cuadrada del número de reclamos como variable de ponderación para dar mayor peso a aquellas combinaciones con mayor número de reclamos.

Este modelo se ajustó utilizando máxima verosimilitud, con los coeficientes que aparecen en Tabla 20.4; más detalles aparecen en el Apéndice A6. Considere nuevamente nuestro conductor ilustrativo que vive en Estocolmo (Zone=1), conduce entre uno y quince mil kilómetros por año (=2), ha tenido un accidente en el último año (Bonus=1) y maneja un automóvil del tipo “Make=6”. Para esta persona, el componente sistemático es $8.388 + 0.108 = 8.496.$ Por lo tanto, los reclamos esperados bajo el modelo son $\exp(8.496) = 4,895.$ En comparación, el pago promedio en 1977 fue de 3,467 para esta combinación y 4,955 por reclamo para todas las combinaciones.

Table 20.4. Ajuste del Modelo de Regresión Gamma

\[ \small{ \begin{array}{lrrlrr} \hline \text{Variable} & \text{Coeficiente} & t-\text{ratio} & \text{Variable} & \text{Coeficiente} & t-\text{ratio} \\ \hline Intercepto & 8.388 & 76.72 & \text{Make}=2 & -0.050 & -0.44 \\ \text{Zone}=2 & -0.061 & -0.64 & \text{Make}=3 & 0.253 & 2.22 \\ \text{Zone}=3 & 0.153 & 1.60 & \text{Make}=4 & 0.049 & 0.43 \\ \text{Zone}=4 & 0.092 & 0.94 & \text{Make}=5 & 0.097 & 0.85 \\ \text{Zone}=5 & 0.197 & 2.12 & \text{Make}=6 & 0.108 & 0.92 \\ \text{Zone}=6 & 0.242 & 2.58 & \text{Make}=7 & -0.020 & -0.18 \\ \text{Zone}=7 & 0.106 & 0.98 & \text{Make}=8 & 0.326 & 2.90 \\ & & & \text{Make}=9 & -0.064 & -0.42 \\ Dispersión & 0.483 \\ \hline \end{array} } \]

Código R para Generar la Tabla 20.4

# Tabla 20.4
#Swedish  <- read.csv("CSVData/SwedishMotorInsurance.csv", header=TRUE)
#Swedish  <- read.csv("../../CSVData/SwedishMotorInsurance.csv", header=TRUE)

#Swedish$AveClmNumber <- Swedish$Claims/Swedish$Insured
#Swedish$AveSeverity  <- Swedish$Payment/Swedish$Claims

Swedish3 <- subset(Swedish, Claims>0 )
Swedish3$Weight=1/sqrt(Swedish3$Claims)

Tab204 <- glm(Payment  ~ factor(Zone) + factor(Make), 
              offset=log(Claims), weights=Weight, Gamma(link=log), 
              data = Swedish3)
modelsummary(Tab204, output = "html", statistic = "statistic")

	(1)
(Intercept)	8.388
	(76.722)
factor(Zone)2	−0.061
	(−0.641)
factor(Zone)3	0.153
	(1.597)
factor(Zone)4	0.092
	(0.943)
factor(Zone)5	0.197
	(2.119)
factor(Zone)6	0.242
	(2.581)
factor(Zone)7	0.106
	(0.978)
factor(Make)2	−0.050
	(−0.439)
factor(Make)3	0.253
	(2.219)
factor(Make)4	0.049
	(0.425)
factor(Make)5	0.097
	(0.852)
factor(Make)6	0.108
	(0.925)
factor(Make)7	−0.020
	(−0.180)
factor(Make)8	0.326
	(2.900)
factor(Make)9	−0.064
	(−0.423)
Num.Obs.	1797
AIC	16081.9
BIC	16169.8
Log.Lik.	−8024.959
F	2.879
RMSE	172182.35

Discusión del Modelo de Frecuencia

Ambos modelos proporcionaron un ajuste razonable a los datos disponibles. Para la parte de frecuencia, los $t$-ratios en Tabla 20.3 asociados con cada coeficiente exceden tres en valor absoluto, indicando una fuerte significancia estadística. Además, el Apéndice A5 demuestra que cada factor categórico es estadísticamente significativo.

No se identificaron otros patrones importantes entre los residuales del modelo ajustado final y las variables explicativas. La Figura A1 muestra un histograma de los residuales de desviación, indicando normalidad aproximada, una señal de que los datos son congruentes con los supuestos del modelo.

Se consideraron varios modelos de frecuencia competidores. Tabla 20.5 enumera dos más: un modelo de Poisson sin covariables y un modelo binomial negativo con las mismas covariables que el modelo de Poisson recomendado. Esta tabla muestra que el modelo recomendado es el mejor entre estos tres, basado en el estadístico de bondad de ajuste de Pearson y una versión ponderada por exposición. Recuerde que el estadístico de ajuste de Pearson tiene la forma $\sum (O-E)^2/E$, comparando los valores observados ($O$) con los esperados bajo el modelo ajustado ($E$). La versión ponderada resume $\sum w(O-E)^2/E$, donde nuestras ponderaciones son años de póliza en unidades de 100,000. En cada caso, preferimos modelos con estadísticas más pequeñas. Tabla 20.5 muestra que el modelo recomendado es la elección clara entre los tres competidores.

Table 20.5. Bondad de Ajuste de Pearson para Tres Modelos de Frecuencia

\[ \small{ \begin{array}{lrr} \hline \text{Modelo} & \text{Pearson} & \text{Pearson Ponderado} \\ \hline \text{Poisson sin Covariables} & 44,639 & 653.49 \\ \text{Modelo Final de Poisson} & 3,003 & 6.41 \\ \text{Modelo Binomial Negativo} & 3,077 & 9.03 \\ \hline \end{array} } \]

Código R para Generar la Tabla 20.5

En el desarrollo del modelo final, la primera decisión tomada fue utilizar la distribución de Poisson para los conteos. Esto está en concordancia con la práctica aceptada y debido a que un histograma de los números de reclamos (no mostrado aquí) presentó una distribución sesgada similar a Poisson.

Las covariables mostraron características importantes que podrían afectar la frecuencia, como se muestra en la Sección 2 y el Apéndice A3.

Además de los modelos de Poisson y binomial negativo, también ajusté un modelo cuasi-Poisson con un parámetro adicional para la dispersión. Aunque esto pareció ser útil, finalmente decidí no recomendar esta variación porque el objetivo de tarificación es ajustar valores esperados. Todos los factores de calificación fueron muy estadísticamente significativos con y sin el factor adicional de dispersión, por lo que el parámetro adicional solo agregó complejidad al modelo. Por lo tanto, opté por no incluir este término.

Discusión del Modelo de Severidad

Para el modelo de severidad, los factores categóricos zona y marca son estadísticamente significativos, como se muestra en el Apéndice A7. Aunque no se muestran aquí, los residuos de este modelo fueron adecuados. Los residuos de desviación se distribuyeron aproximadamente de manera normal. Los residuos, al ser reescalados por la raíz cuadrada del número de reclamos, fueron aproximadamente homocedásticos. No se encontraron relaciones evidentes con las variables explicativas.

Este modelo complejo se especificó después de un largo examen de los datos. Basándome en las relaciones evidentes entre los pagos y el número de reclamos en la Figura 20.2, el primer paso fue examinar la distribución de los pagos por reclamo. Esta distribución estaba sesgada, por lo que se intentó ajustar los pagos logarítmicos por reclamo. Después de ajustar las variables explicativas a esta variable dependiente, los residuos del ajuste del modelo fueron heterocedásticos. Estos se ponderaron por la raíz cuadrada del número de reclamos y lograron una homocedasticidad aproximada. Desafortunadamente, como se ve en la Figura A2 del Apéndice, el ajuste sigue siendo deficiente en las colas inferiores de la distribución.

Se siguió un proceso similar utilizando la distribución gamma con una función de enlace logarítmica, con los pagos como la respuesta y el logaritmo del número de reclamos como el término de ajuste. Nuevamente, se estableció la necesidad de la raíz cuadrada del número de reclamos como factor de ponderación. El proceso comenzó con las cuatro variables explicativas, pero se descartaron la distancia y los años sin accidentes debido a su falta de significancia estadística. También creé una variable binaria “Seguro” para indicar que un conductor tenía seis o más años sin accidentes (basándome en mi examen de la Figura 20.4). Sin embargo, esta no resultó ser estadísticamente significativa y no se incluyó en la especificación final del modelo.

Sección 4. Resumen y Conclusiones

Aunque los reclamos de seguros varían significativamente, hemos visto que es posible establecer determinantes importantes del número de reclamos y los pagos. Los modelos de regresión recomendados concluyen que los resultados de los seguros pueden explicarse en términos de la distancia conducida por un vehículo, la zona geográfica, la experiencia reciente del conductor con reclamos y el tipo de automóvil. Se desarrollaron modelos separados para la frecuencia y la severidad de los reclamos. En parte, esto se motivó por la evidencia de que menos variables parecen influir en los montos de los pagos en comparación con el número de reclamos.

Este estudio se basó en 113,171 reclamos de 2,383,170 años de pólizas, por un total de 560,790,681 coronas. Este es un conjunto de datos grande que nos permite desarrollar modelos estadísticos complejos. La forma agrupada de los datos nos permite trabajar con solo $n=2,182$ celdas, relativamente pequeño para los estándares actuales. Los datos no agrupados tendrían la ventaja de permitirnos considerar variables explicativas adicionales. Uno podría conjeturar sobre cualquier número de variables adicionales que podrían incluirse; la edad, el género y el descuento por buen estudiante son algunos buenos candidatos. Cabe señalar que el artículo de Hallin e Ingenbleek (1983) consideró la edad del vehículo: esta variable no se incluyó en mi base de datos porque los analistas responsables de la publicación de los datos consideraron que era un determinante insignificante de los reclamos de seguros.

Además, mi análisis de los datos se basa en la experiencia de 1977 de los conductores suecos. Las lecciones aprendidas de este informe pueden o no transferirse a conductores modernos más cercanos. Sin embargo, las técnicas exploradas en este informe deberían ser inmediatamente aplicables con el conjunto adecuado de datos modernos.

Apéndice

Contenido del Apéndice

Referencias
Definiciones de Variables
Estadísticas Básicas Resumidas para la Frecuencia
Modelo Final Ajustado de Regresión de Frecuencia—Salida de R
Comprobación de la Significancia de los Factores en el Modelo Final Ajustado de Regresión de Frecuencia — Salida de R
Modelo Final Ajustado de Regresión de Severidad—Salida de R
Comprobación de la Significancia de los Factores en el Modelo Final Ajustado de Regresión de Severidad — Salida de R

A1. Referencias

Andrews, D. F. y A. M. Herzberg (1985). Capítulo 68 en: A Collection from Many Fields for the Student and Research Worker, pp. 413-421. Springer, Nueva York.
Hallin, Marc y Jean-Franois Ingenbleek (1983). The Swedish automobile portfolio in 1977: A statistical study. Scandinavian Actuarial Journal 1983: 49-64.

A2. Definiciones de Variables

TABLA A.1. Definiciones de Variables \[ \small{ \begin{array}{ll} \hline \text{Nombre} &\text{Descripción} \\ \hline \text{Kilometres} & \text{Kilómetros recorridos por año} \\ & 1: < 1,000 \\ & 2: 1,000-15,000 \\ & 3: 15,000-20,000 \\ & 4: 20,000-25,000 \\ & 5: > 25,000 \\ \hline \text{Zone} & \text{Zona geográfica} \\ & \text{1: Estocolmo, Gotemburgo, Malmö y alrededores} \\ & \text{2: Otras grandes ciudades y alrededores} \\ & \text{3: Ciudades más pequeñas y alrededores en el sur de Suecia} \\ & \text{4: Áreas rurales en el sur de Suecia} \\ & \text{5: Ciudades más pequeñas y alrededores en el norte de Suecia} \\ & \text{6: Áreas rurales en el norte de Suecia} \\ & \text{7: Gotland} \\ \hline \text{Bonus} & \text{Bono por no reclamos.} \\ & \text{Igual al número de años, más uno, desde el último reclamo.} \\ \text{Make} & \text{1-8 representan ocho modelos de automóviles comunes.} \\ & \text{Todos los demás modelos se combinan en la clase 9.} \\ \text{Exposure} & \text{Cantidad de años de póliza} \\ \text{Claims} & \text{Número de reclamos} \\ \text{Payment} & \text{Valor total de los pagos en coronas suecas} \\ \hline \end{array} } \]

A3. Estadísticas Básicas Resumidas para la Frecuencia

TABLA A.2. Promedios de Reclamos por Asegurado según Factor de Clasificación

Kilometre
     1      2      3      4      5
0.0561 0.0651 0.0718 0.0705 0.0827

Zone
     1      2      3      4      5      6      7
0.1036 0.0795 0.0722 0.0575 0.0626 0.0569 0.0504

Bonus
     1      2      3      4      5      6      7
0.1291 0.0792 0.0676 0.0659 0.0550 0.0524 0.0364

Make
     1      2      3      4      5      6      7      8      9
0.0761 0.0802 0.0576 0.0333 0.0919 0.0543 0.0838 0.0729 0.0712

A4. Modelo Final Ajustado para Frecuencia — Salida de R

Call: glm(formula = Claims ~ factor(Kilometres) + factor(Zone) +
factor(Bonus) +
    factor(Make), family = poisson(link = log), offset = log(Insured))

Deviance Residuals:
   Min      1Q  Median      3Q     Max
-6.985  -0.863  -0.172   0.600   6.401

Coefficients:
                    Estimate Std. Error z value Pr(>|z|)   
(Intercept)         -1.81284    0.01376 -131.78  < 2e-16 ***
factor(Kilometres)2  0.21259    0.00752   28.25  < 2e-16 ***
factor(Kilometres)3  0.32023    0.00866   36.97  < 2e-16 ***
factor(Kilometres)4  0.40466    0.01205   33.57  < 2e-16 ***
factor(Kilometres)5  0.57595    0.01283   44.89  < 2e-16 ***
factor(Zone)2       -0.23817    0.00950  -25.08  < 2e-16 ***
factor(Zone)3       -0.38639    0.00967  -39.96  < 2e-16 ***
factor(Zone)4       -0.58190    0.00865  -67.24  < 2e-16 ***
factor(Zone)5       -0.32613    0.01453  -22.45  < 2e-16 ***
factor(Zone)6       -0.52623    0.01188  -44.31  < 2e-16 ***
factor(Zone)7       -0.73100    0.04070  -17.96  < 2e-16 ***
factor(Bonus)2      -0.47899    0.01209  -39.61  < 2e-16 ***
factor(Bonus)3      -0.69317    0.01351  -51.32  < 2e-16 ***
factor(Bonus)4      -0.82740    0.01458  -56.73  < 2e-16 ***
factor(Bonus)5      -0.92563    0.01397  -66.27  < 2e-16 ***
factor(Bonus)6      -0.99346    0.01163  -85.43  < 2e-16 ***
factor(Bonus)7      -1.32741    0.00868 -152.84  < 2e-16 ***
factor(Make)2        0.07624    0.02124    3.59  0.00033 ***
factor(Make)3       -0.24741    0.02509   -9.86  < 2e-16 ***
factor(Make)4       -0.65352    0.02419  -27.02  < 2e-16 ***
factor(Make)5        0.15492    0.02023    7.66  1.9e-14 ***
factor(Make)6       -0.33558    0.01738  -19.31  < 2e-16 ***
factor(Make)7       -0.05594    0.02334   -2.40  0.01655 *  
factor(Make)8       -0.04393    0.03160   -1.39  0.16449   
factor(Make)9       -0.06805    0.00996   -6.84  8.2e-12 ***
---
Signif. codes:  0  ***  0.001  **  0.01  *  0.05  .  0.1     1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 34070.6  on 2181  degrees of freedom
Residual deviance:  2966.1  on 2157  degrees of freedom AIC: 10654

A5. Verificación de la Significancia de los Factores en el Modelo Final Ajustado para Frecuencia — Salida de R

Analysis of Deviance Table

Terms added sequentially (first to last)
                     Df Deviance Resid. Df Resid. Dev P(>|Chi|)    
NULL                                  2181      34071              
factor(Kilometres)    4     1476      2177      32594  2.0e-318 ***
factor(Zone)          6     6097      2171      26498         0 ***
factor(Bonus)         6    22041      2165       4457         0 ***
factor(Make)          8     1491      2157       2966  1.4e-316 ***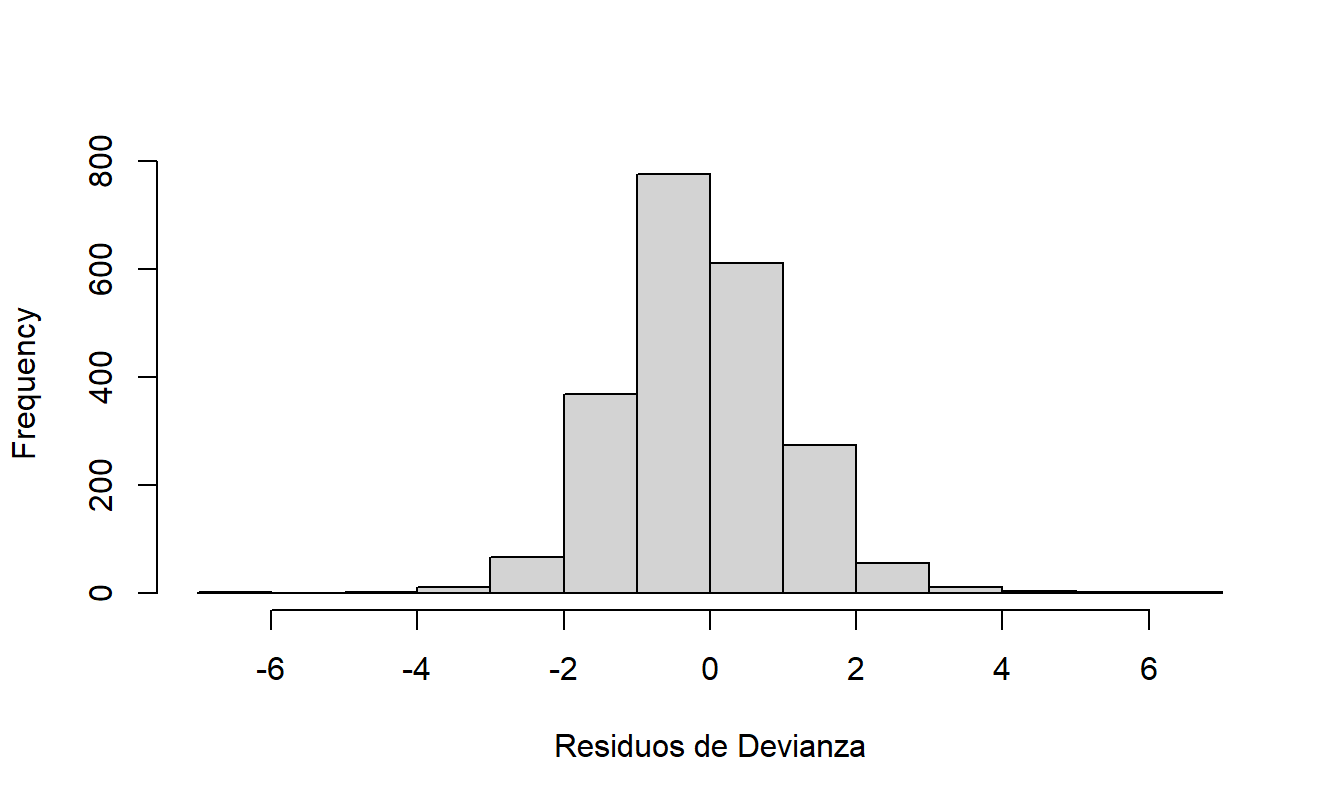

<span style="font-weight: bold;">Figura A1. Histograma de residuos de devianza del modelo final de frecuencia.</span>

Figura 20.5: Figura A1. Histograma de residuos de devianza del modelo final de frecuencia.

A6. Modelo Final Ajustado para Severidad — Salida de R

Call:
glm(formula = Payment ~ factor(Zone) + factor(Make), family = Gamma(link = log),
    weights = Weight, offset = log(Claims))

Deviance Residuals:
     Min        1Q    Median        3Q       Max
-2.56968  -0.39928  -0.06305   0.07179   2.81822

Coefficients:
              Estimate Std. Error t value Pr(>|t|)   
(Intercept)    8.38767    0.10933  76.722  < 2e-16 ***
factor(Zone)2 -0.06099    0.09515  -0.641  0.52156   
factor(Zone)3  0.15290    0.09573   1.597  0.11041   
factor(Zone)4  0.09223    0.09781   0.943  0.34583   
factor(Zone)5  0.19729    0.09313   2.119  0.03427 * 
factor(Zone)6  0.24205    0.09377   2.581  0.00992 **
factor(Zone)7  0.10566    0.10804   0.978  0.32825   
factor(Make)2 -0.04963    0.11306  -0.439  0.66071   
factor(Make)3  0.25309    0.11404   2.219  0.02660 * 
factor(Make)4  0.04948    0.11634   0.425  0.67067   
factor(Make)5  0.09725    0.11419   0.852  0.39454   
factor(Make)6  0.10781    0.11658   0.925  0.35517   
factor(Make)7 -0.02040    0.11313  -0.180  0.85692   
factor(Make)8  0.32623    0.11247   2.900  0.00377 **
factor(Make)9 -0.06377    0.15061  -0.423  0.67205   
---
Signif. codes:  0  ***  0.001  **  0.01  *  0.05  .  0.1     1

(Dispersion parameter for Gamma family taken to be 0.4830309)

    Null deviance: 617.32  on 1796  degrees of freedom
Residual deviance: 596.79  on 1782  degrees of freedom
AIC: 16082

A7. Verificación de la Significancia de los Factores en el Modelo Final Ajustado para Severidad — Salida de R

Analysis of Deviance Table

Terms added sequentially (first to last)

               Df Deviance Resid. Df Resid. Dev P(>|Chi|)    
NULL                            1796     617.32             
factor(Zone)    6     8.06      1790     609.26      0.01 *  
factor(Make)    8    12.47      1782     596.79  0.001130 **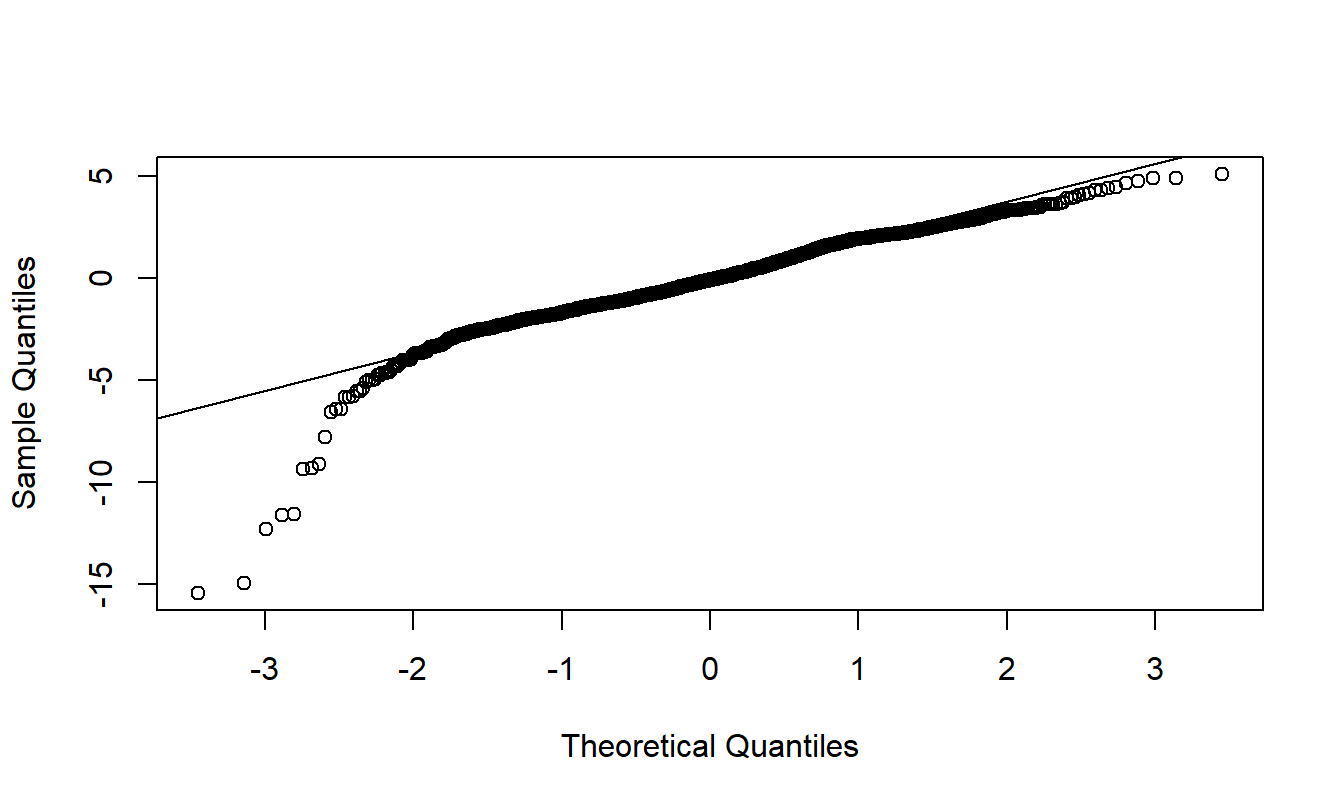

$Figura A2. $qq$ Plot de residuos ponderados de un modelo lognormal. La variable dependiente es la severidad promedio por reclamo. Los pesos son la raíz cuadrada del número de reclamos. El mal ajuste en las colas sugiere usar una alternativa al modelo lognormal.$

Figura 20.6: Figura A2. $qq$ Plot de residuos ponderados de un modelo lognormal. La variable dependiente es la severidad promedio por reclamo. Los pesos son la raíz cuadrada del número de reclamos. El mal ajuste en las colas sugiere usar una alternativa al modelo lognormal.

20.6 Lecturas Adicionales y Referencias

Puede encontrar una discusión adicional sobre las pautas para presentar datos en texto en The Chicago Manual of Style, una referencia conocida para preparar y editar documentos escritos.

Para directrices sobre la presentación de datos en tablas, consulte Ehrenberg (1977) y Tufte (1983).

Miller (2005) es un libro introductorio a la redacción de informes estadísticos con énfasis en métodos de regresión.

Referencias del Capítulo

The Chicago Manual of Style (1993). The University of Chicago Press, 14th ed. Chicago, Ill.
Cleveland, William S. (1994). The Elements of Graphing Data. Monterey, Calif.: Wadsworth.
Ehrenberg, A.S.C. (1977). Rudiments of numeracy. Journal of the Royal Statistical Society A 140:277-97.
Miller, Jane E. (2005). The Chicago Guide to Writing about Multivariate Analysis. The University of Chicago Press, Chicago, Ill.
Tufte, Edward R. (1983). The Visual Display of Quantitative Information. Graphics Press, Cheshire, Connecticut.
Tufte, Edward R. (1990). Envisioning Information. Graphics Press, Cheshire, Connecticut.

20.7 Ejercicio

20.1. Determinantes de la Compensación de CEOs. La compensación de los directores ejecutivos (CEO, por sus siglas en inglés) varía significativamente entre empresas. Para este ejercicio, usted deberá realizar un informe sobre una muestra de empresas tomada de una encuesta de Forbes Magazine para identificar patrones importantes en la compensación de los CEOs.

Específicamente, introduzca un modelo de regresión que explique los salarios de los CEOs en términos de las ventas de la empresa, la experiencia del CEO, su nivel educativo y su participación accionaria en la empresa. Entre otras cosas, este modelo debería mostrar que las empresas más grandes tienden a pagar más a sus CEOs y, algo sorprendente, que los CEOs con un nivel educativo más alto ganan menos que otros CEOs comparables. Además de identificar los factores que influyen en la compensación de los CEOs, este modelo debería usarse para predecir la compensación de los CEOs con fines de negociación salarial.

44638.510	653.495
3002.581	6.413
3077.296	9.031