Capítulo 13 Modelos Lineales Generalizados
Vista Previa del Capítulo. Este capítulo describe un marco unificador para el modelo lineal de la Parte I y los modelos binarios y de conteo en los Capítulos 11 y 12. Los modelos lineales generalizados, conocidos comúnmente por el acrónimo GLM, representan una clase importante de modelos de regresión no lineal que han encontrado un uso extensivo en la práctica actuarial. Este marco unificador no solo abarca muchos de los modelos que hemos visto, sino que también proporciona una plataforma para nuevos modelos, incluyendo las regresiones gamma para datos con colas gruesas y las distribuciones de “Tweedie” para datos de dos partes.
13.1 Introducción
Existen muchas maneras de extender o generalizar el modelo de regresión lineal. Este capítulo introduce una extensión que es tan utilizada que se conoce como el “modelo lineal generalizado”, o por el acrónimo GLM.
Los modelos lineales generalizados incluyen regresiones lineales, logísticas y de Poisson, todas como casos especiales. Una característica común de estos modelos es que en cada caso podemos expresar la media de la respuesta como una función de combinaciones lineales de variables explicativas. En el contexto de los GLM, es habitual usar \(\mu_i = \mathrm{E}~y_i\) para la media de la respuesta y llamar \(\eta_i = \mathbf{x}_i^{\mathbf{\prime}} \boldsymbol \beta\) el componente sistemático del modelo. Hemos visto que podemos expresar el componente sistemático como:
- \(\mathbf{x}_i^{\mathbf{\prime}}\boldsymbol \beta = \mu_i\), para la regresión lineal (normal),
- \(\mathbf{x}_i^{\mathbf{\prime}} \boldsymbol \beta = \exp(\mu_i)/(1+\exp(\mu_i))\), para la regresión logística y
- \(\mathbf{x}_i^{\mathbf{\prime}} \boldsymbol \beta = \ln (\mu_i)\), para la regresión de Poisson.
Para los GLM, el componente sistemático está relacionado con la media a través de la expresión \[\begin{equation} \eta _i = \mathbf{x}_i^{\mathbf{\prime}} \boldsymbol \beta = \mathrm{g}\left( \mu _i\right). \tag{13.1} \end{equation}\] Aquí, g(.) es conocida y se llama función de enlace. La inversa de la función de enlace, \(\mu _i = \mathrm{g}^{-1}( \mathbf{x}_i^{\mathbf{\prime}} \boldsymbol \beta)\), es la función de la media.
La segunda característica común implica la distribución de las variables dependientes. En la Sección 13.2, introduciremos la familia exponencial lineal de distribuciones, una extensión de la distribución exponencial. Esta familia incluye la normal, Bernoulli y Poisson como casos especiales.
La tercera característica común de los modelos GLM es la robustez de la inferencia con respecto a la elección de distribuciones. Aunque la regresión lineal está motivada por la teoría de la distribución normal, hemos visto que las respuestas no necesitan estar distribuidas normalmente para que los procedimientos de inferencia estadística sean efectivos. Las suposiciones de muestreo de la Sección 3.2 se centran en:
- la forma de la función de la media (suposición F1),
- variables explicativas no estocásticas o exógenas (F2),
- varianza constante (F3) y
- independencia entre observaciones (F4).
Los modelos GLM mantienen las suposiciones F2 y F4 y generalizan F1 a través de la función de enlace. La elección de diferentes distribuciones nos permite relajar F3 especificando la varianza como una función de la media, escrita como \(\mathrm{Var~}y_i = \phi v(\mu_i)\). Tabla 13.1 muestra cómo la varianza depende de la media para diferentes distribuciones. Como veremos al considerar la estimación (Sección 13.3), es la elección de la función de varianza la que impulsa las propiedades más importantes de la inferencia, no la elección de la distribución.
Tabla 13.1. Funciones de Varianza para Distribuciones Seleccionadas
\[ \small{ \begin{array}{lc} \hline \text{Distribución} & \text{Función de Varianza }v(\mu) \\ \hline \text{Normal} & 1 \\ \text{Bernoulli} & \mu ( 1- \mu ) \\ \text{Poisson} & \mu \\ \text{Gamma} & \mu ^2 \\ \text{Gaussiana Inversa} & \mu ^3 \\ \hline \end{array} } \]
Al considerar la regresión en el contexto de los GLM, podremos manejar variables dependientes que sean aproximadamente normales, binarias o que representen conteos, todo dentro de un único marco. Esto facilitará nuestra comprensión de la regresión al permitirnos ver el “panorama general” y no preocuparnos tanto por los detalles. Además, la generalidad de los GLM nos permitirá introducir nuevas aplicaciones, como las regresiones gamma, que son útiles para distribuciones con colas gruesas, y las llamadas distribuciones “Tweedie” para datos de dos partes. Los datos de dos partes son un tema que se aborda en el Capítulo 16, donde hay una masa en cero y un componente continuo. En el caso de los datos de reclamaciones de seguros, el cero representa la ausencia de una reclamación y el componente continuo representa el monto de una reclamación.
Este capítulo describe los procedimientos de estimación para calibrar los modelos GLM, pruebas de significancia y estadísticas de bondad de ajuste para documentar la utilidad del modelo, y residuos para evaluar la robustez del ajuste del modelo. Veremos que el trabajo que realizamos anteriormente en modelos de regresión lineal, binaria y de conteo proporciona las bases para las herramientas necesarias para el modelo GLM. De hecho, muchas de estas herramientas y conceptos son ligeras variaciones de lo que ya hemos desarrollado y podremos construir sobre estas bases.
13.2 Modelo GLM
Para especificar un GLM, el analista elige una distribución subyacente de la respuesta, tema de la Sección 13.2.1, y una función que vincula la media de la respuesta con las covariables, tema de la Sección 13.2.2.
13.2.1 Familia Exponencial Lineal de Distribuciones
Definición. La distribución de la familia exponencial lineal es \[\begin{equation} \mathrm{f}(y; \theta, \phi) = \exp \left( \frac{y\theta - b(\theta)}{\phi} + S(y, \phi) \right). \tag{13.2} \end{equation}\] Aquí, \(y\) es una variable dependiente y \(\theta\) es el parámetro de interés. La cantidad \(\phi\) es un parámetro de escala. El término \(b(\theta)\) depende solo del parámetro \(\theta\), no de la variable dependiente. El estadístico \(S(y, \phi)\) es una función de la variable dependiente y el parámetro de escala, pero no del parámetro \(\theta\).
La variable dependiente \(y\) puede ser discreta, continua o una mezcla. Así, \(\mathrm{f}(.)\) puede interpretarse como una función de densidad o de masa, dependiendo de la aplicación. Tabla 13.8 proporciona varios ejemplos, incluyendo las distribuciones normal, binomial y de Poisson. Para ilustrar, consideremos una distribución normal con una función de densidad de probabilidad de la forma: \[\begin{eqnarray*} \mathrm{f}(y; \mu, \sigma^2) &=& \frac{1}{\sigma \sqrt{2\pi}} \exp\left(- \frac{(y-\mu)^2}{2\sigma^2}\right) \\ &=& \exp\left(\frac{(y\mu - \mu^2/2)}{\sigma^2} - \frac{y^2}{2\sigma^2} - \frac{1}{2} \ln(2\pi \sigma^2)\right). \end{eqnarray*}\] Con las elecciones \(\theta = \mu\), \(\phi = \sigma^2\), \(b(\theta) = \theta^2/2\) y \(S(y, \phi) = -y^2/(2\phi) - \ln(2\pi\phi)/2\), vemos que la función de densidad normal puede expresarse como en la ecuación (13.2).
Para la distribución en la ecuación (13.2), algunos cálculos sencillos muestran que:
- \(\mathrm{E~}y = b^{\prime}(\theta)\) y
- \(\mathrm{Var~}y = \phi b^{\prime\prime}(\theta)\).
Para referencia, estos cálculos aparecen en la Sección 13.9.2. Para ilustrar, en el contexto del ejemplo de la distribución normal mencionado arriba, es fácil verificar que \(\mathrm{E~}y = b^{\prime}(\theta) = \theta = \mu\) y \(\mathrm{Var~} y = \sigma^2 b^{\prime\prime}(\theta) = \sigma^2\), como se esperaba.
En situaciones de modelado de regresión, la distribución de \(y_i\) varía por observación a través del subíndice “\(i\)”. Es habitual dejar que la familia de distribuciones permanezca constante, pero permitir que los parámetros varíen por observación utilizando la notación \(\theta_i\) y \(\phi_i\). Para nuestras aplicaciones, la variación del parámetro de escala se debe a factores de peso conocidos. Específicamente, cuando el parámetro de escala varía por observación, se sigue \(\phi_i = \phi / w_i\), es decir, una constante dividida por un peso conocido \(w_i\). Con la relación \(\mathrm{Var~}y_i = \phi_i b^{\prime\prime}(\theta_i) = \phi b^{\prime\prime}(\theta_i) / w_i\), tenemos que un peso mayor implica una varianza menor, todo lo demás constante.
13.2.2 Funciones de Enlace
En situaciones de regresión, deseamos entender el impacto de \(\eta_i = \mathbf{x}_i^{\mathbf{\prime}} \boldsymbol \beta\), el componente sistemático. Como vimos en la subsección anterior, podemos expresar la media de \(y_i\) como \(\mathrm{E~}y_i = \mu_i = b^{\prime}(\theta_i)\). La ecuación (13.1) sirve para “enlazar” el componente sistemático con \(\mu_i\) y, por lo tanto, con el parámetro \(\theta_i\). Es posible usar la función identidad para g(.) de modo que \(\mu_i = b^{\prime}(\theta_i)\). De hecho, este es el caso habitual en la regresión lineal. Sin embargo, las combinaciones lineales de variables explicativas, \(\mathbf{x}_i^{\mathbf{\prime}} \boldsymbol \beta\), pueden variar entre negativo e infinito positivo, mientras que las medias a menudo están restringidas a un rango más pequeño. Por ejemplo, las medias de Poisson varían entre cero e infinito. La función de enlace sirve para mapear el dominio de la función de la media en toda la recta real.
Caso Especial: Enlaces para la distribución Bernoulli. Las medias de Bernoulli son probabilidades y, por lo tanto, varían entre cero y uno. Para este caso, es útil elegir una función de enlace que mapee el intervalo unitario (0,1) en toda la recta real. A continuación se presentan tres ejemplos importantes de funciones de enlace para la distribución Bernoulli:
- Logit: \(g(\mu )=\mathrm{logit}(\mu )=\ln (\mu /(1-\mu ))\) .
- Probit: \(g(\mu )=\Phi ^{-1}(\mu )\), donde \(\Phi ^{-1}\) es la inversa de la función de distribución normal estándar.
- Complementario log-log: \(g(\mu )=\ln \left( -\ln (1-\mu )\right)\).
Esta ilustración demuestra que puede haber varias funciones de enlace que sean adecuadas para una distribución particular. Para ayudar en la selección, un caso intuitivamente atractivo ocurre cuando el componente sistemático es igual al parámetro de interés ($=$). Para ver esto, recordemos primero que \(\eta =g(\mu )\) y \(\mu =b^{\prime }(\theta )\), omitiendo los subíndices “\(i\)” por el momento. Entonces, es fácil ver que si \(g^{-1}=b^{\prime }\), entonces \(\eta =g(b^{\prime }(\theta ))=\theta\). La elección de \(g\) que es la inversa de \(b^{\prime }(\theta )\) se llama el enlace canónico.
Tabla 13.2 muestra la función de la media y el enlace canónico correspondiente para varias distribuciones importantes.
Tabla 13.2. Funciones de Media y Enlaces Canónicos para Distribuciones Seleccionadas
\[ \small{ \begin{array}{lcc} \hline \text{Distribución} & \text{Función de media } b^{\prime }(\theta ) & \text{Enlace canónico }g(\mu ) \\ \hline \text{Normal} & \theta & \mu \\ \text{Bernoulli} & e^{\theta}/(1+e^{\theta} ) & \mathrm{logit}(\mu ) \\ \text{Poisson} & e^{\theta } & \ln \mu \\ \text{Gamma} & -1/\theta & -1/\mu \\ \text{Gaussiana Inversa} & (-2 \theta )^{-1/2} & -1 /(2 \mu^2) \\ \hline \end{array} } \]
Las funciones de enlace relacionan la media con el componente sistemático y con los parámetros de la regresión. Dado que los parámetros de la regresión son desconocidos, es común especificar los enlaces solo hasta la escala. Por ejemplo, es común especificar el enlace canónico para la gaussiana inversa como \(1 /\mu^2\) (en lugar de $-1 /(2 ^2) $). Si es necesario, siempre se puede recuperar la escala al estimar los coeficientes de regresión desconocidos.
Ejemplo: Clasificación para la Fijación de Tarifas. El proceso de agrupar riesgos con características similares se conoce como clasificación de riesgos. La fijación de tarifas es el arte de establecer primas, o tarifas, basadas en la experiencia de pérdidas y las exposiciones de las clases de riesgo. Por ejemplo, Mildenhall (1999) consideró 8,942 pérdidas por colisión de pólizas de seguros de automóviles de uso privado en el Reino Unido (UK). Los datos fueron obtenidos de Nelder y McCullagh (1989, Sección 8.4.1) pero se originaron en Baxter et al. (1980). Un plan de tarifas típico para automóviles personales se basa en las características del conductor y del vehículo. Las características del conductor pueden incluir la edad, género, estado civil, historial (accidentes e infracciones) y descuento por buen estudiante. Las características del vehículo pueden incluir el tipo y año del modelo del vehículo, propósito (negocios/escuela o placer), área de estacionamiento, entre otras. Podemos representar el componente sistemático como:
\[ \eta_{ij} = \beta_0 + \alpha_i + \tau_j, \]
donde \(\alpha_i\) representa el efecto de la \(i\)-ésima categoría de clasificación del conductor y \(\tau_j\) el efecto del \(j\)-ésimo tipo de vehículo. Tabla 13.3 muestra los datos de Mildenhall para ocho tipos de conductores (grupos de edad) y cuatro clases de vehículos (uso del vehículo). La severidad promedio está en libras esterlinas ajustadas por inflación.
En la terminología de GLM, un plan tarifario aditivo se basa en la función de enlace identidad, mientras que un plan multiplicativo se basa en una función de enlace logarítmica. Específicamente, si usamos \(\eta_{ij} = \ln (\mu_{ij})\), entonces podemos escribir la media como:
\[\begin{equation} \mu_{ij} = \exp(\beta_0 + \alpha_i + \tau_j) = B \times A_i \times T_j, \tag{13.3} \end{equation}\]
donde \(B=\exp(\beta_0)\) es una constante de escala, \(A_i=\exp(\alpha_i)\) representa los efectos del conductor y \(T_j=\exp(\tau_j)\) representa los efectos del vehículo.
Tabla 13.3. Datos de Colisiones en Automóviles Privados en el Reino Unido
\[ \scriptsize{ \begin{array}{lcrr|llcrr} \hline \text{Edad} & \text{Uso del} & \text{Severidad} & \text{Número de} &~~~ & \text{Edad} & \text{Uso del} & \text{Severidad} & \text{Número de } \\ & \text{ Vehículo} & \text{Promedio} & \text{Reclamaciones} &~~~ & \text{Edad} & \text{Vehículo} & \text{Promedio} & \text{Reclamaciones} \\ \hline 17-20 & \text{Recreativo} & 250.48 & 21 & & 35-39 & \text{Recreativo} & 153.62 & 151 \\ 17-20 & \text{ConducirCorto} & 274.78 & 40 & & 35-39 & \text{ConducirCorto} & 201.67 & 479 \\ 17-20 & \text{ConducirLargo} & 244.52 & 23 & & 35-39 & \text{ConducirLargo} & 238.21 & 381 \\ 17-20 & \text{Negocios} & 797.80 & 5 & & 35-39 & \text{Negocios} & 256.21 & 166 \\ \hline 21-24 & \text{Recreativo} & 213.71 & 63 & & 40-49 & \text{Recreativo} & 208.59 & 245 \\ 21-24 & \text{ConducirCorto} & 298.60 & 171 & & 40-49 & \text{ConducirCorto} & 202.80 & 970 \\ 21-24 & \text{ConducirLargo} & 298.13 & 92 & & 40-49 & \text{ConducirLargo} & 236.06 & 719 \\ 21-24 & \text{Negocios} & 362.23 & 44 & & 40-49 & \text{Negocios} & 352.49 & 304 \\ \hline 25-29 & \text{Recreativo} & 250.57 & 140 & & 50-59 & \text{Recreativo} & 207.57 & 266 \\ 25-29 & \text{ConducirCorto} & 248.56 & 343 & & 50-59 & \text{ConducirCorto} & 202.67 & 859 \\ 25-29 & \text{ConducirLargo} & 297.90 & 318 & & 50-59 & \text{ConducirLargo} & 253.63 & 504 \\ 25-29 & \text{Negocios} & 342.31 & 129 & & 50-59 & \text{Negocios} & 340.56 & 162 \\ \hline 30-34 & \text{Recreativo} & 229.09 & 123 & & 60+ & \text{Recreativo} & 192.00 & 260 \\ 30-34 & \text{ConducirCorto} & 228.48 & 448 & & 60+ & \text{ConducirCorto} & 196.33 & 578 \\ 30-34 & \text{ConducirLargo} & 293.87 & 361 & & 60+ & \text{ConducirLargo} & 259.79 & 312 \\ 30-34 & \text{Negocios} & 367.46 & 169 & & 60+ & \text{Negocios} & 342.58 & 96 \\ \hline \end{array} } \]
Fuente: Mildenhall (1999). “ConducirCorto” significa conducir al trabajo menos de 10 millas. “ConducirLargo” significa conducir al trabajo más de 10 millas.
Código en R para Generar la Tabla 13.3
13.3 Estimación
Esta sección presenta la estimación por máxima verosimilitud, la forma habitual de estimación. Para proporcionar una intuición, nos enfocamos en el caso más simple de enlaces canónicos. Los resultados para enlaces más generales aparecen en la Sección 13.9.3.
13.3.1 Estimación de Máxima Verosimilitud para Enlaces Canónicos
A partir de la ecuación (13.2) y la independencia entre las observaciones, la función de log-verosimilitud es:
\[\begin{equation} \ln \mathrm{f}( \mathbf{y}) =\sum_{i=1}^n \left\{ \frac{y_i\theta_i-b(\theta_i)}{\phi _i}+S( y_i,\phi _i ) \right\} . \tag{13.4} \end{equation}\]
Recuerda que para enlaces canónicos, tenemos la igualdad entre el parámetro de la distribución y el componente sistemático, de modo que \(\theta_i=\eta _i=\mathbf{x}_i^{\mathbf{\prime }}\boldsymbol \beta\). Así, con \(\phi _i=\phi /w_i\), la función de log-verosimilitud es:
\[\begin{equation} L (\boldsymbol \beta, \phi ) = \ln \mathrm{f}( \mathbf{y}) =\sum_{i=1}^n \left\{ \frac{y_i\mathbf{x}_i^{\mathbf{\prime }}\boldsymbol \beta-b(\mathbf{x}_i^{\mathbf{\prime }} \boldsymbol \beta)}{\phi / w_i}+S( y_i,\phi / w_i) \right\} . \tag{13.5} \end{equation}\]
Al tomar la derivada parcial con respecto a \(\boldsymbol \beta\), obtenemos la función de puntuación:
\[\begin{equation} \frac{\partial }{\partial \boldsymbol \beta} L( \boldsymbol \beta, \phi ) = \frac{1}{\phi} \sum_{i=1}^n \left( y_i-b^{\prime }(\mathbf{x}_i^{\mathbf{\prime }}\boldsymbol \beta) \right) w_i \mathbf{x}_i . \tag{13.6} \end{equation}\]
Dado que \(\mu _i=b^{\prime }(\theta_i)=b^{\prime }(\mathbf{x}_i^{\mathbf{\prime }}\boldsymbol \beta)\), podemos resolver para los estimadores de máxima verosimilitud de \(\boldsymbol \beta\), \(\mathbf{b}_{MLE}\), a través de las “ecuaciones normales”:
\[\begin{equation} \mathbf{0}=\sum_{i=1}^n w_i \left( y_i-\mu _i\right) \mathbf{x}_i. \tag{13.7} \end{equation}\]
Estas ecuaciones representan un sistema con \(k+1\) ecuaciones y \(k+1\) incógnitas. Normalmente, la solución es única y usamos la notación \(\mathbf{b}_{MLE}\) para denotar la solución. Una de las razones del uso generalizado de los métodos GLM es que los estimadores de máxima verosimilitud pueden calcularse rápidamente mediante una técnica conocida como mínimos cuadrados iterados ponderados, descrita en la Sección 13.9.4.
Ten en cuenta que, al igual que en las ecuaciones normales de la regresión lineal ordinaria, no necesitamos considerar la estimación del parámetro de escala de la varianza \(\phi\) en esta etapa. Es decir, primero podemos calcular \(\mathbf{b}_{MLE}\) y, cuando sea necesario, estimar \(\phi\). (Para ciertas distribuciones como la binomial y la de Poisson, \(\phi\) es conocido y no requiere estimación).
Como se describe en la Sección 11.9, los estimadores de máxima verosimilitud son consistentes y tienen distribuciones normales para muestras grandes bajo condiciones generales. La inferencia de máxima verosimilitud proporciona un mecanismo para calcular esta distribución. A partir de las ecuaciones (13.6) y del suplemento técnico sobre la verosimilitud (Sección 11.9, ecuación 11.14), la matriz de información correspondiente es:
\[\begin{equation} \mathbf{I} \left( \mathbf{b}_{MLE} \right) = \frac{1}{\phi}\sum_{i=1}^n w_i ~b^{\prime \prime }(\mathbf{x}_i^{\mathbf{\prime }} \mathbf{b}_{MLE} ) ~ \mathbf{x}_i \mathbf{x}_i^{\mathbf{\prime }} . \tag{13.8} \end{equation}\]
La inversa de la matriz de información es la matriz de varianza-covarianza para muestras grandes de \(\mathbf{b}_{MLE}\). Específicamente, la raíz cuadrada del \((j+1)\)-ésimo elemento diagonal de la inversa de esta matriz proporciona el error estándar para \(b_{j,MLE}\), el cual denotamos como \(se(b_{j,MLE})\). Las extensiones a enlaces generales son similares.
La inferencia para \(\mathbf{b}_{MLE}\) es robusta en cuanto a la elección de distribuciones en el siguiente sentido: la solución de los estimadores de máxima verosimilitud en la ecuación (13.7) depende solo de la función de media; se puede demostrar que la consistencia de los estimadores depende únicamente de la correcta elección de esta función. Además, el comportamiento de muestra grande de \(\mathbf{b}_{MLE}\) esencialmente solo requiere que la media y la varianza sean especificadas correctamente, no la elección de la distribución. (Se requieren algunas condiciones adicionales de regularidad, pero estas son requisitos técnicos leves). Por ejemplo, supongamos que un analista elige una distribución de Poisson con un enlace logarítmico. Si el enlace logarítmico es apropiado, solo se necesita la igualdad entre la media y la varianza, ver Tabla 13.1. A diferencia del dominio usual de la distribución de Poisson, las variables dependientes podrían ser no enteras o incluso negativas. La inferencia para \(\mathbf{b}_{MLE}\) en muestras grandes solo requiere que se elijan correctamente las funciones de media y varianza.
Ejemplo: Clasificación de Tarifas - Continuación. Utilizando los datos en la Tabla 13.3, se ajustó una función de enlace logarítmico con una distribución gamma utilizando el número de reclamaciones como pesos (\(w_i\)). La Tabla 13.4 muestra las estimaciones de la severidad esperada utilizando la ecuación (13.3). Los promedios sugieren que los conductores jóvenes (edades 17-20 y 21-24) tienen las reclamaciones más altas. En cuanto al uso del vehículo, aquellos que conducen por placer tuvieron las reclamaciones más bajas, mientras que aquellos que conducen por negocios tuvieron las reclamaciones más altas.
Tabla 13.4. Estimación de la Severidad Esperada para un Plan Tarifario Multiplicativo
\[ \small{ \begin{array}{l|rrrr|r} \hline \text{Grupo de Edad } & \text{ConducirCorto }& \text{ConducirLargo} & \text{Placer} & \text{Negocios} & \text{Promedio} \\ \hline 17-20 & 322.17 & 265.56 & 254.90 & 419.07 & 315.42 \\ 21-24 & 320.66 & 264.31 & 253.70 & 417.10 & 313.94 \\ 25-29 & 297.26 & 245.02 & 235.19 & 386.66 & 291.03 \\ 30-34 & 284.85 & 234.80 & 225.37 & 370.53 & 278.89 \\ 35-39 & 229.37 & 189.06 & 181.47 & 298.35 & 224.56 \\ 40-49 & 248.15 & 204.54 & 196.33 & 322.78 & 242.95 \\ 50-59 & 251.95 & 207.67 & 199.34 & 327.72 & 246.67 \\ 60+ & 246.47 & 203.16 & 195.00 & 320.60 & 241.31 \\ \hline Promedio & 275.11 & 226.77 & 217.66 & 357.85 & 269.35 \\ \hline \end{array} } \]
Código en R para Generar la Tabla 13.4
13.3.2 Sobredispersión
Para algunos miembros de la familia exponencial lineal, como las distribuciones Bernoulli y Poisson, la varianza está determinada por la media. En contraste, la distribución normal tiene un parámetro de escala separado. Al ajustar modelos a datos con variables dependientes binarias o de conteo, es común observar que la varianza excede la anticipada por el ajuste de los parámetros de la media. Este fenómeno se conoce como sobredispersión. Existen varios modelos probabilísticos alternativos disponibles para explicar este fenómeno, dependiendo de la aplicación en cuestión. Ver la Sección 12.3 para un ejemplo y McCullagh y Nelder (1989) para un inventario más detallado.
Aunque llegar a un modelo probabilístico satisfactorio es el camino más deseable, en muchas situaciones los analistas se conforman con postular un modelo aproximado mediante la relación: \[ \mathrm{Var~}y_i=\sigma ^{2}\phi ~b^{\prime \prime }(\theta_i)/w_i. \] El parámetro \(\phi\) se especifica a través de la elección de la distribución, mientras que el parámetro de escala \(\sigma ^{2}\) permite una variabilidad extra. Por ejemplo, la Tabla 13.8 muestra que al especificar ya sea la distribución Bernoulli o Poisson, tenemos \(\phi =1\). Aunque el parámetro de escala \(\sigma ^{2}\) permite una variabilidad adicional, también puede acomodar situaciones en las que la variabilidad es menor de la especificada por la forma de la distribución (aunque esta situación es menos común). Finalmente, cabe destacar que para algunas distribuciones, como la normal, el término adicional ya está incorporado en el parámetro \(\phi\), por lo que no tiene un propósito útil.
Cuando se incluye el parámetro de escala adicional \(\sigma ^{2}\), es común estimarlo mediante el estadístico chi-cuadrado de Pearson dividido por los grados de libertad del error. Es decir, \[ \widehat{\sigma }^{2}=\frac{1}{N-k} \sum_{i=1}^n w_i\frac{\left( y_i-b^{\prime }(\mathbf{x}_i^{\mathbf{\prime }}\mathbf{b}_{MLE})\right) ^{2}}{\phi b^{\prime \prime }(\mathbf{x}_i^{\mathbf{\prime }}\mathbf{b}_{MLE})}. \] Al igual que con la distribución Poisson en la Sección 12.3, otra forma de manejar patrones inusuales de varianza es a través de errores estándar robustos o empíricos. La Sección 13.9.3 proporciona más detalles.
13.3.3 Estadísticas de Bondad de Ajuste
En los modelos de regresión lineal, la estadística de bondad de ajuste más ampliamente citada es la medida \(R^2\), que se basa en la descomposición \[ \sum_i \left(y_i - \overline{y} \right)^2 = \sum_i \left(y_i - \widehat{y}_i \right)^2 + \sum_i \left(\widehat{y}_i - \overline{y}\right)^2 + 2 \times \sum_i \left(y_i - \widehat{y}_i \right)\left(\widehat{y}_i - \overline{y}\right). \] En el lenguaje de la Sección 2.3, esta descomposición es:
\[ \textit{Total SS = Error SS + Regresión SS + 2} \times \textit{Suma de Productos Cruzados}. \]
La dificultad con los modelos no lineales es que el término de Suma de Productos Cruzados rara vez es igual a cero. Por lo tanto, se obtienen estadísticas diferentes al definir \(R^2\) como (Regresión SS/Total SS) en comparación con (1-Error SS/Total SS). La Sección 11.3.2 describió algunas medidas alternativas de \(R^2\) que a veces se citan en configuraciones GLM.
Una medida de bondad de ajuste ampliamente citada es el estadístico chi-cuadrado de Pearson, que fue introducido en la Sección 12.1.4. En el contexto GLM, suponemos que \(\mathrm{E~}y_i = \mu_i\), \(\mathrm{Var~}y_i = \phi v(\mu_i)\) es la función de varianza (como en los ejemplos de la Tabla 13.1) y que \(\widehat{\mu}_i\) es un estimador de \(\mu_i\). Luego, el estadístico chi-cuadrado de Pearson se define como \(\sum_i \left( y_i - \widehat{\mu}_i \right)^2/\ ( \phi v(\widehat{\mu}_i))\). Como hemos visto en los modelos de Poisson para datos de conteo, esta formulación se reduce a la forma \(\sum_i \left( y_i - \widehat{\mu}_i \right)^2/\widehat{\mu}_i\).
Los criterios de información generales, incluyendo \(AIC\) y \(BIC\), que fueron definidos en la Sección 11.9 también se citan regularmente en estudios de GLM.
Una medida de bondad de ajuste específica para los modelos GLM es la estadística de devianza. Para definir esta estadística, trabajamos con la noción de un modelo saturado donde hay tantos parámetros como observaciones, \(\theta_i, i=1, \ldots, n\). Un modelo saturado proporciona el mejor ajuste posible. Con un parámetro para cada observación, maximizamos la verosimilitud en una base de observación por observación. Por lo tanto, al derivar la verosimilitud logarítmica de la ecuación (13.2) se obtiene \[ \frac{\partial}{\partial \theta_i} \ln \mathrm{f}( y_i; \theta_i ,\phi ) = \frac{y_i-b^{\prime}(\theta_i)}{\phi}. \] Al igualar esto a cero, se obtiene la estimación del parámetro, digamos \(\theta_{i,SAT}\), como la solución de \(y_i=b^{\prime}(\theta_{i,Sat})\). Denotando \(\boldsymbol \theta _{SAT}\) como el vector de parámetros, la verosimilitud \(L(\boldsymbol \theta _{SAT})\) es el valor máximo posible de la verosimilitud logarítmica. Luego, para un estimador genérico \(\widehat{\boldsymbol \theta}\), la estadística de devianza escalada se define como \[ \mathbf{\mathrm{D}}^{\ast}(\widehat{\boldsymbol \theta}) = 2 \times \left( L(\boldsymbol \theta _{SAT}) - L(\widehat{\boldsymbol \theta}) \right). \] En las familias exponenciales lineales, se multiplica por el factor de escala \(\phi\) para definir la estadística de devianza, \(\mathbf{\mathrm{D}}(\widehat{\boldsymbol \theta}) = \phi \mathbf{\mathrm{D}}^{\ast}(\widehat{\boldsymbol \theta})\). Esta multiplicación realmente elimina el factor de escala de la varianza de la definición de la estadística.
Es fácil verificar que la estadística de devianza se reduce a las siguientes formas para tres casos especiales:
- Normal: \(\mathbf{\mathrm{D}}(\widehat{\boldsymbol \mu})= \sum_i \left( y_i - \widehat \mu _i \right) ^2\),
- Bernoulli: \(\mathbf{\mathrm{D}}(\widehat{\boldsymbol \pi})= \sum_i \left\{ y_i \ln \frac {y_i}{\widehat \pi_i} + (1-y_i) \ln \frac {1-y_i}{1-\widehat \pi_i} \right\}\), y
- Poisson: \(\mathbf{\mathrm{D}}(\widehat{\boldsymbol \mu})= \sum_i \left\{ y_i \ln \frac {y_i}{\widehat \mu_i} + (y_i - \widehat \mu _i) \right\}\).
Aquí usamos la convención de que \(y \ln y = 0\) cuando \(y = 0\).
13.4 Aplicación: Gastos Médicos
Ahora volvemos a los datos de la Encuesta del Panel de Gastos Médicos (MEPS) introducidos en la Sección 11.4. En esa sección, buscamos desarrollar un modelo para entender el evento de una admisión hospitalaria como paciente interno. En esta sección, ahora deseamos modelar la cantidad del gasto. En terminología actuarial, la Sección 11.4 consideraba la “frecuencia”, mientras que esta sección involucra la “severidad”.
De las 2,000 observaciones seleccionadas aleatoriamente del año 2003 consideradas en la Sección 11.4, solo \(n=157\) fueron admitidos al hospital durante el año. La Tabla 13.5 resume los datos utilizando las mismas variables explicativas que en la Tabla 11.4. Por ejemplo, la Tabla 13.5 muestra que la muestra es 72% femenina, casi 76% blanca y más del 91% tiene seguro. La tabla también muestra relativamente pocos gastos por parte de asiáticos, nativos americanos y personas sin seguro en nuestra muestra.
La Tabla 13.5 también proporciona los gastos medianos por variable categórica. Esta tabla sugiere que el género, una mala autoevaluación de la salud física y los ingresos bajos o negativos pueden ser determinantes importantes de la cantidad de los gastos médicos.
Tabla 13.5. Gastos Medianos por Variable Explicativa Basado en una Muestra de \(n=157\) con Gastos Positivos
\[ \scriptsize{ \begin{array}{lllrr} \hline \text{Categoría} & \text{Variable} & \text{Descripción} & \text{Porcentaje} & \text{Mediana} \\ & & & \text{de datos} & \text{Gasto} \\ \hline & COUNTIP & \text{Número de gastos (mediana: 1.0)} \\ \text{Demografía} & AGE & \text{Edad en años entre } \\ & & \ \ \ \text{ 18 a 65 (mediana: 41.0)} \\ & GENDER & \text{1 si es mujer} & 72.0 & 5,546 \\ & & \text{0 si es hombre} & 28.0 & 7,313 \\ \text{Etnicidad} & ASIAN & \text{1 si es asiático} & 2.6 & 4,003 \\ & BLACK & \text{1 si es afroamericano} & 19.8 & 6,100 \\ & NATIVE & \text{1 si es nativo} & 1.9 & 2,310 \\ & WHITE & \textit{Nivel de referencia} & 75.6 & 5,695 \\ \text{Región} & NORTHEAST & \text{1 si es del noreste} & 18.5 & 5,833 \\ & MIDWEST & \text{1 si es del medio oeste} & 21.7 & 7,999 \\ & SOUTH & \text{1 si es del sur} & 40.8 & 5,595 \\ & WEST & \textit{Nivel de referencia} & 19.1 & 4,297 \\ \hline \text{Educación} & COLLEGE & \text{1 si tiene título universitario o superior} & 23.6 & 5,611 \\ & \text{HIGHSCHOOL} & \text{1 si tiene título de secundaria} & 43.3 & 5,907 \\ && \text{Nivel de referencia es menor} & 33.1 & 5,338 \\ && \ \ \ \text{ que título de secundaria} & \\ \hline \text{Salud física} & POOR & \text{1 si es mala} & 17.2 & 10,447 \\ \ \ \text{autocalificada} & FAIR & \text{1 si es regular} & 10.2 & 5,228 \\ & GOOD & \text{1 si es buena } & 31.2 & 5,032 \\ & VGOOD & \text{1 si es muy buena} & 24.8 & 5,546 \\ && \text{Nivel de referencia es excelente salud} & 16.6 & 5,277 \\ \text{Salud mental} & MPOOR & \text{1 si es mala o regular} & 15.9 & 6,583 \\ \ \ \text{autocalificada} & & \text{0 si es buena a excelente} & 84.1 & 5,599 \\ \text{Cualquier} & ANYLIMIT & \text{1 si tiene alguna limitación funcional/de actividad} & 41.4 & 7,826 \\ \ \ \text{limitación} & & \text{0 en caso contrario} & 58.6 & 4,746 \\ \hline \text{Ingreso} && \text{Nivel de referencia es ingreso alto} & 21.7 & 7,271 \\ \text{comparado con} & MINCOME & \text{1 si es ingreso medio} & 26.8 & 5,851 \\ \text{línea de pobreza} & LINCOME & \text{1 si es ingreso bajo} & 16.6 & 6,909 \\ & NPOOR & \text{1 si es casi pobre} & 7.0 & 5,546 \\ & POORNEG & \text{si es pobre/ingreso negativo} & 28.0 & 4,097 \\ \hline \text{Seguro} & INSURE & \text{1 si tiene cobertura de salud pública/privada} & 91.1 & 5,943 \\ \ \ \text{médico} & & \ \ \text{en cualquier mes de 2003} & & \\ & & \text{0 si no tiene seguro médico en 2003} & 8.9 & 2,668 \\ \hline Total & & & 100.0 & 5,695 \\ \hline \end{array} } \]
Código R para generar la Tabla 13.5
Tabla 13.5 utiliza medianas en lugar de medias debido a que la distribución de los gastos está sesgada hacia la derecha. Esto es evidente en la Figura 13.1, que proporciona un histograma suave (conocido como “estimación de densidad por kernel”, ver Sección 15.2) para los gastos hospitalarios. Para distribuciones sesgadas, la mediana a menudo brinda una mejor idea del centro de la distribución que la media. La distribución está aún más sesgada de lo que sugiere esta figura, ya que el gasto más grande (que es $607,800) se omite en la representación gráfica.
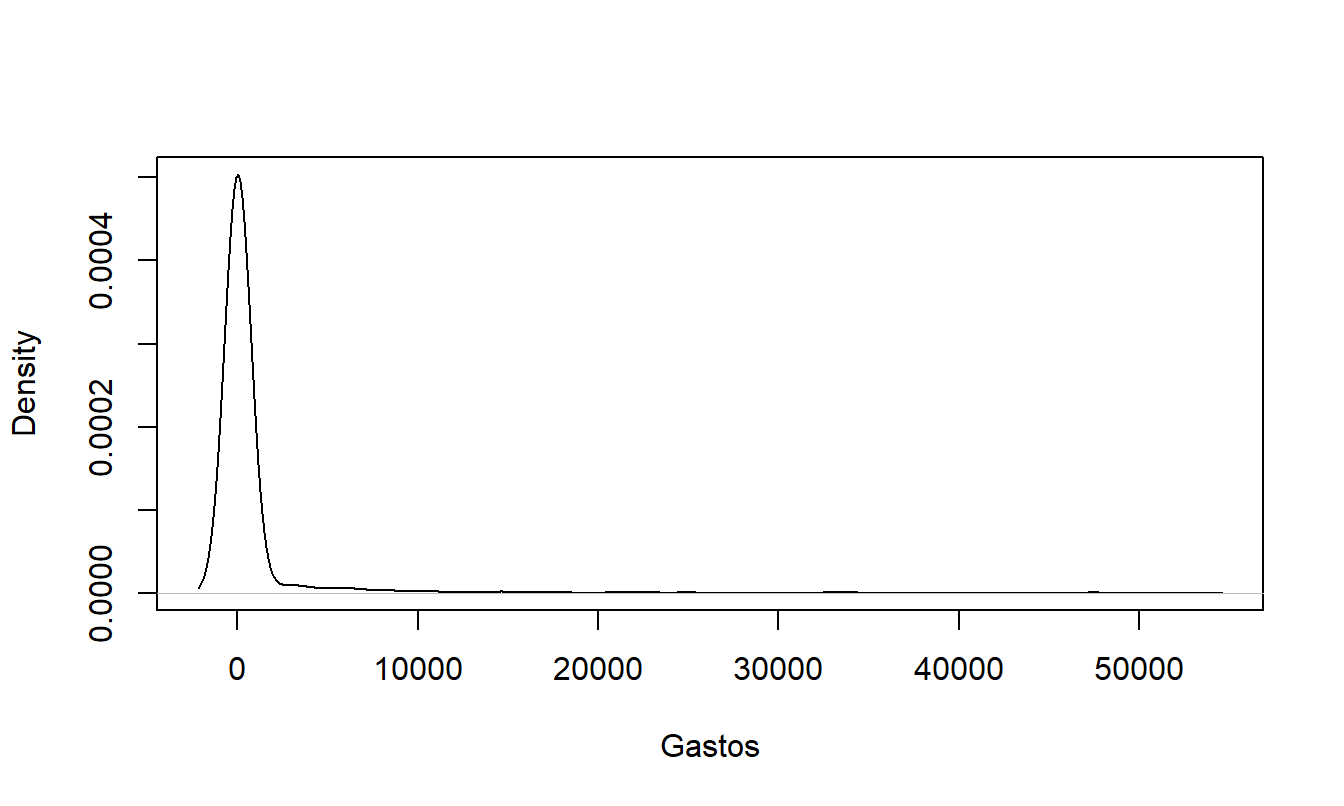
Figura 13.1: Histograma Empírico Suave de Gastos Hospitalarios Positivos. Se omite el gasto más grande.
Código R para generar la Figura 13.1
Un modelo de regresión gamma con un enlace logarítmico se ajustó a los gastos hospitalarios utilizando todas las variables explicativas. Los resultados de este ajuste de modelo aparecen en la Tabla 13.6. Aquí vemos que muchos de los posibles determinantes importantes de los gastos médicos no son estadísticamente significativos. Esto es común en el análisis de gastos, donde las variables ayudan a predecir la frecuencia, aunque no son tan útiles para explicar la severidad.
Debido a la colinealidad, hemos visto en modelos lineales que tener demasiadas variables en un modelo ajustado puede llevar a la insignificancia estadística de variables importantes e incluso causar que los signos se inviertan. Para un modelo más simple, eliminamos las variables de Asian, Native American y uninsured, ya que representan un pequeño subconjunto de nuestra muestra. También utilizamos solo la variable POOR para el estado de salud autoinformado y solo POORNEG para los ingresos, esencialmente reduciendo estas variables categóricas a variables binarias. La Tabla 13.6, bajo el encabezado “Modelo Reducido”, muestra los resultados de este ajuste del modelo. Este modelo tiene casi el mismo estadístico de bondad de ajuste, AIC, lo que sugiere que es una alternativa razonable. Bajo el ajuste del modelo reducido, las variables COUNTIP (conteo de pacientes hospitalizados), AGE, COLLEGE y POORNEG son variables estadísticamente significativas. Para estas variables significativas, los signos son intuitivamente razonables. Por ejemplo, el coeficiente positivo asociado con COUNTIP significa que a medida que aumenta el número de visitas hospitalarias, los gastos totales aumentan, como era de esperar.
Para otra especificación alternativa del modelo, la Tabla 13.6 también muestra un ajuste de un modelo inverso gaussiano con un enlace logarítmico. A partir del estadístico AIC, vemos que este modelo no se ajusta tan bien como el modelo de regresión gamma. Todas las variables son estadísticamente insignificantes, lo que dificulta la interpretación de este modelo.
Tabla 13.6. Comparación de Modelos de Regresión Gamma e Inversa Gaussiana
\[ \scriptsize{ \begin{array}{l|rr|rr|rr} \hline & \text{Gamma} & &\text{Gamma}&&\text{Inversa}&\text{Gaussiana} \\ \hline & \text{Modelo} &\text{Modelo}& \text{Modelo} & \text{Modelo}&\text{Modelo}&\text{Modelo} \\ & \text{Completo} &\text{Reducido}& \text{Completo} & \text{Reducido}&\text{Reducido}&\text{Reducido} \\ \hline & \scriptsize{Parámetro} & & \scriptsize{Parámetro} & & \scriptsize{Parámetro} & \\ \text{Efecto} & \scriptsize{Estimación} & t\text{-valor} & \scriptsize{Estimación} & t\text{-valor} & \scriptsize{Estimación} & t\text{-valor} \\ \hline Intercepto & 6.891 & 13.080 & 7.859 & 17.951 & 6.544 & 3.024 \\ COUNTIP & 0.681 & 6.155 & 0.672 & 5.965 & 1.263 & 0.989 \\ AGE & 0.021 & 3.024 & 0.015 & 2.439 & 0.018 & 0.727 \\ GENDER & -0.228 & -1.263 & -0.118 & -0.648 & 0.363 & 0.482 \\ ASIAN & -0.506 & -1.029 & & & & \\ BLACK & -0.331 & -1.656 & -0.258 & -1.287 & -0.321 & -0.577 \\ NATIVE & -1.220 & -2.217 & & & & \\ NORTHEAST & -0.372 & -1.548 & -0.214 & -0.890 & 0.109 & 0.165 \\ MIDWEST & 0.255 & 1.062 & 0.448 & 1.888 & 0.399 & 0.654 \\ SOUTH & 0.010 & 0.047 & 0.108 & 0.516 & 0.164 & 0.319 \\ \hline COLLEGE & -0.413 & -1.723 & -0.469 & -2.108 & -0.367 & -0.606 \\ HIGHSCHOOL & -0.155 & -0.827 & -0.210 & -1.138 & -0.039 & -0.078 \\ \hline POOR & -0.003 & -0.010 & 0.167 & 0.706 & 0.167 & 0.258 \\ FAIR & -0.194 & -0.641 & & & & \\ GOOD & 0.041 & 0.183 & & & & \\ VGOOD & 0.000 & 0.000 & & & & \\ MNHPOOR & -0.396 & -1.634 & -0.314 & -1.337 & -0.378 & -0.642 \\ ANYLIMIT & 0.010 & 0.053 & 0.052 & 0.266 & 0.218 & 0.287 \\ \hline MINCOME & 0.114 & 0.522 & & & & \\ LINCOME & 0.536 & 2.148 & & & & \\ NPOOR & 0.453 & 1.243 & & & & \\ POORNEG & -0.078 & -0.308 & -0.406 & -2.129 & -0.356 & -0.595 \\ INSURE & 0.794 & 3.068 & & & & \\ \hline Escala & 1.409 & 9.779 & 1.280 & 9.854 & 0.026 & 17.720 \\ \hline \scriptsize{Log-Verosimilitud} & -1,558.67 && -1,567.93 && -1,669.02 \\ AIC & 3,163.34 && 3,163.86 && 3,366.04 \\ \hline \end{array} } \]
Código R para generar la Tabla 13.6
13.5 Residuales
Una forma de seleccionar un modelo adecuado es ajustar una especificación tentativa y analizar formas de mejorarlo. Este método diagnóstico se basa en los residuales. En el modelo lineal, definimos los residuales como la respuesta menos los valores ajustados correspondientes. En un contexto de GLM, nos referimos a estos como “residuales crudos”, denotados como \(y_i - \widehat{\mu}_i\). Como hemos visto, los residuales son útiles para:
- descubrir nuevas covariables o los efectos de patrones no lineales en covariables existentes,
- identificar observaciones con mal ajuste,
- cuantificar los efectos de las observaciones individuales en los parámetros del modelo, y
- revelar otros patrones del modelo, como heterocedasticidad o tendencias temporales.
Como se enfatiza en esta sección, los residuales también son los componentes básicos de muchas estadísticas de bondad de ajuste.
Como vimos en la Sección 11.1 sobre variables dependientes binarias, el análisis de los residuales crudos puede ser irrelevante en algunos contextos no lineales. Cox y Snell (1968, 1971) introdujeron una noción general de residuales que es más útil en modelos no lineales que los simples residuales crudos. Para nuestras aplicaciones, asumimos que \(y_i\) tiene una función de distribución F(\(\cdot\)) que está indexada por las variables explicativas \(\mathbf{x}_i\) y un vector de parámetros \(\boldsymbol \theta\) denotado como F(\(\mathbf{x}_i,\boldsymbol \theta\)). Aquí, la función de distribución es común a todas las observaciones, pero la distribución varía a través de las variables explicativas. El vector de parámetros \(\boldsymbol \theta\) incluye los parámetros de regresión \(\boldsymbol \beta\) así como los parámetros de escala. Con conocimiento de F(\(\cdot\)), ahora asumimos que se puede calcular una nueva función R(\(\cdot\)) tal que \(\varepsilon_i = \mathrm{R}(y_i; \mathbf{x}_i,\boldsymbol \theta)\), donde \(\varepsilon_i\) son distribuidos idénticamente e independientemente. Aquí, la función R(\(\cdot\)) depende de las variables explicativas \(\mathbf{x}_i\) y los parámetros \(\boldsymbol \theta\). Los residuales de Cox-Snell son entonces \(e_i = \mathrm{R}(y_i; \mathbf{x}_i,\widehat{\boldsymbol \theta})\). Si el modelo está bien especificado y las estimaciones de los parámetros \(\widehat{\boldsymbol \theta}\) están cerca de los parámetros del modelo \(\boldsymbol \theta\), entonces los residuales \(e_i\) deberían estar cerca de ser i.i.d.
Para ilustrar, en el modelo lineal utilizamos la función de residuales \(\mathrm{R}(y_i; \mathbf{x}_i,\boldsymbol \theta)\) \(= y_i - \mathbf{x}_i^{\prime} \boldsymbol \beta\) \(= y_i - \mu_i = \varepsilon_i\), resultando en residuales crudos (ordinarios). Otra opción es reescalar mediante la desviación estándar \[ \mathrm{R}(y_i; \mathbf{x}_i,\boldsymbol \theta) = \frac{y_i - \mu_i}{\sqrt{\mathrm{Var~} y_i}} , \] que produce residuales de Pearson.
Otro tipo de residual se basa en transformar primero la respuesta con una función conocida h(\(\cdot\)), \[ \mathrm{R}(y_i; \mathbf{x}_i,\boldsymbol \theta) = \frac{\mathrm{h}(y_i) - \mathrm{E~} \mathrm{h}(y_i)}{\sqrt{\mathrm{Var~}\mathrm{h}(y_i)}}. \] Elegir la función de modo que h(\(y_i\)) sea aproximadamente distribuida normalmente produce residuales de Anscombe. Otra elección popular es seleccionar la transformación de modo que la varianza sea estabilizada. Tabla 13.7 presenta transformaciones para las distribuciones binomial, Poisson y gamma.
Tabla 13.7. Transformaciones Aproximadas a la Normalidad y de Estabilización de Varianza
\[ \small{ \begin{array}{lcc} \hline \text{Distribución} & \text{Transformación Aproximada } & \text{Transformación de Estabilización } \\ & \text{a la Normalidad Transformación} & \text{de Varianza Transformación} \\ \hline \text{Binomial}(m,p) & \frac{\mathrm{h}_B(y/m)-[\mathrm{h}_B(p)+(p(1-p))^{-1/3}(2p-1)/(6m)]}{(p(1-p)^{1/6}/\sqrt{m})} & \frac{\sin^{-1}(\sqrt{y/m})-\sin^{-1}(\sqrt{p})}{a/(2\sqrt{m})} \\ \text{Poisson}(\lambda) & 1.5 \lambda^{-1/6} \left[ y^{2/3}-(\lambda^{2/3}-\lambda^{-1/3}/9) \right] & 2(\sqrt{y}-\sqrt{\lambda})\\ \text{Gamma}(\alpha, \gamma) & 3 \alpha^{1/6} \left[ (y/\gamma)^{1/3}-(\alpha^{1/3}-\alpha^{-2/3}/9) \right] & \text{No considerado}\\ \hline \\ \end{array} } \] Nota: \(\mathrm{h}_B(u) = \int_0^u s^{-1/3} (1-s)^{-1/3}ds\) es la función beta incompleta evaluada en \((2/3, 2/3)\), hasta una constante escalar. Fuente: Pierce y Schafer (1986).
Otra opción ampliamente utilizada en estudios de GLM son los residuales de devianza, definidos como \[ \mathrm{sign} \left(y_i - \widehat{\mu}_i \right) \sqrt{2 \left( \ln \mathrm{f}(y_i;\theta_{i,SAT}) - \ln \mathrm{f}(y_i;\widehat{\theta}_{i}) \right)}. \] La Sección 13.3.3 introdujo las estimaciones de los parámetros del modelo saturado, \(\theta_{i,SAT}\). Como mencionan Pierce y Schafer (1986), los residuales de devianza son muy cercanos a los residuales de Anscombe en muchos casos; podemos verificar los residuales de devianza para la normalidad aproximada. Además, los residuales de devianza pueden definirse fácilmente para cualquier modelo GLM y son fáciles de calcular.
13.6 Distribución de Tweedie
Hemos visto que la familia exponencial natural incluye distribuciones continuas, como la normal y gamma, así como distribuciones discretas, como la binomial y Poisson. También incluye distribuciones que son mezclas de componentes discretos y continuos. En la modelización de reclamaciones de seguros, la mezcla más utilizada es la distribución de Tweedie (1984). Esta tiene una masa positiva en cero, representando la ausencia de reclamaciones, y un componente continuo para valores positivos que representan el monto de una reclamación.
La distribución de Tweedie se define como una suma de Poisson de variables aleatorias gamma, conocida como una pérdida agregada en ciencias actuariales. Específicamente, supongamos que \(N\) tiene una distribución de Poisson con media \(\lambda\), representando el número de reclamaciones. Sea {\(y_j\)} una secuencia i.i.d., independiente de \(N\), con cada \(y_j\) siguiendo una distribución gamma con parámetros \(\alpha\) y \(\gamma\), representando el monto de una reclamación. Entonces, \(S_N = y_1 + \ldots + y_N\) es una suma de Poisson de gammas. La Sección 16.5 discutirá con más detalle los modelos de pérdidas agregadas. Esta sección se enfoca en el caso especial importante de la distribución de Tweedie.
Para entender el aspecto de mezcla de la distribución de Tweedie, primero observa que es sencillo calcular la probabilidad de tener cero reclamaciones como \[ \Pr ( S_N=0) = \Pr (N=0) = e^{-\lambda}. \] La función de distribución puede calcularse usando expectativas condicionales, \[ \Pr ( S_N \le y) = e^{-\lambda}+\sum_{n=1}^{\infty} \Pr(N=n) \Pr(S_n \le y), ~~~~~y \geq 0. \] Dado que la suma de gammas i.i.d. es una gamma, \(S_n\) (no \(S_N\)) tiene una distribución gamma con parámetros \(n\alpha\) y \(\gamma\). Así, para \(y>0\), la densidad de la distribución de Tweedie es \[\begin{equation} \mathrm{f}_{S}(y) = \sum_{n=1}^{\infty} e^{-\lambda} \frac{\lambda ^n}{n!} \frac{\gamma^{n \alpha}}{\Gamma(n \alpha)} y^{n \alpha -1} e^{-y \gamma}. \tag{13.9} \end{equation}\]
A primera vista, esta densidad no parece pertenecer a la familia exponencial lineal dada en la ecuación (13.2). Para ver la relación, primero calculamos los momentos usando expectativas iteradas como \[\begin{equation} \mathrm{E~}S_N = \lambda \frac{\alpha}{\gamma}~~~~~~\mathrm{y}~~~~~ \mathrm{Var~}S_N = \frac{\lambda \alpha}{\gamma^2} (1+\alpha). \tag{13.10} \end{equation}\] Ahora, definimos tres parámetros \(\mu, \phi, p\) mediante las relaciones \[ \lambda = \frac{\mu^{2-p}}{\phi (2-p)},~~~~~~\alpha = \frac{2-p}{p-1}~~~~~~\mathrm{y}~~~~~ \frac{1}{\gamma} = \phi(p-1)\mu^{p-1}. \] Al insertar estos nuevos parámetros en la ecuación (13.9) obtenemos \[\begin{equation} \mathrm{f}_{S}(y) = \exp \left[ \frac{-1}{\phi} \left( \frac{\mu^{2-p}}{2-p} + \frac{y}{(p-1)\mu^{p-1}} \right) + S(y,\phi) \right]. \tag{13.11} \end{equation}\] Dejamos el cálculo de \(S(y,\phi)\) como un ejercicio.
Así, la distribución de Tweedie pertenece a la familia exponencial lineal. Cálculos sencillos muestran que \[\begin{equation} \mathrm{E~}S_N = \mu~~~~~~\mathrm{y}~~~~~ \mathrm{Var~}S_N = \phi \mu^p, \tag{13.12} \end{equation}\] donde \(1<p<2.\) Al examinar nuestra función de varianza Tabla 13.1, la distribución de Tweedie también puede verse como una elección que es intermedia entre las distribuciones Poisson y gamma.
13.7 Lecturas adicionales y referencias
Un tratamiento más extenso de los GLM puede encontrarse en el trabajo clásico de McCullagh y Nelder (1989) o la introducción más sencilla de Dobson (2002). de Jong y Heller (2008) proporcionan una reciente introducción a los GLM con un énfasis especial en seguros.
Los GLM han recibido una considerable atención de parte de los actuarios de seguros de propiedad y accidentes (generales) en los últimos tiempos. Véase Anderson et al. (2004) y Clark y Thayer (2004) para introducciones.
Mildenhall (1999) proporciona un análisis sistemático de la conexión entre los modelos GLM y los algoritmos para evaluar diferentes planes de tarificación. Fu y Wu (2008) proporcionan una versión actualizada, introduciendo una clase más amplia de algoritmos iterativos que se conectan bien con los modelos GLM.
Para más información sobre la distribución de Tweedie, consulte J{}rgensen y de Souza (1994) y Smyth y J{}rgensen (2002).
Referencias del capítulo
- Anderson, Duncan, Sholom Feldblum, Claudine Modlin, Doris Schirmacher, Ernesto Schirmacher and Neeza Thandi (2004). A practitioner’s guide to generalized linear models. Casualty Actuarial Society 2004 Discussion Papers 1-116, Casualty Actuarial Society.
- Baxter, L. A., S. M. Coutts and G. A. F. Ross (1980). Applications of linear models in motor insurance. Proceedings of the 21st International Congress of Actuaries. Zurich. pp. 11-29.
- Clark, David R. and Charles A. Thayer (2004). A primer on the exponential family of distributions. Casualty Actuarial Society 2004 Discussion Papers 117-148, Casualty Actuarial Society.
- Cox, David R. and E. J. Snell (1968). A general definition of residuals. Journal of the Royal Statistical Society, Series B, 30, 248-275.
- Cox, David R. and E. J. Snell (1971). On test statistics computed from residuals. Biometrika 71, 589-594.
- Dobson, Annette J. (2002). An Introduction to Generalized Linear Models, Second Edition. Chapman & Hall, London.
- Fu, Luyang and Cheng-sheng Peter Wu (2008). General iteration algorithm for classification ratemaking. Variance 1(2), 193-213, Casualty Actuarial Society.
- de Jong, Piet and Gillian Z. Heller (2008). Generalized Linear Models for Insurance Data. Cambridge University Press, Cambridge, UK.
- J{}rgensen, Bent and Marta C. Paes de Souza (1994). Fitting Tweedie’s compound Poisson model to insurance claims data. Scandinavian Actuarial Journal 1994;1, 69-93.
- McCullagh, P. and J.A. Nelder (1989). Generalized Linear Models, Second Edition. Chapman & Hall, London.
- Mildenhall, Stephen J. (1999). A systematic relationship between minimum bias and generalized linear models. Casualty Actuarial Society Proceedings 86, Casualty Actuarial Society.
- Pierce, Donald A. and Daniel W. Schafer (1986). Residuals in generalized linear models. Journal of the American Statistical Association 81, 977-986.
- Smyth, Gordon K. and Bent J{}rgensen (2002). Fitting Tweedie’s compound Poisson model to insurance claims data: Dispersion modelling. Astin Bulletin 32(1), 143-157.
- Tweedie, M. C. K. (1984). An index which distinguishes between some important exponential families. In Statistics: Applications and New Directions. Proceedings of the Indian Statistical Golden Jubilee International Conference* (Editors J. K. Ghosh and J. Roy), pp. 579-604. Indian Statistical Institute, Calcutta.
13.8 Ejercicios
13.1 Verifica las entradas en Tabla 13.8 para la distribución gamma. Específicamente:
Demuestra que la distribución gamma es un miembro de la familia exponencial lineal de distribuciones.
Describe los componentes de la familia exponencial lineal (\(\theta, \phi, b(\theta), S(y,\phi)\)) en términos de los parámetros de la distribución gamma.
Demuestra que la media y la varianza de la distribución gamma y de las distribuciones de la familia exponencial lineal coinciden.
13.2 Clasificación de Tarificación. Este ejercicio considera los datos descritos en el ejemplo de clasificación de tarificación de la Sección 13.2.2, utilizando los datos de la Tabla 13.3.
Ajusta un modelo de regresión gamma usando una función de enlace logarítmica con los conteos de reclamaciones como ponderaciones (\(w_i\)). Utiliza las variables explicativas categóricas de grupo de edad y uso del vehículo para estimar la severidad media esperada.
Con base en tus parámetros estimados en la parte (a), verifica las severidades esperadas estimadas en la Tabla 13.4.
13.3 Verifica que la distribución de Tweedie es un miembro de la familia exponencial lineal de distribuciones comprobando la ecuación (13.9). En particular, proporciona una expresión para \(S(y,\phi)\) (nota que \(S(y,\phi)\) también depende de \(p\) pero no de \(\mu\)). Puedes consultar a Clark y Thayer (2004) para verificar tu trabajo. Además, verifica los momentos en la ecuación (13.10).
13.9 Suplementos Técnicos - Familia Exponencial
13.9.1 Familia Exponencial Lineal de Distribuciones
La distribución de la variable aleatoria \(y\) puede ser discreta, continua o una mezcla. Así, f(.) en la ecuación (13.2) puede interpretarse como una función de densidad o una función de masa, dependiendo de la aplicación. Tabla 13.8 proporciona varios ejemplos, incluyendo las distribuciones normal, binomial y Poisson.
Tabla 13.8. Distribuciones Seleccionadas de la Familia Exponencial de Un Parámetro
\[ \scriptsize{ \begin{array}{l|ccccc} \hline & & \text{Densidad o} & & & \\ \text{Distribución} & \text{Parámetros} & \text{Función de Masa} & \text{Componentes} & \mathrm{E}~y & \mathrm{Var}~y \\ \hline \text{General} & \theta,~ \phi & \exp \left( \frac{y\theta -b(\theta )}{\phi } +S\left( y,\phi \right) \right) & \theta,~ \phi, b(\theta), S(y, \phi) & b^{\prime}(\theta) & b^{\prime \prime}(\theta) \phi \\ \text{Normal} & \mu, \sigma^2 & \frac{1}{\sigma \sqrt{2\pi }}\exp \left( -\frac{(y-\mu )^{2}}{2\sigma ^{2}}\right) & \mu, \sigma^2, \frac{\theta^2}{2}, - \left(\frac{y^2}{2\phi} + \frac{\ln(2 \pi \phi)}{2} \right) & \theta=\mu & \phi= \sigma^2 \\ \text{Binomial} & \pi & {n \choose y} \pi ^y (1-\pi)^{n-y} & \ln \left(\frac{\pi}{1-\pi} \right), 1, n \ln(1+e^{\theta} ), & n \frac {e^{\theta}}{1+e^{\theta}} & n \frac {e^{\theta}}{(1+e^{\theta})^2} \\ & & & \ln {n \choose y} & = n \pi & = n \pi (1-\pi) \\ \text{Poisson} & \lambda & \frac{\lambda^y}{y!} \exp(-\lambda) & \ln \lambda, 1, e^{\theta}, - \ln (y!) & e^{\theta} = \lambda & e^{\theta} = \lambda \\ \text{Negativa} & r,p & \frac{\Gamma(y+r)}{y! \Gamma(r)} p^r ( 1-p)^y & \ln(1-p), 1, -r \ln(1-e^{\theta}), & \frac{r(1-p)}{p} & \frac{r(1-p)}{p^2} \\ \ \ \ \text{Binomial}^{\ast} & & & ~~~\ln \left[ \frac{\Gamma(y+r)}{y! \Gamma(r)} \right] & = \mu & = \mu+\mu^2/r \\ \text{Gamma} & \alpha, \gamma & \frac{\gamma ^ \alpha}{\Gamma (\alpha)} y^{\alpha -1 }\exp(-y \gamma) & - \frac{\gamma}{\alpha}, \frac{1}{\alpha}, - \ln ( - \theta), -\phi^{-1} \ln \phi & - \frac{1}{\theta} = \frac{\alpha}{\gamma} & \frac{\phi}{\theta ^2} = \frac{\alpha}{\gamma ^2} \\ & & & - \ln \left( \Gamma(\phi ^{-1}) \right) + (\phi^{-1} - 1) \ln y & & \\ \text{Inversa} & \mu, \lambda & \sqrt{\frac{\lambda}{2 \pi y^3} } \exp \left(- \frac{\lambda (y-\mu)^2}{2 \mu^2 y} \right) & -1/( 2\mu^2), 1/\lambda, -\sqrt{-2 \theta}, & \left(-2 \theta \right)^{-1/2} & \phi (-2 \theta)^{-3/2} \\ \ \ \ \text{Gaussiana} & & & \theta/(\phi y) - 0.5 \ln (\phi 2 \pi y^3 ) & = \mu & = \frac{\mu^3}{\lambda} \\ \text{Tweedie} & & \textit{Ver Sección 13.6}\\ \hline \\ \end{array} } \] \(^{\ast}\) Esto supone que el parámetro \(r\) es fijo, pero no tiene que ser un número entero.
13.9.2 Momentos
Para evaluar los momentos de las familias exponenciales, es conveniente trabajar con la función generadora de momentos. Para simplificar, asumimos que la variable aleatoria \(y\) es continua. Definimos la función generadora de momentos
\[\begin{eqnarray*} M(s) &=& \mathrm{E}~ e^{sy} = \int \exp \left( sy+ \frac{y \theta - b(\theta)}{\phi} + S(y, \phi) \right) dy \\ &=& \exp \left(\frac{b(\theta + s \phi) - b(\theta)}{\phi} \right) \int \exp \left( \frac{y(\theta + s\phi) - b(\theta+s\phi)}{\phi} + S(y, \phi) \right) dy \\ &=& \exp \left(\frac{b(\theta + s \phi) - b(\theta)}{\phi} \right), \end{eqnarray*}\] porque \(\int \exp \left( \frac{1}{\phi} \left[ y(\theta + s\phi) - b(\theta+s\phi) \right] + S(y, \phi) \right) dy=1\). Con esta expresión, podemos generar los momentos. Así, para la media, tenemos \[\begin{eqnarray*} \mathrm{E}~ y &=& M^{\prime}(0) = \left . \frac{\partial}{\partial s} \exp \left(\frac{b(\theta + s \phi) - b(\theta)}{\phi} \right) \right | _{s=0} \\ &=& \left[ b^{\prime}(\theta + s \phi ) \exp \left( \frac{b(\theta + s \phi) - b(\theta)}{\phi} \right) \right] _{s=0} = b^{\prime}(\theta). \end{eqnarray*}\]
De manera similar, para el segundo momento, tenemos \[\begin{eqnarray*} M^{\prime \prime}(s) &=& \frac{\partial}{\partial s} \left[ b^{\prime}(\theta + s \phi) \exp \left(\frac{b(\theta + s \phi) - b(\theta)}{\phi} \right) \right] \\ &=& \phi b^{\prime \prime}(\theta + s \phi) \exp \left(\frac{b(\theta + s \phi) - b(\theta)}{\phi} \right) + (b^{\prime}(\theta + s \phi))^2 \left(\frac{b(\theta + s \phi) - b(\theta)}{\phi} \right). \end{eqnarray*}\] Esto produce \(\mathrm{E}y^2 = M^{\prime \prime}(0)\) \(= \phi b^{\prime \prime}(\theta) + (b^{\prime}(\theta))^2\) y \(\mathrm{Var}~y =\phi b^{\prime \prime}(\theta)\).
13.9.3 Estimación de Máxima Verosimilitud para Enlaces Generales
Para enlaces generales, ya no asumimos la relación \(\theta_i=\mathbf{x}_i^{\mathbf{\prime }}\boldsymbol \beta\), sino que asumimos que \(\boldsymbol \beta\) está relacionado con \(\theta_i\) a través de las relaciones \(\mu _i=b^{\prime }(\theta_i)\) y \(\mathbf{x}_i^{\mathbf{\prime }}\boldsymbol \beta = g\left( \mu _i\right)\). Seguimos asumiendo que el parámetro de escala varía según la observación, de modo que \(\phi_i = \phi/w_i\), donde \(w_i\) es una función de ponderación conocida. Usando la ecuación (13.4), tenemos que el \(j\)-ésimo elemento de la función de puntaje es \[ \frac{\partial }{\partial \beta _{j}}\ln \mathrm{f}\left( \mathbf{y}\right) =\sum_{i=1}^n \frac{\partial \theta_i}{\partial \beta _{j}} \frac{y_i-\mu _i}{\phi _i}, \] ya que \(b^{\prime }(\theta_i)=\mu _i\). Ahora, usamos la regla de la cadena y la relación \(\mathrm{Var~}y_i=\phi _ib^{\prime \prime }(\theta_i)\) para obtener \[ \frac{\partial \mu _i}{\partial \beta _{j}}=\frac{\partial b^{\prime }(\theta_i)}{\partial \beta _{j}}=b^{\prime \prime }(\theta_i)\frac{ \partial \theta_i}{\partial \beta _{j}}=\frac{\mathrm{Var~}y_i}{\phi _i}\frac{\partial \theta_i}{\partial \beta _{j}}. \] Así, tenemos \[ \frac{\partial \theta_i}{\partial \beta _{j}}\frac{1}{\phi _i}=\frac{\partial \mu _i}{\partial \beta _{j}}\frac{1}{\mathrm{Var~}y_i}. \] Esto produce \[ \frac{\partial }{\partial \beta _{j}}\ln \mathrm{f}\left( \mathbf{y}\right) =\sum_{i=1}^n \frac{\partial \mu _i}{\partial \beta _{j}}\left( \mathrm{Var~}y_i\right) ^{-1}\left( y_i-\mu _i\right), \] que resumimos como \[\begin{equation} \frac{\partial L(\boldsymbol \beta) }{\partial \boldsymbol \beta } = \frac{\partial }{\partial \boldsymbol \beta }\ln \mathrm{f}\left( \mathbf{y}\right) =\sum_{i=1}^n \frac{\partial \mu _i}{\partial \boldsymbol \beta}\left( \mathrm{Var~}y_i\right) ^{-1}\left( y_i-\mu _i\right), \tag{13.13} \end{equation}\] que se conoce como la forma de las ecuaciones de estimación generalizadas.
Resolver las raíces de la ecuación de puntaje \(L(\boldsymbol \beta) = \mathbf{0}\) proporciona estimaciones de máxima verosimilitud, \(\mathbf{b}_{MLE}\). En general, esto requiere métodos numéricos iterativos. Una excepción es el siguiente caso especial.
Caso especial. Sin covariables. Supongamos que \(k=1\) y que \(x_i =1\). Entonces, \(\beta = \eta = g(\mu)\), y \(\mu\) no depende de \(i\). A partir de la relación \(\mathrm{Var~}y_i = \phi b^{\prime \prime}(\theta)/w_i\) y la ecuación (13.13), la función de puntaje es \[ \frac{\partial L( \beta) }{\partial \beta } = \frac{\partial \mu}{\partial \beta} ~ \frac{1}{\phi b^{\prime \prime}(\theta)} \sum_{i=1}^n w_i \left( y_i-\mu \right). \] Igualando esto a cero se obtiene \(\overline{y}_w = \sum_i w_i y_i / \sum_i w_i = \widehat{\mu}_{MLE} = g^{-1}(b_{MLE})\), o \(b_{MLE}=g(\overline{y}_w)\), donde \(\overline{y}_w\) es un promedio ponderado de los \(y\).
Para la matriz de información, usamos la independencia entre los sujetos y la ecuación (13.13) para obtener \[\begin{eqnarray} \mathbf{I}(\boldsymbol \beta) &=& \mathrm{E~} \left( \frac{\partial L(\boldsymbol \beta) }{\partial \boldsymbol \beta } \frac{\partial L(\boldsymbol \beta) }{\partial \boldsymbol \beta ^{\prime}} \right) \nonumber \\ &=& \sum_{i=1}^n \frac{\partial \mu _i}{\partial \boldsymbol \beta}~\mathrm{E} \left( \left( \mathrm{Var~}y_i\right) ^{-1}\left( y_i-\mu _i\right)^2 \left( \mathrm{Var~}y_i\right) ^{-1}\right) \frac{\partial \mu _i}{\partial \boldsymbol \beta ^{\prime}} \nonumber \\ &=& \sum_{i=1}^n \frac{\partial \mu _i}{\partial \boldsymbol \beta} \left( \mathrm{Var~}y_i\right) ^{-1} \frac{\partial \mu _i}{\partial \boldsymbol \beta ^{\prime}} . \tag{13.14} \end{eqnarray}\]
Tomar la raíz cuadrada de los elementos diagonales de la inversa de \(\mathbf{I}(\boldsymbol \beta)\), después de insertar las estimaciones de los parámetros en las funciones de media y varianza, proporciona errores estándar basados en el modelo. Para datos en los que se duda de la correcta especificación del componente de varianza, se reemplaza Var \(y_i\) por una estimación insesgada \((y_i - \mu_i)^2\). El estimador resultante \[ se(b_j) = \sqrt{ j\text{-ésimo elemento diagonal de } [\sum_{i=1}^n \frac{\partial \mu _i}{\partial \boldsymbol \beta} (y_i - \mu_i)^{-2} \frac{\partial \mu _i}{\partial \boldsymbol \beta ^{\prime}}]|_{\boldsymbol \beta = \mathbf{b}_{MLE}}^{-1}} \]
se conoce como el error estándar empírico o robusto.
13.9.4 Mínimos Cuadrados Reponderados Iterativos
Para ver cómo funcionan los métodos iterativos generales, usamos el enlace canónico de modo que \(\eta_i = \theta_i\). Luego, la función de puntaje está dada en la ecuación (13.6) y el Hessiano en la ecuación (13.8). Usando la ecuación de Newton-Raphson (11.15) en la Sección 11.9 obtenemos \[\begin{equation} \boldsymbol \beta_{NEW} = \boldsymbol \beta_{OLD} - \left( \sum_{i=1}^n w_i b^{\prime \prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta _{OLD}) \mathbf{x}_i \mathbf{x}_i^{\prime} \right)^{-1} \left( \sum_{i=1}^n w_i (y_i - b^{\prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta_{OLD})) \mathbf{x}_i \right). \tag{13.15} \end{equation}\] Observa que, dado que la matriz de segundas derivadas no es estocástica, Newton-Raphson es equivalente al algoritmo de puntuación de Fisher. Como se describe en la Sección 13.3.1, la estimación de \(\boldsymbol \beta\) no requiere el conocimiento de \(\phi\).
Seguimos usando el enlace canónico y definimos una “variable dependiente ajustada” \[ y_i^{\ast}(\boldsymbol \beta) = \mathbf{x}_i^{\prime} \boldsymbol \beta + \frac{y_i - b^{\prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta)}{b^{\prime \prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta)}. \] Esto tiene varianza \[ \mathrm{Var~}y_i^{\ast}(\boldsymbol \beta) = \frac{\mathrm{Var~}y_i}{(b^{\prime \prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta))^2} = \frac{\phi_i b^{\prime \prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta)}{(b^{\prime \prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta))^2} = \frac{\phi/ w_i }{b^{\prime \prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta)}. \] Usamos el nuevo peso como el recíproco de la varianza, \(w_i(\boldsymbol \beta)=w_i b^{\prime \prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta) / \phi.\) Luego, con la expresión \[ w_i \left(y_i - b^{\prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta)\right) = w_i b^{\prime \prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta) (y_i^{\ast}(\boldsymbol \beta) - \mathbf{x}_i^{\prime} \boldsymbol \beta) = \phi w_i(\boldsymbol \beta) (y_i^{\ast}(\boldsymbol \beta) - \mathbf{x}_i^{\prime} \boldsymbol \beta), \] a partir de la iteración de Newton-Raphson en la ecuación (13.15), tenemos
\(\boldsymbol \beta_{NEW}\) \[\begin{eqnarray*} ~ &=& \boldsymbol \beta_{OLD} - \left( \sum_{i=1}^n w_i b^{\prime \prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta _{OLD}) \mathbf{x}_i \mathbf{x}_i^{\prime} \right)^{-1} \left( \sum_{i=1}^n w_i (y_i - b^{\prime}(\mathbf{x}_i^{\prime} \boldsymbol \beta_{OLD})) \mathbf{x}_i \right) \\ &=& \boldsymbol \beta_{OLD} - \left( \sum_{i=1}^n \phi w_i(\boldsymbol \beta _{OLD}) \mathbf{x}_i \mathbf{x}_i^{\prime} \right)^{-1} \left( \sum_{i=1}^n \phi w_i(\boldsymbol \beta _{OLD}) (y_i^{\ast}(\boldsymbol \beta_{OLD}) - \mathbf{x}_i^{\prime} \boldsymbol \beta_{OLD})\mathbf{x}_i \right) \\ &=& \boldsymbol \beta_{OLD} - \left( \sum_{i=1}^n w_i(\boldsymbol \beta _{OLD}) \mathbf{x}_i \mathbf{x}_i^{\prime} \right)^{-1} \left( \sum_{i=1}^n w_i(\boldsymbol \beta _{OLD})\mathbf{x}_i y_i^{\ast}(\boldsymbol \beta_{OLD}) - \sum_{i=1}^n w_i(\boldsymbol \beta _{OLD})\mathbf{x}_i \mathbf{x}_i^{\prime} \boldsymbol \beta_{OLD}) \right) \\ &=& \left( \sum_{i=1}^n w_i(\boldsymbol \beta _{OLD}) \mathbf{x}_i \mathbf{x}_i^{\prime} \right)^{-1} \left( \sum_{i=1}^n w_i(\boldsymbol \beta _{OLD})\mathbf{x}_i y_i^{\ast}(\boldsymbol \beta_{OLD}) \right). \end{eqnarray*}\] Así, esto proporciona un método para la iteración usando mínimos cuadrados ponderados. Los mínimos cuadrados reponderados iterativos también están disponibles para enlaces generales utilizando la puntuación de Fisher. Ver McCullagh y Nelder (1989) para más detalles.