Chapter 5 Selección de Variables

Vista previa del capítulo. Este capítulo describe herramientas y técnicas para ayudar a seleccionar las variables a incluir en un modelo de regresión lineal, comenzando con un proceso iterativo de selección de modelos. En aplicaciones con muchas variables explicativas potenciales, los procedimientos automáticos de selección de variables ayudan a evaluar rápidamente muchos modelos. Sin embargo, los procedimientos automáticos tienen serias limitaciones, incluida la incapacidad de manejar adecuadamente las no linealidades como el impacto de puntos inusuales; este capítulo amplía la discusión del Capítulo 2 sobre puntos inusuales. También se describe la colinealidad, una característica común de los datos de regresión donde las variables explicativas están linealmente relacionadas entre sí. Otros temas que afectan la selección de variables, como la heterocedasticidad y la validación fuera de muestra, también se introducen.

5.1 Un Enfoque Iterativo para el Análisis de Datos y Modelado

En nuestra introducción a la regresión lineal básica en el Capítulo 2, examinamos los datos gráficamente, formulamos una hipótesis sobre la estructura del modelo y comparamos los datos con un modelo candidato para formular un modelo mejorado. Box (1980) describe esto como un proceso iterativo, que se muestra en la Figura 5.1.

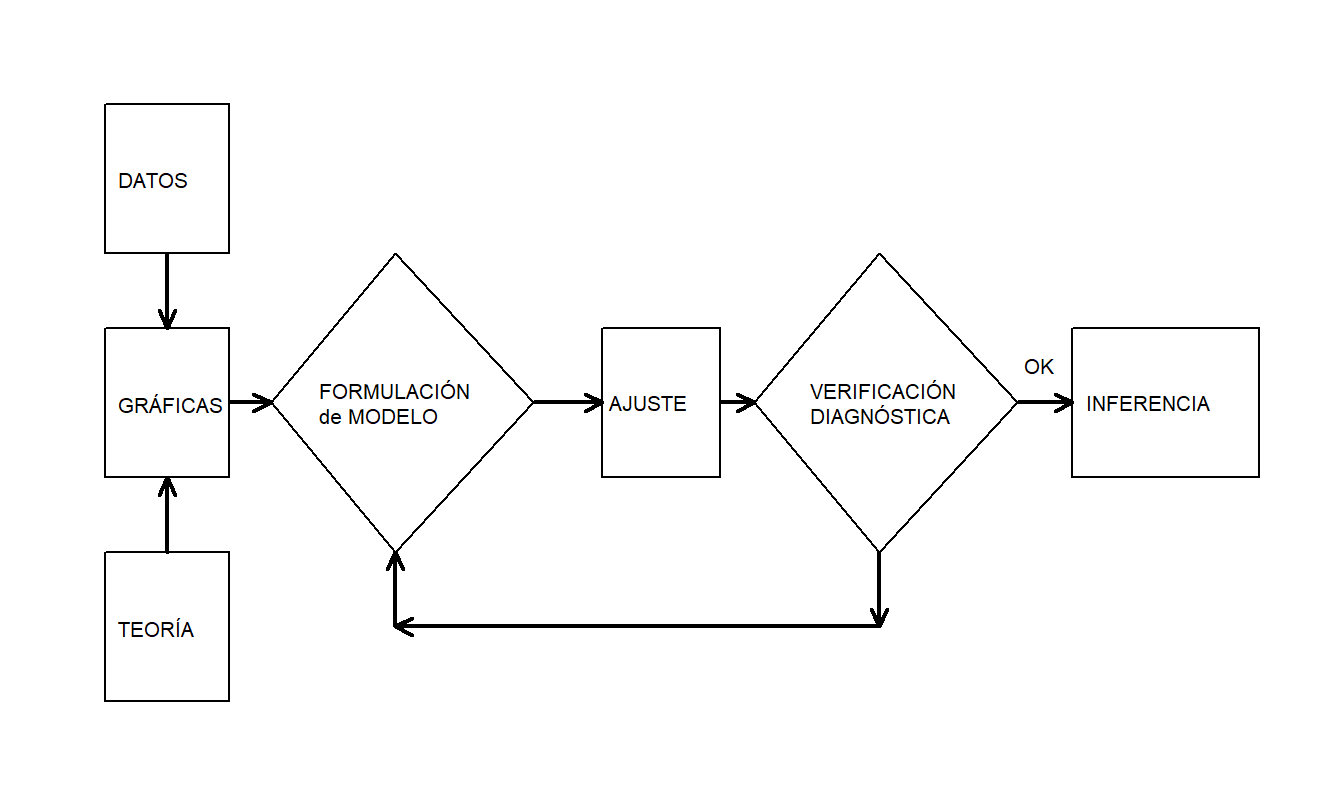
Figura 5.1: El proceso iterativo de especificación del modelo

Este proceso iterativo proporciona una receta útil para estructurar la tarea de especificar un modelo que represente un conjunto de datos. El primer paso, la etapa de formulación del modelo, se realiza examinando los datos gráficamente y utilizando el conocimiento previo de las relaciones, como de la teoría económica o de la práctica estándar de la industria. El segundo paso en la iteración se basa en los supuestos del modelo especificado. Estos supuestos deben ser consistentes con los datos para hacer un uso válido del modelo. El tercer paso, verificación diagnóstica, también se conoce como crítica de datos y modelo; los datos y el modelo deben ser consistentes entre sí antes de que se puedan hacer inferencias adicionales. La verificación diagnóstica es una parte importante de la formulación del modelo; puede revelar errores cometidos en pasos anteriores y proporcionar formas de corregir estos errores.

5.2 Procedimientos Automáticos de Selección de Variables

Las relaciones en negocios y economía son complicadas; típicamente hay muchas variables que podrían servir como predictores útiles de la variable dependiente. Al buscar una relación adecuada, hay una gran cantidad de modelos potenciales que se basan en combinaciones lineales de variables explicativas y un número infinito de modelos que pueden formarse a partir de combinaciones no lineales. Para buscar entre los modelos basados en combinaciones lineales, existen varios procedimientos automáticos para seleccionar las variables que se incluirán en el modelo. Estos procedimientos automáticos son fáciles de usar y sugerirán uno o más modelos que se pueden explorar con mayor detalle.

Para ilustrar cuán grande es el número potencial de modelos lineales, supongamos que solo hay cuatro variables, $x_{1}, x_2, x_3$ y $x_4$, bajo consideración para ajustar un modelo a $y$. Sin considerar la multiplicación u otras combinaciones no lineales de las variables explicativas, ¿cuántos modelos posibles hay? La Tabla 5.1 muestra que la respuesta es 16.

Tabla 5.1: **Dieciséis Modelos Posibles**
Expression	Combinations	Models
E $y=\beta_0$		1 modelo sin variables independientes
E $y=\beta_0+\beta_1x_i$	$i$ = 1,2,3,4	4 modelos con una variable independiente
E $y = \beta_0 + \beta_1 x_i + \beta_2 x_j$	($i,j$) = (1,2),(1,3),(1,4),(2,3),(2,4),(3,4)	6 modelos con dos variables independientes
E $y = \beta_0 + \beta_1 x_1 + \beta_2 x_j +\beta_3x_{k}$	($i,j,k$) = (1,2,3),(1,2,4),(1,3,4),(2,3,4)	4 modelos con tres variables independientes
E $y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 +\beta_3 x_3 + \beta_4 x_4$		1 modelo con todas las variables independientes

Si solo hubiera tres variables explicativas, entonces se puede usar la misma lógica para verificar que hay ocho modelos posibles. Extrapolando a partir de estos dos ejemplos, ¿cuántos modelos lineales habrá si hay diez variables explicativas? La respuesta es 1,024, lo cual es bastante. En general, la respuesta es $2^k$, donde $k$ es el número de variables explicativas. Por ejemplo, $2^3$ es 8, $2^4$ es 16, y así sucesivamente.

En cualquier caso, para un número moderadamente grande de variables explicativas, hay muchos modelos potenciales que se basan en combinaciones lineales de variables explicativas. Nos gustaría tener un procedimiento para buscar rápidamente entre estos modelos potenciales y darnos más tiempo para pensar en otros aspectos interesantes de la selección de modelos. La regresión por pasos son procedimientos que emplean pruebas $t$ para verificar la “significancia” de las variables explicativas que se incluyen o eliminan del modelo.

Para comenzar, en la versión de selección hacia adelante de la regresión por pasos, las variables se agregan una a la vez. En la primera etapa, de todas las variables candidatas, se agrega al modelo la que es más estadísticamente significativa. En la siguiente etapa, con la variable de la primera etapa ya incluida, se agrega la siguiente variable más estadísticamente significativa. Este procedimiento se repite hasta que se hayan agregado todas las variables estadísticamente significativas. Aquí, la significancia estadística generalmente se evalúa utilizando el cociente $t$ de una variable; el umbral para la significancia estadística es típicamente un valor $t$ predefinido (como dos, que corresponde a un nivel de significancia aproximado del 95%).

La versión de selección hacia atrás funciona de manera similar, excepto que todas las variables se incluyen en la etapa inicial y luego se eliminan una a la vez (en lugar de agregarse).

Más generalmente, un algoritmo que agrega y elimina variables en cada etapa a veces se conoce como el algoritmo de regresión por pasos.

Algoritmo de Regresión por Pasos. Suponga que el analista ha identificado una variable como la respuesta, $y$, y $k$ variables explicativas potenciales, $x_1, x_2, \ldots, x_k$.

Considere todas las regresiones posibles usando una variable explicativa. Para cada una de las $k$ regresiones, calcule $t(b_1)$, el cociente $t$ para la pendiente. Elija la variable con el cociente $t$ más grande. Si el cociente $t$ no supera un valor $t$ predefinido (como dos), entonces no elija ninguna variable y detenga el procedimiento.
Agregue una variable al modelo del paso anterior. La variable a ingresar es la que hace la contribución más significativa. Para determinar el tamaño de la contribución, use el valor absoluto del cociente $t$ de la variable. Para ingresar, el cociente $t$ debe superar un valor $t$ especificado en valor absoluto.
Elimine una variable del modelo del paso anterior. La variable a eliminar es la que hace la menor contribución. Para determinar el tamaño de la contribución, use el valor absoluto del cociente $t$ de la variable. Para ser eliminada, el cociente $t$ debe ser menor que un valor $t$ especificado en valor absoluto.
Repita los pasos (ii) y (iii) hasta que se realicen todas las posibles adiciones y eliminaciones.

Al implementar esta rutina, algunos paquetes de software estadístico usan una prueba $F$ en lugar de pruebas $t$. Recuerde que, cuando solo se considera una variable, $(t\text{-cociente})^2 = F$-cociente, y por lo tanto, estos procedimientos son equivalentes.

Este algoritmo es útil porque busca rápidamente entre varios modelos candidatos. Sin embargo, presenta varias desventajas:

El procedimiento “husmea” entre un gran número de modelos y puede ajustar los datos “demasiado bien.”
No hay garantía de que el modelo seleccionado sea el mejor. El algoritmo no considera modelos que se basan en combinaciones no lineales de variables explicativas. También ignora la presencia de valores atípicos y puntos de alta influencia.
Además, el algoritmo no busca todos los $2^{k}$ regresiones lineales posibles.
El algoritmo utiliza un criterio, un cociente $t$, y no considera otros criterios como $s$, $R^2$, $R_a^2$, y así sucesivamente.
Hay una secuencia de pruebas de significancia involucradas. Por lo tanto, el nivel de significancia que determina el valor $t$ no es significativo.
Al considerar cada variable por separado, el algoritmo no toma en cuenta el efecto conjunto de las variables explicativas.
Los procedimientos puramente automáticos pueden no tener en cuenta el conocimiento especial de un investigador.

Muchas de las críticas al algoritmo básico de regresión paso a paso pueden abordarse con software de computación moderno que ahora está ampliamente disponible. Ahora consideraremos cada inconveniente, en orden inverso. Para responder a la desventaja número (7), muchas rutinas de software estadístico tienen opciones para forzar la inclusión de variables en una ecuación de modelo. De esta manera, si otras evidencias indican que una o más variables deben incluirse en el modelo, el investigador puede forzar la inclusión de estas variables.

Para la desventaja número (6), en la Sección 5.5.4 sobre variables supresoras, proporcionaremos ejemplos de variables que no tienen efectos individuales importantes pero son importantes cuando se consideran en conjunto. Estas combinaciones de variables pueden no ser detectadas con el algoritmo básico, pero serán detectadas con el algoritmo de selección hacia atrás. Dado que el procedimiento de selección hacia atrás comienza con todas las variables, detectará y conservará las variables que son importantes en conjunto.

La desventaja número (5) es realmente una sugerencia sobre la forma de utilizar la regresión paso a paso. Bendel y Afifi (1977) sugirieron usar un valor de corte más pequeño del que normalmente se usaría. Por ejemplo, en lugar de usar un $t$-valor = 2 que corresponde aproximadamente a un nivel de significancia del 5%, considere usar un $t$-valor = 1.645 que corresponde aproximadamente a un nivel de significancia del 10%. De esta manera, hay menos posibilidad de excluir variables que pueden ser importantes. Un límite inferior, pero aún una buena opción para trabajo exploratorio, es un corte tan pequeño como $t$-valor = 1. Esta elección está motivada por un resultado algebraico: cuando una variable entra en un modelo, $s$ disminuirá si el $t$-ratio excede uno en valor absoluto.

Para abordar las desventajas número (3) y (4), ahora introducimos la rutina de mejores regresiones. Las mejores regresiones es un algoritmo útil que ahora está ampliamente disponible en paquetes de software estadístico. El algoritmo de mejor regresión busca en todas las combinaciones posibles de variables explicativas, a diferencia de la regresión paso a paso, que agrega y elimina una variable a la vez. Por ejemplo, suponga que hay cuatro posibles variables explicativas, $x_1$, $x_2$, $x_3$ y $x_4$, y el usuario desea saber cuál es el mejor modelo de dos variables. El algoritmo de mejor regresión busca entre los seis modelos de la forma $\mathrm{E}~y = \beta_0 + \beta_1 x_i + \beta_2 x_j$. Típicamente, una rutina de mejor regresión recomienda uno o dos modelos para cada modelo con coeficiente $p$, donde p es un número especificado por el usuario. Debido a que se ha especificado el número de coeficientes que entrarán en el modelo, no importa qué criterio usemos: $R^2$, $R_a^2$ o $s$.

El algoritmo de mejor regresión realiza su búsqueda mediante un uso ingenioso del hecho algebraico de que, cuando se añade una variable al modelo, la suma de cuadrados del error no aumenta. Debido a este hecho, ciertas combinaciones de variables incluidas en el modelo no necesitan ser calculadas. Un inconveniente importante de este algoritmo es que puede tomar mucho tiempo cuando el número de variables consideradas es grande.

Los usuarios de la regresión no siempre aprecian la profundidad del inconveniente número (1), data-snooping (exploración de datos). La exploración de datos ocurre cuando el analista ajusta un gran número de modelos a un conjunto de datos. Abordaremos el problema de la exploración de datos en la Sección 5.6.2 sobre validación de modelos. Aquí, ilustraremos el efecto de la exploración de datos en la regresión paso a paso.

Ejemplo: Exploración de Datos en Regresión Paso a Paso. La idea de esta ilustración es de Rencher y Pun (1980). Considere $n = 100$ observaciones de $y$ y cincuenta variables explicativas, $x_1, x_2, \ldots, x_{50}$. Los datos que consideramos aquí se simularon usando variables aleatorias normales estándar independientes. Debido a que las variables se simularon de manera independiente, estamos trabajando bajo la hipótesis nula de que no hay relación entre la respuesta y las variables explicativas, es decir, $H_0: \beta_1 = \beta_2 = \ldots = \beta_{50} = 0$. De hecho, cuando se ajustó el modelo con las cincuenta variables explicativas, resultó que $s = 1.142$, $R^2 = 46.2\%$, y el $F$-ratio = $\frac{Regression~MS}{Error~MS} = 0.84$. Usando una distribución $F$ con $df_1 = 50$ y $df_2 = 49$, el percentil 95 es 1.604. De hecho, 0.84 es el percentil 27 de esta distribución, lo que indica que el valor $p$ es 0.73. Por lo tanto, como era de esperar, los datos están en congruencia con $H_0$.

A continuación, se realizó una regresión paso a paso con $t$-valor = 2. Dos variables fueron retenidas por este procedimiento, lo que resultó en un modelo con $s = 1.05$, $R^2 = 9.5\%$ y $F$-ratio = 5.09. Para una distribución $F$ con $df_1 = 2$ y $df_2 = 97$, el percentil 95 es un $F$-valor = 3.09. Esto indica que las dos variables son predictores estadísticamente significativos de $y$. A primera vista, este resultado es sorprendente. Los datos se generaron de manera que $y$ no estuviera relacionado con las variables explicativas. Sin embargo, debido a que $F$-ratio $>$ $F$-valor, la prueba $F$ indica que dos variables explicativas están significativamente relacionadas con $y$. La razón es que la regresión paso a paso ha realizado muchas pruebas de hipótesis en los datos. Por ejemplo, en el Paso 1, se realizaron cincuenta pruebas para encontrar variables significativas. Recuerde que un nivel del 5% significa que esperamos cometer aproximadamente un error en 20. Por lo tanto, con cincuenta pruebas, esperamos encontrar $50 \times 0.05 = 2.5$ variables “significativas”, incluso bajo la hipótesis nula de que no hay relación entre $y$ y las variables explicativas.

Para continuar, se realizó una regresión paso a paso con $t$-valor = 1.645. Seis variables fueron retenidas por este procedimiento, lo que resultó en un modelo con $s = 0.99$, $R^2 = 22.9\%$ y $F$-ratio = 4.61. Como antes, una prueba $F$ indica una relación significativa entre la respuesta y estas seis variables explicativas.

Para resumir, utilizando simulación, construimos un conjunto de datos de manera que las variables explicativas no tuvieran relación con la respuesta. Sin embargo, al utilizar la regresión paso a paso para examinar los datos, “encontramos” relaciones aparentemente significativas entre la respuesta y ciertos subconjuntos de las variables explicativas. Este ejemplo ilustra una advertencia general en la selección de modelos: cuando las variables explicativas se seleccionan utilizando los datos, los $t$-ratios y los $F$-ratios serán demasiado grandes, exagerando así la importancia de las variables en el modelo.

La regresión paso a paso y las mejores regresiones son ejemplos de procedimientos automáticos de selección de variables. En su trabajo de modelado, encontrará que estos procedimientos son útiles porque pueden buscar rápidamente entre varios modelos candidatos. Sin embargo, estos procedimientos ignoran alternativas no lineales, así como el efecto de los valores atípicos y los puntos de alta influencia. El objetivo principal de estos procedimientos es mecanizar ciertas tareas rutinarias. Este enfoque de selección automática se puede extender, y de hecho, hay varios “sistemas expertos” disponibles en el mercado. Por ejemplo, hay algoritmos disponibles que manejan “automáticamente” puntos inusuales como valores atípicos y puntos de alta influencia. Un modelo sugerido por los procedimientos automáticos de selección de variables debe estar sujeto a los mismos procedimientos cuidadosos de verificación diagnóstica que un modelo obtenido por cualquier otro medio.

5.3 Análisis de Residuales

Recuerde el papel de un residual en el modelo de regresión lineal introducido en la Sección 2.6. Un residual es una respuesta menos el valor ajustado correspondiente bajo el modelo. Dado que el modelo resume el efecto lineal de varias variables explicativas, podemos pensar en un residual como una respuesta controlada por los valores de las variables explicativas. Si el modelo es una representación adecuada de los datos, entonces los residuales deberían aproximarse a errores aleatorios. Los errores aleatorios se utilizan para representar la variación natural en el modelo; representan el resultado de un mecanismo impredecible. Por lo tanto, en la medida en que los residuales se parezcan a errores aleatorios, no debería haber patrones discernibles en los residuales. Los patrones en los residuales indican la presencia de información adicional que esperamos incorporar en el modelo. La ausencia de patrones en los residuales indica que el modelo parece explicar las relaciones principales en los datos.

5.3.1 Residuales

Hay al menos cuatro tipos de patrones que pueden descubrirse a través del análisis de residuales. En esta sección, discutimos los dos primeros: residuales que son inusuales y aquellos que están relacionados con otras variables explicativas. Luego introducimos el tercer tipo, residuales que muestran un patrón heterocedástico, en la Sección 5.7. En nuestro estudio de datos de series temporales que comienza en el Capítulo 7, introduciremos el cuarto tipo, residuales que muestran patrones a lo largo del tiempo.

Al examinar los residuales, generalmente es más fácil trabajar con un residual estandarizado, un residual que ha sido reescalado para no tener dimensiones. Generalmente trabajamos con residuales estandarizados porque así logramos transferir cierta experiencia de un conjunto de datos a otro y podemos enfocarnos en relaciones de interés. Al usar residuales estandarizados, podemos entrenarnos para observar una variedad de gráficos de residuales y reconocer inmediatamente un punto inusual al trabajar en unidades estándar.

Hay varias formas de definir un residual estandarizado. Usando $e_i = y_i - \hat{y}_i$ como el $i$-ésimo residual, aquí hay tres definiciones comúnmente usadas:

\[\begin{equation} \text{(a) }\frac{e_i}{s}, \quad \text{(b) }\frac{e_i}{s\sqrt{1 - h_{ii}}}, \quad \text{(c) }\frac{e_i}{s_{(i)}\sqrt{1 - h_{ii}}}. \tag{5.1} \end{equation}\]

Aquí, $h_{ii}$ es la influencia del $i$-ésimo punto. Se calcula en función de los valores de las variables explicativas y se definirá en la Sección 5.4.1. Recuerde que $s$ es la desviación estándar de los residuales (definida en la ecuación 3.8). De manera similar, definimos $s_{(i)}$ como la desviación estándar de los residuales al ejecutar una regresión después de eliminar la $i$-ésima observación.

Ahora, la primera definición en (a) es simple y fácil de explicar. Un cálculo simple muestra que la desviación estándar de la muestra de los residuales es aproximadamente $s$ (una razón por la que $s$ a menudo se denomina desviación estándar de los residuales). Por lo tanto, parece razonable estandarizar los residuales dividiendo por $s$.

La segunda opción presentada en (b), aunque más compleja, es más precisa. La varianza del $i$-ésimo residual es

\[ \text{Var}(e_i) = \sigma^2(1 - h_{ii}). \]

Este resultado se establecerá en la ecuación (5.15) de la Sección 5.10. Tenga en cuenta que esta varianza es menor que la varianza del término de error, Var$(\varepsilon_i) = \sigma^2$. Ahora, podemos reemplazar $\sigma$ por su estimación, $s$. Entonces, este resultado lleva a usar la cantidad $s\sqrt{1 - h_{ii}}$ como una desviación estándar estimada, o error estándar, para $e_i$. Por lo tanto, definimos el error estándar de $e_i$ como

\[ \text{se}(e_i) = s \sqrt{1 - h_{ii}}. \]

Siguiendo las convenciones introducidas en la Sección 2.6, en este texto usamos $e_i / \text{se}(e_i)$ como nuestro residual estandarizado.

La tercera opción presentada en (c) es una modificación de (b) y se conoce como un residual studentizado. Como se enfatiza en la Sección 5.3.2, un uso importante de los residuales es identificar respuestas inusualmente grandes. Ahora, supongamos que la $i$-ésima respuesta es inusualmente grande y que esto se mide a través de su residual. Este residual inusualmente grande también hará que el valor de $s$ sea grande. Debido a que el efecto grande aparece tanto en el numerador como en el denominador, el residual estandarizado puede no detectar esta respuesta inusual. Sin embargo, esta respuesta grande no inflará $s_{(i)}$ porque se construye después de eliminar la $i$-ésima observación. Por lo tanto, al usar residuales studentizados, obtenemos una mejor medida de las observaciones que tienen residuales inusualmente grandes. Al omitir esta observación de la estimación de $\sigma$, el tamaño de la observación solo afecta al numerador $e_i$ y no al denominador $s_{(i)}$.

Como otra ventaja, los residuales studentizados siguen una distribución $t$ con $n - (k + 1)$ grados de libertad, asumiendo que los errores están distribuidos normalmente (suposición E5). Este conocimiento de la distribución precisa nos ayuda a evaluar el grado de ajuste del modelo y es particularmente útil en muestras pequeñas. Es esta relación con la distribución $t$ de “Student” la que sugiere el nombre de “residuales studentizados”.

5.3.2 Uso de los Residuales para Identificar Valores Atípicos

Una función importante del análisis de residuales es identificar valores atípicos. Un valor atípico es una observación que no se ajusta bien al modelo; son observaciones donde el residual es inusualmente grande. Una regla general utilizada por muchos paquetes estadísticos es que una observación se marca como un valor atípico si el residual estandarizado excede dos en valor absoluto. En la medida en que la distribución de los residuales estandarizados imite la curva normal estándar, esperamos que solo una de cada 20 observaciones, o el 95%, exceda dos en valor absoluto y muy pocas observaciones excedan tres.

Los valores atípicos proporcionan una señal de que una observación debe investigarse para entender las causas especiales asociadas con este punto. Un valor atípico es una observación que parece inusual con respecto al resto del conjunto de datos. A menudo sucede que la razón de este comportamiento atípico puede descubrirse después de una investigación adicional. De hecho, este puede ser el propósito principal del análisis de regresión de un conjunto de datos.

Consideremos un ejemplo simple de lo que se llama análisis de desempeño. Supongamos que tenemos disponible una muestra de $n$ vendedores y estamos tratando de entender las ventas de cada persona en el segundo año en función de sus ventas en el primer año. Hasta cierto punto, esperamos que las ventas más altas en el primer año estén asociadas con ventas más altas en el segundo año. Las altas ventas pueden deberse a la habilidad natural del vendedor, ambición, buen territorio, etc. Las ventas del primer año pueden considerarse como una variable proxy que resume estos factores. Esperamos variación en el desempeño de ventas tanto de manera transversal como a lo largo de los años. Es interesante cuando un vendedor tiene un desempeño inusualmente bueno (o malo) en el segundo año en comparación con su desempeño en el primer año. Los residuales proporcionan un mecanismo formal para evaluar las ventas del segundo año después de controlar los efectos de las ventas del primer año.

Hay varias opciones disponibles para manejar valores atípicos.

Opciones para Manejar Valores Atípicos

Incluir la observación en las estadísticas resumen habituales pero comentar sobre sus efectos. Un valor atípico puede ser grande pero no tan grande como para sesgar los resultados de todo el análisis. Si no se pueden determinar causas especiales para esta observación inusual, entonces esta observación puede simplemente reflejar la variabilidad en los datos.
Eliminar la observación del conjunto de datos. Puede determinarse que la observación no es representativa de la población de la cual se extrae la muestra. Si este es el caso, entonces puede haber poca información contenida en la observación que pueda usarse para hacer afirmaciones generales sobre la población. Esta opción implica que omitiríamos la observación de las estadísticas resumen de la regresión y la discutiríamos en nuestro informe como un caso separado.
Crear una variable binaria para indicar la presencia de un valor atípico. Si se han identificado una o varias causas especiales para explicar un valor atípico, entonces estas causas podrían introducirse formalmente en el procedimiento de modelado mediante la introducción de una variable que indique la presencia (o ausencia) de estas causas. Este enfoque es similar a la eliminación de puntos, pero permite que el valor atípico se incluya formalmente en la formulación del modelo, de modo que, si surgen observaciones adicionales afectadas por las mismas causas, se puedan manejar de forma automática.

5.3.3 Uso de los Residuales para Seleccionar Variables Explicativas

Otra función importante del análisis de residuales es ayudar a identificar variables explicativas adicionales que puedan usarse para mejorar la formulación del modelo. Si hemos especificado el modelo correctamente, entonces los residuales deberían parecerse a errores aleatorios y no contener patrones discernibles. Por lo tanto, al comparar residuales con variables explicativas, no esperamos ninguna relación. Si detectamos una relación, esto sugiere la necesidad de controlar esta variable adicional. Esto se puede lograr introduciendo la variable adicional en el modelo de regresión.

Las relaciones entre los residuales y las variables explicativas pueden establecerse rápidamente utilizando estadísticas de correlación. Sin embargo, si una variable explicativa ya está incluida en el modelo de regresión, entonces la correlación entre los residuales y una variable explicativa será cero (ver Sección 5.10.1 para la demostración algebraica). Es una buena idea reforzar esta correlación con un diagrama de dispersión. Un gráfico de residuales frente a variables explicativas no solo reforzará gráficamente la estadística de correlación, sino que también servirá para detectar posibles relaciones no lineales. Por ejemplo, una relación cuadrática puede detectarse utilizando un diagrama de dispersión, no una estadística de correlación.

Si detecta una relación entre los residuales de un ajuste de modelo preliminar y una variable explicativa adicional, introducir esta variable adicional no siempre mejorará la especificación de su modelo. La razón es que la variable adicional puede estar relacionada linealmente con las variables que ya están en el modelo. Si desea una garantía de que agregar una variable adicional mejorará su modelo, entonces construya un gráfico de variables añadidas (ver Sección 3.4.3).

En resumen, después de un ajuste preliminar del modelo, debe:

Calcular estadísticas resumen y mostrar la distribución de los residuales (estandarizados) para identificar valores atípicos.
Calcular la correlación entre los residuales (estandarizados) y las variables explicativas adicionales para buscar relaciones lineales.
Crear gráficos de dispersión entre los residuales (estandarizados) y las variables explicativas adicionales para buscar relaciones no lineales.

Ejemplo: Liquidez del Mercado de Valores. La decisión de un inversor de comprar una acción generalmente se toma teniendo en cuenta varios criterios. Primero, los inversores suelen buscar un alto rendimiento esperado. Un segundo criterio es el riesgo de una acción, que puede medirse mediante la variabilidad de los rendimientos. Tercero, muchos inversores están preocupados por el tiempo que están comprometiendo su capital con la compra de un valor. Muchas acciones de ingresos, como las de servicios públicos, devuelven regularmente partes de las inversiones de capital en forma de dividendos. Otras acciones, particularmente las de crecimiento, no devuelven nada hasta la venta del valor. Por lo tanto, la duración promedio de la inversión en un valor es otro criterio. Cuarto, a los inversores les preocupa la capacidad de vender la acción en cualquier momento que sea conveniente para ellos. Nos referimos a este cuarto criterio como la liquidez de la acción. Cuanto más líquida sea la acción, más fácil será venderla. Para medir la liquidez, en este estudio utilizamos el número de acciones negociadas en una bolsa durante un período de tiempo específico (llamado VOLUME). Estamos interesados en estudiar la relación entre el volumen y otras características financieras de una acción.

Comenzamos este estudio con 126 empresas cuyas opciones se negociaron el 3 de diciembre de 1984. Los datos de las acciones fueron obtenidos de Francis Emory Fitch, Inc. para el período del 3 de diciembre de 1984 al 28 de febrero de 1985. Para las variables de actividad comercial, examinamos:

El volumen total de negociación de tres meses (VOLUME, en millones de acciones),
El número total de transacciones de tres meses (NTRAN), y
El tiempo promedio entre transacciones (AVGT, medido en minutos).

Para las variables de tamaño de la empresa, utilizamos:

El precio de apertura de la acción el 2 de enero de 1985 (PRICE),
El número de acciones en circulación el 31 de diciembre de 1984 (SHARE, en millones de acciones), y
El valor de mercado del capital (VALUE, en miles de millones de dólares) obtenido al tomar el producto de PRICE y SHARE.

Finalmente, para el apalancamiento financiero, examinamos la relación deuda-capital (DEB_EQ) obtenida de la Cinta Industrial de Compustat y el manual de Moody’s. Los datos en SHARE se obtienen de la cinta mensual del Centro de Investigación en Precios de Seguridad (CRSP).

Después de examinar algunas estadísticas resumen preliminares de los datos, se eliminaron tres empresas porque tenían un volumen inusualmente alto o un precio elevado. Estas son Teledyne y Capital Cities Communication, cuyos precios eran más de cuatro veces el precio promedio de las demás empresas, y American Telephone and Telegraph, cuyo volumen total era más de siete veces el volumen total promedio de las demás empresas. Basado en una investigación adicional, cuyos detalles no se presentan aquí, estas empresas fueron eliminadas porque parecían representar circunstancias especiales que no deseábamos modelar.

La Tabla 5.2 resume las estadísticas descriptivas basadas en las $n = 123$ empresas restantes. Por ejemplo, en la Tabla 5.2, vemos que el tiempo promedio entre transacciones es de aproximadamente cinco minutos y este tiempo varía desde un mínimo de menos de 1 minuto hasta un máximo de aproximadamente 20 minutos.

Tabla 5.2: **Estadísticas Resumen de las Variables de Liquidez de las Acciones**
	Media	Mediana	Desviación Estándar	Mínimo	Máximo
VOLUME	13.423	11.556	10.632	0.658	64.572
AVGT	5.441	4.284	3.853	0.590	20.772
NTRAN	6436.000	5071.000	5310.000	999.000	36420.000
PRICE	38.800	34.380	21.370	9.120	122.380
SHARE	94.730	53.830	115.100	6.740	783.050
VALUE	4.116	2.065	8.157	0.115	75.437
DEBEQ	2.697	1.105	6.509	0.185	53.628

Fuente: Francis Emory Fitch, Inc., Standard & Poor’s Compustat, y el Centro de Investigación de Precios de Valores de la Universidad de Chicago.

La Tabla 5.3 reporta los coeficientes de correlación y la Figura 5.2 proporciona la matriz de dispersión correspondiente. Si tienes conocimientos en finanzas, te resultará interesante notar que el apalancamiento financiero, medido por DEB_EQ, no parece estar relacionado con las otras variables. A partir del diagrama de dispersión y la matriz de correlación, vemos una fuerte relación entre VOLUME y el tamaño de la empresa, medido por SHARE y VALUE. Además, las tres variables de actividad de negociación, VOLUME, AVGT y NTRAN, están altamente relacionadas entre sí.

Tabla 5.3: **Matriz de Correlación de la Liquidez de las Acciones**
	AVGT	NTRAN	PRICE	SHARE	VALUE	DEB_EQ	VOLUME
AVGT	1.000	-0.668	-0.128	-0.429	-0.318	0.094	-0.674
NTRAN	-0.668	1.000	0.190	0.817	0.760	-0.092	0.913
PRICE	-0.128	0.190	1.000	0.177	0.457	-0.038	0.168
SHARE	-0.429	0.817	0.177	1.000	0.829	-0.077	0.773
VALUE	-0.318	0.760	0.457	0.829	1.000	-0.077	0.702
DEB_EQ	0.094	-0.092	-0.038	-0.077	-0.077	1.000	-0.052
VOLUME	-0.674	0.913	0.168	0.773	0.702	-0.052	1.000

Código R para Producir las Tablas 5.2 y 5.3

La Figura 5.2 muestra que la variable AVGT está inversamente relacionada con VOLUME y NTRAN está inversamente relacionada con AVGT. De hecho, resultó que la correlación entre el tiempo promedio entre transacciones y el recíproco del número de transacciones fue del $99.98\%!$ Esto no es tan sorprendente cuando se piensa en cómo se podría calcular AVGT. Por ejemplo, en la Bolsa de Valores de Nueva York, el mercado está abierto de 10:00 A.M. a 4:00 P.M. Para cada acción en un día particular, el tiempo promedio entre transacciones multiplicado por el número de transacciones es casi igual a 360 minutos (= 6 horas). Por lo tanto, excepto por errores de redondeo porque las transacciones solo se registran al minuto más cercano, hay una relación lineal perfecta entre AVGT y el recíproco de NTRAN.

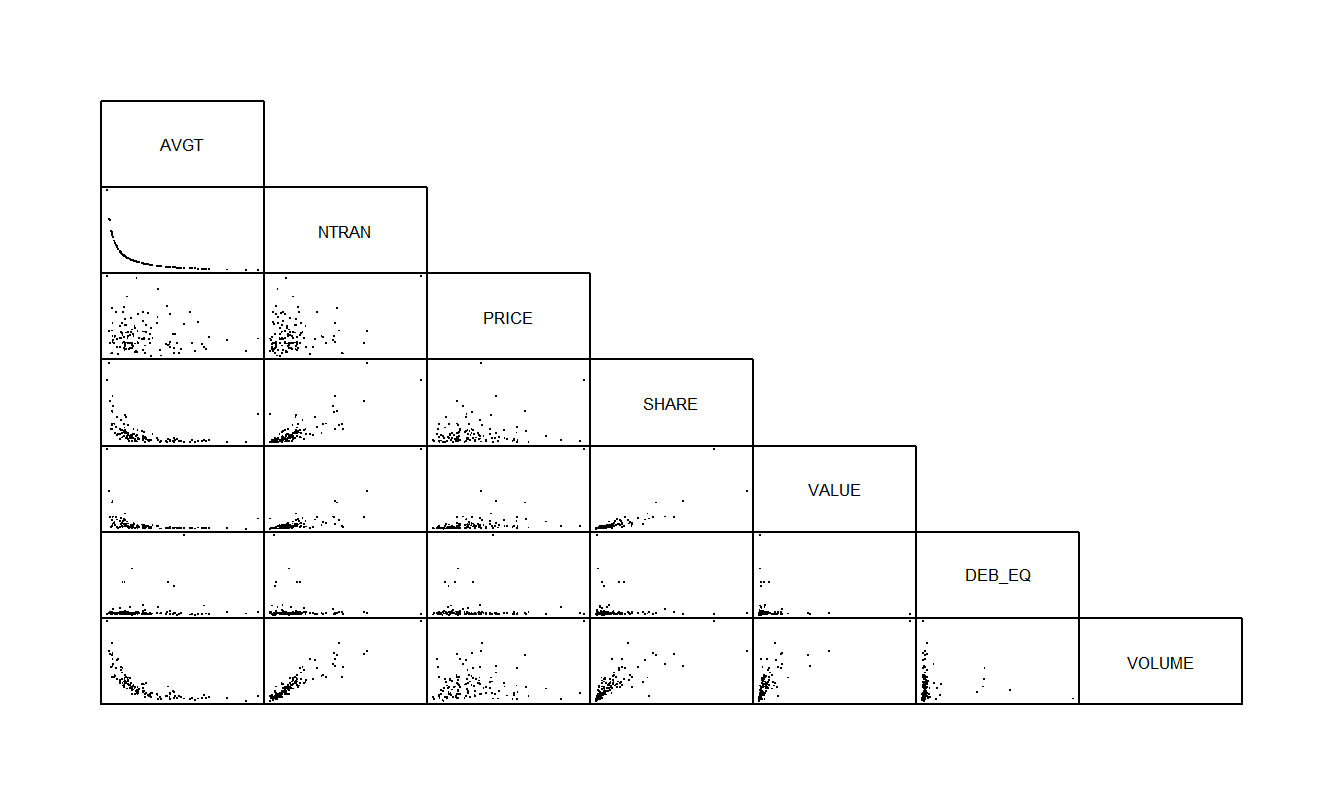
Matriz de dispersión para las variables de liquidez de las acciones. La variable del número de transacciones (NTRAN) parece estar fuertemente relacionada con el VOLUME de acciones negociadas e inversamente relacionada con AVGT.

Figura 5.2: Matriz de dispersión para las variables de liquidez de las acciones. La variable del número de transacciones (NTRAN) parece estar fuertemente relacionada con el VOLUME de acciones negociadas e inversamente relacionada con AVGT.

Para comenzar a entender la medida de liquidez VOLUME, primero ajustamos un modelo de regresión utilizando NTRAN como una variable explicativa. El modelo de regresión ajustado es:

\[ \small{ \begin{array}{lcc} \text{VOLUME} &= 1.65 &+ 0.00183 \text{ NTRAN} \\ \text{errores estándar} & (0.6173) & (0.000074) \end{array} } \]

con $R^2 = 83.4\%$ y $s = 4.35$. Note que el cociente $t$ para la pendiente asociada con NTRAN es

\[ t(b_1) = \frac{b_1}{se(b_1)} = \frac{0.00183}{0.000074} = 24.7 \]

indicando una fuerte significancia estadística. Los residuos se calcularon utilizando este modelo estimado. Para ver si los residuos están relacionados con otras variables explicativas, la Tabla 5.4 muestra las correlaciones.

Tabla 5.4: **Primera Tabla de Correlaciones**
Variable	AVGT	PRICE	SHARE	VALUE	DEB_EQ
RESID	-0.159	-0.014	0.064	0.018	0.078

Nota: Los residuos se crearon a partir de una regresión de VOLUME sobre NTRAN.

La correlación entre el residuo y AVGT y el diagrama de dispersión (no mostrado aquí) indica que puede haber alguna información en la variable AVGT en el residuo. Por lo tanto, parece razonable usar AVGT directamente en el modelo de regresión. Recuerde que estamos interpretando el residuo como el valor de VOLUME habiendo controlado el efecto de NTRAN.

A continuación, ajustamos un modelo de regresión utilizando NTRAN y AVGT como variables explicativas. El modelo de regresión ajustado es:

\[ \small{ \begin{array}{lccc} \text{VOLUME} &= 4.41 &- 0.322 \text{ AVGT} &+ 0.00167 \text{ NTRAN} \\ \text{errores estándar} & (1.30)& (0.135)& (0.000098) \end{array} } \]

con $R^2 = 84.2\%$ y $s = 4.26$. Basado en el cociente $t$ para AVGT, $t(b_{AVGT}) = \frac{-0.322}{0.135} = -2.39$, parece que AVGT es una variable explicativa útil en el modelo. Note también que $s$ ha disminuido, lo que indica que $R_a^2$ ha aumentado.

La Tabla 5.5 proporciona correlaciones entre los residuos del modelo y otras posibles variables explicativas e indica que no parece haber mucha información adicional en las variables explicativas. Esto se reafirma por la tabla correspondiente de diagramas de dispersión en la Figura 5.3. Los histogramas en la Figura 5.3 sugieren que, aunque la distribución de los residuos es bastante simétrica, la distribución de cada variable explicativa está sesgada. Debido a esto, se exploraron transformaciones de las variables explicativas. Esta línea de pensamiento no proporcionó mejoras reales y, por lo tanto, no se proporcionan detalles aquí.

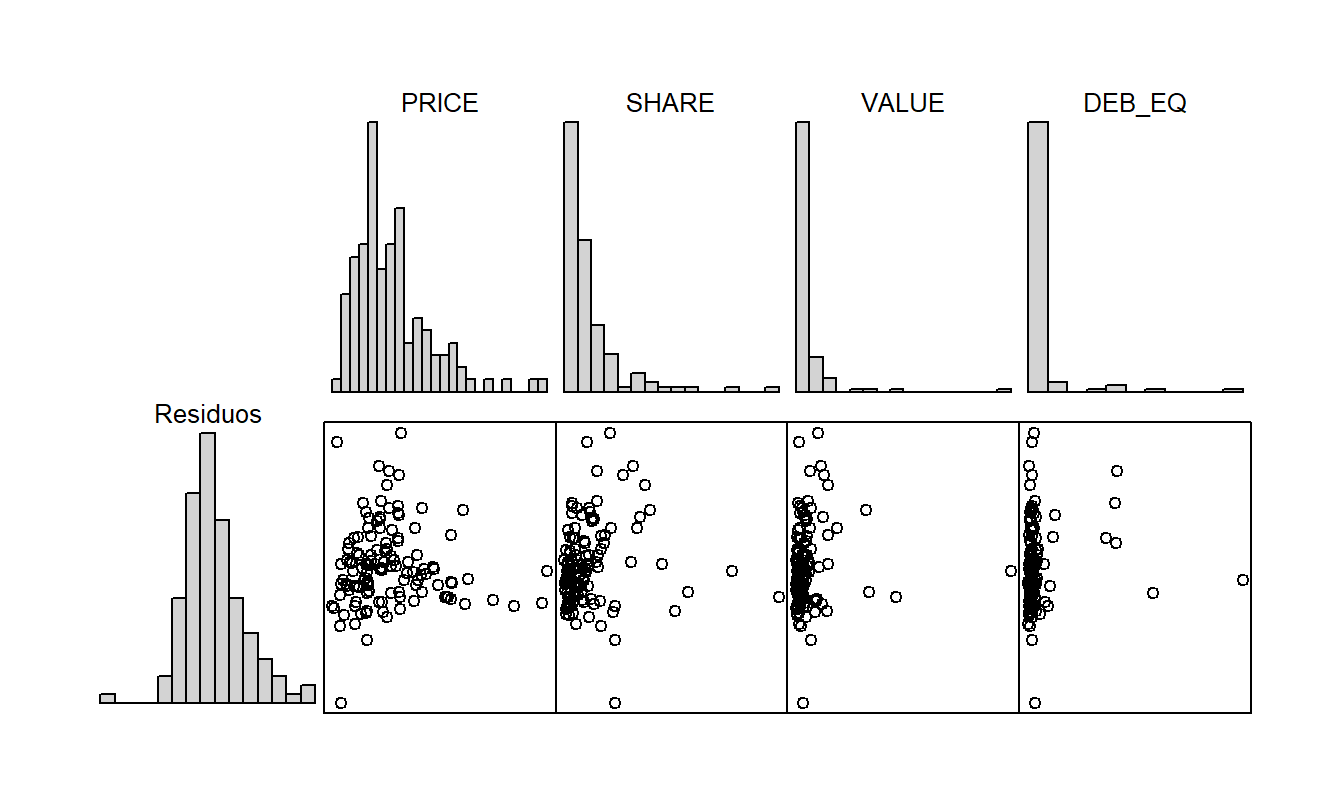
Matriz de dispersión de los residuos de la regresión de VOLUME sobre NTRAN y AVGT en el eje vertical y las variables predictoras restantes en los ejes horizontales.

Figura 5.3: Matriz de dispersión de los residuos de la regresión de VOLUME sobre NTRAN y AVGT en el eje vertical y las variables predictoras restantes en los ejes horizontales.

Tabla 5.5: **Segunda Tabla de Correlaciones**
Variable	PRICE	SHARE	VALUE	DEB_EQ
RESID	-0.015	0.100	0.074	0.089

Nota: Los residuos se crearon a partir de una regresión de VOLUME sobre NTRAN y AVGT.

5.4 Puntos Influyentes

No todos los puntos son creados iguales; en esta sección veremos que ciertas observaciones pueden tener un efecto desproporcionado en el ajuste general de la regresión. A estos puntos los llamaremos “influyentes.” Esto no es tan sorprendente; ya hemos visto que las estimaciones de los coeficientes de regresión son sumas ponderadas de respuestas (ver Sección 3.2.4). Algunas observaciones tienen pesos mayores que otras y, por lo tanto, tienen una mayor influencia en las estimaciones de los coeficientes de regresión. Por supuesto, el hecho de que una observación sea influyente no significa que sea incorrecta o que su impacto en el modelo sea engañoso. Como analistas, simplemente nos gustaría saber si nuestro modelo ajustado es sensible a cambios leves, como la eliminación de un solo punto, para sentirnos cómodos al generalizar nuestros resultados de la muestra a una población más grande.

Para evaluar la influencia, pensamos en observaciones como respuestas inusuales, dadas un conjunto de variables explicativas, o que tienen un conjunto inusual de valores de variables explicativas. Ya hemos visto en la Sección 5.3 cómo evaluar respuestas inusuales utilizando residuos. Esta sección se centra en conjuntos inusuales de valores de variables explicativas.

5.4.1 Apalancamiento

Introdujimos este tema en la Sección 2.6, donde llamamos a una observación con una variable explicativa inusual un “punto de alto apalancamiento.” Con más de una variable explicativa, determinar si una observación es un punto de alto apalancamiento no es tan sencillo. Por ejemplo, es posible que una observación “no sea inusual” para ninguna variable individual y, sin embargo, sea inusual en el espacio de variables explicativas. Considere el conjunto de datos ficticio representado en la Figura 5.4. Visualmente, parece claro que el punto marcado en la esquina superior derecha es inusual. Sin embargo, no es inusual cuando se examina el histograma de $x_1$ o de $x_2$. Es inusual solo cuando se consideran las variables explicativas de manera conjunta.

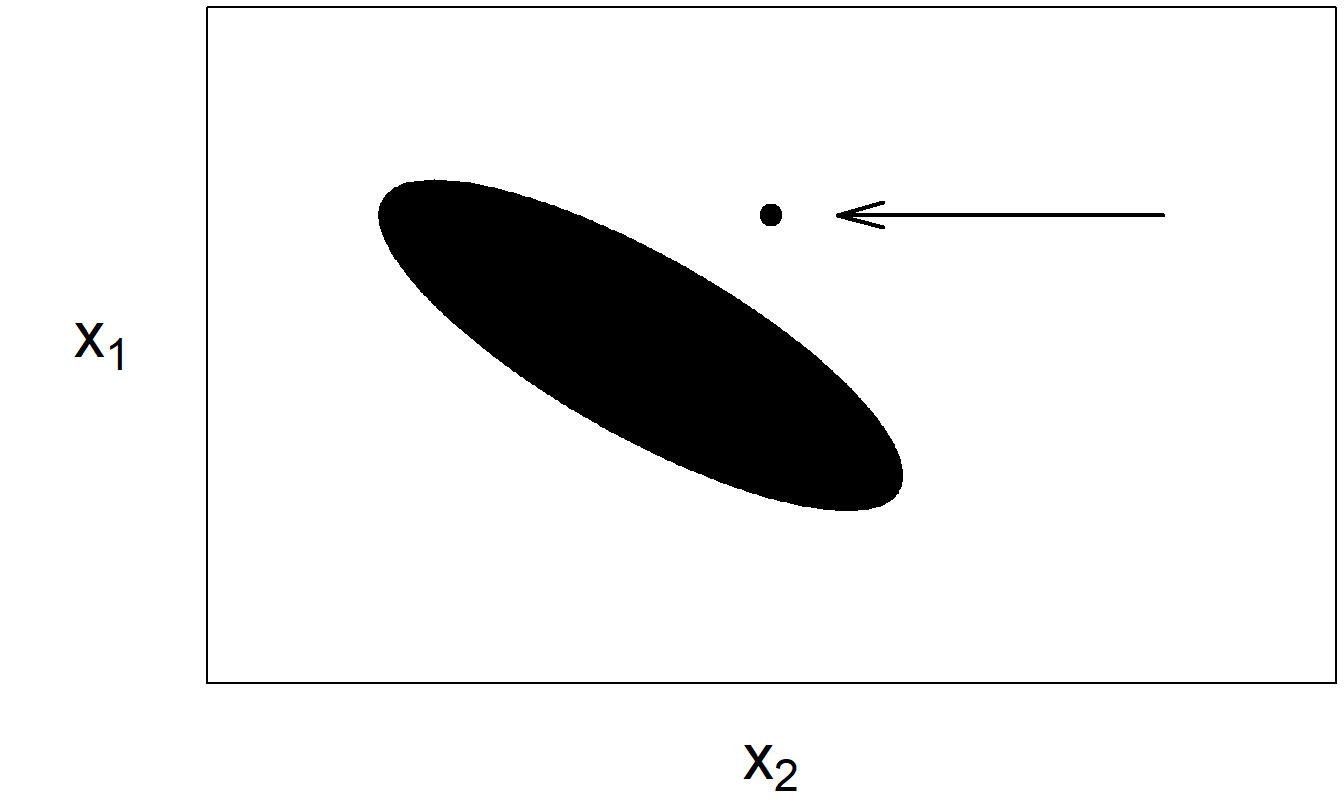
Figura 5.4: El elipsoide representa la mayoría de los datos. La flecha marca un punto inusual.

Para dos variables explicativas, esto es evidente al examinar los datos gráficamente. Debido a que es difícil examinar gráficamente los datos con más de dos variables explicativas, necesitamos un procedimiento numérico para evaluar el apalancamiento.

Para definir el concepto de apalancamiento en la regresión lineal múltiple, utilizamos algunos conceptos de álgebra matricial. Específicamente, en la Sección 3.1 mostramos que el vector de coeficientes de regresión de mínimos cuadrados se puede calcular usando $\mathbf{b} = (\mathbf{X}^{\prime} \mathbf{X})^{-1} \mathbf{X}^{\prime} \mathbf{y}$. Así, podemos expresar el vector de valores ajustados $\hat{\mathbf{y}} = (\hat{y}_1, \ldots, \hat{y}_n)^{\prime}$ como

\[\begin{equation} \mathbf{\hat{y}} = \mathbf{Xb} . \tag{5.2} \end{equation}\]

De manera similar, el vector de residuos es el vector de respuesta menos el vector de valores ajustados, es decir, $\mathbf{e} = \mathbf{y - \hat{y}}$.

A partir de la expresión para los coeficientes de regresión $\mathbf{b}$ en la ecuación (3.4), tenemos

\[ \mathbf{\hat{y}} = \mathbf{X} (\mathbf{X}^{\prime} \mathbf{X})^{-1} \mathbf{X}^{\prime} \mathbf{y} \]

Esta ecuación sugiere definir

\[ \mathbf{H} = \mathbf{X} (\mathbf{X}^{\prime} \mathbf{X})^{-1} \mathbf{X}^{\prime} \]

de modo que

\[ \mathbf{\hat{y}} = \mathbf{Hy} \]

A partir de esto, se dice que la matriz $\mathbf{H}$ proyecta el vector de respuestas $\mathbf{y}$ en el vector de valores ajustados $\mathbf{\hat{y}}$. Alternativamente, puede pensar en $\mathbf{H}$ como la matriz que pone el “sombrero,” o circunflejo, en $\mathbf{y}$. A partir de la $i$-ésima fila de la ecuación vectorial $\mathbf{\hat{y}} = \mathbf{Hy}$, tenemos

\[ \hat{y}_i = h_{i1} y_1 + h_{i2} y_2 + \cdots + h_{ii} y_i + \cdots + h_{in} y_n \]

Aquí, $h_{ij}$ es el número en la $i$-ésima fila y $j$-ésima columna de $\mathbf{H}$. A partir de esta expresión, vemos que cuanto mayor sea $h_{ii}$, mayor será el efecto que la $i$-ésima respuesta $(y_i)$ tiene en el valor ajustado correspondiente $(\hat{y}_i)$. Por lo tanto, llamamos a $h_{ii}$ el apalancamiento para la $i$-ésima observación. Debido a que $h_{ii}$ es el elemento diagonal $i$-ésimo de $\mathbf{H}$, una expresión directa para $h_{ii}$ es

\[\begin{equation} h_{ii} = \mathbf{x}_i^{\prime} (\mathbf{X}^{\prime} \mathbf{X})^{-1} \mathbf{x}_i \tag{5.3} \end{equation}\]

donde $\mathbf{x}_i = (x_{i0}, x_{i1}, \ldots, x_{ik})^{\prime}$. Debido a que los valores de $h_{ii}$ se calculan en base a las variables explicativas, los valores de la variable de respuesta no afectan el cálculo de los apalancamientos.

Los valores altos de apalancamiento indican que una observación puede tener un efecto desproporcionado en el ajuste, esencialmente porque está distante de las otras observaciones (al observar el espacio de variables explicativas). ¿Qué tan grande es grande? Existen algunas pautas de álgebra matricial, donde tenemos que

\[ \frac{1}{n} \leq h_{ii} \leq 1 \]

\[ \bar{h} = \frac{1}{n} \sum_{i=1}^{n} h_{ii} = \frac{k+1}{n}. \]

Por lo tanto, cada apalancamiento está limitado por $n^{-1}$ y $1$, y el apalancamiento promedio es igual al número de coeficientes de regresión dividido por el número de observaciones. A partir de estos y argumentos relacionados, utilizamos una convención ampliamente adoptada y declaramos que una observación es un punto de alto apalancamiento si el apalancamiento supera tres veces el promedio, es decir, si

\[ h_{ii} > \frac{3(k+1)}{n}. \]

Una vez identificados los puntos de alto apalancamiento, al igual que con los valores atípicos, es importante que el analista busque causas especiales que puedan haber producido estos puntos inusuales. Para ilustrar, en la Sección 2.7 identificamos el colapso del mercado de 1987 como la razón detrás del punto de alto apalancamiento. Además, los puntos de alto apalancamiento a menudo se deben a errores administrativos al codificar los datos, que pueden o no ser fáciles de rectificar. En general, las opciones para manejar puntos de alto apalancamiento son similares a las disponibles para tratar con valores atípicos.

Opciones para Manejar Puntos de Alto Apalancamiento

Incluir la observación en las estadísticas resumidas pero comentar sobre su efecto. Por ejemplo, una observación puede apenas superar un límite y su efecto puede no ser importante en el análisis general.
Eliminar la observación del conjunto de datos. Nuevamente, la justificación básica para esta acción es que se considera que la observación no es representativa de una población más grande. Una opción intermedia entre (1) y (2) es presentar el análisis tanto con como sin el punto de alto apalancamiento. De esta manera, se demuestra completamente el impacto del punto y el lector de su análisis puede decidir cuál opción es más adecuada.
Elegir otra variable para representar la información. En algunos casos, otra variable explicativa estará disponible para servir como reemplazo. Por ejemplo, en un ejemplo de alquileres de apartamentos, podríamos usar el número de habitaciones para reemplazar una variable de metros cuadrados como medida del tamaño del apartamento. Aunque los metros cuadrados de un apartamento pueden ser inusualmente grandes, lo que lo convierte en un punto de alto apalancamiento, puede tener una, dos o tres habitaciones, dependiendo de la muestra examinada.
Usar una transformación no lineal de una variable explicativa. Para ilustrar, con nuestro ejemplo de Liquidez de Acciones en la Sección 5.5.3, podemos transformar la variable continua de razón deuda a capital DEB_EQ en una variable que indique la presencia de “alta” razón deuda a capital. Por ejemplo, podríamos codificar DE_IND = 1 si DEB_EQ > 5 y DE_IND = 0 si DEB_EQ ≤ 5. Con esta recodificación, aún conservamos información sobre el apalancamiento financiero de una empresa sin permitir que los valores grandes de DEB_EQ influyan en el ajuste de la regresión.

Algunos analistas usan metodologías de estimación “robustas” como alternativa a la estimación de mínimos cuadrados. La idea básica de estas técnicas es reducir el efecto de cualquier observación en particular. Estas técnicas son útiles para reducir el efecto tanto de valores atípicos como de puntos de alto apalancamiento. Esta táctica puede considerarse intermedia entre un procedimiento extremo, ignorando el efecto de puntos inusuales, y otro extremo, dando plena credibilidad a los puntos inusuales al eliminarlos del conjunto de datos. La palabra robusto sugiere que estas metodologías de estimación son “saludables” incluso cuando son atacadas por una observación ocasionalmente mala (un germen). Hemos visto que esto no es cierto para la estimación de mínimos cuadrados.

5.4.2 Distancia de Cook

Para cuantificar la influencia de un punto, una medida que considera tanto las variables de respuesta como las explicativas es la Distancia de Cook. Esta distancia, $D_i$, se define como

\[\begin{equation} \begin{array}{ll} D_i &= \frac{\sum_{j=1}^{n} (\hat{y}_j - \hat{y}_{j(i)})^2}{(k+1) s^2} \tag{5.4} \\ &= \left( \frac{e_i}{se(e_i)} \right)^2 \frac{h_{ii}}{(k+1)(1 - h_{ii})}. \end{array} \end{equation}\]

La primera expresión proporciona una definición. Aquí, $\hat{y}_{j(i)}$ es la predicción de la $j$-ésima observación, calculada excluyendo la $i$-ésima observación del ajuste de regresión. Para medir el impacto de la $i$-ésima observación, comparamos los valores ajustados con y sin la $i$-ésima observación. Cada diferencia se eleva al cuadrado y se suma en todas las observaciones para resumir el impacto.

La segunda ecuación proporciona otra interpretación de la distancia $D_i$. La primera parte, $\left( \frac{e_i}{se(e_i)} \right)^2$, es el cuadrado del residuo estandarizado $i$-ésimo. La segunda parte, $\frac{h_{ii}}{(k+1)(1 - h_{ii})}$, se atribuye únicamente al apalancamiento. Así, la distancia $D_i$ se compone de una medida para valores atípicos multiplicada por una medida de apalancamiento. De esta manera, la distancia de Cook tiene en cuenta tanto las variables de respuesta como las explicativas. La Sección 5.10.3 establece la validez de la ecuación (5.4).

Para tener una idea del tamaño esperado de $D_i$ para un punto que no es inusual, recuerde que esperamos que los residuos estandarizados sean aproximadamente uno y que el apalancamiento $h_{ii}$ sea aproximadamente $\frac{k+1}{n}$. Por lo tanto, anticipamos que $D_i$ debería ser aproximadamente $\frac{1}{n}$. Otra regla general es comparar $D_i$ con una distribución $F$ con $df_1 = k+1$ y $df_2 = n - (k+1)$ grados de libertad. Los valores de $D_i$ que son grandes en comparación con esta distribución merecen atención.

Ejemplo: Valores Atípicos y Puntos de Alto Apalancamiento - Continuación. Para ilustrar, volvemos a nuestro ejemplo de la Sección 2.6. En este ejemplo, consideramos 19 puntos “buenos” o base, más cada uno de los tres tipos de puntos inusuales, etiquetados como A, B y C. La Tabla 5.6 resume los cálculos.

Tabla 5.6: **Medidas de Tres Tipos de Puntos Inusuales**
Observation	Standardized Residual $e / se(e)$	Leverage $h$	Cook’s Distance $D$
A	4.00	0.067	0.577
B	0.77	0.550	0.363
C	-4.01	0.550	9.832

Como se mencionó en la Sección 2.6, de la columna de residuos estandarizados vemos que tanto los puntos A como C son valores atípicos. Para juzgar el tamaño de los apalancamientos, dado que hay $n=20$ puntos, los apalancamientos están limitados por 0.05 y 1.00, con el apalancamiento promedio siendo $\bar{h} = \frac{2}{20} = 0.10$. Usando 0.3 ($= 3 \times \bar{h}$) como un umbral, tanto los puntos B como C son puntos de alto apalancamiento. Nótese que sus valores son los mismos. Esto se debe a que, según la Figura 2.7, los valores de las variables explicativas son los mismos y solo la variable de respuesta ha cambiado. La columna de la distancia de Cook captura ambos tipos de comportamiento inusual. Dado que el valor típico de $D_i$ es $\frac{1}{n}$ o 0.05, la distancia de Cook proporciona una estadística para alertarnos de que cada punto es inusual en un aspecto u otro. En particular, el punto C tiene un $D_i$ muy grande, lo que refleja el hecho de que es tanto un valor atípico como un punto de alto apalancamiento. El percentil 95 de una distribución $F$ con $df_1 = 2$ y $df_2 = 18$ es 3.555. El hecho de que el punto C tenga un valor de $D_i$ que supera con creces este umbral indica la influencia sustancial de este punto.

5.5 Colinealidad

5.5.1 ¿Qué es la Colinealidad?

Colinealidad, o multicolinealidad, ocurre cuando una variable explicativa es, o casi es, una combinación lineal de las otras variables explicativas. Intuitivamente, con datos colineales, es útil pensar en las variables explicativas como altamente correlacionadas entre sí. Si una variable explicativa es colineal, surge la pregunta de si es redundante, es decir, si la variable proporciona poca información adicional sobre la información que ya está en las otras variables explicativas. Las preguntas son: ¿Es importante la colinealidad? Si es así, ¿cómo afecta el ajuste de nuestro modelo y cómo la detectamos? Para abordar la primera pregunta, considere un ejemplo algo patológico.

Ejemplo: Variables Explicativas Perfectamente Correlacionadas. Joe Finance fue solicitado para ajustar el modelo $\mathrm{E} ~y = \beta_0 + \beta_1 x_1 + \beta_2 x_2$ a un conjunto de datos. Su modelo ajustado resultante fue $\hat{y} = -87 + x_1 + 18 x_2.$ El conjunto de datos considerado es:

\[ \begin{array}{l|cccc} \hline i & 1 & 2 & 3 & 4 \\ \hline y_i & 23 & 83 & 63 & 103 \\ x_{i1} & 2 & 8 &6 & 10 \\ x_{i2} & 6 & 9 & 8 & 10 \\ \hline \end{array} \]

Joe verificó el ajuste para cada observación. Joe estaba muy contento porque ajustó los datos perfectamente. Por ejemplo, para la tercera observación, el valor ajustado es $\hat{y}_3 = -87 + 6 + 18 \times 8 = 63$, que es igual a la tercera respuesta, $y_3$. Debido a que la respuesta es igual al valor ajustado, el residuo es cero. Puede verificar que esto es cierto para cada observación, y así, el $R^2$ resultó ser $100\%$.

Sin embargo, Jane Actuary llegó y ajustó el modelo $\hat{y} = -7 + 9 x_1 + 2 x_2.$ Jane realizó las mismas comprobaciones cuidadosas que Joe hizo y también obtuvo un ajuste perfecto ($R^2 = 1$). ¿Quién tiene razón?

La respuesta es ambos y ninguno. De hecho, hay un número infinito de ajustes. Esto se debe a la relación perfecta $x_2 = 5 + \frac{x_1}{2}$ entre las dos variables explicativas.

Este ejemplo ilustra algunos hechos importantes sobre la colinealidad.

Hechos sobre la Colinealidad

La colinealidad no nos impide obtener buenos ajustes ni hacer predicciones de nuevas observaciones. Nótese que en el ejemplo anterior obtuvimos ajustes perfectos.
Las estimaciones de las varianzas de error y, por lo tanto, las pruebas de adecuación del modelo, siguen siendo fiables.
En casos de colinealidad severa, los errores estándar de los coeficientes de regresión individuales son mayores que en los casos en que, ceteris paribus, no existe colinealidad severa. Con errores estándar grandes, los coeficientes de regresión individuales pueden no ser significativos. Además, debido a que un error estándar grande significa que el correspondiente cociente $t$ es pequeño, es difícil detectar la importancia de una variable.

Para detectar la colinealidad, comience con una matriz de coeficientes de correlación de las variables explicativas. Esta matriz es fácil de crear, fácil de interpretar y captura rápidamente las relaciones lineales entre pares de variables. Una matriz de diagramas de dispersión proporciona un refuerzo visual de las estadísticas resumidas en la matriz de correlación.

5.5.2 Factores de Inflación de Varianza

Las matrices de correlación y diagramas de dispersión capturan solo las relaciones entre pares de variables. Para capturar relaciones más complejas entre varias variables, introducimos el factor de inflación de varianza (VIF). Para definir un VIF, suponga que el conjunto de variables explicativas está etiquetado como $x_1, x_2, \ldots, x_{k}$. Ahora, ejecute la regresión utilizando $x_j$ como la “respuesta” y los otros $x$ ($x_1, x_2, \ldots, x_{j-1}, x_{j+1}, \ldots, x_{k}$) como las variables explicativas. Denote el coeficiente de determinación de esta regresión por $R_j^2$. Interpretamos $R_j = \sqrt{R_j^2}$ como el coeficiente de correlación múltiple entre $x_j$ y las combinaciones lineales de los otros $x$. A partir de este coeficiente de determinación, definimos el factor de inflación de varianza

\[ VIF_j = \frac{1}{1 - R_j^2}, \text{ para } j = 1, 2, \ldots, k. \]

Un mayor $R_j^2$ resulta en un mayor $VIF_j$; esto significa una mayor colinealidad entre $x_j$ y los otros $x$. Ahora, $R_j^2$ por sí solo es suficiente para capturar la relación lineal de interés. Sin embargo, usamos $VIF_j$ en lugar de $R_j^2$ como nuestra medida de colinealidad debido a la relación algebraica

\[\begin{equation} se(b_j) = s \frac{\sqrt{VIF_j}}{s_{x_j} \sqrt{n - 1}}. \tag{5.5} \end{equation}\]

Aquí, $se(b_j)$ y $s$ son errores estándar y la desviación estándar residual de un ajuste completo de regresión de $y$ sobre $x_1, \ldots, x_{k}$. Además, $s_{x_j} = \sqrt{(n - 1)^{-1} \sum_{i=1}^{n} (x_{ij} - \bar{x}_j)^2 }$ es la desviación estándar muestral de la $j$-ésima variable $x_j$. La Sección 5.10.3 proporciona una verificación de la ecuación (5.5).

Así, un mayor $VIF_j$ resulta en un mayor error estándar asociado con la pendiente $j$-ésima, $b_j$. Recuerde que $se(b_j)$ es $s$ veces la raíz cuadrada del $(j+1)$-ésimo elemento diagonal de $(\mathbf{X}^{\prime} \mathbf{X})^{-1}$. La idea es que cuando ocurre colinealidad, la matriz $\mathbf{X}^{\prime} \mathbf{X}$ tiene propiedades similares al número cero. Cuando intentamos calcular la inversa de $\mathbf{X}^{\prime} \mathbf{X}$, esto es análogo a dividir por cero en números escalares. Como regla general, cuando $VIF_j$ supera 10 (lo cual es equivalente a $R_j^2 > 90\%$), decimos que existe colinealidad severa. Esto puede indicar la necesidad de acción. Tolerancia, definida como el recíproco del factor de inflación de varianza, es otra medida de colinealidad utilizada por algunos analistas.

Por ejemplo, con $k = 2$ variables explicativas en el modelo, entonces $R_1^2$ es la correlación cuadrada entre las dos variables explicativas, digamos $r_{12}^2$. Entonces, a partir de la ecuación anterior, tenemos que

\[ se(b_j) = s \left(s_{x_j} \sqrt{n - 1} \right)^{-1} \left(1 - r_{12}^2 \right)^{-1/2}, \text{ para } j = 1, 2. \]

A medida que la correlación se acerca a uno en valor absoluto, $|r_{12}| \rightarrow 1$, entonces el error estándar se vuelve grande, lo que significa que el estadístico $t$ correspondiente se vuelve pequeño. En resumen, un alto $VIF$ puede significar pequeños estadísticos $t$ a pesar de que las variables sean importantes. Además, se puede verificar que la correlación entre $b_1$ y $b_2$ es $-r_{12}$, indicando que las estimaciones de los coeficientes están altamente correlacionadas.

Ejemplo: Liquidez del Mercado de Valores - Continuación. Como ejemplo, considere una regresión de VOLUME sobre PRICE, SHARE y VALUE. A diferencia de las variables explicativas consideradas en la Sección 5.5.3, estas tres variables explicativas no son medidas de actividad de trading. A partir de un ajuste de regresión, tenemos $R^2 = 61\%$ y $s = 6.72$. Las estadísticas asociadas con los coeficientes de regresión están en la Tabla 5.7.

Tabla 5.7: **Estadísticas de una regresión de VOLUME sobre PRICE, SHARE y VALUE**
$x_j$	$s_{x_j}$	$b_j$	$se(b_j)$	$t(b_j)$	$VIF_j$
PRICE	21.370	-0.022	0.035	-0.63	1.5
SHARE	115.100	0.054	0.010	5.19	3.8
VALUE	8.157	0.313	0.162	1.94	4.7

Puede verificar que la relación en la ecuación (5.5) es válida para cada una de las variables explicativas en la Tabla 5.7. Dado que cada estadístico $VIF$ es menor a diez, hay poca razón para sospechar colinealidad severa. Esto es interesante porque puede recordar que existe una relación perfecta entre PRICE, SHARE y VALUE en el sentido de que definimos el valor de mercado como VALUE = PRICE $\times$ SHARE. Sin embargo, la relación es multiplicativa y, por lo tanto, es no lineal. Debido a que las variables no están relacionadas linealmente, es válido incluir las tres en el modelo de regresión. Desde una perspectiva financiera, la variable VALUE es importante porque mide el valor de una empresa. Desde una perspectiva estadística, la variable VALUE cuantifica la interacción entre PRICE y SHARE (las variables de interacción se introdujeron en la Sección 3.5.3).

Para la colinealidad, solo nos interesa detectar tendencias lineales, por lo que las relaciones no lineales entre variables no son un problema aquí. Por ejemplo, hemos visto que a veces es útil mantener tanto una variable explicativa $x$ como su cuadrado $x^2$, a pesar de que existe una relación perfecta (no lineal) entre las dos. Sin embargo, debemos verificar que las relaciones no lineales no sean aproximadamente lineales en la región de muestreo. Aunque la relación es teóricamente no lineal, si es cercana a lineal para nuestra muestra disponible, pueden surgir problemas de colinealidad. La Figura 5.5 ilustra esta situación.

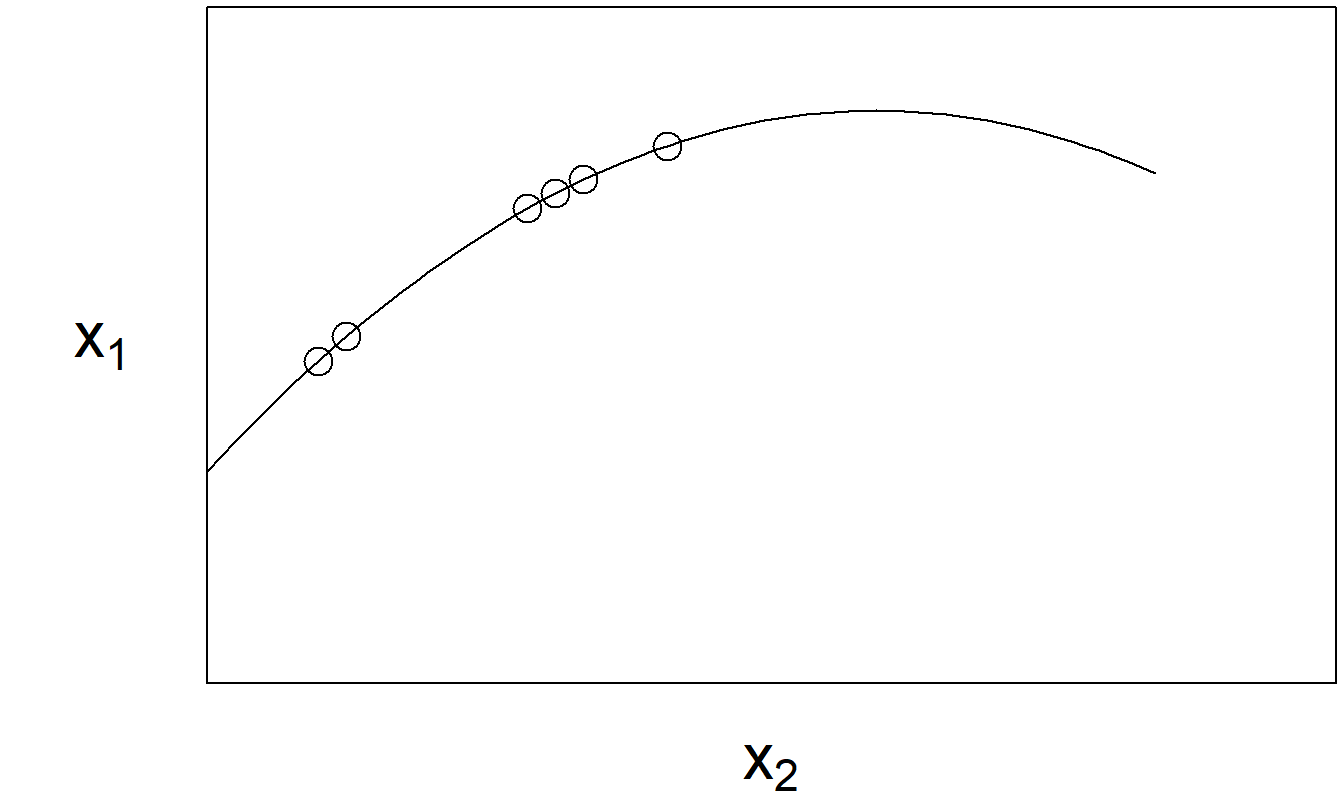
$La relación entre $x_1$ y $x_2$ es no lineal. Sin embargo, en la región muestreada, las variables tienen una relación casi lineal.$

Figura 5.5: La relación entre $x_1$ y $x_2$ es no lineal. Sin embargo, en la región muestreada, las variables tienen una relación casi lineal.

¿Qué podemos hacer en presencia de colinealidad? Una opción es centrar cada variable, restando su promedio y dividiendo por su desviación estándar. Por ejemplo, crear una nueva variable $x_{ij}^{\ast} = (x_{ij} - \bar{x}_j) / s_{x_j}$. A veces, una variable aparece en millones de unidades y otra en fracciones de unidades. Comparado con la primera variable, la segunda parece ser casi una columna constante de ceros (dado que las computadoras retienen típicamente un número finito de dígitos). Si esto es cierto, entonces la segunda variable se parece mucho a un desplazamiento lineal de la columna constante de unos correspondiente al intercepto. Esto es un problema porque, con las operaciones de mínimos cuadrados, estamos implícitamente elevando al cuadrado números que pueden hacer que estas columnas parezcan aún más similares.

Este problema es simplemente computacional y es fácil de corregir. Simplemente recodifique las variables para que las unidades sean de magnitud similar. Algunos analistas de datos centran automáticamente todas las variables para evitar estos problemas. Este es un enfoque legítimo porque las técnicas de regresión buscan relaciones lineales; los desplazamientos en ubicación y escala no afectan las relaciones lineales.

Otra opción es simplemente no tener en cuenta explícitamente la colinealidad en el análisis, pero discutir algunas de sus implicaciones al interpretar los resultados del análisis de regresión. Este enfoque es probablemente el más comúnmente adoptado. Es un hecho que, al tratar con datos de negocios y económicos, la colinealidad tiende a existir entre las variables. Dado que los datos tienden a ser observacionales en lugar de experimentales, hay poco que el analista pueda hacer para evitar esta situación.

En la mejor de las situaciones, una variable auxiliar que proporcione información similar y que facilite el problema de colinealidad está disponible para reemplazar una variable. Similar a nuestra discusión sobre puntos de alta influencia, una versión transformada de la variable explicativa también puede ser un sustituto útil. En algunas situaciones, un reemplazo ideal no está disponible y nos vemos obligados a eliminar una o más variables. Decidir qué variables eliminar es una elección difícil. Al decidir entre variables, a menudo la elección estará dictada por el juicio del investigador sobre cuál es el conjunto de variables más relevante.

5.5.3 Colinealidad e Influencia

Las medidas de colinealidad e influencia comparten características comunes y, sin embargo, están diseñadas para capturar diferentes aspectos de un conjunto de datos. Ambas son útiles para la crítica de datos y del modelo; se aplican después de un ajuste preliminar del modelo con el objetivo de mejorar la especificación del modelo. Además, ambas se calculan utilizando solo las variables explicativas; los valores de las respuestas no entran en ninguno de los cálculos.

Nuestra medida de colinealidad, el factor de inflación de la varianza, está diseñada para ayudar con la crítica del modelo. Es una medida calculada para cada variable explicativa, diseñada para explicar la relación con otras variables explicativas.

La estadística de influencia está diseñada para ayudarnos con la crítica de datos. Es una medida calculada para cada observación para ayudarnos a explicar cuán inusual es una observación con respecto a otras observaciones.

La colinealidad puede estar enmascarada o inducida por puntos de alta influencia, como lo señalaron Mason y Gunst (1985) y Hadi (1988). Las Figuras 5.6 y 5.7 proporcionan ilustraciones de cada caso. Estos ejemplos simples subrayan un punto importante: la crítica de datos y la crítica del modelo no son ejercicios separados.

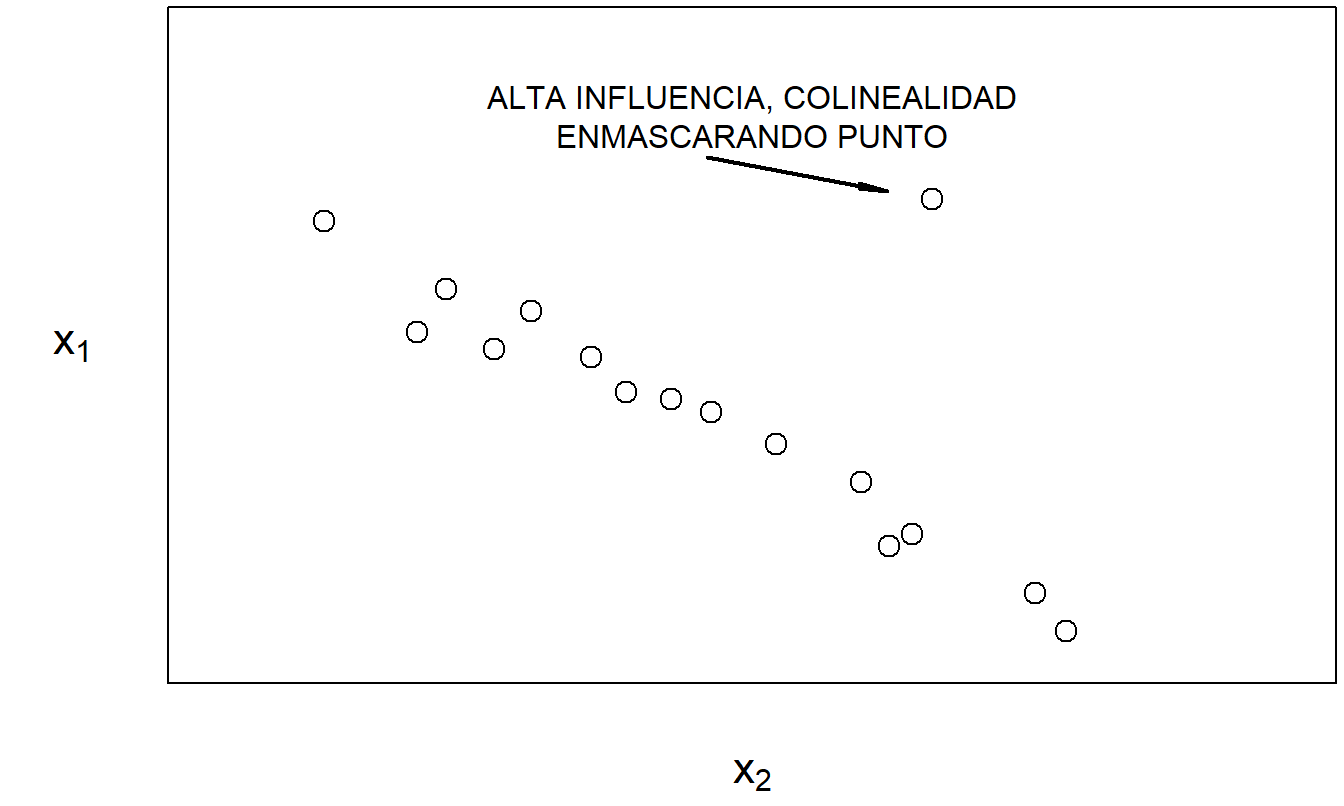
$Con la excepción del punto marcado, $x_1$ y $x_2$ están altamente relacionados linealmente.$

Figura 5.6: Con la excepción del punto marcado, $x_1$ y $x_2$ están altamente relacionados linealmente.

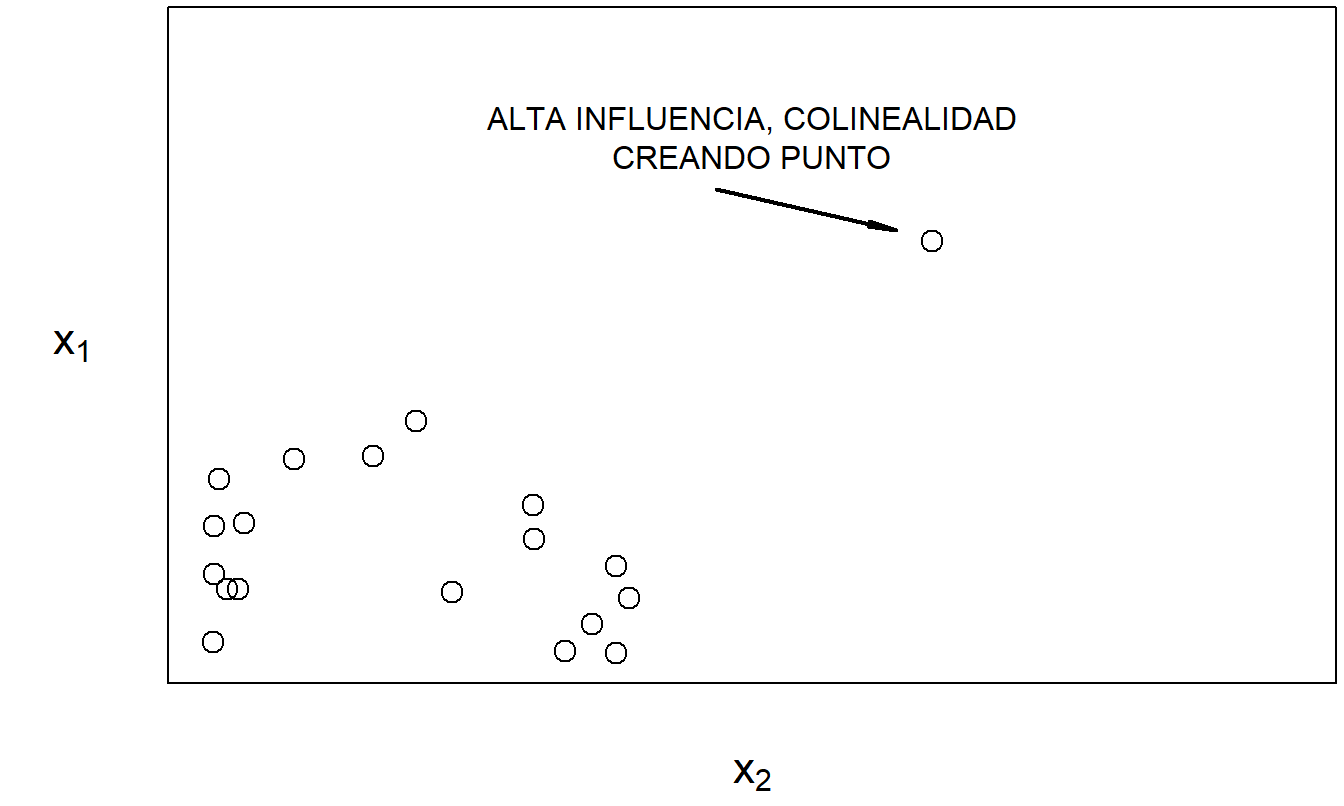
$La relación lineal altamente entre $x_1$ y $x_2$ es principalmente debido al punto marcado.$

Figura 5.7: La relación lineal altamente entre $x_1$ y $x_2$ es principalmente debido al punto marcado.

Los ejemplos en las Figuras 5.6 y 5.7 también nos ayudan a ver una forma en que los puntos de alta influencia pueden afectar los errores estándar de los coeficientes de regresión. Recuerde que, en la Sección 5.4.1, vimos que los puntos de alta influencia pueden afectar los valores ajustados del modelo. En las Figuras 5.6 y 5.7, vemos que los puntos de alta influencia afectan la colinealidad. Por lo tanto, a partir de la ecuación (5.5), tenemos que los puntos de alta influencia también pueden afectar nuestros errores estándar de los coeficientes de regresión.

5.5.4 Variables Suprensoras

Como hemos visto, la colinealidad severa puede inflar seriamente los errores estándar de los coeficientes de regresión. Dado que dependemos de estos errores estándar para evaluar la utilidad de las variables explicativas, nuestros procedimientos de selección de modelos e inferencias pueden ser deficientes en presencia de colinealidad severa. A pesar de estos inconvenientes, la colinealidad leve en un conjunto de datos no debe considerarse una deficiencia del conjunto de datos; es simplemente una característica de las variables explicativas disponibles.

Incluso si una variable explicativa es casi una combinación lineal de las demás, eso no significa necesariamente que la información que proporciona sea redundante. Para ilustrar, ahora consideramos una variable suprensora, una variable explicativa que aumenta la importancia de otras variables explicativas cuando se incluye en el modelo.

Ejemplo: Variable Suprensora. La Figura 5.8 muestra una matriz de dispersión de un conjunto de datos hipotético con cincuenta observaciones. Este conjunto de datos contiene una variable dependiente y dos variables explicativas. La Tabla 5.8 proporciona la matriz de coeficientes de correlación correspondiente. Aquí, vemos que las dos variables explicativas están altamente correlacionadas. Ahora recuerde que, para una regresión con una variable explicativa, el coeficiente de correlación al cuadrado es el coeficiente de determinación. Así, usando la Tabla 5.8, para una regresión de $y$ sobre $x_1$, el coeficiente de determinación es $(0.188)^2 = 3.5\%$. De manera similar, para una regresión de $y$ sobre $x_2$, el coeficiente de determinación es $(-0.022)^2 = 0.04\%$. Sin embargo, para una regresión de $y$ sobre $x_1$ y $x_2$, el coeficiente de determinación resulta ser sorprendentemente alto, $80.7\%$. La interpretación es que, individualmente, tanto $x_1$ como $x_2$ tienen poco impacto en $y$. Sin embargo, cuando se toman conjuntamente, las dos variables explicativas tienen un efecto significativo en $y$. Aunque la Tabla 5.8 muestra que $x_1$ y $x_2$ están fuertemente relacionados linealmente, esta relación no significa que $x_1$ y $x_2$ proporcionen la misma información. De hecho, en este ejemplo, las dos variables se complementan entre sí.

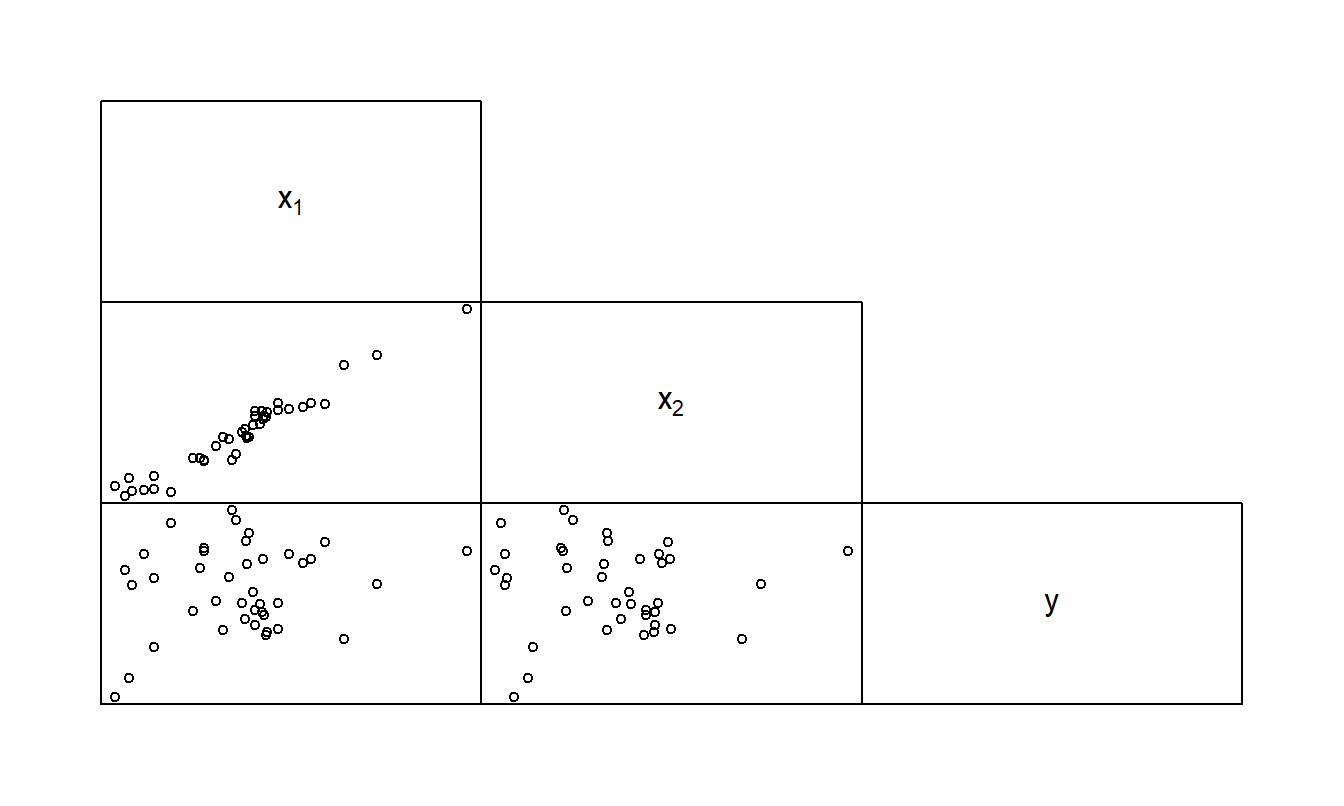
Figura 5.8: Matriz de dispersión de una variable dependiente y dos variables explicativas para el ejemplo de variable suprensora

Tabla 5.8: **Matriz de Correlación para el Ejemplo de Suprensor**
	$x_1$	$x_2$
$x_2$	0.972
$y$	0.188	-0.022

5.5.5 Variables Ortogonales

Otra forma de entender el impacto de la colinealidad es estudiar el caso en el que no hay relaciones entre conjuntos de variables explicativas. Matemáticamente, se dice que dos matrices $\mathbf{X}_1$ y $\mathbf{X}_2$ son ortogonales si $\mathbf{X}_1^{\prime} \mathbf{X}_2 = \mathbf{0}$. Intuitivamente, dado que generalmente trabajamos con variables centradas (con medias cero), esto significa que cada columna de $\mathbf{X}_1$ no está correlacionada con cada columna de $\mathbf{X}_2$. Aunque es poco probable que ocurra con datos observacionales en las ciencias sociales, al diseñar tratamientos experimentales o construir polinomios de alto grado, las aplicaciones de variables ortogonales se utilizan regularmente (véase, por ejemplo, Hocking, 2003). Para nuestros propósitos, trabajaremos con variables ortogonales simplemente para entender las consecuencias lógicas de una ausencia total de colinealidad.

Supongamos que $\mathbf{x}_2$ es una variable explicativa que es ortogonal a $\mathbf{X}_1$, donde $\mathbf{X}_1$ es una matriz de variables explicativas que incluye la intersección. Entonces, es sencillo comprobar que la adición de $\mathbf{x}_2$ a la ecuación de regresión no cambia el ajuste para los coeficientes correspondientes a $\mathbf{X}_1$. Es decir, sin $\mathbf{x}_2$, los coeficientes correspondientes a $\mathbf{X}_1$ se calcularían como $\mathbf{b}_1 = \left(\mathbf{X}_1^{\prime} \mathbf{X}_1 \right)^{-1} \mathbf{X}_1^{\prime} \mathbf{y}$. Usar el ortogonal $\mathbf{x}_2$ como parte del cálculo de mínimos cuadrados no cambiaría el resultado para $\mathbf{b}_1$ (véase el cálculo recursivo de mínimos cuadrados en la Sección 4.7.2).

Además, el factor de inflación de la varianza para $\mathbf{x}_2$ es 1, lo que indica que el error estándar no se ve afectado por las otras variables explicativas. De manera similar, la reducción en la suma de errores al agregar la variable ortogonal $\mathbf{x}_2$ se debe únicamente a esa variable, y no a su interacción con otras variables en $\mathbf{X}_1$.

Las variables ortogonales pueden ser creadas para datos observacionales en ciencias sociales (así como otros datos colineales) utilizando el método de componentes principales. Con este método, se utiliza una transformación lineal de la matriz de variables explicativas de la forma, $\mathbf{X}^{\ast} = \mathbf{X} \mathbf{P}$, de manera que la matriz resultante $\mathbf{X}^{\ast}$ esté compuesta por columnas ortogonales. La función de regresión transformada es $\mathrm{E~}\mathbf{y} = \mathbf{X} \boldsymbol \beta = \mathbf{X} \mathbf{P} \mathbf{P}^{-1} \boldsymbol \beta = \mathbf{X}^{\ast} \boldsymbol \beta^{\ast}$, donde $\boldsymbol \beta^{\ast} = \mathbf{P}^{-1} \boldsymbol \beta$ es el conjunto de nuevos coeficientes de regresión. La estimación procede como antes, con el conjunto ortogonal de variables explicativas. Al elegir la matriz $\mathbf{P}$ apropiadamente, cada columna de $\mathbf{X}^{\ast}$ tiene una contribución identificable. Así, podemos usar técnicas de selección de variables para identificar las porciones de “componentes principales” de $\mathbf{X}^{\ast}$ para usar en la ecuación de regresión. La regresión por componentes principales es un método ampliamente utilizado en algunas áreas de aplicación, como la psicología. Puede abordar fácilmente datos altamente colineales de manera disciplinada. La principal desventaja de esta técnica es que las estimaciones de parámetros resultantes son difíciles de interpretar.

5.6 Criterios de Selección

5.6.1 Bondad de Ajuste

¿Qué tan bien se ajusta el modelo a los datos? Los criterios que miden la proximidad entre el modelo ajustado y los datos reales se conocen como estadísticas de bondad de ajuste. Específicamente, interpretamos el valor ajustado $\hat{y}_i$ como la mejor aproximación del modelo para la $i$-ésima observación y lo comparamos con el valor real $y_i$. En la regresión lineal, examinamos la diferencia a través del residuo $e_i = y_i - \hat{y}_i$; residuos pequeños implican un buen ajuste del modelo. Hemos cuantificado esto a través del tamaño del error típico $(s)$, incluyendo el coeficiente de determinación $(R^2)$ y una versión ajustada $(R_{a}^2)$.

Para modelos no lineales, necesitaremos medidas adicionales, y es útil introducir estas medidas en este caso lineal más simple. Una de estas medidas es el Criterio de Información de Akaike que se definirá en términos de ajustes de verosimilitud en la Sección 11.9.4. Para la regresión lineal, se reduce a

\[\begin{equation} AIC = n \ln (s^2) + n \ln (2 \pi) + n + 3 + k. \tag{5.6} \end{equation}\]

Para la comparación de modelos, cuanto menor sea el $AIC$, mejor es el ajuste. Comparar modelos con el mismo número de variables ($k$) significa que seleccionar un modelo con valores bajos de $AIC$ lleva a la misma elección que seleccionar un modelo con valores bajos de la desviación estándar de los residuos $s$. Además, un pequeño número de parámetros implica un valor bajo de $AIC$, manteniéndose todo lo demás constante. La idea es que esta medida equilibra el ajuste ($n \ln (s^2)$) con una penalización por complejidad (el número de parámetros, $k+2$). Los paquetes estadísticos a menudo omiten constantes como $n \ln (2 \pi)$ y $n+3$ al reportar $AIC$ porque no importan al comparar modelos.

La Sección 11.9.4 presentará otra medida, el Criterio de Información de Bayes ($BIC$), que da un peso menor a la penalización por complejidad. Una tercera medida de bondad de ajuste que se usa en modelos de regresión lineal es la estadística $C_p$. Para definir esta estadística, supongamos que tenemos disponibles $k$ variables explicativas $x_1, ..., x_{k}$ y realizamos una regresión para obtener $s_{full}^2$ como el error cuadrático medio. Ahora, supongamos que consideramos usar solo $p-1$ variables explicativas de modo que haya $p$ coeficientes de regresión. Con estas $p-1$ variables explicativas, realizamos una regresión para obtener la suma de cuadrados del error $(Error~SS)_p$. Así, estamos en posición de definir

\[ C_{p} = \frac{(Error~SS)_p}{s_{full}^2} - n + 2p. \]

Como criterio de selección, elegimos el modelo con un coeficiente $C_{p}$ “pequeño”, donde pequeño se entiende en relación con $p$. En general, los modelos con valores más pequeños de $C_{p}$ son más deseables.

Al igual que las estadísticas $AIC$ y $BIC$, la estadística $C_{p}$ busca un equilibrio entre el ajuste del modelo y la complejidad. Es decir, cada estadística resume el compromiso entre el ajuste del modelo y la complejidad, aunque con diferentes pesos. Para la mayoría de los conjuntos de datos, recomiendan el mismo modelo, por lo que un analista puede reportar cualquiera o todas las tres estadísticas. Sin embargo, para algunas aplicaciones, llevan a diferentes modelos recomendados. En este caso, el analista necesita confiar más en criterios no basados en datos para la selección del modelo (los cuales siempre son importantes en cualquier aplicación de regresión).

5.6.2 Validación del Modelo

La validación del modelo es el proceso de confirmar que nuestro modelo propuesto es apropiado, especialmente a la luz de los propósitos de la investigación. Recuerda el proceso iterativo de formulación y selección de modelos descrito en la Sección 5.1. Una crítica importante a este proceso iterativo es que es culpable de búsqueda de datos, es decir, ajustar un gran número de modelos a un solo conjunto de datos. Como vimos en la Sección 5.2 sobre la búsqueda de datos en la regresión paso a paso, al mirar una gran cantidad de modelos podemos sobreajustar los datos y subestimar la variación natural en nuestra representación.

Podemos responder a esta crítica utilizando una técnica llamada validación fuera de muestra. La situación ideal es tener disponibles dos conjuntos de datos, uno para el desarrollo del modelo y otro para la validación del modelo. Inicialmente desarrollamos uno o varios modelos en el primer conjunto de datos. Los modelos desarrollados a partir del primer conjunto de datos se llaman nuestros modelos candidatos. Luego, el rendimiento relativo de los modelos candidatos podría medirse en un segundo conjunto de datos. De esta manera, los datos utilizados para validar el modelo no se ven afectados por los procedimientos utilizados para formular el modelo.

Desafortunadamente, rara vez estarán disponibles dos conjuntos de datos para el investigador. Sin embargo, podemos implementar el proceso de validación dividiendo el conjunto de datos en dos submuestras. A estas las llamamos las submuestras de desarrollo del modelo y submuestras de validación, respectivamente. También se conocen como muestras de entrenamiento y prueba, respectivamente. Para ver cómo funciona el proceso en el contexto de la regresión lineal, considera el siguiente procedimiento.

Procedimiento de Validación Fuera de Muestra

Comienza con un tamaño de muestra de $n$ y divídelo en dos submuestras, llamadas la submuestra de desarrollo del modelo y la submuestra de validación. Sea $n_1$ y $n_2$ el tamaño de cada submuestra. En regresión transversal, realiza esta división usando un mecanismo de muestreo aleatorio. Usa la notación $i=1,...,n_1$ para representar las observaciones de la submuestra de desarrollo del modelo y $i=n_1+1,...,n_1+n_2=n$ para las observaciones de la submuestra de validación. La Figura 5.9 ilustra este procedimiento.
Usando la submuestra de desarrollo del modelo, ajusta un modelo candidato al conjunto de datos $i=1,...,n_1$.
Usando el modelo creado en el Paso (ii) y las variables explicativas de la submuestra de validación, “predice” las variables dependientes en la submuestra de validación, $\hat{y}_i$, donde $i=n_1+1,...,n_1+n_2$. (Para obtener estas predicciones, puede que necesites transformar las variables dependientes de nuevo a la escala original.)
Evalúa la proximidad de las predicciones a los datos retenidos. Una medida es la suma de errores cuadráticos de predicción \[\begin{equation} SSPE = \sum_{i=n_1+1}^{n_1+n_2} (y_i - \hat{y}_i)^2 . \tag{5.7} \end{equation}\] Repite los Pasos (ii) a (iv) para cada modelo candidato. Elige el modelo con el menor SSPE.

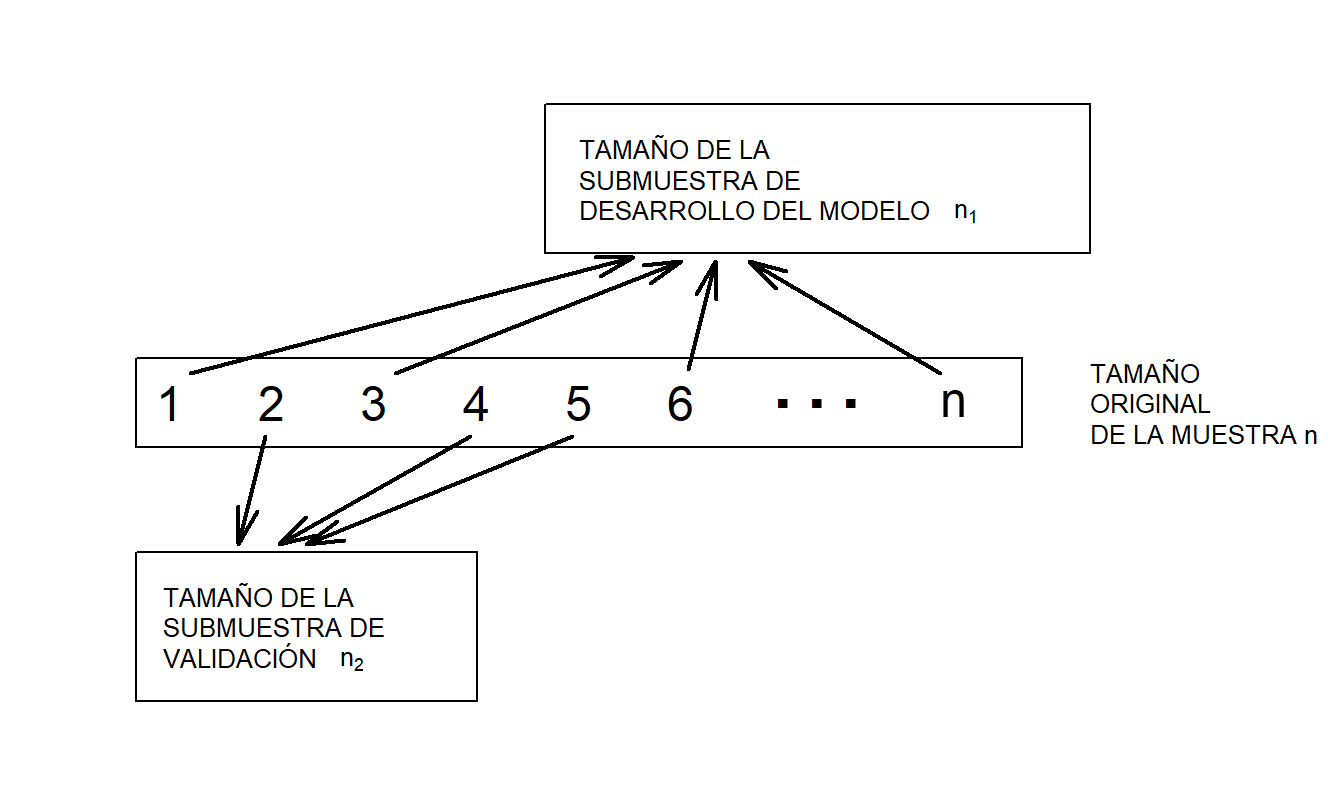
$Para la validación del modelo, un conjunto de datos de tamaño $n$ se divide aleatoriamente en dos submuestras$

Figura 5.9: Para la validación del modelo, un conjunto de datos de tamaño $n$ se divide aleatoriamente en dos submuestras

Existen varias críticas a la SSPE. Primero, es evidente que calcular esta estadística para cada uno de varios modelos candidatos lleva una cantidad considerable de tiempo y esfuerzo. Sin embargo, como ocurre con muchas técnicas estadísticas, esto es simplemente una cuestión de tener disponible software estadístico especializado para realizar los pasos descritos anteriormente. Segundo, dado que la estadística en sí se basa en un subconjunto aleatorio de la muestra, su valor variará de un analista a otro. Esta objeción podría superarse utilizando las primeras $n_1$ observaciones de la muestra. En la mayoría de las aplicaciones, esto no se hace por si hay una relación oculta en el orden de las observaciones. Tercero, y quizás lo más importante, es el hecho de que la elección de los tamaños relativos de los subconjuntos, $n_1$ y $n_2$, no está clara. Varios investigadores recomiendan diferentes proporciones para la asignación. Snee (1977) sugiere que la división de datos no se realice a menos que el tamaño de la muestra sea moderadamente grande, específicamente, $n \geq 2(k+1) + 20$. Las directrices de Picard y Berk (1990) muestran que cuanto mayor es el número de parámetros a estimar, mayor es la proporción de observaciones necesarias para la submuestra de desarrollo del modelo. Como regla general, para conjuntos de datos con 100 observaciones o menos, usa alrededor del 25-35% de la muestra para validación fuera de muestra. Para conjuntos de datos con 500 o más observaciones, usa el 50% de la muestra para validación fuera de muestra. Hastie, Tibshirani y Friedman (2001) señalan que una división típica es 50% para desarrollo/entrenamiento, 25% para validación, y el 25% restante para una tercera etapa de validación adicional que ellos llaman prueba.

Debido a estas críticas, los analistas utilizan varias variantes del proceso básico de validación fuera de muestra. Aunque no existe un procedimiento teóricamente mejor, se acuerda ampliamente que la validación del modelo es una parte importante para confirmar la utilidad de un modelo.

5.6.3 Validación Cruzada

La validación cruzada es una técnica de validación de modelos que divide los datos en dos conjuntos disjuntos. La Sección 5.6.2 discutió la validación fuera de muestra, donde los datos se dividieron aleatoriamente en dos subconjuntos, ambos conteniendo un porcentaje considerable de los datos. Otro método popular es la validación cruzada de dejar uno fuera, donde la muestra de validación consiste en una sola observación y la muestra de desarrollo se basa en el resto del conjunto de datos.

Especialmente para tamaños de muestra pequeños, una estadística atractiva de validación cruzada de dejar uno fuera es PRESS, la Suma de Cuadrados de Residuos Predichos. Para definir la estadística, considera el siguiente procedimiento donde suponemos que hay un modelo candidato disponible.

Procedimiento de Validación PRESS

Desde la muestra completa, omite el $i$-ésimo punto y usa las $n-1$ observaciones restantes para calcular los coeficientes de regresión.
Usa los coeficientes de regresión calculados en el primer paso y las variables explicativas para la $i$-ésima observación para calcular la respuesta predicha, $\hat{y}_{(i)}$. Esta parte del procedimiento es similar al cálculo de la estadística SSPE con $n_1=n-1$ y $n_2=1$.
Ahora, repite (i) y (ii) para $i=1,...,n$. Resumiendo, define \[\begin{equation} PRESS = \sum_{i=1}^{n} (y_i - \hat{y}_{(i)})^2 . \tag{5.8} \end{equation}\] Al igual que con SSPE, esta estadística se calcula para cada uno de varios modelos competidores. Bajo este criterio, elegimos el modelo con el PRESS más pequeño.

Basado en esta definición, la estadística parece ser muy intensiva en cálculos ya que requiere $n$ ajustes de regresión para evaluarla. Para abordar esto, los lectores interesados encontrarán que la Sección 5.10.2 establece

\[\begin{equation} y_i - \hat{y}_{(i)} = \frac{e_i}{1 - h_{ii}} . \tag{5.9} \end{equation}\]

Aquí, $e_i$ y $h_{ii}$ representan el $i$-ésimo residuo y la influencia del ajuste de regresión utilizando el conjunto de datos completo. Esto da lugar a

\[\begin{equation} PRESS = \sum_{i=1}^{n} \left( \frac{e_i}{1 - h_{ii}} \right)^2 , \tag{5.10} \end{equation}\]

lo cual es una fórmula computacionalmente mucho más fácil. Así, la estadística PRESS es menos intensiva en cálculos que SSPE.

Otra ventaja importante de esta estadística, en comparación con SSPE, es que no necesitamos hacer una elección arbitraria sobre los tamaños relativos de los subconjuntos. De hecho, dado que estamos realizando una validación “fuera de muestra” para cada observación, se puede argumentar que este procedimiento es más eficiente, una consideración especialmente importante cuando el tamaño de la muestra es pequeño (por ejemplo, menos de 50 observaciones). Una desventaja es que, dado que el modelo se vuelve a ajustar para cada punto eliminado, PRESS no goza de la apariencia de independencia entre los aspectos de estimación y predicción, a diferencia de SSPE.

5.7 Heterocedasticidad

En la mayoría de las aplicaciones de regresión, el objetivo es entender los determinantes de la función de regresión $\mathrm{E~}y_i = \mathbf{x}_i^{\prime} \boldsymbol \beta = \mu_i$. Nuestra capacidad para entender la media está fuertemente influenciada por la cantidad de dispersión respecto a la media, que cuantificamos usando la varianza $\mathrm{E}\left(y_i - \mu_i\right)^2$. En algunas aplicaciones, como cuando me peso en una balanza, hay relativamente poca variabilidad; las mediciones repetidas dan casi el mismo resultado. En otras aplicaciones, como el tiempo que me toma volar a Nueva York, las mediciones repetidas muestran una variabilidad sustancial y están llenas de incertidumbre inherente.

La cantidad de incertidumbre también puede variar de un caso a otro. Denotamos el caso de “variabilidad variable” con la notación $\sigma_i^2 = \mathrm{E}\left(y_i - \mu_i\right)^2$. Cuando la variabilidad varía según la observación, esto se conoce como heterocedasticidad, que significa “dispersión diferente”. En contraste, la suposición habitual de variabilidad común (suposición E3/F3 en la Sección 3.2) se llama homocedasticidad, lo que significa “misma dispersión”.

Nuestras estrategias de estimación dependen del grado de heterocedasticidad. Para conjuntos de datos con solo una ligera heterocedasticidad, se puede usar mínimos cuadrados para estimar los coeficientes de regresión, tal vez combinado con un ajuste para los errores estándar (descritos en la Sección 5.7.2). Esto se debe a que los estimadores de mínimos cuadrados son insesgados incluso en presencia de heterocedasticidad (ver Propiedad 1 en la Sección 3.2).

Sin embargo, con variables dependientes heterocedásticas, el teorema de Gauss-Markov ya no se aplica, por lo que los estimadores de mínimos cuadrados no están garantizados como óptimos. En casos de heterocedasticidad severa, se utilizan estimadores alternativos, siendo los más comunes aquellos basados en transformaciones de la variable dependiente, como se describirá en la Sección 5.7.4.

5.7.1 Detección de Heterocedasticidad

Para decidir una estrategia para manejar la posible heterocedasticidad, primero debemos evaluar o detectar su presencia.

Para detectar heterocedasticidad de manera gráfica, una buena idea es realizar un ajuste preliminar de regresión de los datos y trazar los residuos frente a los valores ajustados. Para ilustrar, la Figura 5.10 muestra un gráfico de un conjunto de datos ficticio con una variable explicativa donde la dispersión aumenta a medida que aumenta la variable explicativa. Se realizó una regresión por mínimos cuadrados: se calcularon los residuos y los valores ajustados. La Figura 5.11 es un ejemplo de un gráfico de residuos frente a valores ajustados. El ajuste preliminar de regresión elimina muchos de los patrones principales en los datos y deja al ojo libre para concentrarse en otros patrones que pueden influir en el ajuste. Trazamos los residuos frente a los valores ajustados porque los valores ajustados son una aproximación del valor esperado de la respuesta y, en muchas situaciones, la variabilidad crece con la respuesta esperada.

Figura 5.10: El área sombreada representa los datos.

Figura 5.11: Residuos trazados frente a los valores ajustados para los datos en la Figura 5.10.

Más pruebas formales de heterocedasticidad también están disponibles en la literatura de regresión. Por ejemplo, consideremos una prueba de Breusch y Pagan (1980). Específicamente, esta prueba examina la hipótesis alternativa $H_a$: $ y_i = ^2 + _i^{} $, donde $\mathbf{z}_i$ es un vector conocido de variables y $\boldsymbol \gamma$ es un vector de parámetros de dimensión $p$. Así, la hipótesis nula es $H_0:~ \boldsymbol \gamma = \mathbf{0}$, que es equivalente a homocedasticidad, $\mathrm{Var~} y_i = \sigma^2.$

Procedimiento para la Prueba de Heterocedasticidad

Ajuste un modelo de regresión y calcule los residuos del modelo, $e_i$.
Calcule los residuos estandarizados al cuadrado, $e_i^{\ast 2} = e_i^2 / s^2$.
Ajuste un modelo de regresión de $e_i^{\ast 2}$ sobre $\mathbf{z}_i$.
La estadística de la prueba es $LM = \frac{\text{Regress~SS}_z}{2}$, donde $Regress~SS_z$ es la suma de cuadrados de la regresión del ajuste del modelo en el paso (iii).
Rechace la hipótesis nula si $LM$ excede un percentil de una distribución chi-cuadrado con $p$ grados de libertad. El percentil es uno menos el nivel de significancia de la prueba.

Aquí usamos $LM$ para denotar la estadística de la prueba porque Breusch y Pagan la derivaron como una estadística de multiplicador de Lagrange; consulte Breusch y Pagan (1980) para más detalles.

5.7.2 Errores Estándar Consistentes con Heterocedasticidad

Para conjuntos de datos con solo una leve heterocedasticidad, una estrategia sensata es emplear estimadores de mínimos cuadrados de los coeficientes de regresión y ajustar el cálculo de errores estándar para tener en cuenta la heterocedasticidad.

En la Sección 3.2 sobre propiedades, vimos que los coeficientes de regresión por mínimos cuadrados pueden escribirse como $\mathbf{b} = \sum_{i=1}^n \mathbf{w}_i y_i,$ donde $\mathbf{w}_i = \left( \mathbf{X}^{\prime}\mathbf{X} \right)^{-1} \mathbf{x}_i$. Así, con $\sigma_i^2 = \mathrm{Var~} y_i$, tenemos \[\begin{equation} \mathrm{Var~}\mathbf{b} = \sum_{i=1}^n \mathbf{w}_i \mathbf{w}_i^{\prime} \sigma_i^2 = \left( \mathbf{X}^{\prime}\mathbf{X} \right)^{-1} \left( \sum_{i=1}^n \sigma_i^2 \mathbf{x}_i \mathbf{x}_i^{\prime} \right) \left( \mathbf{X}^{\prime}\mathbf{X} \right)^{-1}. \tag{5.11} \end{equation}\] Esta cantidad es conocida excepto por $\sigma_i^2$. Podemos calcular los residuos usando los coeficientes de regresión por mínimos cuadrados como $e_i = y_i - \mathbf{x}_i^{\prime} \mathbf{b}$. Con estos, podemos definir la estimación empírica, o robusta, de la matriz varianza-covarianza como \[ \widehat{\mathrm{Var~}\mathbf{b}} = \left( \mathbf{X}^{\prime}\mathbf{X} \right)^{-1} \left( \sum_{i=1}^n e_i^2 \mathbf{x}_i \mathbf{x}_i^{\prime} \right) \left( \mathbf{X}^{\prime}\mathbf{X} \right)^{-1}. \] Los correspondientes errores estándar “consistentes con heterocedasticidad” son \[\begin{equation} se_r(b_j) = \sqrt{(j+1)^{\text{er}}~ \text{elemento diagonal de }\widehat{\mathrm{Var~}\mathbf{b}}}. \tag{5.12} \end{equation}\] La lógica detrás de este estimador es que cada residual al cuadrado, $e_i^2$, puede ser una mala estimación de $\sigma_i^2$. Sin embargo, nuestro interés es estimar una (ponderada) suma de varianzas en la ecuación (5.11); estimar la suma es una tarea mucho más fácil que estimar cualquier estimación de varianza individual.

Los errores estándar robustos, o consistentes con heterocedasticidad, están ampliamente disponibles en paquetes de software estadístico. Aquí, también verá definiciones alternativas de residuos empleados, como en la Sección 5.3.1. Si su paquete estadístico ofrece opciones, el estimador robusto que utiliza residuos studentizados es generalmente preferido.

5.7.3 Mínimos Cuadrados Ponderados

Los estimadores de mínimos cuadrados son menos útiles para conjuntos de datos con heterocedasticidad severa. Una estrategia es usar una variación de la estimación por mínimos cuadrados mediante el ponderado de las observaciones. La idea es que, al minimizar la suma de errores cuadrados usando datos heterocedásticos, la variabilidad esperada de algunas observaciones es menor que la de otras. Intuitivamente, parece razonable que, cuanto menor es la variabilidad de la respuesta, más confiable es esa respuesta y mayor peso debería recibir en el procedimiento de minimización. Los mínimos cuadrados ponderados son una técnica que tiene en cuenta esta “variabilidad variable”.

Específicamente, usamos los supuestos E1, E2 y E4 de la Sección 3.2.3, con E3 reemplazado por E $\varepsilon_i = 0$ y $\text{Var} \varepsilon_i = \sigma^2 / w_i$, de modo que la variabilidad es proporcional a un peso conocido $w_i$. Por ejemplo, si la unidad de análisis $i$ representa una entidad geográfica como un estado, podrías usar el número de personas en el estado como peso. O, si $i$ representa una empresa, podrías usar los activos de la empresa para la variable de ponderación. Valores mayores de $w_i$ indican una variable de respuesta más precisa a través de una menor variabilidad. En aplicaciones actuariales, se usan pesos para tener en cuenta una exposición, como el monto de la prima de seguro, el número de empleados, el tamaño de la nómina, el número de vehículos asegurados, etc. (una discusión más detallada está en el Capítulo 18).

Este modelo puede convertirse fácilmente en el problema de “mínimos cuadrados ordinarios” multiplicando todas las variables de regresión por $\sqrt{w_i}$. Es decir, si definimos $y_i^{\ast} = y_i \times \sqrt{w_i}$ y $x_{ij}^{\ast} = x_{ij} \times \sqrt{w_i}$, entonces, a partir del supuesto E1, tenemos \[ \begin{array}{ll} y_i^{\ast} & = y_i \times \sqrt{w_i} = \left( \beta_0 x_{i0} + \beta_1 x_{i1} + \ldots + \beta_k x_{ik} + \varepsilon_i \right) \sqrt{w_i} \\ &= \beta_0 x_{i0}^{\ast} + \beta_1 x_{i1}^{\ast} + \ldots + \beta_k x_{ik}^{\ast} + \varepsilon_i^{\ast} \end{array} \] donde $\varepsilon_i^{\ast} = \varepsilon_i \times \sqrt{w_i}$ tiene una varianza homocedástica $\sigma^2$. Así, con las variables reescaladas, toda la inferencia puede proceder como antes.

Este trabajo ha sido automatizado en paquetes estadísticos donde el usuario simplemente especifica los pesos $w_i$ y el paquete hace el resto. En términos de álgebra de matrices, este procedimiento se puede llevar a cabo definiendo una matriz de pesos $n \times n$ $\mathbf{W} = \text{diag}(w_i)$, de modo que el elemento diagonal $i$-ésimo de $\mathbf{W}$ sea $w_i$. Ampliando la ecuación (3.14), por ejemplo, las estimaciones de mínimos cuadrados ponderados se pueden expresar como \[\begin{equation} \mathbf{b}_{WLS} = \left( \mathbf{X}^{\prime} \mathbf{W} \mathbf{X} \right)^{-1} \mathbf{X}^{\prime} \mathbf{W} \mathbf{y}. \tag{5.13} \end{equation}\] Discuciones adicionales sobre la estimación de mínimos cuadrados ponderados se presentarán en la Sección 15.1.1.

5.7.4 Transformaciones

Otro enfoque que maneja la heterocedasticidad severa, introducido en la Sección 1.3, es transformar la variable dependiente, típicamente con una transformación logarítmica de la forma $y^{\ast} = \ln y$. Como vimos en la Sección 1.3, las transformaciones pueden servir para “reducir” la dispersión de los datos y simetrizar una distribución. A través de un cambio de escala, una transformación también cambia la variabilidad, potencialmente alterando un conjunto de datos heterocedástico en uno homocedástico. Esta es tanto una fortaleza como una limitación del enfoque de transformación: una transformación afecta simultáneamente tanto la distribución como la heterocedasticidad.

Las transformaciones de potencia, como la transformación logarítmica, son más útiles cuando la variabilidad de los datos crece con la media. En este caso, la transformación servirá para “reducir” los datos a una escala que parece ser homocedástica. Por el contrario, dado que las transformaciones son funciones monótonas, no ayudarán con patrones de variabilidad que son no monótonos. Además, si tus datos son razonablemente simétricos pero heterocedásticos, una transformación no será útil porque cualquier elección que mitigue la heterocedasticidad sesgará la distribución.

Cuando los datos no son positivos, es común agregar una constante a cada observación para que todas las observaciones sean positivas antes de la transformación. Por ejemplo, la transformación $\ln(1+y)$ acomoda la presencia de ceros. También se puede multiplicar por una constante para que se mantengan las unidades originales aproximadas. Por ejemplo, la transformación $100 \ln(1 + y/100)$ puede aplicarse a datos porcentuales donde a veces aparecen porcentajes negativos.

Nuestras discusiones sobre transformaciones se han centrado en transformar variables dependientes. Como se señaló en la Sección 3.5, también es posible transformar variables explicativas. Esto se debe a que los supuestos de regresión condicionan las variables explicativas (Sección 3.2.3). Algunos analistas prefieren transformar variables para aproximarse a la normalidad, considerando las distribuciones normales multivariadas como una base para el análisis de regresión. Otros son reacios a transformar variables explicativas debido a las dificultades para interpretar los modelos resultantes. El enfoque aquí es usar transformaciones que sean fácilmente interpretables, como las introducidas en la Sección 3.5. Otras transformaciones son ciertamente candidatas para incluir en un modelo seleccionado, pero deben proporcionar dividendos sustanciales en términos de ajuste o poder predictivo si son difíciles de comunicar.

5.8 Lectura Adicional y Referencias

Long y Ervin (2000) reúnen pruebas convincentes sobre el uso de estimadores alternativos consistentes con la heterocedasticidad para los errores estándar que tienen un mejor rendimiento en muestras finitas que las versiones clásicas. Las propiedades de gran muestra de los estimadores empíricos han sido establecidas por Eicker (1967), Huber (1967) y White (1980) en el caso de la regresión lineal. Para el caso de la regresión lineal, MacKinnon y White (1985) sugieren alternativas que proporcionan mejores propiedades en muestras pequeñas. Para muestras pequeñas, la evidencia se basa en (1) el sesgo de los estimadores, (2) su motivación como estimadores jackknife y (3) su rendimiento en estudios de simulación.

Otros métodos para medir la colinealidad basados en conceptos de álgebra de matrices que involucran valores propios, como los números de condición y los índices de condición, son utilizados por algunos analistas. Consulta a Belsey, Kuh y Welsch (1980) para un tratamiento sólido de la colinealidad y los diagnósticos de regresión. Hocking (2003) proporciona lecturas adicionales sobre colinealidad y componentes principales. Consulta a Carroll y Ruppert (1988) para más discusiones sobre transformaciones en la regresión.

Hastie, Tibshirani y Friedman (2001) ofrecen una discusión avanzada sobre problemas de selección de modelos, centrándose en los aspectos predictivos de los modelos en el lenguaje del aprendizaje automático.

Referencias del Capítulo

Belseley, David A., Edwin Kuh and Roy E. Welsch (1980). Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. Wiley, New York.
Bendel, R. B. and Afifi, A. A. (1977). Comparison of stopping rules in forward “stepwise” regression. Journal of the American Statistical Association 72, 46-53.
Box, George E. P. (1980). Sampling and Bayes inference in scientific modeling and robustness (with discussion). Journal of the Royal Statistical Society, Series A, 143, 383-430.
Breusch, T. S. and A. R. Pagan (1980). The Lagrange multiplier test and its applications to model specification in econometrics. Review of Economic Studies, 47, 239-53.
Carroll, Raymond J. and David Ruppert (1988). Transformation and Weighting in Regression, Chapman-Hall.
Eicker, F. (1967). Limit theorems for regressions with unequal and dependent errors. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability 1, LeCam, L. M. and J. Neyman, editors, University of California Press, pp, 59-82.
Hadi, A. S. (1988). Diagnosing collinearity-influential observations. Computational Statistics and Data Analysis 7, 143-159.
Hastie, Trevor, Robert Tibshirani and Jerome Friedman (2001). The Elements of Statistical Learning: Data Mining, Inference and Prediction. Springer-Verlag, New York.
Hocking, Ronald R. (2003). Methods and Applications of Linear Models: Regression and the Analysis of Variance. Wiley, New York.
Huber, P. J. (1967). The behaviour of maximum likelihood estimators under non-standard conditions. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability 1, LeCam, L. M. and Neyman, J. editors, University of California Press, pp, 221-33.
Long, J.S. and L.H. Ervin (2000). Using heteroscedasticity consistent standard errors in the linear regression model. American Statistician 54, 217-224.
MacKinnon, J.G. and H. White (1985). Some heteroskedasticity consistent covariance matrix estimators with improved finite sample properties. Journal of Econometrics 29, 53-57.
Mason, R. L. and Gunst, R. F. (1985). Outlier-induced collinearities. Technometrics 27, 401-407.
Picard, R. R. and Berk, K. N. (1990). Data splitting. The American Statistician 44, 140-147.
Rencher, A. C. and Pun, F. C. (1980). Inflation of $R^2$ in best subset regression. Technometrics 22, 49-53.
Snee, R. D. (1977). Validation of regression models. Methods and examples. Technometrics 19, 415-428.

5.9 Ejercicios

5.1. Estás realizando una regresión con una variable explicativa, por lo que considera el modelo de regresión lineal básico $y_i = \beta_0 + \beta_1 x_i + \varepsilon_i$.

Muestra que el apalancamiento $i$-ésimo se puede simplificar a \[ h_{ii} = \frac{1}{n} + \frac{(x_i - \overline{x})^2}{(n-1) s_x^2}. \]
Muestra que $\overline{h} = 2 / n$.
Supón que $h_{ii} = 6/n$. ¿Cuántas desviaciones estándar está $x_i$ alejado (ya sea por encima o por debajo) de la media?

5.2. Considera los resultados de una regresión usando una variable explicativa con $n=3$ observaciones. Los residuos y los apalancamientos son: \[ \small{ \begin{array}{l|ccc} \hline i & 1 & 2 & 3 \\ \hline \text{Residuos } e_i & 3.181 & -6.362 & 3.181 \\ \text{Apalancamientos } h_{ii} & 0.8333 & 0.3333 & 0.8333 \\ \hline \end{array} } \]

Calcula el estadístico $PRESS$.

5.3. Expectativas de Vida Nacionales. Continuamos con el análisis iniciado en los Ejercicios 1.7, 2.22, 3.6 y 4.7. El enfoque de este ejercicio es la selección de variables.

Comienza con los datos de $n=185$ países de todo el mundo que tienen expectativas de vida válidas (no faltantes). Grafica la expectativa de vida frente al producto interno bruto y los gastos privados en salud. A partir de estos gráficos, describe por qué es deseable utilizar transformaciones logarítmicas, lnGDP y lnHEALTH, respectivamente. También grafica la expectativa de vida frente a lnGDP y lnHEALTH para confirmar tu intuición.
Utiliza un algoritmo de regresión paso a paso para ayudarte a seleccionar un modelo. No consideres las variables RESEARCHERS, SMOKING y FEMALEBOSS ya que tienen muchos valores faltantes. Para las variables restantes, utiliza solo las observaciones sin valores faltantes. Hazlo dos veces, con y sin la variable categórica REGION.
Regresa al conjunto de datos completo de $n=185$ países y ejecuta un modelo de regresión usando FERTILITY, PUBLICEDUCATION y lnHEALTH como variables explicativas.

c(i). Proporciona histogramas de residuos estandarizados y apalancamientos.
c(ii). Identifica el residuo estandarizado y el apalancamiento asociados con Lesoto, anteriormente Basutolandia, un reino rodeado por Sudáfrica. ¿Es esta observación un valor atípico, un punto de alto apalancamiento, o ambos?
c(iii). Repite la regresión sin Lesoto. Cita cualquier diferencia en los coeficientes estadísticos entre este modelo y el del apartado c(i).

5.4. Seguro de Vida a Término. Continuamos con nuestro estudio de la Demanda de Seguro de Vida a Término de los Capítulos 3 y 4. Específicamente, examinamos la Encuesta de Finanzas del Consumidor (SCF) de 2004, una muestra representativa a nivel nacional que contiene información extensa sobre activos, pasivos, ingresos y características demográficas de los encuestados (potenciales clientes de EE.UU.). Estudiamos una muestra aleatoria de 500 familias con ingresos positivos. De la muestra de 500, inicialmente consideramos una submuestra de $n=275$ familias que compraron seguro de vida a término.

Considera una regresión lineal de LNINCOME, EDUCATION, NUMHH, MARSTAT, AGE y GENDER sobre LNFACE.

Colinealidad. No todas las variables resultaron ser estadísticamente significativas. Para investigar una posible explicación, calcula los factores de inflación de la varianza.

a(i). Explica brevemente la idea de colinealidad y un factor de inflación de la varianza.
a(ii). ¿Qué constituye un gran factor de inflación de la varianza?
a(iii). Si se detecta un gran factor de inflación de la varianza, ¿qué posibles acciones podemos tomar para abordar este aspecto de los datos?
a(iv). Complementa las estadísticas de los factores de inflación de la varianza con una tabla de correlaciones de las variables explicativas. Basado en estas estadísticas, ¿es la colinealidad un problema con este modelo ajustado? ¿Por qué o por qué no?
Puntos Inusuales. A veces, un ajuste deficiente del modelo puede deberse a puntos inusuales.

b(i). Define la idea de apalancamiento para una observación.
b(ii). Para este modelo ajustado, da reglas generales para identificar puntos con apalancamiento inusual. Identifica cualquier punto inusual.
b(iii). Un analista está preocupado por los valores de apalancamiento de este modelo ajustado y sugiere usar FACE como la variable dependiente en lugar de LNFACE. Describe cómo cambiarían los valores de apalancamiento usando esta variable dependiente alternativa.
Análisis de Residuos. Podemos aprender cómo mejorar los ajustes del modelo a partir de los análisis de residuos.

c(i). Proporciona un gráfico de residuos frente a valores ajustados. ¿Qué esperamos aprender de este tipo de gráfico? ¿Este gráfico muestra alguna inadecuación del modelo?
c(ii). Proporciona un gráfico $qq$ de residuos. ¿Qué esperamos aprender de este tipo de gráfico? ¿Este gráfico muestra alguna inadecuación del modelo?
c(iii). Proporciona un gráfico de residuos frente a apalancamientos. ¿Qué esperamos aprender de este tipo de gráfico? ¿Este gráfico muestra alguna inadecuación del modelo?
Regresión Paso a Paso. Ejecuta un algoritmo de regresión paso a paso. Supón que este algoritmo sugiere un modelo utilizando LNINCOME, EDUCATION, NUMHH y GENDER como variables explicativas para predecir la variable dependiente LNFACE.

d(i). ¿Cuál es el propósito de la regresión paso a paso?
d(ii). Describe dos desventajas importantes de los algoritmos de regresión paso a paso.

5.10 Suplementos Técnicos para el Capítulo 5

5.10.1 Matriz de Proyección

Matriz de Sombrero. Definimos la matriz de sombrero como $\mathbf{H} = \mathbf{X(X}^{\prime}\mathbf{X)}^{-1} \mathbf{X}^{\prime}$, de manera que $\mathbf{\hat{y}} = \mathbf{X b} = \mathbf{Hy}$. De esto, se dice que la matriz $\mathbf{H}$ proyecta el vector de respuestas $\mathbf{y}$ sobre el vector de valores ajustados $\mathbf{\hat{y}}$.

Dado que $\mathbf{H}^{\prime} = \mathbf{H}$, la matriz de sombrero es simétrica. Además, también es una matriz idempotente debido a la propiedad de que $\mathbf{HH} = \mathbf{H}$. Para ver esto, tenemos que \[ \begin{array}{ll} \mathbf{HH} &= \mathbf{(X(\mathbf{X}^{\prime}X)}^{-1}\mathbf{X}^{\prime}\mathbf{)(X(\mathbf{X}^{\prime}X)}^{-1}\mathbf{X}^{\prime}\mathbf{)} \\ &= \mathbf{X(\mathbf{X}^{\prime}X)}^{-1}\mathbf{(\mathbf{X}^{\prime}X)(\mathbf{X}^{\prime}X)}^{-1}\mathbf{X}^{\prime} = \mathbf{X(\mathbf{X}^{\prime}X)}^{-1}\mathbf{X}^{\prime} = \mathbf{H}. \end{array} \] De manera similar, es fácil verificar que $\mathbf{I-H}$ es idempotente. Dado que $\mathbf{H}$ es idempotente, a partir de algunos resultados en álgebra de matrices, es sencillo mostrar que \[ \sum_{i=1}^{n} h_{ii} = k + 1. \] Como se discutió en la Sección 5.4.1, usamos nuestros límites y el apalancamiento promedio, $\bar{h} = (k + 1)/n$, para ayudar a identificar observaciones con apalancamiento inusualmente alto.

Varianza de los Residuos. Usando la ecuación del modelo $\mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}$, podemos expresar el vector de residuos como \[\begin{equation} \mathbf{e} = \mathbf{y} - \mathbf{\hat{y}} = \mathbf{y - Hy} = \mathbf{(I-H)(X \boldsymbol{\beta} + \boldsymbol{\varepsilon})} = \mathbf{(I-H) \boldsymbol{\varepsilon}}. \tag{5.14} \end{equation}\] La última igualdad se debe al hecho de que $\mathbf{(I-H)X} = \mathbf{X - HX} = \mathbf{X - X} = \mathbf{0}$. Usando $\text{Var~} \boldsymbol{\varepsilon} = \sigma^2 \mathbf{I}$, tenemos \[ \begin{array}{ll} \text{Var } \mathbf{e} &= \text{Var }\left[ \mathbf{(I-H)\boldsymbol{\varepsilon}} \right] = \mathbf{(I-H)} \text{Var } \boldsymbol{\varepsilon} \mathbf{(I-H)} \\ &= \sigma^2 \mathbf{(I-H)} \mathbf{I} \mathbf{(I-H)} = \sigma^2 \mathbf{(I-H)}. \end{array} \] La última igualdad proviene del hecho de que $\mathbf{I-H}$ es idempotente. Así, tenemos que \[\begin{equation} \text{Var } e_i = \sigma^2 (1 - h_{ii}) \text{ y Cov } (e_i, e_j) = -\sigma^2 h_{ij}. \tag{5.15} \end{equation}\] Así, aunque los errores verdaderos $\boldsymbol{\varepsilon}$ son no correlacionados, hay una pequeña correlación negativa entre los residuos $\mathbf{e}$.

Dominio del Error en el Residuo. Examinando la fila $i$-ésima de la ecuación (5.14), tenemos que el residuo $i$-ésimo \[\begin{equation} e_i = \varepsilon_i - \sum_{j=1}^{n} h_{ij} \varepsilon_j \tag{5.16} \end{equation}\] se puede expresar como una combinación lineal de errores independientes. La relación $\mathbf{H} = \mathbf{HH}$ da lugar a \[\begin{equation} h_{ii} = \sum_{j=1}^{n} h_{ij}^2. \tag{5.17} \end{equation}\] Dado que $h_{ii}$ es, en promedio, $(k + 1)/n$, esto indica que cada $h_{ij}$ es pequeño en relación con 1. Así, al interpretar la ecuación (5.16), decimos que la mayor parte de la información en $e_i$ se debe a $\varepsilon_i$.

Correlaciones con los Residuos. Primero define $\mathbf{x}^j = (x_{1j}, x_{2j}, \dots, x_{nj})^{\prime}$ como la columna que representa la $j$-ésima variable. Con esta notación, podemos particionar la matriz de variables explicativas como $\mathbf{X} = \left( \mathbf{x}^{0}, \mathbf{x}^{1}, \dots, \mathbf{x}^{k} \right)$. Ahora, examinando la columna $j$-ésima de la relación $\mathbf{(I-H)X} = \mathbf{0}$, tenemos $\mathbf{(I-H)x}^{j} = \mathbf{0}$. Con $\mathbf{e} = \mathbf{(I-H) \boldsymbol{\varepsilon}}$, esto da \[ \mathbf{e}^{\prime} \mathbf{x}^{j} = \boldsymbol{\varepsilon}^{\prime} \mathbf{(I-H)x}^{j} = 0, \] para $j = 0, 1, \ldots, k.$ Este resultado tiene varias implicaciones. Si el intercepto está en el modelo, entonces $\mathbf{x}^{0} = (1, 1, \ldots, 1)^{\prime}$ es un vector de unos. Aquí, $\mathbf{e}^{\prime} \mathbf{x}^{0} = 0$ significa que $\sum_{i=1}^{n} e_i = 0$ o, el residuo promedio es cero. Además, dado que $\mathbf{e}^{\prime} \mathbf{x}^{j} = 0$, es fácil verificar que la correlación muestral entre $\mathbf{e}$ y $\mathbf{x}^{j}$ es cero. En la misma línea, también tenemos que $\mathbf{e}^{\prime} \mathbf{\hat{y}} = \mathbf{e}^{\prime} \mathbf{(I-H)Xb} = \mathbf{0}$. Así, usando el mismo argumento que antes, la correlación muestral entre $\mathbf{e}$ y $\mathbf{\hat{y}}$ es cero.

Coeficiente de Correlación Múltiple. Para un ejemplo de una correlación diferente de cero, considera $r(\mathbf{y, \hat{y}})$, la correlación muestral entre $\mathbf{y}$ y $\mathbf{\hat{y}}$. Dado que $\mathbf{(I-H)x}^{0} = \mathbf{0}$, tenemos $\mathbf{x}^{0} = \mathbf{Hx}^{0}$ y, por lo tanto, $\mathbf{\hat{y}}^{\prime} \mathbf{x}^{0} = \mathbf{y}^{\prime} \mathbf{Hx}^{0} = \mathbf{y^{\prime} x}^{0}$. Asumiendo que $\mathbf{x}^{0} = (1, 1, \ldots, 1)^{\prime}$, esto significa que $\sum_{i=1}^{n} \hat{y}_i = \sum_{i=1}^{n} y_i$, por lo que el valor promedio ajustado es $\bar{y}$.

\[ r(\mathbf{y, \hat{y}}) = \frac{\sum_{i=1}^{n} (y_i - \bar{y})(\hat{y}_i - \bar{y})}{(n-1) s_y s_{\hat{y}}}. \]

Recuerda que $(n-1) s_y^2 = \sum_{i=1}^{n} (y_i - \bar{y})^2 = Total ~SS$ y $(n-1) s_{\hat{y}}^2 = \sum_{i=1}^{n} (\hat{y}_i - \bar{y})^2 = Regress ~SS$. Además, con $\mathbf{x}^0 = (1, 1, \ldots, 1)^{\prime}$, \[ \begin{array}{ll} \sum_{i=1}^{n} (y_i - \bar{y})(\hat{y}_i - \bar{y}) &= (\mathbf{y} - \bar{y} \mathbf{x}^0)^{\prime} (\mathbf{\hat{y}} - \bar{y} \mathbf{x}^0) = \mathbf{y}^{\prime} \mathbf{\hat{y}} - \bar{y}^2 \mathbf{x}^{0 \prime} \mathbf{x}^0 \\ &= \mathbf{y}^{\prime} \mathbf{Xb} - n \bar{y}^2 = Regress ~SS. \end{array} \]

Esto da \[\begin{equation} r(\mathbf{y, \hat{y}}) = \frac{Regress ~SS}{\sqrt{\left( Total ~SS \right) \left( Regress ~SS \right)}} = \sqrt{\frac{Regress ~SS}{Total ~SS}} = \sqrt{R^2}. \tag{5.18} \end{equation}\] Es decir, el coeficiente de determinación se puede interpretar como la raíz cuadrada de la correlación entre las respuestas observadas y las ajustadas.

5.10.2 Estadísticas Leave-One-Out

Notación. Para probar la sensibilidad de las cantidades de regresión, hay varias estadísticas de interés que se basan en la noción de “dejar fuera” u omitir una observación. Con este fin, la notación de subíndice $(i)$ significa dejar fuera la $i$-ésima observación. Por ejemplo, omitir la fila de variables explicativas $\mathbf{x}_i^{\prime} = (x_{i0}, x_{i1}, \dots, x_{ik})$ de $\mathbf{X}$ da lugar a $\mathbf{X}_{(i)}$, una matriz de $(n-1) \times (k+1)$ de variables explicativas. De manera similar, $\mathbf{y}_{(i)}$ es un vector de $(n-1) \times 1$, basado en eliminar la $i$-ésima fila de $\mathbf{y}$.

Resultado Básico de Matrices. Supongamos que $\mathbf{A}$ es una matriz invertible de $p \times p$ y $\mathbf{z}$ es un vector de $p \times 1$. El siguiente resultado de álgebra de matrices proporciona una herramienta importante para entender las estadísticas leave-one-out en el análisis de regresión lineal. \[\begin{equation} \left( \mathbf{A - zz}^{\prime} \right)^{-1} = \mathbf{A}^{-1} + \frac{\mathbf{A}^{-1} \mathbf{zz}^{\prime} \mathbf{A}^{-1}}{1 - \mathbf{z}^{\prime} \mathbf{A}^{-1} \mathbf{z}}. \tag{5.19} \end{equation}\] Para verificar este resultado, simplemente multiplica $\mathbf{A - zz}^{\prime}$ por el lado derecho de la ecuación para obtener $\mathbf{I}$, la matriz identidad.

Vector de Coeficientes de Regresión. Al omitir la $i$-ésima observación, nuestro nuevo vector de coeficientes de regresión es $\mathbf{b}_{(i)} = \left( \mathbf{X}_{(i)}^{\prime} \mathbf{X}_{(i)} \right)^{-1} \mathbf{X}_{(i)}^{\prime} \mathbf{y}_{(i)}.$ Una expresión alternativa para $\mathbf{b}_{(i)}$ que resulta ser más simple de calcular es \[\begin{equation} \mathbf{b}_{(i)} = \mathbf{b} - \frac{\left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i e_i}{1 - h_{ii}}. \tag{5.20} \end{equation}\] Para verificar esto, primero usa el resultado de inversión de matrices con $\mathbf{A} = \mathbf{X}^{\prime} \mathbf{X}$ y $\mathbf{z} = \mathbf{x}_i$ para obtener \[ \left( \mathbf{X}_{(i)}^{\prime} \mathbf{X}_{(i)} \right)^{-1} = (\mathbf{X}^{\prime} \mathbf{X} - \mathbf{x}_i \mathbf{x}_i^{\prime})^{-1} = (\mathbf{X}^{\prime} \mathbf{X})^{-1} + \frac{\left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i \mathbf{x}_i^{\prime} \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1}}{1 - h_{ii}}, \] donde, a partir del resultado de apalancamiento, tenemos $h_{ii} = \mathbf{x}_i^{\prime} (\mathbf{X}^{\prime} \mathbf{X})^{-1} \mathbf{x}_i$. Multiplicando cada lado por \[ \mathbf{X}_{(i)}^{\prime} \mathbf{y}_{(i)} = \mathbf{X}^{\prime} \mathbf{y} - \mathbf{x}_i y_i \] da $$ \[\begin{array}{ll} \mathbf{b}_{(i)} &= \left( \mathbf{X}_{(i)}^{\prime} \mathbf{X}_{(i)} \right)^{-1} \mathbf{X}_{(i)}^{\prime} \mathbf{y}_{(i)} \\ &= \left( (\mathbf{X}^{\prime} \mathbf{X})^{-1} + \frac{\left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i \mathbf{x}_i^{\prime} \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1}}{1 - h_{ii}} \right) \left( \mathbf{X}^{\prime} \mathbf{y} - \mathbf{x}_i y_i \right) \\ &= \mathbf{b} - \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i y_i + \frac{\left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i \mathbf{x}_i^{\prime} \mathbf{b} - \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i \mathbf{x}_i^{\prime} \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i y_i}{1 - h_{ii}} \\ &= \mathbf{b} - \frac{\left( 1 - h_{ii} \right) \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i y_i - \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i \mathbf{x}_i^{\prime} \mathbf{b} - \left( \mathbf{ X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i h_{ii} y_i}{1 - h_{ii}} \\ &= \mathbf{b} - \frac{\left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i y_i - \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i \mathbf{x}_i^{\prime} \mathbf{b}}{1 - h_{ii}} \\ &= \mathbf{b} - \frac{\left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i e_i}{1 - h_{ii}}. \end{array}\]

$$ Esto establece el resultado.

Distancia de Cook. Para medir el efecto, o influencia, de omitir la $i$-ésima observación, Cook examinó la diferencia entre los valores ajustados con y sin la observación. Definimos la Distancia de Cook como \[ D_i = \frac{\left( \mathbf{\hat{y} - \hat{y}}_{(i)} \right)^{\prime} \left( \mathbf{\hat{y} - \hat{y}}_{(i)} \right)}{(k+1) s^2} \] donde $\mathbf{\hat{y}}_{(i)} = \mathbf{Xb}_{(i)}$ es el vector de valores ajustados calculado omitiendo el punto $i$-ésimo. Usando la ecuación (5.20) y $\mathbf{\hat{y}} = \mathbf{Xb}$, una expresión alternativa para la Distancia de Cook es \[ \begin{array}{ll} D_i &= \frac{\left( \mathbf{b - b}_{(i)} \right)^{\prime} \left( \mathbf{X}^{\prime} \mathbf{X} \right) \left( \mathbf{b - b}_{(i)} \right)}{(k+1) s^2} \\ &= \frac{e_i^2}{(1 - h_{ii})^2} \frac{\mathbf{x}_i^{\prime} \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \left( \mathbf{X}^{\prime} \mathbf{X} \right) \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i}{(k+1) s^2} \\ & = \frac{e_i^2}{(1 - h_{ii})^2} \frac{h_{ii}}{(k+1) s^2} \\ &= \left( \frac{e_i}{s \sqrt{1 - h_{ii}}} \right)^2 \frac{h_{ii}}{(k+1) (1 - h_{ii})}. \end{array} \] Este resultado no solo es útil computacionalmente, sino que también sirve para descomponer la estadística en la parte debida al residuo estandarizado, $(e_i/(s \sqrt{1 - h_{ii}}))^2$, y en la parte debida al apalancamiento, $\frac{h_{ii}}{(k+1) (1 - h_{ii})}$.

Residuo Leave-One-Out. El residuo leave-one-out se define como $e_{(i)} = y_i - \mathbf{x}_i^{\prime} \mathbf{b}_{(i)}$. Se usa en el cálculo de la estadística PRESS, descrita en la Sección 5.6.3. Una expresión computacional simple es $e_{(i)} = \frac{e_i}{1 - h_{ii}}$. Para verificar esto, usa la ecuación (5.20) para obtener \[ e_{(i)} = y_i - \mathbf{x}_i^{\prime} \mathbf{b}_{(i)} = y_i - \mathbf{x}_i^{\prime} \left( \mathbf{b} - \frac{\left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i e_i}{1 - h_{ii}} \right) \] \[ = e_i + \frac{\mathbf{x}_i \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i e_i}{1 - h_{ii}} = e_i + \frac{h_{ii} e_i}{1 - h_{ii}} = \frac{e_i}{1 - h_{ii}}. \]

Estimación de Varianza Leave-One-Out. La estimación leave-one-out de la varianza se define como \[ s_{(i)}^2 = \frac{((n - 1) - (k + 1))^{-1} \sum_{j \ne i} \left( y_j - \mathbf{x}_j^{\prime} \mathbf{b}_{(i)} \right)^2}{(n - 1) - (k + 1)}. \] Se usa en la definición del residuo estandarizado, definido en la Sección 5.3.1. Una expresión computacional simple está dada por \[\begin{equation} s_{(i)}^2 = \frac{(n - (k + 1)) s^2 - \frac{e_i^2}{1 - h_{ii}}}{(n - 1) - (k + 1)}. \tag{5.21} \end{equation}\] Para ver esto, primero nota que, a partir de la ecuación (5.14), tenemos $\mathbf{He} = \mathbf{H(I - H) \boldsymbol{\varepsilon}} = \mathbf{0}$, porque $\mathbf{H} = \mathbf{HH}$. En particular, desde la fila $i$-ésima de $\mathbf{He} = \mathbf{0}$, tenemos $\sum_{j=1}^{n} h_{ij} e_j = 0$. Ahora, usando las ecuaciones (5.17) y (5.20), tenemos \[ \begin{array}{ll} \sum_{j \ne i} \left( y_j - \mathbf{x}_j^{\prime} \mathbf{b}_{(i)} \right)^2 &= \sum_{j=1}^{n} \left( y_j - \mathbf{x}_j^{\prime} \mathbf{b}_{(i)} \right)^2 - \left( y_i - \mathbf{x}_i^{\prime} \mathbf{b}_{(i)} \right)^2 \\ &= \sum_{j=1}^{n} \left( y_j - \mathbf{x}_j^{\prime} \mathbf{b} + \frac{\mathbf{x}_j^{\prime} \left( \mathbf{X}^{\prime} \mathbf{X} \right)^{-1} \mathbf{x}_i e_i}{1 - h_{ii}} \right) - e_{(i)}^2 \\ &= \sum_{j=1}^{n} \left( e_j + \frac{h_{ij} e_i}{1 - h_{ii}} \right)^2 - \frac{e_i^2}{(1 - h_{ii})^2} \\ &= \sum_{j=1}^{n} e_j^2 + 0 + \frac{e_i^2}{(1 - h_{ii})^2} h_{ii} - \frac{e_i^2}{(1 - h_{ii})^2} \\ &= \sum_{j=1}^{n} e_j^2 - \frac{e_i^2}{1 - h_{ii}} = (n - (k + 1)) s^2 - \frac{e_i^2}{1 - h_{ii}}. \end{array} \]

Esto establece la ecuación (5.21).

5.10.3 Omisión de Variables

Notación. Para medir el efecto en las cantidades de regresión, hay una serie de estadísticas de interés basadas en la noción de omitir una variable explicativa. A tal fin, la notación de superíndice $(j)$ significa omitir la $j$-ésima variable, donde $j=0,1,\ldots,k$. Primero, recuerda que $\mathbf{x}^{j} = (x_{1j}, x_{2j}, \ldots, x_{nj})^{\prime}$ es la columna que representa la $j$-ésima variable. Además, define $\mathbf{X}^{(j)}$ como la matriz $n \times k$ de variables explicativas definida al eliminar $\mathbf{x}^{j}$ de $\mathbf{X}$. Por ejemplo, tomando $j=k$, a menudo particionamos $\mathbf{X}$ como $\mathbf{X} = \left( \mathbf{X}^{(k)}: \mathbf{x}^k \right)$. Usando los resultados de la Sección 4.7.2, utilizaremos $\mathbf{X}^{(k)} = \mathbf{X}_1$ y $\mathbf{x}^k = \mathbf{X}_2$.

Factor de Inflación de la Varianza. Primero, nos gustaría establecer la relación entre la definición del error estándar de $b_j$ dada por \[ se(b_j) = s \sqrt{(j+1)\text{ésimo elemento diagonal de }(\mathbf{X}^{\prime}\mathbf{X})^{-1}} \] y la relación que involucra el factor de inflación de la varianza, \[ se(b_j) = s \frac{\sqrt{VIF_j}}{s_{x_j}\sqrt{n-1}}. \] Por simetría de las variables independientes, solo necesitamos considerar el caso donde $j=k$. Así, nos gustaría establecer \[\begin{equation} (k+1)\text{ésimo elemento diagonal de }(\mathbf{X}^{\prime}\mathbf{X})^{-1} = \frac{VIF_{k}}{(n-1) s_{x_{k}}^2}. \tag{5.22} \end{equation}\] Primero considera el modelo reparametrizado en la ecuación (4.22). A partir de la ecuación (4.23), podemos expresar la estimación del coeficiente de regresión \[ b_{k} = \frac{\mathbf{e}_1^{\prime}\mathbf{y}}{\mathbf{e}_1^{\prime}\mathbf{e}_1}. \] De la ecuación (4.23), tenemos que $\text{Var} \, b_{k} = \sigma^2 (\mathbf{E}_2^{\prime} \mathbf{E}_2)^{-1}$ y así \[\begin{equation} se(b_{k}) = s (\mathbf{E}_2^{\prime} \mathbf{E}_2)^{-1/2}. \tag{5.23} \end{equation}\] Así, $(\mathbf{E}_2^{\prime} \mathbf{E}_2)^{-1}$ es el $(k+1)$-ésimo elemento diagonal de \[ \left( \begin{bmatrix} \mathbf{X}_1^{\prime} \\ \mathbf{E}_2^{\prime} \end{bmatrix} \begin{bmatrix} \mathbf{X}_1 & \mathbf{E}_2 \end{bmatrix} \right)^{-1} \] y también es el $(k+1)$-ésimo elemento diagonal de $(\mathbf{X}^{\prime} \mathbf{X})^{-1}$. Alternativamente, esto se puede verificar directamente utilizando la inversa de la matriz particionada en la ecuación (4.19).

Ahora, supongamos que realizamos una regresión usando $\mathbf{x}^{k} = \mathbf{X}_2$ como el vector de respuesta y $\mathbf{X}^{(k)} = \mathbf{X}_1$ como la matriz de variables explicativas. Como se anotó arriba en la ecuación (4.22), $\mathbf{E}_2$ representa los “residuos” de esta regresión y así $\mathbf{E}_2^{\prime} \mathbf{E}_2$ representa la suma de cuadrados del error. Para esta regresión, la suma total de cuadrados es \[ \sum_{i=1}^{n} (x_{ik} - \bar{x}_{k})^2 = (n-1) s_{x_{k}}^2 \] y el coeficiente de determinación es $R_{k}^2$. Así, \[ \mathbf{E}_2^{\prime} \mathbf{E}_2 = Error ~SS = Total ~SS (1 - R_{k}^2) = \frac{(n-1) s_{x_{k}}^2}{VIF_{k}}. \] Esto establece el resultado.

Estableciendo $t^2 = F$. Para probar la hipótesis nula $H_0$: $\beta_{k} = 0$, el material en la Sección 3.4.1 proporciona una descripción de una prueba basada en el estadístico $t$, $t(b_{k}) = \frac{b_{k}}{se(b_{k})}$. Un procedimiento alternativo de prueba, descrito en las Secciones 4.2.2, utiliza el estadístico de prueba \[ F-\text{ratio} = \frac{(Error ~SS)_{reducido} - (Error ~SS)_{completo}}{p \times (Error~MS)_{completo}} = \frac{\left( \mathbf{E}_2^{\prime} \mathbf{y} \right)^2}{s^2 \mathbf{E}_2^{\prime} \mathbf{E}_2} \] de la ecuación (4.26). Alternativamente, a partir de las ecuaciones (4.23) y (5.23), tenemos \[\begin{equation} t(b_{k}) = \frac{b_{k}}{se(b_{k})} = \frac{\left( \mathbf{E}_2^{\prime} \mathbf{y} \right) / \left( \mathbf{E}_2^{\prime} \mathbf{E}_2 \right)}{s / \sqrt{\mathbf{E}_2^{\prime} \mathbf{E}_2}} = \frac{\left( \mathbf{E}_2^{\prime} \mathbf{y} \right)}{s \sqrt{\mathbf{E}_2^{\prime} \mathbf{E}_2}}. \tag{5.24} \end{equation}\]

Así, $t(b_{k})^2 = F$-ratio.

Coeficientes de Correlación Parcial. A partir del modelo de regresión completo \[ \mathbf{y} = \mathbf{X}^{(k)} \boldsymbol{\beta}^{(k)} + \mathbf{x}_{k} \beta_{k} + \boldsymbol{\varepsilon}, \] considera dos regresiones separadas. Una regresión usando $\mathbf{x}^{k}$ como el vector de respuesta y $\mathbf{X}^{(k)}$ como la matriz de variables explicativas produce los residuos $\mathbf{E}_2$. De manera similar, una regresión con $\mathbf{y}$ como el vector de respuesta y $\mathbf{X}^{(k)}$ como la matriz de variables explicativas produce los residuos \[ \mathbf{E}_1 = \mathbf{y} - \mathbf{X}^{(k)} \left( \mathbf{X}^{(k)\prime} \mathbf{X}^{(k)} \right)^{-1} \mathbf{X}^{(k)} \mathbf{y}. \] Si $x^{0} = (1,1,\ldots,1)^{\prime}$, entonces el promedio de $\mathbf{E}_1$ y $\mathbf{E}_2$ es cero. En este caso, la correlación muestral entre $\mathbf{E}_1$ y $\mathbf{E}_2$ es \[ r(\mathbf{E}_1, \mathbf{E}_2) = \frac{\sum_{i=1}^{n} E_{1i} E_{2i}}{\sqrt{\left( \sum_{i=1}^{n} E_{1i}^2 \right) \left( \sum_{i=1}^{n} E_{2i}^2 \right)}} = \frac{\mathbf{E}_1^{\prime} \mathbf{E}_2}{\sqrt{\left( \mathbf{E}_1^{\prime} \mathbf{E}_1 \right) \left( \mathbf{E}_2^{\prime} \mathbf{E}_2 \right)}}. \] Como $\mathbf{E}_2$ es un vector de residuos usando $\mathbf{X}^{(k)}$ como la matriz de variables explicativas, tenemos que $\mathbf{E}_2^{\prime} \mathbf{X}^{(k)} = 0$. Así, para el numerador, tenemos \[ \mathbf{E}_2^{\prime} \mathbf{E}_1 = \mathbf{E}_2^{\prime} \left( \mathbf{y} - \mathbf{X}^{(k)} \left( \mathbf{X}^{(k)\prime} \mathbf{X}^{(k)} \right)^{-1} \mathbf{X}^{(k)} \mathbf{y} \right) = \mathbf{E}_2^{\prime} \mathbf{y}. \] A partir de las ecuaciones (4.24) y (4.25), tenemos que \[ (n - (k+1)) s^2 = (Error ~SS)_{completo} = \mathbf{E}_1^{\prime} \mathbf{E}_1 - \frac{\left( \mathbf{E}_1^{\prime} \mathbf{y} \right)^2}{\mathbf{E}_2^{\prime} \mathbf{E}_2} = \mathbf{E}_1^{\prime} \mathbf{E}_1 - \frac{\left( \mathbf{E}_1^{\prime} \mathbf{E}_2 \right)^2}{\mathbf{E}_2^{\prime} \mathbf{E}_2}. \] Así, a partir de la ecuación (5.24) \[ \begin{array}{ll} \frac{t(b_{k})}{\sqrt{t(b_{k})^2 + n - (k+1)}} &= \frac{\mathbf{E}_2^{\prime} \mathbf{y} / \left(s \sqrt{\mathbf{E}_2^{\prime} \mathbf{E}_2}\right)}{\sqrt{\frac{\left( \mathbf{E}_2^{\prime} \mathbf{y} \right)^2}{s^2 \mathbf{E}_2^{\prime} \mathbf{E}_2} + n - (k+1)}} \\ & = \frac{\mathbf{E}_2^{\prime} \mathbf{y}}{\sqrt{\left( \mathbf{E}_2^{\prime} \mathbf{y} \right)^2 + \mathbf{E}_2^{\prime} \mathbf{E}_2 s^2 \left(n - (k+1) \right)}} \\ & = \frac{\mathbf{E}_2^{\prime} \mathbf{E}_1}{\sqrt{\left( \mathbf{E}_2^{\prime} \mathbf{E}_1 \right)^2 + \mathbf{E}_2^{\prime} \mathbf{E}_2 \left( \mathbf{E}_1^{\prime} \mathbf{E}_1 - \frac{\left( \mathbf{E}_2^{\prime} \mathbf{E}_1 \right)^2}{\mathbf{E}_2^{\prime} \mathbf{E}_2} \right)}} \\ &= \frac{\mathbf{E}_1^{\prime} \mathbf{E}_2}{\sqrt{(\mathbf{E}_1^{\prime} \mathbf{E}_1) (\mathbf{E}_2^{\prime} \mathbf{E}_2)}} = r(\mathbf{E}_1, \mathbf{E}_2). \end{array} \] Esto establece la relación entre el coeficiente de correlación parcial y el estadístico $t$-ratio.

	\(x_1\)	\(x_2\)
\(x_2\)	0.972
\(y\)	0.188	-0.022

Expression	Combinations	Models
E \(y=\beta_0\)		1 modelo sin variables independientes
E \(y=\beta_0+\beta_1x_i\)	\(i\) = 1,2,3,4	4 modelos con una variable independiente
E \(y = \beta_0 + \beta_1 x_i + \beta_2 x_j\)	(\(i,j\)) = (1,2),(1,3),(1,4),(2,3),(2,4),(3,4)	6 modelos con dos variables independientes
E \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_j +\beta_3x_{k}\)	(\(i,j,k\)) = (1,2,3),(1,2,4),(1,3,4),(2,3,4)	4 modelos con tres variables independientes
E \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 +\beta_3 x_3 + \beta_4 x_4\)		1 modelo con todas las variables independientes