Capítulo 7 Modelado de Tendencias

Vista previa del capítulo. Este capítulo inicia nuestro estudio de los datos de series temporales introduciendo técnicas para identificar patrones principales, o tendencias, en datos que evolucionan con el tiempo. El enfoque está en cómo las técnicas de regresión desarrolladas en capítulos anteriores pueden ser utilizadas para modelar tendencias. Además, se presentan nuevas técnicas, como la diferenciación de datos, que nos permiten introducir de forma natural un paseo aleatorio, un modelo importante de mercados financieros eficientes.

7.1 Introducción

Series Temporales y Procesos Estocásticos

Las empresas no se definen por estructuras físicas como los sólidos edificios de piedra que simbolizan la seguridad financiera. Tampoco se definen por los juguetes de invasores espaciales que fabrican para niños. Las empresas están compuestas por varios procesos complejos e interrelacionados. Un proceso es una serie de acciones u operaciones que conducen a un resultado particular.

Los procesos no solo son los elementos fundamentales de las empresas, sino que también forman la base de nuestras vidas cotidianas. Podemos ir al trabajo o a la escuela todos los días, practicar artes marciales o estudiar estadística. Estas son secuencias regulares de actividades que nos definen. En este texto, nos interesa modelar procesos estocásticos, definidos como colecciones ordenadas de variables aleatorias, que cuantifican un proceso de interés.

Algunos procesos evolucionan con el tiempo, como los viajes diarios al trabajo o a la escuela y los ingresos trimestrales de una empresa. Usamos el término datos longitudinales para referirnos a las mediciones de un proceso que evoluciona en el tiempo. Una única medición de un proceso genera una variable en el tiempo, denotada como \(y_1, ..., y_T,\) y conocida como una serie temporal.
En esta parte del texto, seguimos la práctica común y usamos \(T\) para denotar el número de observaciones disponibles (en lugar de \(n\)). El Capítulo 10 describirá otro tipo de datos longitudinales donde examinamos una sección transversal de entidades, como empresas, y observamos su evolución a lo largo del tiempo. Este tipo de datos también se conoce como datos de panel.

Las colecciones de variables aleatorias pueden estar ordenadas de formas distintas al tiempo. Por ejemplo, los daños por huracanes se registran en el lugar donde ocurrieron y, por lo tanto, están ordenados espacialmente. Otro ejemplo es la evaluación de un proyecto de perforación petrolera, que requiere tomar muestras del suelo en varias longitudes, latitudes y profundidades. Esto genera observaciones ordenadas por las tres dimensiones del espacio, pero no por el tiempo. Un ejemplo adicional es el estudio de los agujeros en la capa de ozono, donde se toman mediciones atmosféricas. Como el interés radica en la tendencia del agotamiento del ozono, las mediciones se toman en varias longitudes, latitudes, alturas y momentos en el tiempo. Aunque solo consideramos procesos ordenados por tiempo, en otros estudios de datos longitudinales podrías encontrar ordenamientos alternativos. Los datos que no están ordenados se denominan datos de corte transversal.

Series Temporales versus Modelos Causales

Los métodos de regresión pueden ser utilizados para resumir muchos conjuntos de datos de series temporales. Sin embargo, usar técnicas de regresión sin establecer un contexto adecuado puede ser desastroso. Este concepto se refuerza con un ejemplo basado en el trabajo de Granger y Newbold (1974).

Ejemplo: Regresión Espuria. Sea \(\{\varepsilon_{x,t}\}\) y \(\{\varepsilon_{y,t}\}\) dos secuencias independientes, cada una de las cuales tiene una distribución normal estándar. A partir de estas, construimos recursivamente las variables \(x_t = 0.5 + x_{t-1} + \varepsilon_{x,t}\) y \(y_t = 0.5 + y_{t-1} + \varepsilon_{y,t}\), utilizando las condiciones iniciales \(x_0 = y_0 = 0\). (En la Sección 7.3, identificaremos \(x_t\) y \(y_t\) como modelos de paseo aleatorio). La Figura 7.1 muestra una realización de {\(x_t\)} y {\(y_t\)}, generada para \(T = 50\) observaciones usando simulación. El panel izquierdo muestra el crecimiento de cada serie en el tiempo: el aumento se debe a la adición de 0.5 en cada punto de tiempo. El panel derecho muestra una fuerte relación entre {\(x_t\)} y {\(y_t\)}: la correlación entre estas dos series resulta ser 0.92, a pesar de que las dos series fueron generadas independientemente. Su aparente relación, llamada espuria, se debe a que ambas están relacionadas con el crecimiento a lo largo del tiempo.

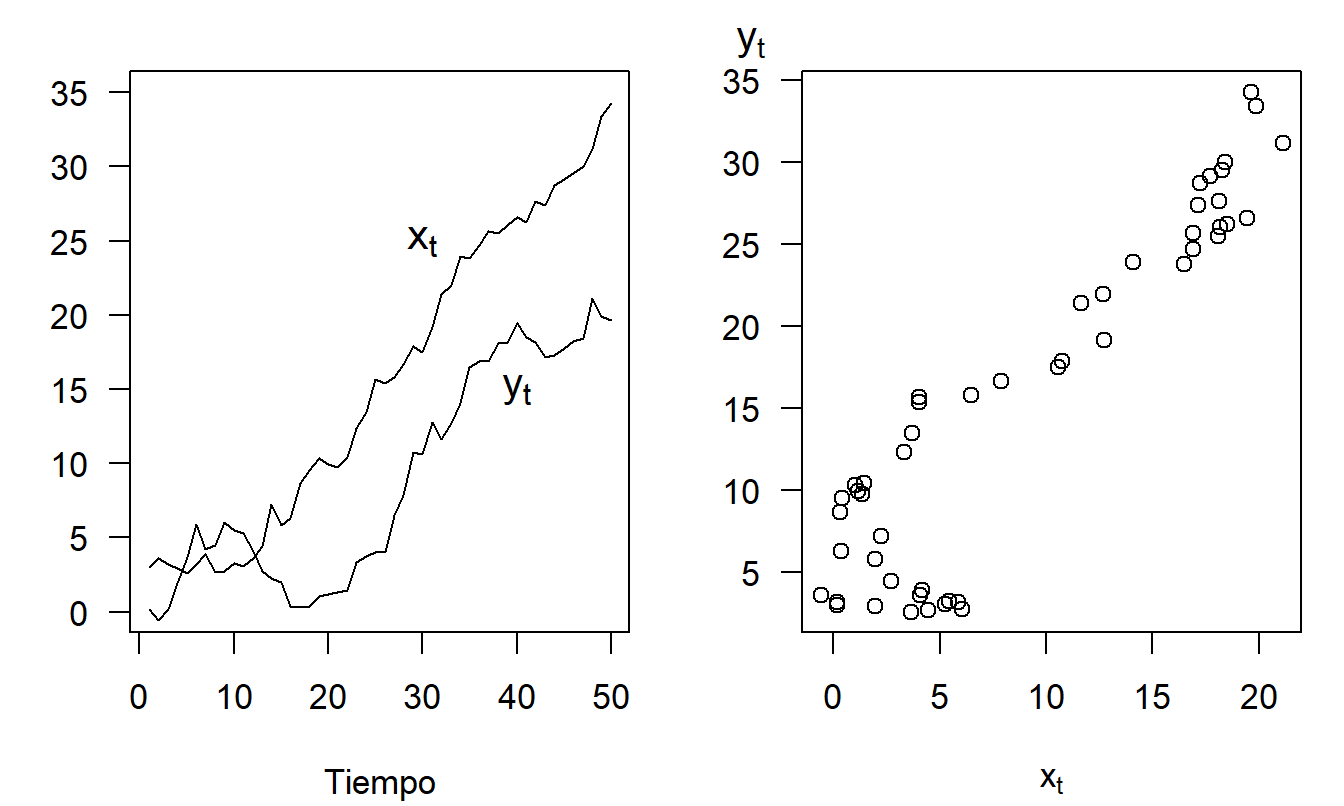
Regresiones Espurias. El panel izquierdo muestra dos series temporales que aumentan con el tiempo. El panel derecho muestra un diagrama de dispersión de las dos series, sugiriendo una relación positiva entre ellas. La relación es espuria en el sentido de que ambas series están impulsadas por el crecimiento en el tiempo, no por una dependencia positiva entre ellas.

Figura 7.1: Regresiones Espurias. El panel izquierdo muestra dos series temporales que aumentan con el tiempo. El panel derecho muestra un diagrama de dispersión de las dos series, sugiriendo una relación positiva entre ellas. La relación es espuria en el sentido de que ambas series están impulsadas por el crecimiento en el tiempo, no por una dependencia positiva entre ellas.

En un contexto longitudinal, los modelos de regresión de la forma \[ y_t = \beta_0 + \beta_1 x_t + \varepsilon_t \] se conocen como modelos causales. Los modelos causales se emplean regularmente en econometría, donde se supone que la teoría económica proporciona la información necesaria para especificar la relación causal (\(x\) “causa” \(y\)). En contraste, los modelos estadísticos solo pueden validar relaciones empíricas (“correlación, no causalidad”). En el ejemplo de regresión espuria, ambas variables evolucionan con el tiempo, por lo que un modelo que describa cómo una variable influye en otra necesita considerar los patrones temporales de las variables del lado izquierdo y derecho de la ecuación. Especificar modelos causales para aplicaciones actuariales puede ser difícil por esta razón: los patrones de series temporales en las variables explicativas pueden enmascarar o inducir una relación significativa con la variable dependiente. En contraste, el modelado de regresión puede aplicarse fácilmente cuando las variables explicativas son simplemente funciones del tiempo, el tema de la siguiente sección. Esto se debe a que las funciones del tiempo son determinísticas y, por lo tanto, no presentan patrones de series temporales.

Los modelos causales también tienen la desventaja de que sus aplicaciones están limitadas para fines de pronóstico. Esto se debe a que, para realizar un pronóstico de una realización futura de la serie, por ejemplo \(y_{T+2}\), se necesita tener conocimiento (o un buen pronóstico) de \(x_{T+2}\), el valor de la variable explicativa en el tiempo \(T+2\). Si \(x\) es una función conocida del tiempo (como en la siguiente sección), entonces esto no es un problema. Otra posibilidad es utilizar un valor rezagado de \(x\), como \(y_t = \beta_0 + \beta_1 x_{t-1} + \varepsilon_t\), de modo que los predictores a un paso sean posibles (podemos usar la ecuación para predecir \(y_{T+1}\) porque \(x_T\) es conocido en el tiempo \(T\)).

7.2 Ajuste de Tendencias en el Tiempo

Comprendiendo Patrones en el Tiempo

Predecir se trata de estimar realizaciones futuras de una serie temporal. A lo largo de los años, los analistas han encontrado útil descomponer una serie en tres tipos de patrones: tendencias en el tiempo (\(T_t\)), estacionalidad (\(S_t\)) y patrones aleatorios o irregulares (\(\varepsilon_t\)). Una serie puede ser pronosticada extrapolando cada uno de estos tres patrones. La tendencia es la parte de una serie que corresponde a una evolución lenta y a largo plazo. Esta es la parte más importante para los pronósticos a largo plazo. La parte estacional de la serie corresponde a aspectos que se repiten periódicamente, como cada año. Los patrones irregulares de una serie son movimientos a corto plazo que típicamente son más difíciles de anticipar.

Los analistas generalmente combinan estos patrones de dos maneras: de forma aditiva,
\[\begin{equation} y_t = T_t + S_t + \varepsilon_t, \tag{7.1} \end{equation}\] o de forma multiplicativa,
\[\begin{equation} y_t = T_t \times S_t + \varepsilon_t. \tag{7.2} \end{equation}\]
Los modelos sin componentes estacionales pueden manejarse fácilmente usando \(S_t=0\) para el modelo aditivo en la ecuación (7.1) y \(S_t=1\) para el modelo multiplicativo en la ecuación (7.2). Si el modelo es puramente multiplicativo, como en \(y_t = T_t \times S_t \times \varepsilon_t\), este puede convertirse en un modelo aditivo al tomar logaritmos de ambos lados.

Es instructivo ver cómo estos tres componentes pueden combinarse para formar una serie de interés. Consideremos los tres componentes en la Figura 7.2. Bajo el modelo aditivo, la tendencia, la estacionalidad y la variación aleatoria se combinan para formar la serie que aparece en el panel inferior derecho. Un gráfico de \(y_t\) frente a \(t\) se llama un gráfico de serie temporal. En los gráficos de series temporales, la convención es conectar puntos adyacentes usando una línea para ayudar a detectar patrones en el tiempo.

Cuando analizamos datos, el gráfico en el panel inferior derecho es el primer tipo de gráfico que examinamos. El objetivo del análisis es retroceder: queremos descomponer la serie en sus tres componentes. Cada componente puede ser pronosticado, lo que nos proporcionará pronósticos razonables y fáciles de interpretar.

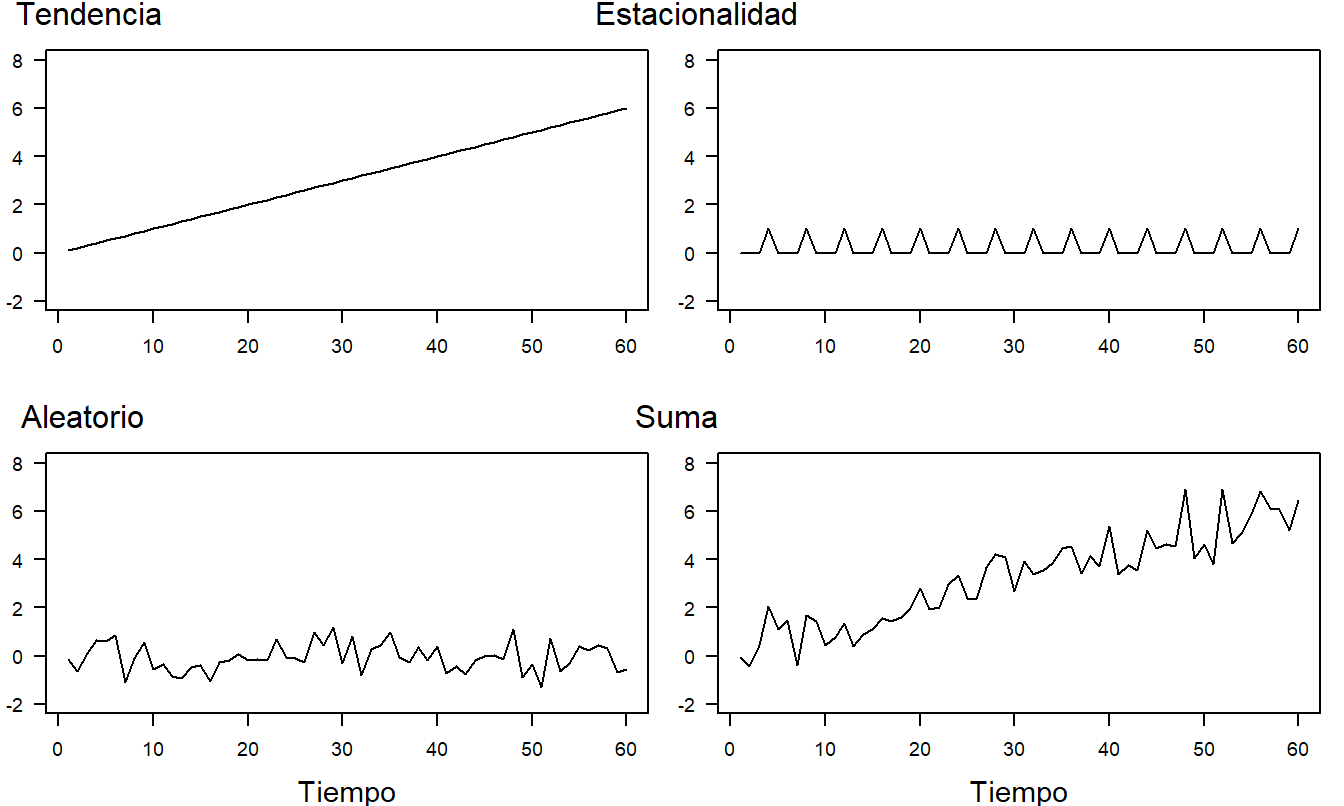
Gráficos de Series Temporales de los Componentes de Respuesta. El componente de tendencia lineal aparece en el panel superior izquierdo, la estacionalidad en el superior derecho y la variación aleatoria en el inferior izquierdo. La suma de los tres componentes aparece en el panel inferior derecho.

Figura 7.2: Gráficos de Series Temporales de los Componentes de Respuesta. El componente de tendencia lineal aparece en el panel superior izquierdo, la estacionalidad en el superior derecho y la variación aleatoria en el inferior izquierdo. La suma de los tres componentes aparece en el panel inferior derecho.

Ajuste de Tendencias en el Tiempo

El tipo más simple de tendencia temporal es la ausencia completa de tendencia. Suponiendo que las observaciones son idénticamente y distribuidas de manera independiente (i.i.d.), entonces podríamos usar el modelo: \[ y_t = \beta_0 + \varepsilon_t. \] Por ejemplo, si estás observando un juego de azar como las apuestas realizadas en el lanzamiento de dos dados, entonces típicamente modelamos esto como una serie i.i.d..

Ajustar funciones polinomiales del tiempo es otro tipo de tendencia que es fácil de interpretar y ajustar a los datos. Comenzamos con una línea recta para nuestra función polinómica del tiempo, lo que da como resultado el modelo de tendencia lineal en el tiempo: \[\begin{equation} y_t = \beta_0 + \beta_1 t + \varepsilon_t. \tag{7.3} \end{equation}\] De manera similar, las técnicas de regresión pueden usarse para ajustar otras funciones que representan tendencias en el tiempo. La ecuación (7.3) se puede extender fácilmente para manejar una tendencia cuadrática en el tiempo: \[ y_t = \beta_0 + \beta_1 t + \beta_2 t^2 + \varepsilon_t, \] o un polinomio de orden superior.

Ejemplo: Tipos de Cambio en Hong Kong. Para los viajeros y empresas, los tipos de cambio son una parte importante de la economía monetaria. El tipo de cambio que consideramos es el número de dólares de Hong Kong que se pueden comprar con un dólar estadounidense. Tenemos \(T=502\) observaciones diarias para el período del 1 de abril de 2005 al 31 de mayo de 2007, obtenidas del informe H10 de la Reserva Federal. La Figura 7.3 muestra un gráfico de serie temporal del tipo de cambio en Hong Kong.

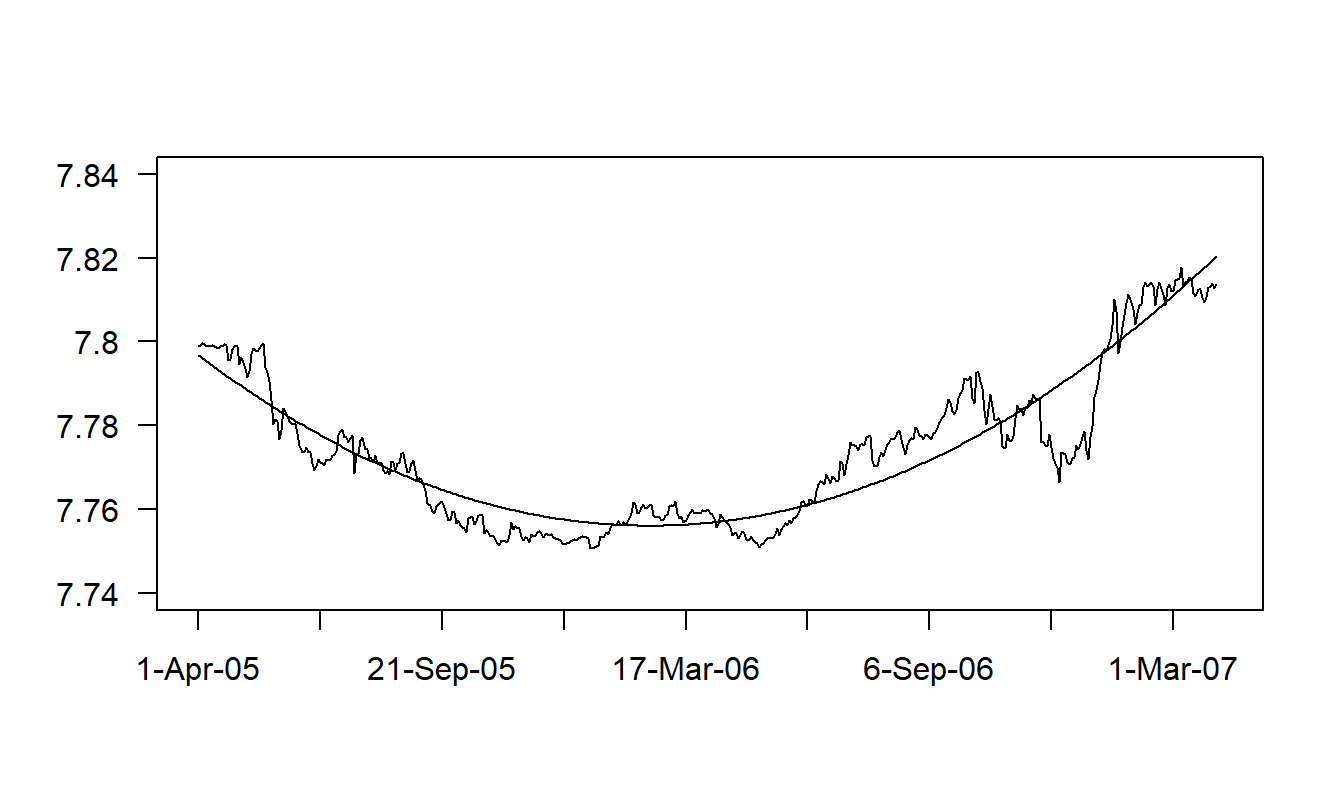
Gráfico de Serie Temporal de los Tipos de Cambio en Hong Kong con Valores Ajustados Superpuestos. Los valores ajustados provienen de una regresión utilizando una tendencia cuadrática en el tiempo. Fuente: Tipos de Cambio Extranjeros (Reserva Federal, informe H10).

Figura 7.3: Gráfico de Serie Temporal de los Tipos de Cambio en Hong Kong con Valores Ajustados Superpuestos. Los valores ajustados provienen de una regresión utilizando una tendencia cuadrática en el tiempo. Fuente: Tipos de Cambio Extranjeros (Reserva Federal, informe H10).

R Code to Produce Figure 7.3

La Figura 7.3 muestra una clara tendencia cuadrática en los datos. Para manejar esta tendencia, usamos \(t=1,...,502\) como una variable explicativa para indicar el período de tiempo. La ecuación de regresión ajustada resulta ser: \[ \begin{array}{cccc} \widehat{INDEX}_t = & 7.797 & -3.68\times 10^{-4}t & +8.269\times 10^{-7}t^2 \\ {\small t\text{-estadísticas}} & {\small (8,531.9)} & {\small (-44.0)} & {\small (51.2)} \end{array} . \]
El coeficiente de determinación es un saludable \(R^2=86.2\%\) y la estimación de la desviación estándar ha disminuido de \(s_{y}=0.0183\) a \(s=0.0068\) (nuestra desviación estándar residual). La Figura 7.3 muestra la relación entre los datos y los valores ajustados mediante el gráfico de serie temporal del tipo de cambio con los valores ajustados superpuestos. Para aplicar estos resultados de regresión al problema de pronóstico, supongamos que queremos predecir el tipo de cambio para el 1 de abril de 2007, o \(t=503\). Nuestra predicción es \[ \widehat{INDEX}_{503} = 7.797 - 3.68 \times 10^{-4}(503) + 8.269 \times 10^{-7}(503)^2 = 7.8208. \]

La conclusión general es que el modelo de regresión que utiliza un término cuadrático en el tiempo \(t\) como variable explicativa ajusta bien los datos. Sin embargo, una inspección más detallada de la Figura 7.3 revela patrones en los residuos, donde las respuestas en algunos lugares son consistentemente más altas y en otros consistentemente más bajas que los valores ajustados. Estos patrones sugieren que podemos mejorar la especificación del modelo. Una forma sería introducir un modelo polinómico de mayor orden en el tiempo. En la Sección 7.3, argumentaremos que el paseo aleatorio es un modelo aún mejor para estos datos.

Otras funciones no lineales del tiempo también pueden ser útiles. Para ilustrar, podríamos estudiar alguna medida de las tasas de interés a lo largo del tiempo (\(y_t\)) y estar interesados en el efecto de un cambio en la economía (como el inicio de una guerra). Definimos \(z_t\) como una variable binaria que es cero antes de que ocurra el cambio y uno durante y después del cambio. Consideremos el modelo, \[\begin{equation} y_t = \beta_0 + \beta_1 z_t + \varepsilon_t. \tag{7.4} \end{equation}\] Así, usando \[ \mathrm{E~}y_t = \left\{ \begin{array}{ll} \beta_0 + \beta_1 & \text{si }z_t=1 \\ \beta_0 & \text{si }z_t = 0 \end{array} \right. , \] el parámetro \(\beta_1\) captura el cambio esperado en las tasas de interés debido al cambio en la economía. Ver Figura 7.4.

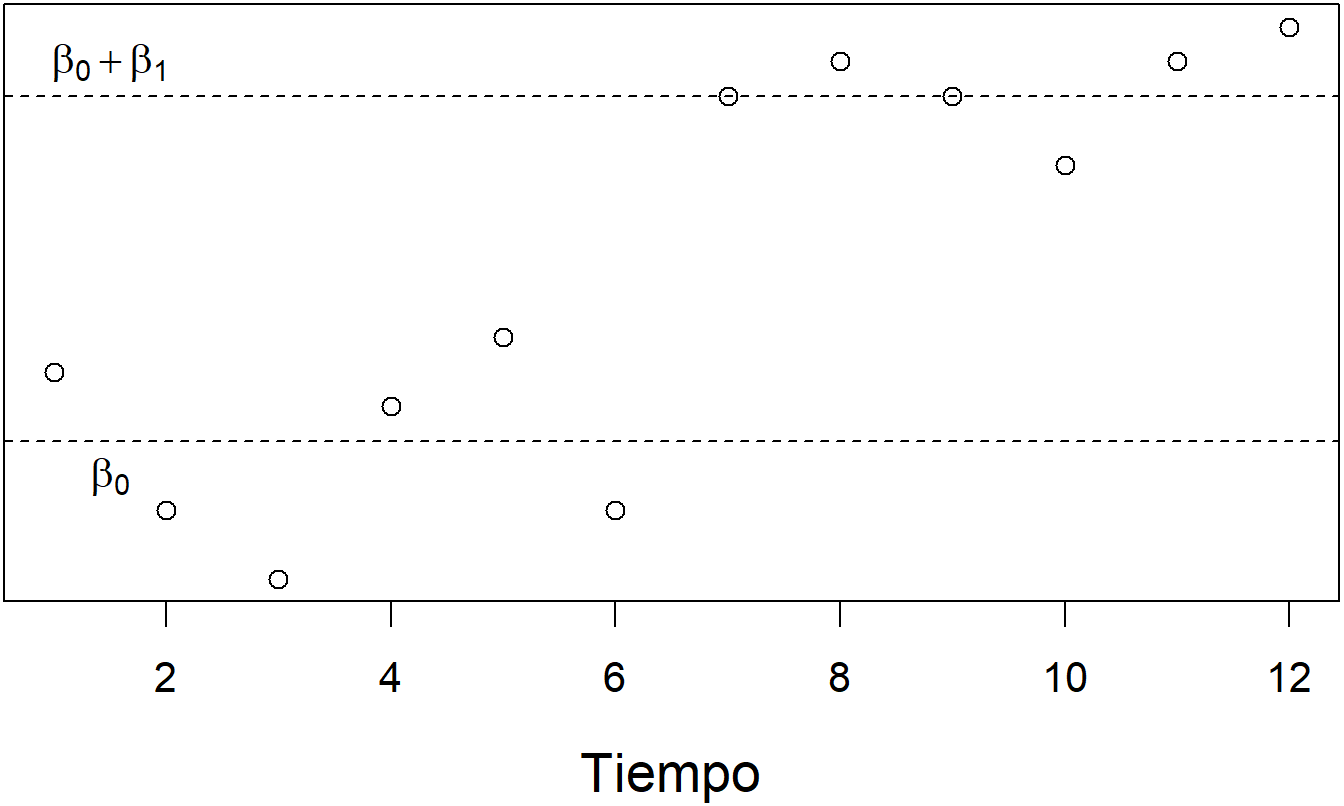
Gráfico de Serie Temporal de Tasas de Interés. Hay un cambio claro en las tasas debido a un cambio en la economía. Este cambio puede medirse usando un modelo de regresión con una variable explicativa que indique el cambio.

Figura 7.4: Gráfico de Serie Temporal de Tasas de Interés. Hay un cambio claro en las tasas debido a un cambio en la economía. Este cambio puede medirse usando un modelo de regresión con una variable explicativa que indique el cambio.

Ejemplo: Modelos de Cambio de Régimen para Retornos de Acciones a Largo Plazo. Con la suposición de normalidad, podemos escribir el modelo en la ecuación (7.4) como \[ y_t \sim \left\{ \begin{array}{ll} N(\mu_1, \sigma^2) & t < t_0 \\ N(\mu_2, \sigma^2)& t \geq t_0 \end{array} \right. , \] donde \(\mu_1 = \beta_0\), \(\mu_2 = \beta_0 + \beta_1\) y \(t_0\) es el punto de cambio. Un modelo de cambio de régimen generaliza este concepto, principalmente al asumir que el punto de cambio no es conocido. En su lugar, se supone que existe un mecanismo de transición que nos permite pasar de un “régimen” a otro con una probabilidad que típicamente se estima a partir de los datos. En este modelo, hay un número finito de estados, o “regímenes.” Dentro de cada régimen, se especifica un modelo probabilístico, como la distribución normal (condicionalmente) independiente (\(N(\mu_2, \sigma^2)\)). También se podría especificar un modelo autorregresivo o autorregresivo condicional que definiremos en el Capítulo 8. Además, existe una probabilidad condicional de transición de un estado a otro (las llamadas probabilidades de transición “Markov”).

Hardy (2001) introdujo los modelos de cambio de régimen en la literatura actuarial, donde la variable dependiente de interés era el retorno del mercado de valores a largo plazo medido por los retornos mensuales en (1) el Standard and Poor’s 500 y (2) el Toronto Stock Exchange 300. Hardy consideró modelos de dos y tres regímenes para datos del período de 1956 a 1999, inclusive. Hardy mostró cómo usar las estimaciones de los parámetros del modelo de cambio de régimen para calcular precios de opciones y medidas de riesgo para contratos de seguros vinculados a acciones.

Ajuste de Tendencias Estacionales

El comportamiento periódico regular a menudo se encuentra en datos económicos y empresariales. Debido a que esta periodicidad a menudo está ligada al clima, estas tendencias se llaman componentes estacionales. Las tendencias estacionales pueden modelarse usando las mismas técnicas que las tendencias regulares o aperiódicas. El siguiente ejemplo muestra cómo capturar el comportamiento periódico utilizando variables binarias estacionales.

Ejemplo: Tendencias en el Voto. En cualquier día de elecciones, el número de votantes que realmente acuden a las urnas depende de varios factores: la publicidad que haya recibido la elección, los temas debatidos como parte de la contienda, otros problemas que enfrenten los votantes el día de las elecciones y factores no políticos, como el clima. Ahora, los posibles candidatos políticos basan sus proyecciones de financiación de campañas y probabilidades de ganar una elección en pronósticos del número de votantes que participarán en una elección. Las decisiones sobre si participar o no como candidato deben tomarse con mucha anticipación; en general, tanto tiempo antes que factores conocidos como el clima en el día de la elección no puedan usarse para generar pronósticos.

Consideramos aquí el número de votantes de Wisconsin que participaron en elecciones estatales durante el período de 1920 a 1990. Aunque el interés radica en pronosticar el número real de votantes, consideramos a los votantes como un porcentaje del público votante calificado. Dividir por el público votante calificado controla el tamaño de la población de votantes; esto mejora la comparabilidad entre las partes iniciales y finales de la serie. Dado que las tendencias de mortalidad son relativamente estables, se pueden obtener fácilmente proyecciones confiables del público votante calificado. Los pronósticos del porcentaje pueden multiplicarse por las proyecciones del público votante para obtener pronósticos de la participación real de votantes.

Para especificar un modelo, examinamos la Figura 7.5, un gráfico de serie temporal de la participación de votantes como porcentaje del público votante calificado. Esta figura muestra la baja participación de votantes en la parte inicial de la serie, seguida de una mayor participación en las décadas de 1950 y 1960, y una menor participación en la década de 1980. Este patrón puede modelarse usando, por ejemplo, una tendencia cuadrática en el tiempo. La figura también muestra una participación mucho mayor en años de elecciones presidenciales. Este componente periódico, o estacional, puede modelarse utilizando una variable binaria. Un modelo candidato es \[ y_t=\beta_0+\beta_1t+\beta_2t^2+\beta_{3}z_t+\varepsilon _t, \] donde

\[ z_t=\left\{ \begin{array}{ll} 1 & \text{si año de elección presidencial} \\ 0 & \text{en caso contrario} \end{array} \right. . \] Aquí, \(\beta_{3}z_t\) captura el componente estacional en este modelo.

Se utilizó regresión para ajustar el modelo. El modelo ajustado proporcionó un buen ajuste a los datos: el coeficiente de determinación fue \(R^2=89.6\%.\) La Figura 7.5 muestra una fuerte relación entre los valores ajustados y los reales.

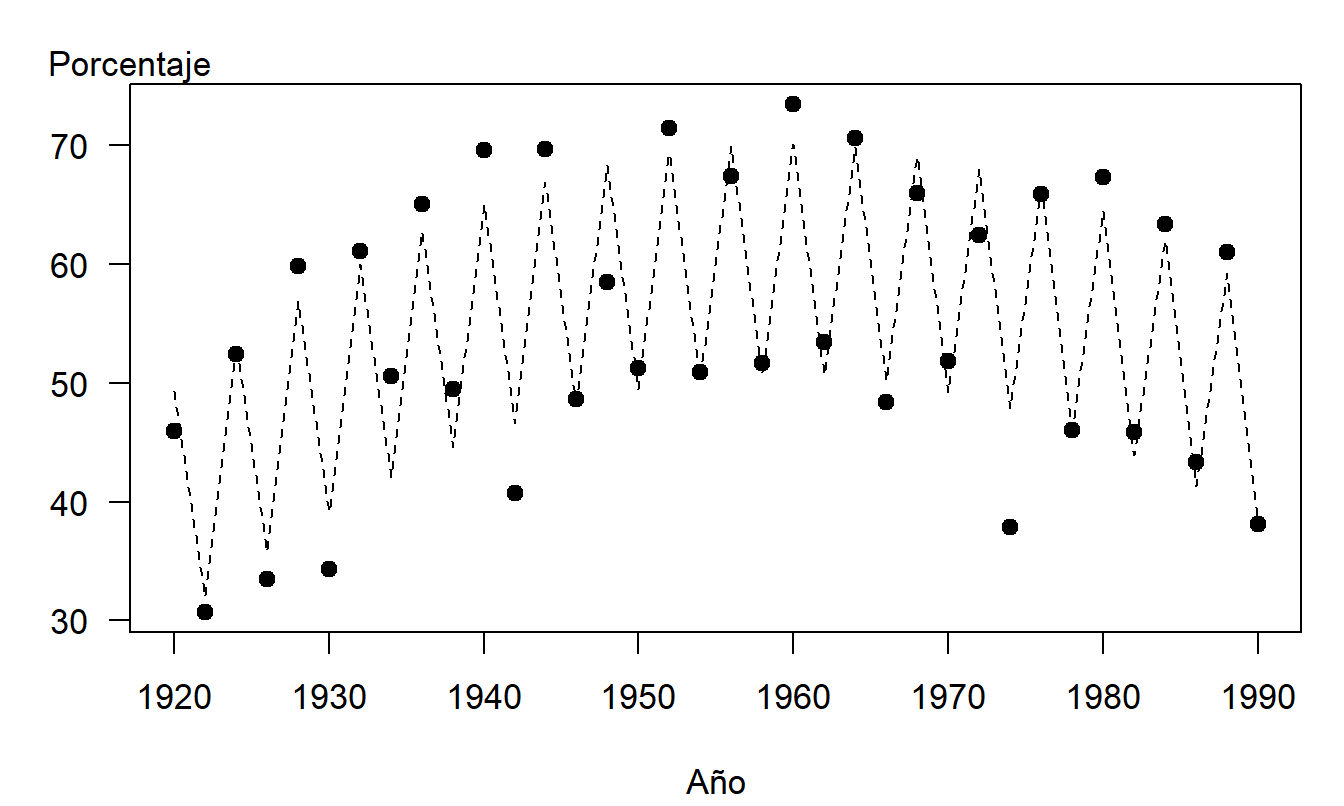
Votantes de Wisconsin como Porcentaje del Público Votante Calificado, por Año. Los círculos opacos representan los porcentajes reales de votación. Las líneas discontinuas representan la tendencia ajustada, utilizando una tendencia cuadrática en el tiempo más una variable binaria para indicar un año de elección presidencial.

Figura 7.5: Votantes de Wisconsin como Porcentaje del Público Votante Calificado, por Año. Los círculos opacos representan los porcentajes reales de votación. Las líneas discontinuas representan la tendencia ajustada, utilizando una tendencia cuadrática en el tiempo más una variable binaria para indicar un año de elección presidencial.

El ejemplo de la tendencia en el voto demuestra el uso de variables binarias para capturar componentes estacionales. De manera similar, los efectos estacionales también pueden representarse utilizando variables categóricas, como \[ z_t=\left\{ \begin{array}{ll} 1 & \text{si primavera} \\ 2 & \text{si verano} \\ 3 & \text{si otoño} \\ 4 & \text{si invierno}. \end{array} \right. \]

Otra forma de capturar efectos estacionales es mediante el uso de funciones trigonométricas. Se discute más sobre el uso de funciones trigonométricas para manejar componentes estacionales en la Sección 9.3.

La eliminación de patrones estacionales se conoce como ajuste estacional. Esta estrategia es apropiada en situaciones de políticas públicas donde el interés radica en interpretar la “serie ajustada estacionalmente” resultante. Por ejemplo, las agencias gubernamentales generalmente informan los ingresos de manufactura industrial en términos de números ajustados estacionalmente, bajo el entendimiento de que los patrones relacionados con feriados y clima se consideran al informar el crecimiento. Sin embargo, para la mayoría de las aplicaciones actuariales y de gestión de riesgos, el interés suele estar en pronosticar la variación de toda la serie, no solo la parte ajustada estacionalmente.

Confiabilidad de los Pronósticos de Series Temporales

Los pronósticos de series temporales a veces se denominan pronósticos “ingenuos”. El adjetivo “ingenuo” es algo irónico porque muchas técnicas de pronóstico de series temporales son técnicas por naturaleza y complejas de calcular. Sin embargo, estos pronósticos se basan en la extrapolación de una única serie de observaciones. Por lo tanto, son ingenuos en el sentido de que los pronósticos ignoran otras fuentes de información que pueden estar disponibles para el pronosticador y los usuarios de los pronósticos. A pesar de ignorar esta información posiblemente importante, los pronósticos de series temporales son útiles porque proporcionan un punto de referencia objetivo con el cual comparar otros pronósticos y opiniones de expertos.

Los pronósticos deben proporcionar al usuario una idea de la confiabilidad del pronóstico. Una forma de cuantificar esto es proporcionar pronósticos bajo conjuntos de supuestos “bajo-intermedio-alto”. Por ejemplo, si estamos pronosticando la deuda nacional, podríamos hacerlo bajo tres escenarios del desempeño futuro de la economía. Alternativamente, podemos calcular intervalos de predicción utilizando muchos de los modelos de pronóstico que se discuten en este texto. Los intervalos de predicción proporcionan una medida de confiabilidad que puede interpretarse en un sentido probabilístico familiar. Además, al variar el nivel de confianza deseado, los intervalos de predicción varían, permitiéndonos responder a preguntas del tipo “¿qué pasaría si…?”.

Por ejemplo, en la Figura 21.10 encontrará una comparación de proyecciones “bajo-intermedio-alto” con intervalos de predicción para pronósticos de la tasa de inflación (IPC) utilizados en la proyección de fondos de la Seguridad Social. Las proyecciones “bajo-intermedio-alto” se basan en un rango de opiniones de expertos y, por lo tanto, reflejan la variabilidad de los pronosticadores. Los intervalos de predicción reflejan la incertidumbre de innovación en el modelo (asumiendo que el modelo es correcto). Ambos rangos dan al usuario una idea de la confiabilidad de los pronósticos, aunque de maneras diferentes.

Los intervalos de predicción tienen la ventaja adicional de cuantificar el hecho de que los pronósticos se vuelven menos confiables cuanto más lejos proyectamos en el futuro. Incluso con datos de corte transversal, vimos que cuanto más lejos estábamos de la parte principal de los datos, menos confiados nos sentíamos en nuestras predicciones. Esto también es cierto al pronosticar datos longitudinales. Es importante comunicar esto a los consumidores de pronósticos, y los intervalos de predicción son una forma conveniente de hacerlo.

En resumen, el análisis de regresión utilizando varias funciones del tiempo como variables explicativas es una herramienta simple pero poderosa para pronosticar datos longitudinales. Sin embargo, tiene desventajas. Debido a que ajustamos una curva a todo el conjunto de datos, no hay garantía de que el ajuste para la parte más reciente de los datos sea adecuado. Es decir, para el pronóstico, la principal preocupación es la parte más reciente de la serie. Sabemos que las estimaciones de análisis de regresión dan más peso a las observaciones con valores inusualmente grandes de variables explicativas. Para ilustrar, usando un modelo de tendencia lineal en el tiempo, esto significa dar más peso a las observaciones al final y al principio de la serie. Usar un modelo que dé mucho peso a las observaciones al principio de la serie se ve con sospecha por los pronosticadores. Esta desventaja del análisis de regresión nos motiva a introducir herramientas adicionales para el pronóstico. (La Sección 9.1 desarrolla este punto con mayor detalle.)

7.3 Estacionariedad y Modelos de Paseo Aleatorio

Una preocupación básica con los procesos que evolucionan a lo largo del tiempo es la estabilidad del proceso. Por ejemplo: “¿Me toma más tiempo llegar al trabajo desde que instalaron el nuevo semáforo?” “¿Han mejorado las ganancias trimestrales desde que el nuevo CEO asumió el cargo?” Medimos procesos para mejorar o gestionar su desempeño y para pronosticar el futuro del proceso. Dado que la estabilidad es una preocupación fundamental, trabajaremos con un tipo especial de estabilidad llamado estacionariedad.

Definición. La estacionariedad es el concepto matemático formal que corresponde a la “estabilidad” de una serie temporal de datos. Se dice que una serie es (débilmente) estacionaria si:

  • la media \(\mathrm{E~}y_t\) no depende de \(t\), y
  • la covarianza entre \(y_{s}\) y \(y_t\) depende solo de la diferencia entre las unidades de tiempo, \(|t-s|.\)

Por lo tanto, por ejemplo, bajo estacionariedad débil \(\mathrm{E~}y_{4}=\mathrm{E~}y_{8}\) porque las medias no dependen del tiempo y, por lo tanto, son iguales. Además, \(\mathrm{Cov}(y_{4},y_{6})=\mathrm{Cov}(y_{6},y_{8})\), porque \(y_{4}\) y \(y_{6}\) están separados por dos unidades de tiempo, al igual que \(y_{6}\) y \(y_{8}\). Como otra implicación de la segunda condición, note que \(\sigma^2 = \mathrm{Cov}(y_t, y_t)\) \(= \mathrm{Cov}(y_s, y_s) = \sigma^2\). Por lo tanto, una serie débilmente estacionaria tiene una media constante y una varianza constante (homocedástica). Otro tipo de estacionariedad conocido como estricta o fuerte requiere que toda la distribución de \(y_t\) sea constante en el tiempo, no solo la media y la varianza.

Ruido Blanco

El vínculo entre los modelos longitudinales y transversales puede establecerse mediante la noción de un proceso de ruido blanco. Un proceso de ruido blanco es un proceso estacionario que no muestra patrones evidentes a lo largo del tiempo. Más formalmente, un proceso de ruido blanco es simplemente una serie que es i.i.d., idéntica e independientemente distribuida. Un proceso de ruido blanco es solo un tipo de proceso estacionario: el Capítulo 8 introducirá otro tipo, un modelo autorregresivo.

Una característica especial del proceso de ruido blanco es que los pronósticos no dependen de cuán lejos en el futuro deseemos pronosticar. Supongamos que una serie de observaciones, \(y_1,...,y_T\), ha sido identificada como un proceso de ruido blanco. Sean \(\overline{y}\) y \(s_y\) la media muestral y la desviación estándar muestral, respectivamente. Un pronóstico de una observación en el futuro, digamos \(y_{T+l}\), para \(l\) unidades de tiempo hacia adelante, es \(\overline{y}\). Además, un intervalo de pronóstico es \[\begin{equation} \overline{y}\pm \ t_{T-1,1-\alpha/2} ~ s_y \sqrt{1+\frac{1}{T}}. \tag{7.5} \end{equation}\] En aplicaciones de series temporales, dado que el tamaño de la muestra \(T\) suele ser relativamente grande, utilizamos el intervalo de predicción aproximado del 95% \(\overline{y} \pm 2 s_y\). Este intervalo de pronóstico aproximado ignora la incertidumbre del parámetro al usar \(\overline{y}\) y \(s_y\) para estimar la media \(\mathrm{E}~y\) y la desviación estándar \(\sigma\) de la serie. En cambio, enfatiza la incertidumbre en las realizaciones futuras de la serie (conocida como incertidumbre de innovación). Tenga en cuenta que este intervalo no depende de la elección de \(l\), el número de unidades de tiempo hacia adelante que pronosticamos.

El modelo de ruido blanco es el menos y el más importante de los modelos de series temporales. Es el menos importante en el sentido de que el modelo asume que las observaciones no están relacionadas entre sí, un evento poco probable para la mayoría de las series de interés. Es el más importante porque nuestros esfuerzos de modelado están dirigidos a reducir una serie a un proceso de ruido blanco. En el análisis de series temporales, el procedimiento para reducir una serie a un proceso de ruido blanco se llama filtro. Una vez que se han filtrado todos los patrones de los datos, se dice que la incertidumbre es irreductible.

Paseo Aleatorio

Ahora introducimos el modelo de paseo aleatorio. Para este modelo de series temporales, mostraremos cómo filtrar los datos simplemente tomando diferencias.

Para ilustrar, supongamos que juegas un juego simple basado en el lanzamiento de dos dados. Para jugar, debes pagar $7 cada vez que lanzas los dados. Recibes el número de dólares correspondiente a la suma de los dos dados, \(c_t^{\ast}\). Sea \(c_t\) tus ganancias en cada lanzamiento, de modo que \(c_t = c_t^{\ast} - 7\). Suponiendo que los lanzamientos son independientes y provienen de la misma distribución, la serie \(\{c_t\}\) es un proceso de ruido blanco.

Supongamos que comienzas con un capital inicial de \(y_0 = \$100\). Sea \(y_t\) la suma del capital después del lanzamiento \(t\). Note que \(y_t\) se determina recursivamente como \(y_t = y_{t-1} + c_t\). Por ejemplo, porque ganaste $3 en el primer lanzamiento, \(t=1\), ahora tienes un capital de \(y_1 = y_0 + c_1\), o 103 = 100 + 3. Tabla 7.1 muestra los resultados de los primeros cinco lanzamientos. La Figura 7.6 es un gráfico de series temporales de las sumas, \(y_t\), para los cincuenta lanzamientos.

Tabla 7.1. Ganancias para Cinco de los 50 Lanzamientos

\[ \begin{array}{c|ccccc} \hline t & 1 & 2 & 3 & 4 & 5 \\ c_t^{\ast } & 10 & 9 & 7 & 5 & 7 \\ c_t & 3 & 2 & 0 & -2 & 0 \\ ~~y_t~~ & ~103~ & ~105~ & ~105~ & ~103~ & 103 \\ \hline \end{array} \]

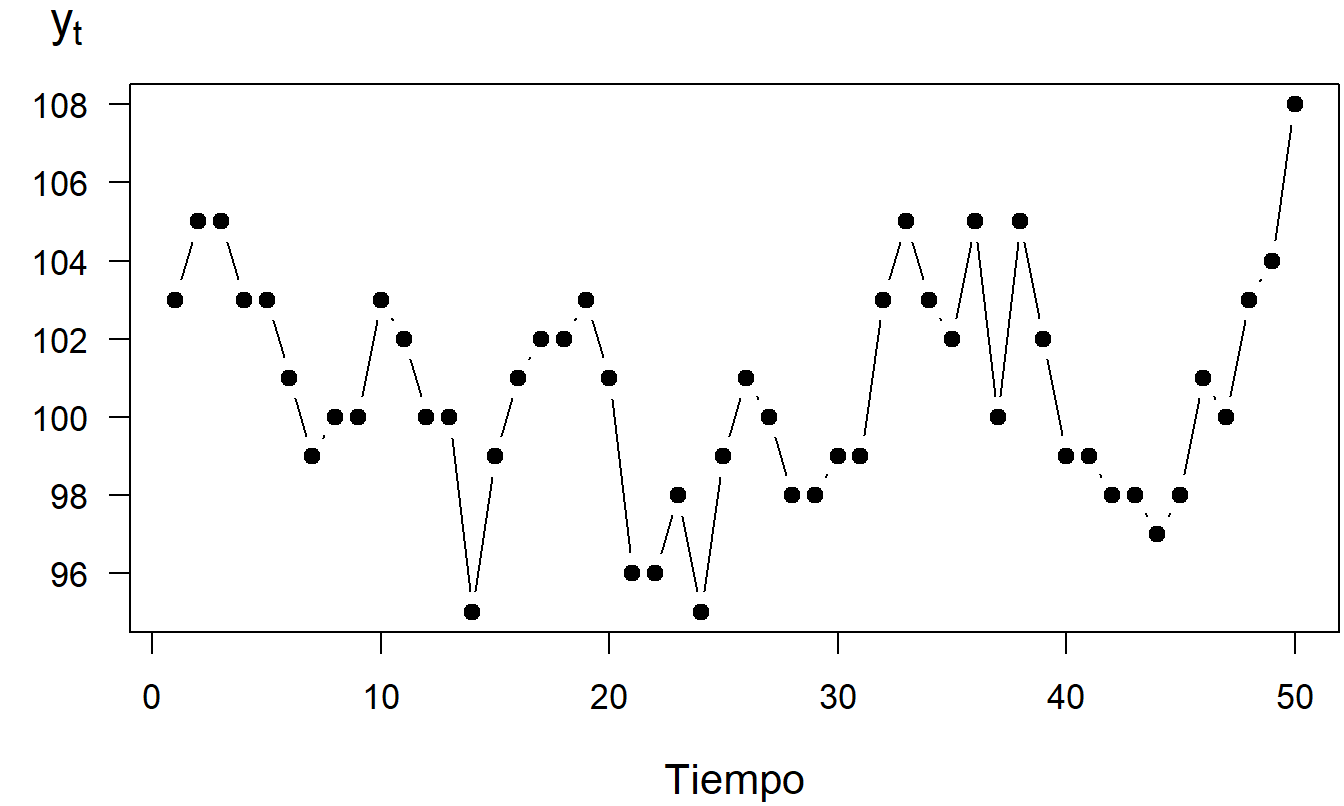
Gráfico de Series Temporales de la Suma del Capital

Figura 7.6: Gráfico de Series Temporales de la Suma del Capital

Las sumas parciales de un proceso de ruido blanco definen un modelo de paseo aleatorio. Por ejemplo, la serie \(\{y_1, \ldots ,y_{50}\}\) en la Figura 7.6 es una realización del modelo de paseo aleatorio. La frase suma parcial se utiliza porque cada observación, \(y_t\), se creó sumando las ganancias hasta el tiempo \(t\). En este ejemplo, las ganancias, \(c_t\), son un proceso de ruido blanco porque el monto retornado, \(c_t^{\ast}\), es i.i.d. En nuestro ejemplo, tus ganancias de cada lanzamiento de los dados se representan mediante un proceso de ruido blanco. Si ganas en un lanzamiento de los dados no influye en el resultado del siguiente o del anterior lanzamiento. En contraste, tu cantidad de capital en cualquier lanzamiento de los dados está altamente relacionada con la cantidad de capital después del siguiente o anterior lanzamiento. Tu cantidad de capital después de cada lanzamiento de los dados se representa mediante un modelo de paseo aleatorio.

7.4 Inferencia usando Modelos de Paseo Aleatorio

El paseo aleatorio es un modelo de series temporales de uso común. Para ver cómo se puede aplicar, primero discutimos algunas propiedades del modelo. Luego, utilizamos estas propiedades para pronosticar e identificar una serie como un paseo aleatorio. Finalmente, esta sección compara el paseo aleatorio con un competidor, el modelo de tendencia lineal en el tiempo.

Propiedades del Modelo

Para establecer las propiedades del paseo aleatorio, primero recapitulamos algunas definiciones. Sean \(c_1,\ldots ,c_T\) \(T\) observaciones de un proceso de ruido blanco. Un paseo aleatorio puede expresarse recursivamente como \[\begin{equation} y_t = y_{t-1} + c_t. \tag{7.6} \end{equation}\] Por sustitución repetida, tenemos \[ y_t = c_t + y_{t-1} = c_t + \left( c_{t-1} + y_{t-2}\right) = \ldots \] Si usamos \(y_0\) como el nivel inicial, entonces podemos expresar el paseo aleatorio como \[\begin{equation} y_t = y_0 + c_1 + \ldots + c_t. \tag{7.7} \end{equation}\] La ecuación (7.7) muestra que un paseo aleatorio es la suma parcial de un proceso de ruido blanco.

El paseo aleatorio no es un proceso estacionario porque la variabilidad, y posiblemente la media, depende del punto de tiempo en el que se observa la serie. Tomando la esperanza y la varianza de la ecuación (7.7), obtenemos el nivel medio y la variabilidad del proceso de paseo aleatorio: \[ \mathrm{E~}y_t = y_0 + t\mu_c\ \ \text{ y} \ \ \mathrm{Var~} y_t = t \sigma_c^2, \] donde \(\mathrm{E~}c_t = \mu_c\) y \(\mathrm{Var~}c_t = \sigma _c^2\). Por lo tanto, mientras haya alguna variabilidad en el proceso de ruido blanco (\(\sigma_c^2 > 0\)), el paseo aleatorio no es estacionario en la varianza. Además, si \(\mu_c\neq 0\), entonces el paseo aleatorio no es estacionario en la media.

Pronósticos

¿Cómo podemos pronosticar una serie de observaciones, \(y_1,...,y_T\), que ha sido identificada como una realización de un modelo de paseo aleatorio? La técnica que usamos es pronosticar las diferencias, o cambios, en la serie y luego sumar las diferencias pronosticadas para obtener la serie pronosticada. Esta técnica es manejable porque, por definición del modelo de paseo aleatorio, las diferencias pueden representarse utilizando un proceso de ruido blanco, un proceso que sabemos cómo pronosticar.

Consideremos \(y_{T+l}\), el valor de la serie \(l\) unidades de tiempo en el futuro. Sea \(c_t=y_t-y_{t-1}\) que representa las diferencias en la serie, de modo que \[\begin{eqnarray*} y_{T+l} &=&y_{T+l-1}+c_{T+l} = \left( y_{T+l-2} + c_{T+l-1}\right) +c_{T+l} = \ldots \\ &=&y_T+c_{T+1}+ \ldots +c_{T+l}. \end{eqnarray*}\] Interpretamos \(y_{T+l}\) como el valor actual de la serie, \(y_T\), más la suma parcial de diferencias futuras.

Para pronosticar \(y_{T+l}\), dado que en el tiempo \(T\) conocemos \(y_T\), solo necesitamos pronosticar los cambios \(\{c_{T+1}, \ldots, c_{T+l}\}\). Debido a que un pronóstico de un valor futuro de un proceso de ruido blanco es simplemente el promedio del proceso, el pronóstico de \(c_{T+k}\) es \(\overline{c}\) para \(k=1,2,\ldots,l\). Combinando estos resultados, el pronóstico de \(y_{T+l}\) es \(y_T+l\overline{c}\). Por ejemplo, para \(l=1\), interpretamos que el pronóstico del siguiente valor de la serie es el valor actual de la serie más el cambio promedio de la serie.

Usando ideas similares, tenemos que un intervalo de predicción aproximado al 95% para \(y_{T+l}\) es \[ y_T+l\overline{c}\pm 2s_c\sqrt{l} \] donde \(s_c\) es la desviación estándar calculada utilizando los cambios \(c_2,c_{3},\ldots,c_T\). Note que el ancho del intervalo de predicción, \(4 s_c \sqrt{l}\), crece a medida que crece el horizonte de pronóstico \(l\). Este aumento en el ancho simplemente refleja nuestra capacidad decreciente para predecir hacia el futuro.

Como ejemplo, lanzamos los dados \(T=50\) veces y queremos pronosticar \(y_{60}\), nuestra suma de capital después de 60 lanzamientos. En el tiempo 50, resultó que nuestra suma de dinero disponible era \(y_{50}=\$93\). Comenzando con \(y_0 = \$100\), el cambio promedio fue \(\overline{c} = -7/50 = -0.14\), con una desviación estándar \(s_c=\$2.703\). Por lo tanto, el pronóstico en el tiempo 60 es \(93+10(-.14) =91.6\). El correspondiente intervalo de predicción al 95% es \[ 91.6\pm 2\left( 2.703\right) \sqrt{10}=91.6\pm 17.1=\left( 74.5,108.7\right). \]

Ejemplo: Tasas de Participación en la Fuerza Laboral. Los pronósticos de la tasa de participación en la fuerza laboral (\(LFPR\)), junto con pronósticos de la población, nos brindan una visión de la futura fuerza laboral de una nación. Esta visión proporciona información sobre el funcionamiento futuro de la economía en general, y por lo tanto, las proyecciones de \(LFPR\) son de interés para varias agencias gubernamentales. En los Estados Unidos, las tasas de participación en la fuerza laboral son proyectadas por la Administración del Seguro Social, la Oficina de Estadísticas Laborales, la Oficina de Presupuesto del Congreso y la Oficina de Gestión y Presupuesto. En el contexto del Seguro Social, los formuladores de políticas utilizan proyecciones de la fuerza laboral para evaluar propuestas de reforma del sistema de Seguro Social y para evaluar su futura solvencia financiera.

La tasa de participación en la fuerza laboral es la fuerza laboral civil dividida por la población civil no institucionalizada. Estos datos son recopilados por la Oficina de Estadísticas Laborales. Para fines de ilustración, examinemos un grupo demográfico específico y mostremos cómo pronosticarlo; los pronósticos de otros grupos pueden encontrarse en Fullerton (1999) y Frees (2006). Específicamente, examinamos el período 1968-1998 para mujeres de 20 a 44 años, que viven en un hogar con un cónyuge presente y al menos un hijo menor de seis años. La Figura 7.7 muestra el rápido aumento en \(LFPR\) para este grupo a lo largo de \(T=31\) años.

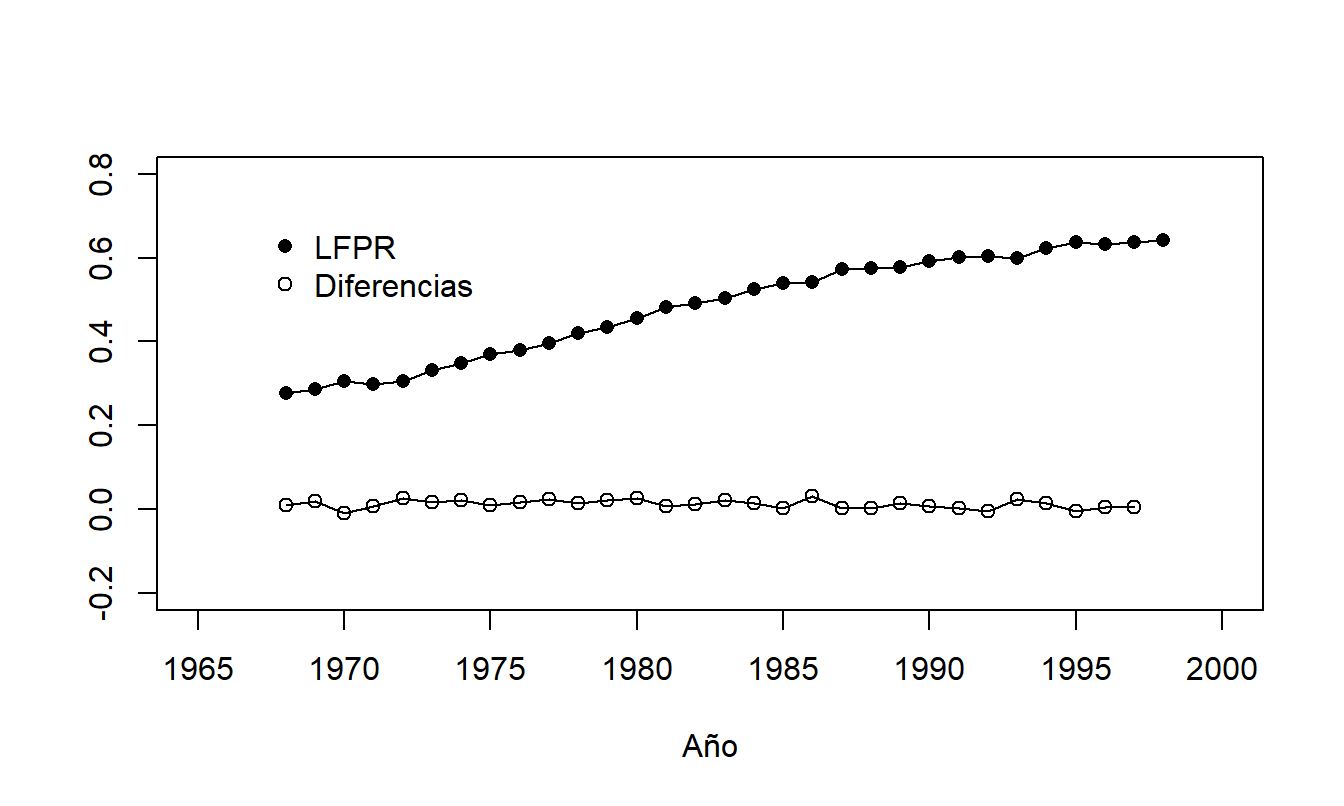
Tasas de Participación en la Fuerza Laboral para Mujeres de 20-44 años, Viviendo en un Hogar con un Cónyuge Presente y al Menos un Hijo Menor de Seis Años. El gráfico de la serie muestra un rápido aumento con el tiempo. También se muestran las diferencias, que son constantes.

Figura 7.7: Tasas de Participación en la Fuerza Laboral para Mujeres de 20-44 años, Viviendo en un Hogar con un Cónyuge Presente y al Menos un Hijo Menor de Seis Años. El gráfico de la serie muestra un rápido aumento con el tiempo. También se muestran las diferencias, que son constantes.

Código R para producir la Figura 7.7

Para pronosticar el \(LFPR\) con un paseo aleatorio, comenzamos con nuestra observación más reciente, \(LFPR_{31}=0.6407\). Denotamos el cambio en el \(LFPR\) como \(c_t\), de modo que \(c_t=LFPR_t-LFPR_{t-1}\). Resulta que el cambio promedio es \(\overline{c}=0.0121\) con una desviación estándar \(s_c=0.0101\). Así, usando un modelo de paseo aleatorio, un intervalo de predicción aproximado al 95% para el pronóstico de \(l\) pasos es \[ 0.6407+0.0121l\pm \ 0.0202\sqrt{l}. \] La Figura 7.8 ilustra los intervalos de predicción para los años 1999 a 2002, inclusive.

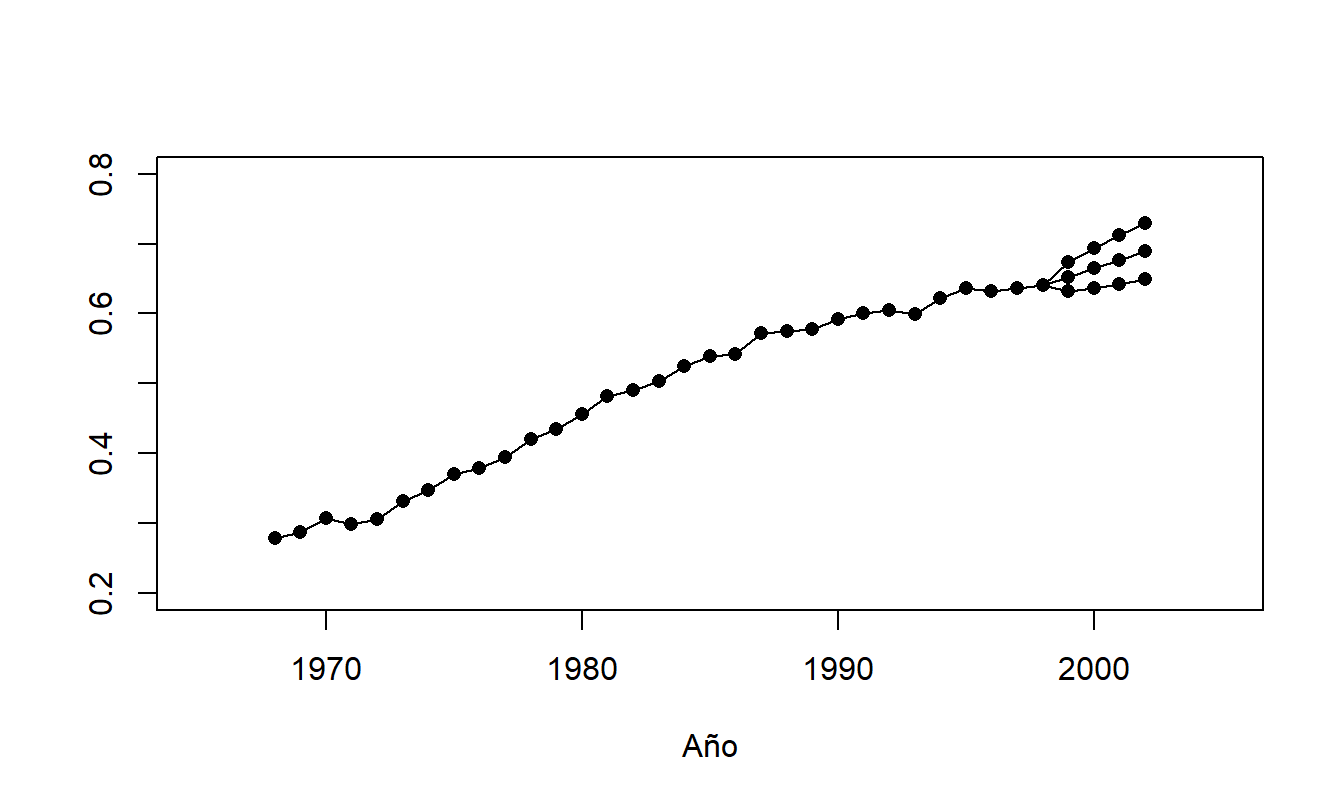
Gráfico de Series Temporales de las Tasas de Participación en la Fuerza Laboral con Valores Pronosticados para 1999-2002. La serie del medio representa los pronósticos puntuales. Las series superior e inferior representan los límites superior e inferior de los intervalos de predicción al 95%. Los datos de 1968-1998 representan valores reales.

Figura 7.8: Gráfico de Series Temporales de las Tasas de Participación en la Fuerza Laboral con Valores Pronosticados para 1999-2002. La serie del medio representa los pronósticos puntuales. Las series superior e inferior representan los límites superior e inferior de los intervalos de predicción al 95%. Los datos de 1968-1998 representan valores reales.

Código R para producir la Figura 7.8

Identificación de Estacionariedad

Hemos visto cómo hacer cosas útiles, como pronósticos, con modelos de paseo aleatorio. Pero, ¿cómo identificamos que una serie es una realización de un paseo aleatorio? Sabemos que el paseo aleatorio es un tipo especial de modelo no estacionario, por lo que el primer paso es examinar una serie y decidir si es estacionaria o no.

La estacionariedad cuantifica la estabilidad de un proceso. Un proceso que es estrictamente estacionario tiene la misma distribución a lo largo del tiempo, por lo que deberíamos poder tomar muestras sucesivas de tamaño modesto y mostrar que tienen aproximadamente la misma distribución. Para la estacionariedad débil, la media y la varianza son estables a lo largo del tiempo, por lo que si tomamos muestras sucesivas de tamaño modesto, esperamos que el nivel promedio y la varianza sean aproximadamente similares. Para ilustrar, al examinar gráficos de series temporales, si miras las primeras cinco observaciones, las siguientes cinco, las siguientes cinco, y así sucesivamente, deberías observar niveles aproximadamente similares de promedios y desviaciones estándar.

En aplicaciones de gestión de calidad, este enfoque se cuantifica mediante el uso de gráficos de control. Un gráfico de control es una herramienta gráfica útil para detectar la falta de estacionariedad en una serie temporal. La idea básica es superponer líneas de referencia llamadas límites de control en un gráfico de series temporales de los datos. Estas líneas de referencia nos ayudan a detectar visualmente tendencias en los datos e identificar puntos inusuales. La mecánica detrás de los límites de control es sencilla. Para una serie de observaciones, calculamos la media y la desviación estándar de la serie, \(\overline{y}\) y \(s_y\). Definimos el “límite superior de control” como \(UCL=\overline{y}+3s_y\) y el “límite inferior de control” como \(LCL=\overline{y}-3s_y\). Los gráficos de series temporales con estos límites de control superpuestos se conocen como gráficos de control.

A veces se asocia el adjetivo retrospectivo con este tipo de gráfico de control. Este adjetivo recuerda al usuario que los promedios y las desviaciones estándar se basan en todos los datos disponibles. En contraste, cuando el gráfico de control se utiliza como una herramienta de gestión continua para detectar si un proceso industrial está “fuera de control”, un gráfico de control prospectivo puede ser más adecuado. Aquí, prospectivo simplemente significa usar solo una porción temprana del proceso, que está “bajo control”, para calcular los límites de control.

Un gráfico de control que nos ayuda a examinar la estabilidad de la media es el gráfico \(Xbar\). Un gráfico \(Xbar\) se crea combinando observaciones sucesivas de tamaño modesto, calculando un promedio sobre este grupo y luego creando un gráfico de control para los promedios de los grupos. Al tomar promedios sobre grupos, la variabilidad asociada con cada punto en el gráfico es menor que la de un gráfico de control para observaciones individuales. Esto permite al analista de datos obtener una imagen más clara de cualquier patrón que pueda ser evidente en la media de la serie.

Un gráfico de control que nos ayuda a examinar la estabilidad de la variabilidad es el gráfico \(R\). Al igual que con el gráfico \(Xbar\), comenzamos formando grupos sucesivos de tamaño modesto. Con el gráfico \(R\), para cada grupo calculamos el rango, que es la observación más grande menos la más pequeña, y luego creamos un gráfico de control para los rangos de los grupos. El rango es una medida de variabilidad simple de calcular, una ventaja importante en aplicaciones de manufactura.

Identificación de Paseos Aleatorios

Supongamos que sospechas que una serie no es estacionaria, ¿cómo identificas que estas son realizaciones de un modelo de paseo aleatorio? Recordemos que el valor esperado de un paseo aleatorio, \(\mathrm{E~}y_t=y_0+t\mu_c\), sugiere que dicha serie sigue una tendencia lineal en el tiempo. La varianza de un paseo aleatorio, \(\mathrm{Var~}y_t=t\sigma_c^2\), sugiere que la variabilidad de una serie aumenta a medida que el tiempo \(t\) crece. Primero, un gráfico de control puede ayudarnos a detectar estos patrones, ya sea una tendencia lineal en el tiempo, una variabilidad creciente, o ambos.

Segundo, si los datos originales siguen un modelo de paseo aleatorio, entonces la serie diferenciada sigue un modelo de proceso de ruido blanco. Si un modelo de paseo aleatorio es un modelo candidato, deberías examinar las diferencias de la serie. En este caso, el gráfico de series temporales de las diferencias debería ser un proceso estacionario, de ruido blanco, que no muestra patrones evidentes. Los gráficos de control pueden ayudarnos a detectar esta ausencia de patrones.

Tercero, compara las desviaciones estándar de la serie original y la serie diferenciada. Esperamos que la desviación estándar de la serie original sea mayor que la desviación estándar de la serie diferenciada. Por lo tanto, si la serie puede representarse mediante un paseo aleatorio, esperamos una reducción sustancial en la desviación estándar al tomar diferencias.

Ejemplo: Tasas de Participación en la Fuerza Laboral - Continuación. En la Figura 7.7, la serie muestra una clara tendencia ascendente mientras que las diferencias no muestran tendencias aparentes en el tiempo. Además, al calcular las diferencias de la serie, resulta que \[ 0.1237=SD(series)>SD(differences)=0.0101. \] Por lo tanto, parece razonable utilizar tentativamente un modelo de paseo aleatorio para la serie de tasas de participación en la fuerza laboral.

En el Capítulo 8, discutiremos dos dispositivos adicionales de identificación. Estos son gráficos de dispersión de la serie frente a una versión rezagada de la serie y las estadísticas resumen correspondientes llamadas autocorrelaciones.

Paseo Aleatorio versus Modelo de Tendencia Lineal en el Tiempo

El ejemplo de la tasa de participación en la fuerza laboral podría representarse usando un paseo aleatorio o un modelo de tendencia lineal en el tiempo. Estos dos modelos están más relacionados entre sí de lo que parece a primera vista. Para ver esta relación, recordemos que el modelo de tendencia lineal en el tiempo puede escribirse como \[\begin{equation} y_t = \beta_0 + \beta_1 t + \varepsilon_t, \tag{7.8} \end{equation}\] donde \(\{\varepsilon_t\}\) es un proceso de ruido blanco. Si \(\{y_t\}\) es un paseo aleatorio, entonces puede modelarse como una suma parcial como en la ecuación (7.7). También podemos descomponer el proceso de ruido blanco en una media \(\mu_c\) más otro proceso de ruido blanco, es decir, \(c_t = \mu_c + \varepsilon_t\). Combinando estas dos ideas, un modelo de paseo aleatorio puede escribirse como \[\begin{equation} y_t = y_0 + \mu_c t + u_t \tag{7.9} \end{equation}\] donde \(u_t = \sum_{j=1}^{t} \varepsilon_j\). Comparando las ecuaciones (7.8) y (7.9), vemos que los dos modelos son similares en que la porción determinística es una función lineal del tiempo. La diferencia está en el componente de error. El componente de error para el modelo de tendencia lineal en el tiempo es un proceso estacionario de ruido blanco. El componente de error para el modelo de paseo aleatorio no es estacionario porque es la suma parcial de procesos de ruido blanco. Es decir, el componente de error también es un paseo aleatorio. Muchos tratamientos introductorios del modelo de paseo aleatorio se centran en el ejemplo del “juego justo” e ignoran el término de deriva \(\mu_c\). Esto es desafortunado porque la comparación entre el modelo de paseo aleatorio y el modelo de tendencia lineal en el tiempo no es tan clara cuando el parámetro \(\mu_c\) es igual a cero.

7.5 Filtrado para Lograr Estacionariedad

Un filtro es un procedimiento para reducir las observaciones a ruido blanco. En regresión, logramos esto simplemente restando la función de regresión de las observaciones, es decir, \(y_i - (\beta_0 + \beta_1 x_{1i} + \ldots + \beta_k x_{ki})=\varepsilon_i\). La transformación de los datos es otro dispositivo para filtrar que introdujimos en el Capítulo 1 al analizar datos de corte transversal. Encontramos otro ejemplo de un filtro en la Sección 7.3. Allí, al tomar diferencias de las observaciones, reducimos una serie de paseo aleatorio a un proceso de ruido blanco.

Un tema importante de este texto es usar un enfoque iterativo para ajustar modelos a datos. En particular, en este capítulo discutimos técnicas para reducir una secuencia de observaciones a una serie estacionaria. Por definición, una serie estacionaria es estable y, por lo tanto, es mucho más fácil de pronosticar que una serie inestable. Esta etapa, a veces conocida como pre-procesamiento de los datos, generalmente da cuenta de las fuentes más importantes de tendencias en los datos. El próximo capítulo presentará modelos que explican tendencias más sutiles en los datos.

Transformaciones

Al analizar datos longitudinales, la transformación es una herramienta importante para filtrar un conjunto de datos. Específicamente, usar una transformación logarítmica tiende a reducir los datos “dispersos”. Esta característica nos da un método alternativo para tratar un proceso donde la variabilidad parece crecer con el tiempo. Recordemos que la primera opción discutida es proponer un modelo de paseo aleatorio y examinar las diferencias de los datos. Alternativamente, se puede tomar una transformación logarítmica que ayuda a reducir la varianza creciente en el tiempo.

Además, por la discusión sobre paseos aleatorios, sabemos que si tanto la varianza de la serie como la varianza de la serie logarítmica aumentan con el tiempo, las diferencias de la transformación logarítmica pueden manejar esta variabilidad creciente. Las diferencias de logaritmos naturales son particularmente útiles porque pueden interpretarse como cambios proporcionales. Para ver esto, definimos \(pchange_t=(y_t/y_{t-1})-1\). Entonces, \[ \ln y_t-\ln y_{t-1} = \ln \left( \frac{y_t}{y_{t-1}}\right) = \ln \left( 1+pchange_t\right) \approx pchange_t. \] Aquí usamos la aproximación de series de Taylor \(\ln (1+x) \approx x\) que es apropiada para valores pequeños de \(|x|\).

Ejemplo: Índice Compuesto Trimestral de Standard and Poor’s. Una tarea importante de un analista financiero es cuantificar costos asociados con flujos de efectivo futuros. Consideramos aquí fondos invertidos en una medida estándar del desempeño general del mercado, el Índice Compuesto S&P 500. El objetivo es pronosticar el desempeño de la cartera para descontar flujos de efectivo.

En particular, examinamos el Índice Compuesto Trimestral de S&P para los años 1936 a 2007, inclusive. Según los estándares actuales, este período puede no ser el más representativo porque incluye la Gran Depresión de la década de 1930. La motivación para analizar estos datos proviene del informe del “Grupo de Trabajo sobre Garantías de Madurez” del Instituto de Actuarios (1980), que analizó la serie de 1936 a 1977, inclusive. Este informe estudió el comportamiento a largo plazo de los rendimientos de inversión desde un punto de vista actuarial. Complementamos ese trabajo mostrando cómo las técnicas gráficas pueden sugerir una transformación útil para reducir los datos a un proceso estacionario.

Los datos se muestran en la Figura 7.9. A partir de los valores originales del índice en el panel superior izquierdo, vemos que el nivel promedio y la variabilidad aumentan con el tiempo. Este patrón indica claramente que la serie no es estacionaria.

Por nuestras discusiones en las Secciones 7.2 y 7.3, un modelo candidato con estas propiedades es el paseo aleatorio. Sin embargo, el gráfico de series temporales de las diferencias, en el panel superior derecho de la Figura 7.9, todavía indica un patrón de variabilidad creciente en el tiempo. Las diferencias no son un proceso de ruido blanco, por lo que el paseo aleatorio no es un modelo adecuado para el Índice S&P 500.

Una transformación alternativa es considerar los valores logarítmicos de la serie. El gráfico de series temporales de los valores logarítmicos, presentado en el panel inferior izquierdo de la Figura 7.9, indica que el nivel promedio de la serie aumenta con el tiempo y no es constante. Por lo tanto, el índice logarítmico no es estacionario.

Otra estrategia es examinar las diferencias de la serie logarítmica. Esto es especialmente deseable al analizar índices o “cestas básicas”, porque la diferencia de logaritmos puede interpretarse como cambios proporcionales. En el gráfico final de series temporales, en el panel inferior derecho de la Figura 7.9, vemos que hay menos patrones discernibles en la serie transformada, la diferencia de logaritmos. Esta serie transformada parece ser estacionaria. Es interesante notar que parece haber un mayor nivel de volatilidad al comienzo de la serie. Este tipo de volatilidad cambiante es más difícil de modelar y ha sido objeto de considerable atención en la literatura de economía financiera en años recientes (ver, por ejemplo, Hardy, 2003).

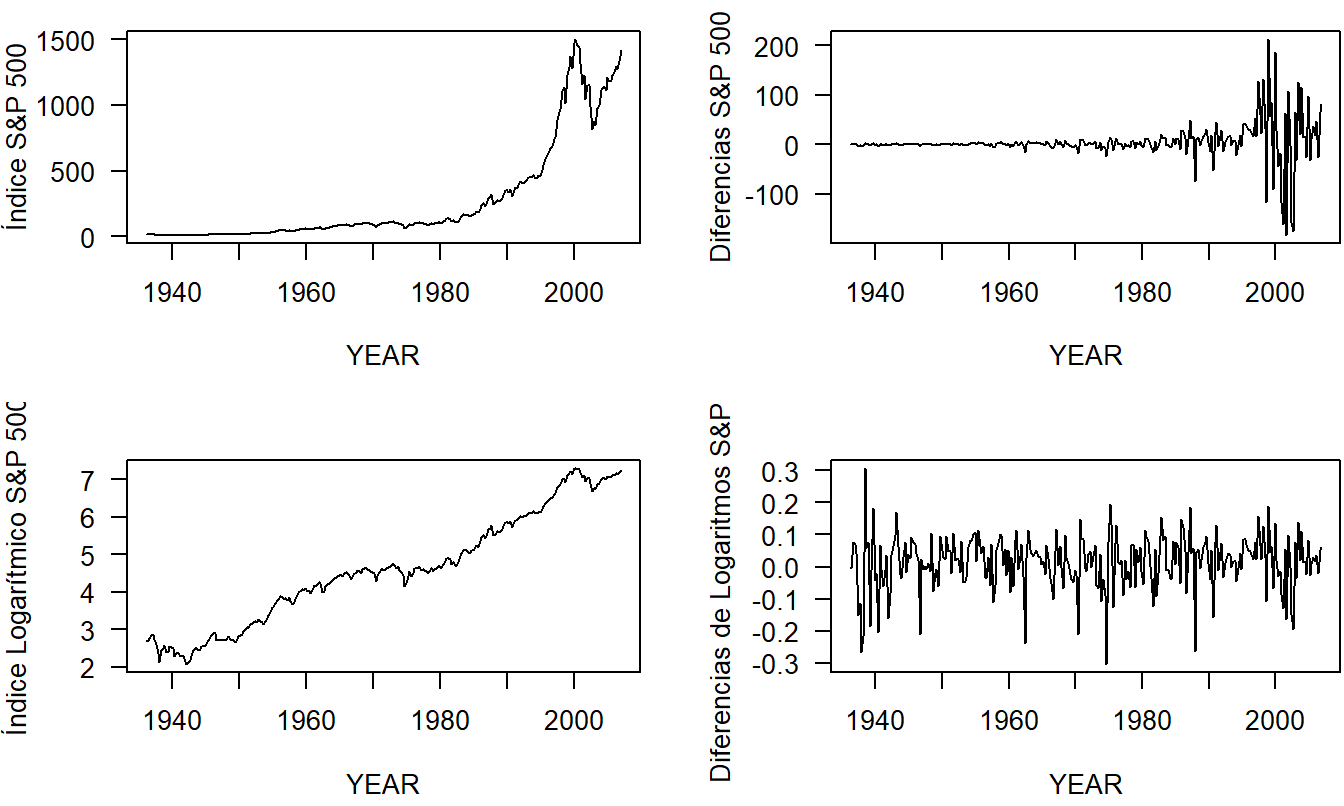
Gráficos de Series Temporales del Índice S & P 500. El panel superior izquierdo muestra la serie original que no es estacionaria en la media ni en la variabilidad. El panel superior derecho muestra las diferencias de la serie, que no son estacionarias en la variabilidad. El panel inferior izquierdo muestra el índice logarítmico, que no es estacionario en la media. El panel inferior derecho muestra las diferencias del índice logarítmico, que parecen ser estacionarias en la media y en la variabilidad.

Figura 7.9: Gráficos de Series Temporales del Índice S & P 500. El panel superior izquierdo muestra la serie original que no es estacionaria en la media ni en la variabilidad. El panel superior derecho muestra las diferencias de la serie, que no son estacionarias en la variabilidad. El panel inferior izquierdo muestra el índice logarítmico, que no es estacionario en la media. El panel inferior derecho muestra las diferencias del índice logarítmico, que parecen ser estacionarias en la media y en la variabilidad.

Código R para producir la Figura 7.9

7.6 Evaluación de Pronósticos

Evaluar la precisión de los pronósticos es importante al modelar datos de series temporales. En esta sección, presentamos técnicas de evaluación de pronósticos que:

  • Ayudan a detectar tendencias o patrones recientes no anticipados en los datos.
  • Son útiles para comparar diferentes métodos de pronóstico.
  • Proporcionan un método intuitivo y fácil de explicar para evaluar la precisión de los pronósticos.

En las primeras cinco secciones del Capítulo 7, presentamos varias técnicas para detectar patrones en los residuales de un modelo ajustado. Las medidas que resumen la distribución de los residuales se denominan estadísticas de bondad de ajuste. Como vimos en nuestro estudio de modelos transversales, al ajustar varios modelos diferentes a un conjunto de datos, introducimos la posibilidad de sobreajustar los datos. Para abordar esta preocupación, utilizaremos técnicas de validación fuera de muestra, similares a las introducidas en la Sección 6.5.

Para realizar una validación fuera de muestra de un modelo propuesto, idealmente se desarrollaría el modelo en un conjunto de datos y luego se corroboraría la utilidad del modelo en un segundo conjunto de datos independiente. Debido a que rara vez están disponibles dos conjuntos de datos ideales, en la práctica podemos dividir un conjunto de datos en dos submuestras: una submuestra de desarrollo del modelo y una submuestra de validación. Para datos longitudinales, la práctica consiste en utilizar la primera parte de la serie, las primeras \(T_1\) observaciones, para desarrollar uno o más modelos candidatos. La parte posterior de la serie, las últimas \(T_2=T-T_1\) observaciones, se utiliza para evaluar los pronósticos. Por ejemplo, podríamos tener diez años de datos mensuales, de modo que \(T=120\). Sería razonable utilizar los primeros ocho años de datos para desarrollar un modelo y los últimos dos años de datos para validación, obteniendo \(T_1=96\) y \(T_2=24\).

Por lo tanto, las observaciones \(y_1,\ldots , y_{T_1}\) se utilizan para desarrollar un modelo. A partir de estas \(T_1\) observaciones, podemos determinar los parámetros del modelo candidato. Usando el modelo ajustado, podemos determinar los valores ajustados para la submuestra de validación del modelo para \(t = T_1 + 1,T_1+2, \ldots, T_1+T_2\). Al tomar la diferencia entre los valores reales y los ajustados, obtenemos los residuales de pronósticos a un paso, denotados por \(e_t=y_t-\widehat{y}_t\). Estos residuales de pronóstico son las cantidades básicas que utilizaremos para evaluar y comparar técnicas de pronóstico.

Para comparar modelos, utilizamos un proceso de cuatro pasos similar al descrito en la Sección 6.5, descrito a continuación.

Proceso de Validación Fuera de Muestra

  1. Divide la muestra de tamaño \(T\) en dos submuestras: una submuestra de desarrollo del modelo (\(t=1,\ldots,T_1\)) y una submuestra de validación del modelo (\(t=T_1+1, \ldots, T_1 + T_2\)).
  2. Utilizando la submuestra de desarrollo del modelo, ajusta un modelo candidato al conjunto de datos \(t=1,\ldots,T_1\).
  3. Usando el modelo creado en el Paso 2 y las variables dependientes hasta e incluyendo \(t-1\), pronostica la variable dependiente \(\widehat{y}_t\), donde \(t=T_1+1, \ldots, T_1+T_2\).
  4. Utiliza las observaciones reales y los valores ajustados calculados en el Paso 3 para calcular los residuales de pronóstico a un paso, \(e_t = y_t- \widehat{y}_t\), para la submuestra de validación del modelo. Resume estos residuales con una o más estadísticas de comparación, descritas a continuación.

Repite los Pasos 2 al 4 para cada uno de los modelos candidatos. Elige el modelo con el menor conjunto de estadísticas de comparación.

La validación fuera de muestra se puede utilizar para comparar la precisión de los pronósticos de prácticamente cualquier modelo de pronóstico. Como vimos en la Sección 6.5, no estamos limitados a comparaciones donde un modelo es un subconjunto de otro, donde los modelos competidores usan las mismas unidades para la respuesta, y así sucesivamente.

Hay varias estadísticas que se utilizan comúnmente para comparar pronósticos.

Estadísticas Comúnmente Usadas para Comparar Pronósticos

  1. La estadística de error medio, definida por \[ ME=\frac{1}{T_2}\sum_{t=T_1+1}^{T_1+T_2}e_t. \] Esta estadística mide tendencias recientes no anticipadas por el modelo.

  2. El error porcentual medio, definido por \[ MPE=\frac{100}{T_2}\sum_{t=T_1+1}^{T_1+T_2}\frac{e_t}{y_t}. \] Esta estadística también mide tendencias, pero examina el error relativo al valor real.

  3. El error cuadrático medio, definido por \[ MSE=\frac{1}{T_2}\sum_{t=T_1+1}^{T_1+T_2}e_t^2. \] Esta estadística puede detectar más patrones que \(ME\). Es la misma que la estadística transversal \(SSPE\), excepto por la división por \(T_2\).

  4. El error absoluto medio, definido por \[ MAE=\frac{1}{T_2}\sum_{t=T_1+1}^{T_1+T_2}|e_t|. \] Al igual que \(MSE\), esta estadística puede detectar más patrones de tendencia que \(ME\). Las unidades de \(MAE\) son las mismas que la variable dependiente.

  5. El error absoluto porcentual medio, definido por \[ MAPE=\frac{100}{T_2}\sum_{t=T_1+1}^{T_1+T_2}|\frac{e_t}{y_t}|. \] Al igual que \(MAE\), esta estadística puede detectar más que patrones de tendencia. Al igual que \(MPE\), examina el error relativo al valor real.

Ejemplo: Tasas de Participación en la Fuerza Laboral - Continuación. Podemos utilizar medidas de validación fuera de muestra para comparar dos modelos para las \(LFPR\)s; el modelo de tendencia lineal en el tiempo y el modelo de paseo aleatorio. Para esta ilustración, examinamos las tasas de participación laboral para los años 1968 a 1994, inclusive. Esto corresponde a \(T_1 = 27\) observaciones definidas en el Paso 1. Posteriormente, se recopilaron datos de tasas para los años 1995 a 1998, inclusive, correspondientes a \(T_2 = 4\) para la validación fuera de muestra. Para el Paso 2, ajustamos cada modelo usando \(t=1,\ldots,27\), como se mostró anteriormente en este capítulo. Para el Paso 3, los pronósticos a un paso son:

\[ \widehat{y}_t = 0.2574 + 0.0145t \] y \[ \widehat{y}_t = y_{t-1} + 0.0132 \] para los modelos de tendencia lineal en el tiempo y de paseo aleatorio, respectivamente. Para el Paso 4, Tabla 7.2 resume las estadísticas de comparación de pronósticos. Basándonos en estas estadísticas, la elección del modelo es claramente el paseo aleatorio.

Tabla 7.2. Comparación de Pronósticos Fuera de Muestra

\[ \small{ \begin{array}{l|ccccc} \hline & ME & MPE & MSE & MAE & MAPE \\ \hline \text{Modelo de tendencia lineal en el tiempo} & -0.049 & -7.657 & 0.003 & 0.049 & 7.657 \\ \text{Modelo de paseo aleatorio} & -0.019 & -2.946 & 0.001 & 0.019 & 3.049 \\ \hline \end{array} } \]

Código R para producir la Tabla 7.2

7.7 Lecturas Adicionales y Referencias

Durante muchos años, los actuarios en América del Norte fueron introducidos al análisis de series temporales a través de Miller y Wichern (1977), Abraham y Ledolter (1983) y Pindyck y Rubinfeld (1991). Una introducción más reciente es Diebold (2004), que contiene una breve introducción a los modelos de cambio de régimen.

Debido a las dificultades relacionadas con su especificación y su uso limitado en pronósticos, no exploramos más los modelos causales en este texto. Para más detalles sobre los modelos causales, el lector interesado puede consultar Pindyck y Rubinfeld (1991).

Referencias del Capítulo

  • “Report of the Maturity Guarantees Working Party” (1980). Journal of the Institute of Actuaries 107, pp. 103-213.
  • Abraham, Bovas and Johannes Ledolter (1983). Statistical Methods for Forecasting. John Wiley & Sons, New York.
  • Diebold, Francis X. (2004). Elements of Forecasting, Third Edition. Thompson South-Western, Mason, OH.
  • Frees, Edward W. (2006). Forecasting of labor force participation rates. The Journal of Official Statistics 22(3), 453-485.
  • Fullerton, Howard N., Jr. (1999). Labor force projections to 2008: steady growth and changing composition. Monthly Labor Review, November, pp. 19-32.
  • Granger, Clive W. J and P. Newbold (1974). Spurious regressions in econometrics. Journal of Econometrics 2, 111-120.
  • Hardy, Mary (2001). A regime-switching model of long-term stock returns. North American Actuarial Journal 5(2), 41-53.
  • Hardy, Mary (2003). Investment Guarantees: Modeling and Risk Management for Equity-Linked Life Insurance. John Wiley & Sons, New York.
  • Miller, Robert B. and Dean W. Wichern (1977). Intermediate Business Statistics: Analysis of Variance, Regression and Time Series. Holt, Rinehart and Winston, New York.
  • Pindyck, R.S. and D.L. Rubinfeld (1991). Econometric Models and Economic Forecasts, Third Edition, McGraw-Hill, New York.

7.8 Ejercicios

7.1. Considera un paseo aleatorio \(\{y_t \}\) como la suma parcial de un proceso de ruido blanco \(\{ c_t \}\) con media \(\mathrm{E}~c_t= \mu_c\) y varianza \(\mathrm{Var}~c_t = \sigma_c^2\). Usa la ecuación (7.7) para demostrar:

  1. \(\mathrm{E}~y_t= y_0 + t \mu_c\), donde \(y_0\) es el valor inicial y

  2. \(\mathrm{Var}~y_t= t \sigma_c^2\).

7.2. Considera un paseo aleatorio \(\{y_t \}\) como la suma parcial de un proceso de ruido blanco \(\{ c_t \}\).

  1. Demuestra que el error de pronóstico a \(l\) pasos es \(y_{T+l}-\widehat{y_{T+l}} = \sum_{j=1}^l (c_{T+j} - \bar{c} ).\)

  2. Demuestra que la varianza aproximada del error de pronóstico a \(l\) pasos es \(l \sigma_c^2.\)

7.3. Tasas de Cambio del Euro. La tasa de cambio que consideramos es la cantidad de euros que se puede adquirir con un dólar estadounidense. Tenemos \(T=699\) observaciones diarias del periodo del 1 de abril de 2005 al 8 de enero de 2008. Estos datos fueron obtenidos de la Reserva Federal (informe H10). Fuente: Banco de la Reserva Federal de Nueva York. Nota: Los datos se basan en tasas de compra al mediodía en Nueva York de una muestra de participantes del mercado y representan tasas establecidas para transferencias cablegráficas pagaderas en las monedas indicadas. Estas son también las tasas de cambio requeridas por la Comisión de Valores de Estados Unidos para el sistema de divulgación integrado para emisores privados extranjeros.

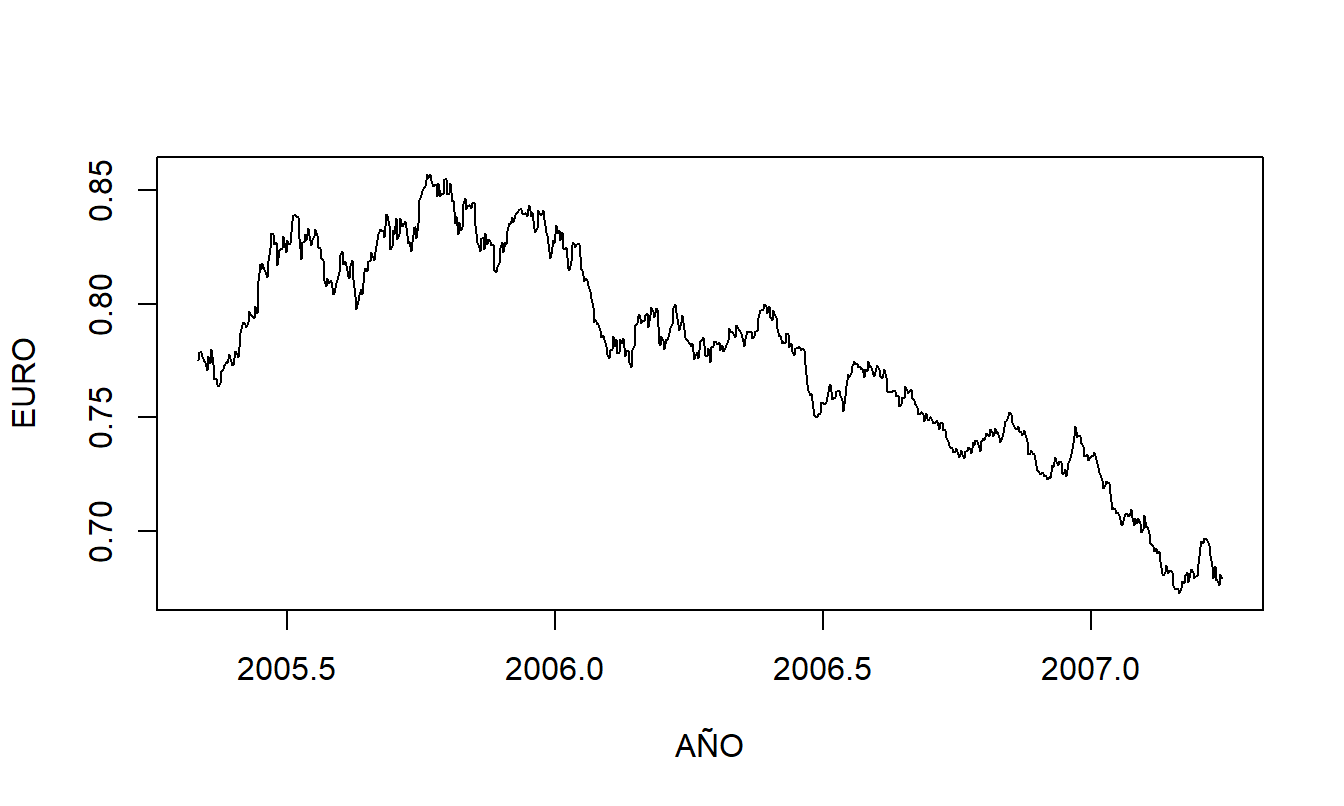
Gráfico de series temporales de la tasa de cambio del euro.

Figura 7.10: Gráfico de series temporales de la tasa de cambio del euro.

  1. La Figura 7.10 es un gráfico de series temporales de la tasa de cambio del euro.

a(i). Define el concepto de una serie temporal estacionaria.

a(ii). ¿Es la serie EURO estacionaria? Usa tu definición en la parte a(i) para justificar tu respuesta.

  1. Basándote en la inspección de la Figura 7.10 en la parte (a), decides ajustar un modelo de tendencia cuadrática a los datos. La Figura 7.11 superpone los valores ajustados en un gráfico de la serie.

b(i). Menciona varias estadísticas básicas de regresión que resumen la calidad del ajuste.

b(ii). Describe brevemente cualquier patrón de residuales que observes en la Figura 7.11.

b(iii). Aquí, el TIEMPO varía de \(1, 2, \ldots, 699\). Usando este modelo, calcula el pronóstico a tres pasos correspondiente a TIEMPO = 702.

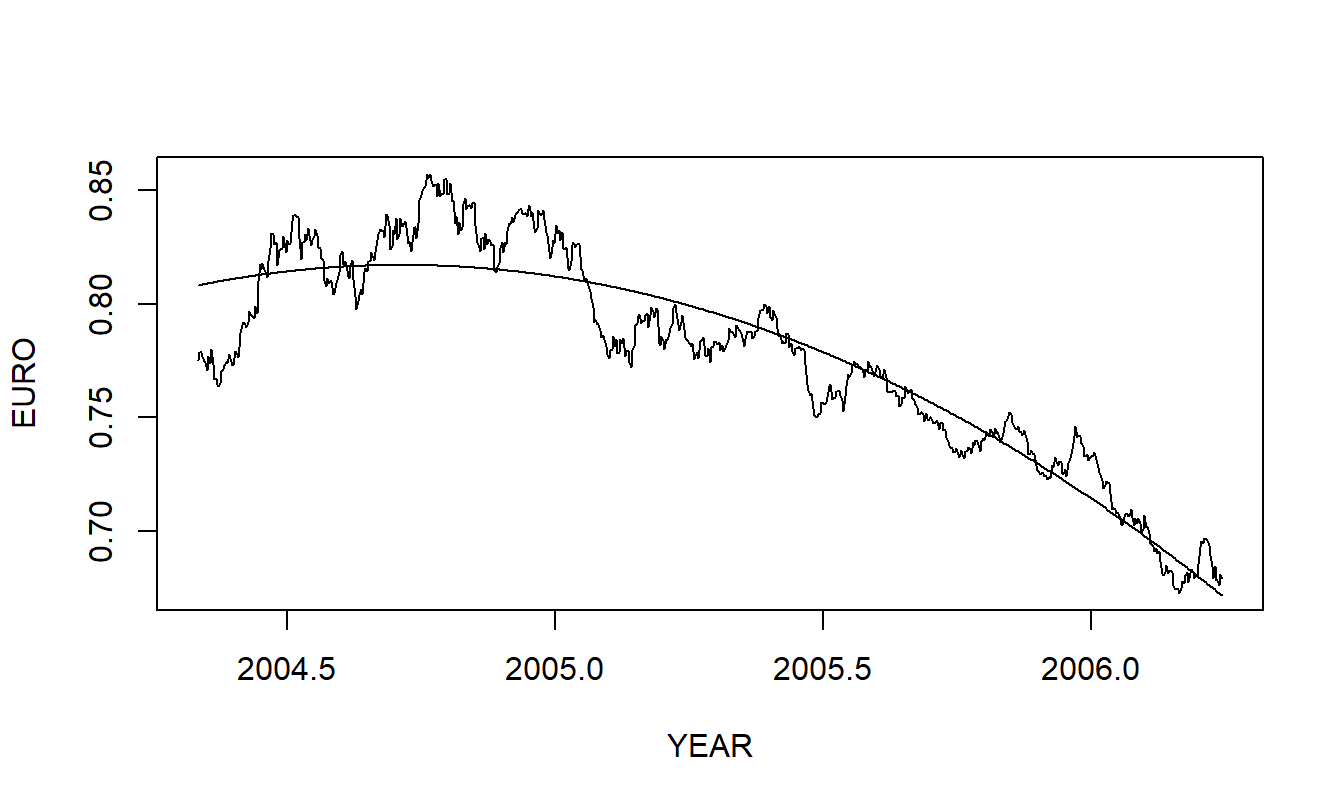
Curva ajustada cuadrática superpuesta en la tasa de cambio del euro.

Figura 7.11: Curva ajustada cuadrática superpuesta en la tasa de cambio del euro.

  1. Para investigar un enfoque diferente, DIFFEURO, calcula la diferencia de EURO. Decides modelar DIFFEURO como un proceso de ruido blanco.

c(i). ¿Cuál es el nombre del modelo correspondiente para EURO?

c(ii). El valor más reciente de EURO es \(EURO_{699} = 0.6795\). Usando el modelo identificado en la parte c(i), proporciona un pronóstico a tres pasos correspondiente a TIEMPO = 702.

c(iii). Usando el modelo identificado en la parte c(i) y el pronóstico puntual en la parte c(ii), proporciona el intervalo de predicción al 95% correspondiente para \(EURO_{702}\).