Capítulo 18 Credibilidad y Bonus-Malus
Vista previa del capítulo. Este capítulo introduce aplicaciones de regresión para la fijación de precios en los sistemas de experiencia de credibilidad y bonus-malus. Los sistemas de experiencia son métodos formales para incluir la experiencia de reclamos en las primas de renovación de contratos a corto plazo, como los de automóvil, salud y compensación laboral. Este capítulo proporciona breves introducciones a la credibilidad y el bonus-malus, enfatizando su relación con los métodos de regresión.
18.1 Clasificación de Riesgos y Experiencia
La clasificación de riesgos es un ingrediente clave en la fijación de precios de seguros. Las aseguradoras venden cobertura a precios que son suficientes para cubrir los reclamos anticipados, los gastos administrativos y un beneficio esperado para compensar el costo del capital necesario para respaldar la venta de la cobertura. En muchos países y líneas de negocio, el mercado de seguros es maduro y altamente competitivo. Esta fuerte competencia induce a las aseguradoras a clasificar los riesgos que suscriben con el fin de recibir primas justas por el riesgo asumido. Esta clasificación se basa en características conocidas del asegurado, la persona o empresa que busca la cobertura de seguro.
Por ejemplo, suponga que trabaja para una compañía que asegura pequeñas empresas por el tiempo perdido debido a empleados lesionados en el trabajo. Considere fijar el precio de este producto de seguro para dos empresas que son idénticas en cuanto al número de empleados, ubicación, distribución por edad y género, y así sucesivamente, excepto que una empresa es una firma de consultoría de gestión y la otra es una empresa de construcción. Basado en la experiencia, usted espera que la firma de consultoría tenga un nivel de reclamos menor que la empresa de construcción y necesita fijar precios en consecuencia. Si no lo hace, otra compañía de seguros ofrecerá un precio más bajo a la firma de consultoría y atraerá a este cliente potencial, dejando a su empresa solo con el negocio más costoso de la construcción.
La competencia entre aseguradoras conduce a cobrar primas según características observables, conocidas como clasificación de riesgos. En el contexto del modelado de regresión, esto puede considerarse como modelar las distribuciones de reclamos en términos de variables explicativas.
Muchas situaciones de fijación de precios se basan en una relación entre el asegurador y el asegurado que se desarrolla con el tiempo. Estas relaciones permiten a las aseguradoras basar los precios en características no observables del asegurado teniendo en cuenta la experiencia previa de reclamos del asegurado. Modificar las primas con el historial de reclamos se conoce como experiencia, a veces también llamada calificación por méritos.
Los métodos de experiencia se aplican de manera retrospectiva o prospectiva. Con métodos retrospectivos, se proporciona un “reembolso” de una parte de la prima al asegurado en caso de experiencia favorable (para el asegurador). Las primas retrospectivas son comunes en arreglos de seguros de vida (donde los asegurados ganan “dividendos” en los EE.UU. y “bonificaciones” en el Reino Unido). En seguros de bienes y accidentes, los métodos prospectivos son más comunes, donde la experiencia favorable del asegurado se “recompensa” a través de una prima de renovación más baja.
En este capítulo, discutimos dos métodos prospectivos que son adecuados para el modelado de regresión, la credibilidad y el bonus-malus. Los métodos de bonus-malus se usan ampliamente en Asia y Europa, aunque casi exclusivamente en seguros de automóviles. Como veremos en la Sección 18.4, la idea es usar la experiencia de reclamos para modificar la clasificación de un asegurado. Los métodos de credibilidad, introducidos en la Sección 18.2, se aplican más ampliamente en términos de líneas de negocio y geografía.
18.2 Credibilidad
La credibilidad es una técnica para fijar precios de coberturas de seguro que es ampliamente utilizada por actuarios en salud, seguros de vida colectivos y seguros de bienes y accidentes. En los Estados Unidos, los estándares se describen bajo el Actuarial Standard of Practice Number 25 publicado por la Actuarial Standards Board de la American Academy of Actuaries (sitio web: http://www.actuary.org/). Además, varias leyes y regulaciones de seguros requieren el uso de credibilidad.
La teoría de la credibilidad ha sido llamada un “pilar fundamental” del campo de la ciencia actuarial (Hickman y Heacox, 1999). La idea básica es usar la experiencia de reclamos y la información adicional para desarrollar una fórmula de precios, como a través de la relación \[\begin{equation} Nueva~Prima = \zeta \times Experiencia~de~Reclamos + (1 - \zeta) \times Prima~Anterior. \tag{18.1} \end{equation}\] Aquí, \(\zeta\) (la letra griega “zeta”) se conoce como el “factor de credibilidad;” los valores generalmente se encuentran entre cero y uno. El caso \(\zeta=1\) se conoce como “credibilidad total,” donde solo se utiliza la experiencia de reclamos para determinar la prima. El caso \(\zeta=0\) puede considerarse como “sin credibilidad,” donde se ignora la experiencia de reclamos y se utiliza información externa como la única base para fijar precios.
Para que este capítulo sea autosuficiente, comenzamos introduciendo algunos conceptos básicos de credibilidad. La Sección 18.2.1 revisa los conceptos clásicos de credibilidad, incluyendo cuándo usarla y las fórmulas de precios lineales. La Sección 18.2.2 describe la versión moderna de la credibilidad introduciendo un modelo probabilístico formal que puede usarse para actualizar los precios de los seguros. La Sección 18.3 discute el vínculo con el modelado de regresión.
18.2.1 Credibilidad de Fluctuación Limitada
La credibilidad tiene una larga historia en la ciencia actuarial, con contribuciones fundamentales que se remontan a Mowbray (1914). Posteriormente, Whitney (1918) introdujo el concepto intuitivamente atractivo de usar un promedio ponderado de (1) reclamos de la clase de riesgo y (2) reclamos de todas las clases de riesgo para predecir los reclamos esperados futuros.
Estándares para la Credibilidad Completa
El título del artículo de Mowbray fue “¿Qué tan extenso debe ser un historial de exposición a la nómina para obtener una prima pura confiable?” Sigue siendo la primera pregunta que un analista debe enfrentar: ¿cuándo necesito usar estimadores de credibilidad? Para comprender mejor esta pregunta, considere la siguiente situación.
Ejemplo: Costos Dentales. Suponga que está fijando el precio de la cobertura de seguro dental para un pequeño empleador. Para hombres de entre 18 y 25 años, el empleador proporciona la siguiente experiencia:
\[ \small{ \begin{array}{l|rrr} \hline \text{Año} & 2007 & 2008 & 2009 \\ \hline \text{Número} & 8 & 12 & 10 \\ \text{Costo Dental Promedio} & 500 & 400 & 900 \\ \hline \end{array} } \]
La “tarifa manual,” disponible a partir de una tabulación de un conjunto de datos mucho mayor, es $700 por empleado. Ignorando la inflación y los gastos, ¿qué usaría para anticipar los costos dentales en 2010? ¿La tarifa manual? ¿El promedio de los datos disponibles? ¿O alguna combinación?
Mowbray quería distinguir entre situaciones cuando (1) grandes empleadores con información sustancial podían usar su propia experiencia y (2) pequeños empleadores con experiencia limitada debían usar fuentes externas, conocidas como “tarifas manuales.” En terminología estadística, podemos pensar en formar un estimador de los costos medios verdaderos a partir de la experiencia de un empleador. Nos estamos preguntando si la distribución del estimador está lo suficientemente cerca de la media para ser confiable. Por supuesto, “suficientemente cerca” es la parte difícil, así que veamos una situación más concreta.
El conjunto más simple supone que tiene reclamos \(y_1, \ldots, y_n\) que son idénticamente e independientemente distribuidos (i.i.d.) con media \(\mu\) y varianza \(\sigma^2\). Como estándar para la credibilidad completa, podríamos requerir que \(n\) sea lo suficientemente grande para que
\[\begin{equation} \Pr ( (1-r) \mu \leq \bar{y} \leq (1+r) \mu) \geq p, \tag{18.2} \end{equation}\] donde \(r\) y \(p\) son constantes dadas. Por ejemplo, si \(r=0.05\) y \(p=0.9\), entonces deseamos tener al menos un 90% de probabilidad de estar dentro del 5% de la media.
Usando aproximaciones normales, es sencillo demostrar que es suficiente para la ecuación (18.2) que
\[\begin{equation} n \geq \left(\frac{\Phi^{-1}(\frac{p+1}{2}) \sigma}{r \mu} \right)^2 . \tag{18.3} \end{equation}\] Definimos \(n_F\), el número de observaciones requerido para la credibilidad completa, como el valor más pequeño de \(n\) que satisface la ecuación (18.3).
Ejemplo: Costos Dentales - Continuación. De la tabla, los costos promedio son \(\bar{y} = \left( 500 \times 8 + 400 \times 12 + 900 \times 10 \right)/30 = 593.33.\) Suponga que tenemos disponible una estimación de la desviación estándar \(\sigma \approx \widehat{\sigma}= 200.\) Usando \(p=0.90\), el percentil 90 de la distribución normal es \(\Phi^{-1}(.95) = 1.645\). Con \(r=0.05\), el tamaño de muestra aproximado requerido es \[ \left(\frac{\Phi^{-1}(.95) \widehat{\sigma}}{r \bar{y}} \right)^2 = \left(\frac{1.645 \times 200}{0.05 \times 593.33} \right)^2= 122.99, \] o \(n_F=123\). Basándonos en una muestra de tamaño 30, no tenemos suficientes observaciones para credibilidad completa.
Los estándares para credibilidad completa dados en las ecuaciones (18.2) y (18.3) se basan en la aproximación de normalidad. Es fácil construir reglas similares para otras distribuciones, como datos de conteo binomiales y de Poisson o combinaciones de distribuciones para pérdidas agregadas. Consulte Klugman, Panjer y Willmot (2008) para más detalles.
Credibilidad Parcial
Los actuarios no siempre trabajan con conjuntos de datos masivos. Puede que esté trabajando con la experiencia de un pequeño empleador o asociación y no tenga suficiente experiencia para cumplir con el estándar de credibilidad completa. O puede que esté trabajando con un gran empleador pero haya decidido descomponer sus datos en subconjuntos pequeños y homogéneos. Por ejemplo, si está trabajando con reclamos dentales, puede que desee crear varios grupos pequeños basados en la edad y el género.
Para grupos más pequeños que no cumplen con el umbral de credibilidad completa, Witney (1918) propuso usar un promedio ponderado entre la experiencia de reclamos del grupo y una tarifa manual. Suponiendo una aproximación de normalidad, la expresión para credibilidad parcial es \[\begin{equation} Nueva~Prima = Z \times \bar{y} + (1 - Z) \times Prima~Manual, \tag{18.4} \end{equation}\] donde \(Z\) es el “factor de credibilidad,” definido como \[\begin{equation} Z = \min{\LARGE\{}1,\sqrt{\frac{n}{n_F}} ~~{\LARGE\}}. \tag{18.5} \end{equation}\] Aquí, \(n\) es el tamaño de la muestra y \(n_F\) es el número de observaciones requerido para credibilidad completa.
Ejemplo: Costos Dentales - Continuación. Según el trabajo anterior, el estándar para credibilidad completa es \(n_F = 123\). Así, el factor de credibilidad es \(\min\{1,\sqrt{\frac{30}{123}} \} = 0.494.\) Con esto, la prima de credibilidad parcial es \[ Nueva~Prima = 0.494 \times 593.33 + (1 - 0.494) \times 700 = 647.31. \]
Una justificación para las fórmulas de credibilidad parcial en las ecuaciones (18.4) y (18.5) se presenta en los ejercicios. Según la ecuación (18.5), vemos que el factor de credibilidad \(Z\) está limitado entre 0 y 1; a medida que el tamaño de la muestra \(n\) y, por lo tanto, la experiencia aumentan, \(Z\) tiende a 1. Esto significa que los grupos más grandes son más “creíbles.” A medida que el factor de credibilidad \(Z\) aumenta, se le da mayor peso a la experiencia del grupo (\(\bar{y}\)). A medida que \(Z\) disminuye, se le da más peso a la prima manual, la tarifa que se desarrolla externamente basada en las características del grupo.
18.2.2 Credibilidad de Máxima Precisión
La teoría de la credibilidad fue utilizada durante más de cincuenta años en la fijación de precios de seguros antes de que se estableciera sobre una base matemática firme por Bühlmann (1967). Para introducir este marco, a veces conocido como “credibilidad de máxima precisión,” comencemos con la suposición de que tenemos una muestra de reclamos \(y_1, \ldots, y_n\) de un pequeño grupo y deseamos estimar la media para este grupo. Aunque el promedio muestral \(\bar{y}\) es ciertamente un estimador razonable, el tamaño de la muestra puede ser demasiado pequeño para depender exclusivamente de \(\bar{y}\). También suponemos que tenemos una estimación externa de la media general de reclamos, \(M\), que consideramos como una “prima manual.” La pregunta es si podemos combinar las dos estimaciones, \(\bar{y}\) y \(M\), para proporcionar un estimador que sea superior a cualquiera de las alternativas.
Bühlmann planteó la hipótesis de la existencia de características no observadas del grupo que denotamos como \(\alpha\); él se refirió a estas como “variables estructurales.” Aunque no observadas, estas características son comunes a todas las observaciones del grupo. Para reclamos dentales, las variables estructurales pueden incluir la calidad del agua donde se encuentra el grupo, el número de dentistas que proporcionan atención preventiva en el área, el nivel educativo del grupo, y otros factores. Por lo tanto, asumimos que, condicionado a \(\alpha\), \(\{y_1, \ldots, y_n\}\) son una muestra aleatoria de una población desconocida y, por ende, son i.i.d. Por notación, dejaremos que \(\mathrm{E}(y | \alpha)\) denote los reclamos esperados condicionales y \(\mathrm{Var}(y | \alpha)\) sea la varianza condicional correspondiente. Nuestro objetivo es determinar un “estimador” razonable de \(\mathrm{E}(y | \alpha)\).
Aunque no observadas, podemos aprender algo sobre las características \(\alpha\) a partir de observaciones repetidas de los reclamos. Para cada grupo, las funciones de media y varianza (condicionales) son \(\mathrm{E}(y | \alpha)\) y \(\mathrm{Var}(y | \alpha)\), respectivamente. La expectativa sobre todos los grupos de las funciones de varianza es E \(\mathrm{Var}(y | \alpha)\). De manera similar, la varianza de las expectativas condicionales es Var \(\mathrm{E}(y | \alpha)\).
Con estas cantidades en mano, podemos dar la prima de credibilidad de Bühlmann. \[\begin{equation} Nueva~Prima = \zeta \times \bar{y} + (1 - \zeta) \times M, \tag{18.6} \end{equation}\] donde \(\zeta\) es el “factor de credibilidad,” definido como \[\begin{equation} \zeta = \frac{n}{n+Ratio}, ~\mathrm{donde}~~~~~~~~Ratio = \frac{\mathrm{E~}\mathrm{Var}(y | \alpha)}{\mathrm{Var}~\mathrm{E}(y | \alpha)}. \tag{18.7} \end{equation}\] La fórmula de credibilidad en la ecuación (18.6) es la misma que la fórmula clásica de credibilidad parcial en la ecuación (18.4), con el factor de credibilidad \(\zeta\) en lugar de \(Z\). Por lo tanto, comparte la misma expresión intuitivamente agradable como un promedio ponderado. Además, ambos factores de credibilidad están en el intervalo \((0,1)\) y ambos aumentan hacia uno a medida que el tamaño de la muestra \(n\) aumenta.
Ejemplo: Costos Dentales - Continuación. A partir del trabajo anterior, sabemos que una estimación de la media condicional es 593.33. Use cálculos similares para mostrar que la varianza condicional estimada es 48,622.22.
Ahora supongamos que hay tres grupos adicionales con medias y varianzas condicionales dadas como sigue:
\[ \small{ \begin{array}{c|cccc} \hline & & \text{Media} & \text{Varianza} \\ & \text{Variable} & \text{Condicional} & \text{Condicional} & \text{Probabilidad} \\ \text{Grupo} & \text{No Observada} & \text{E} (y|\alpha) & \text{Var} (y|\alpha) & \Pr(\alpha) \\ \hline 1 & \alpha_1 & 593.33 & 48,622.22 & 0.20 \\ 2 & \alpha_2& 625.00 & 50,000.00 & 0.30 \\ 3 & \alpha_3& 800.00 & 70,000.00 & 0.25 \\ 4 & \alpha_4& 400.00 & 40,000.00 & 0.25 \\ \hline \end{array} } \] Suponemos que la probabilidad de pertenecer a un grupo está dada como \(\Pr(\alpha)\). Por ejemplo, esto puede determinarse tomando las proporciones del número de miembros en cada grupo.
Con esta información, es sencillo calcular la varianza condicional esperada, \[ \mathrm{E~}\mathrm{Var}(y | \alpha) = 0.2(48622.22) + 0.3(50000) + .25(70000) + .25(40000) = 52,224.44 . \]
Para calcular la varianza de las expectativas condicionales, se puede comenzar con la expectativa general \[ \mathrm{E~}\mathrm{E}(y | \alpha) = 0.2(593.33) + 0.3(625) + .25(800) + .25(400) = 606.166, \] y luego usar un procedimiento similar para calcular el valor esperado del segundo momento condicional, \(\mathrm{E~}(\mathrm{E}(y | \alpha))^2 = 387,595.6\). Con estas dos piezas, la varianza de las expectativas condicionales es \(\mathrm{E~}\mathrm{Var}(y | \alpha)\) \(= 387,595.6 - 606.166^2 = 20,158.\)
Esto produce el \(Ratio=52224.44/20158 = 2.591\) y, por lo tanto, el factor de credibilidad \(\zeta = \frac{30}{30+2.591} = 0.9205\). Con esto, la prima de credibilidad es \[ Nueva~Prima = 0.9205 \times 593.33 + (1 - 0.9205) \times 700 = 601.81. \]
Para ver cómo usar la fórmula de credibilidad con distribuciones alternativas, considere lo siguiente.
Ejemplo: Credibilidad con Datos de Conteo. Suponga que el número de reclamos cada año para un asegurado individual tiene una distribución de Poisson. La frecuencia de reclamos esperada anual de toda la población de asegurados está distribuida uniformemente en el intervalo (0,1). La frecuencia de reclamos esperada de un individuo es constante en el tiempo.
Considere un asegurado particular que tuvo 3 reclamos durante los tres años anteriores.
Bajo estas suposiciones, tenemos que los reclamos de un individuo \(y\) con características latentes \(\alpha\) tienen una distribución de Poisson con media condicional \(\alpha\) y varianza condicional \(\alpha\). La distribución de \(\alpha\) es uniforme en el intervalo (0,1), por lo que cálculos sencillos muestran que \[ \mathrm{E}~\mathrm{Var}(y|\alpha) = \mathrm{E}~\alpha = 0.5~~~\mathrm{y}~~~ \mathrm{Var}~\mathrm{E}(y|\alpha) = \mathrm{Var}~\alpha = 1/12 = 0.08333. \] Por lo tanto, con \(n=3\), el factor de credibilidad es \[ \zeta = \frac{3}{3+ 0.5/0.08333} = 0.3333. \] Con \(\bar{y}=3/3 =1\) y la media general \(\mathrm{E}~\mathrm{E}(y|\alpha)=0.5\) como la prima manual, la prima de credibilidad es \[ Nueva~Prima = 0.3333 \times 1 + (1 - 0.3333) \times 0.5 = 0.6667. \]
Más formalmente, la optimalidad del estimador de credibilidad se basa en lo siguiente.
Propiedad. Suponga que, condicionado a \(\alpha\), \(\{y_1, \ldots, y_n \}\) son idénticamente e independientemente distribuidos con media y varianza condicionales \(\mathrm{E}(y | \alpha)\) y \(\mathrm{Var}(y | \alpha)\), respectivamente. Suponga que deseamos estimar \(\mathrm{E}~(y_{n+1}|\alpha)\). Entonces, la prima de credibilidad dada en las ecuaciones (18.6) y (18.7) tiene la menor varianza dentro de la clase de todos los predictores lineales no sesgados.
Esta propiedad indica que la prima de credibilidad tiene la “máxima precisión” en el sentido de que tiene mínima varianza entre los predictores lineales no sesgados. Como hemos visto, está expresada en términos de medias y varianzas que pueden aplicarse a muchas distribuciones; a diferencia de la prima de credibilidad parcial, no hay suposición de normalidad. Es un resultado fundamental en el sentido de que se basa en observaciones (condicionalmente) i.i.d. No sorprendentemente, es fácil modificar este resultado básico para permitir diferentes exposiciones para las observaciones, tendencias en el tiempo, entre otros.
La propiedad no especifica cómo se estimarían las cantidades asociadas con la distribución de \(\alpha\). Para hacerlo, introduciremos un esquema de muestreo más detallado que nos permitirá incorporar métodos de regresión. Aunque no es la única forma de muestreo, este marco nos permitirá introducir muchas variaciones de interés y ayudará a interpretar la credibilidad de manera natural.
18.3 Credibilidad y Regresión
Al expresar la credibilidad en el marco de modelos de regresión, los actuarios pueden obtener varios beneficios:
- Los modelos de regresión ofrecen una amplia variedad de modelos entre los cuales elegir.
- El software estadístico estándar facilita el análisis de datos.
- Los actuarios tienen otro método para explicar el proceso de fijación de tarifas.
- Los actuarios pueden utilizar herramientas gráficas y de diagnóstico para seleccionar un modelo y evaluar su utilidad.
18.3.1 Modelo de Efectos Aleatorios Unidireccional
Supongamos que estamos interesados en fijar precios para \(n\) grupos y que para cada uno de los grupos \(i=1,\ldots,n\), tenemos experiencia de reclamos \(y_{it}, t=1, \ldots, T\). Aunque esta configuración de datos longitudinales se introdujo en el Capítulo 10, no necesitamos asumir que los reclamos evolucionan con el tiempo; los subíndices \(t\) pueden representar diferentes miembros de un grupo. Para comenzar, suponemos que no tenemos variables explicativas. La experiencia de reclamos sigue \[\begin{equation} y_{it} = \mu + \alpha_i + \varepsilon_{it}, ~~~~~ t=1, \ldots, T, i=1,\ldots, n, \tag{18.8} \end{equation}\] donde \(\mu\) representa un promedio general de reclamos, \(\alpha_i\) las características no observadas del grupo y \(\varepsilon_{it}\) la variación individual de los reclamos. Suponemos que \(\{\alpha_i\}\) son i.i.d. con media cero y varianza \(\sigma^2_{\alpha}\). Además, asumimos que \(\{\varepsilon_{it}\}\) son i.i.d. con media cero y varianza \(\sigma^2\) y son independientes de \(\alpha_i\). Estas son las suposiciones de un modelo básico de “efectos aleatorios unidireccional” descrito en la Sección 10.5.
Parece razonable usar la cantidad \(\mu + \alpha_i\) para predecir un nuevo reclamo del grupo \(i\)-ésimo. Para el modelo en la ecuación (18.8), parece intuitivamente plausible que \(\bar{y}\) sea un estimador deseable de \(\mu\) y que \(\bar{y}_i-\bar{y}\) sea un “estimador” deseable de \(\alpha_i\). Así, \(\bar{y}_i\) es un predictor deseable de \(\mu+\alpha_i\). Más generalmente, considere predictores de \(\mu+\alpha_i\) que sean combinaciones lineales de \(\bar{y}_i\) y \(\bar{y}\), es decir, \(c_1 \bar{y}_i+c_2\bar{y}\), para constantes \(c_1\) y \(c_2\). Para mantener la no sesgadez, usamos \(c_2 = 1 - c_1\). Algunos cálculos básicos muestran que el mejor valor de \(c_1\) que minimiza \(\mathrm{E} \left( c_1 \bar{y}_i+(1-c_1)\bar{y} - (\mu+\alpha_i) \right)^2\) es \[ c_1 = \frac{T}{T+\sigma^2/\sigma^2_{\alpha}} = \zeta, \] el factor de credibilidad. Esto produce el estimador de contracción, o predictor, de \(\mu+\alpha_i\), definido como \[\begin{equation} \bar{y}_{i,s} = \zeta \bar{y}_i+(1-\zeta)\bar{y}. \tag{18.9} \end{equation}\]
El estimador de contracción es equivalente a la prima de credibilidad cuando vemos que \[ \mathrm{Var} \left(\mathrm{E}(y_{it}|\alpha_i) \right) = \mathrm{Var} \left(\mathrm{E}(\mu+\alpha_i) \right) = \sigma^2_{\alpha} \] y \[ \mathrm{E} \left(\mathrm{Var}(y_{it}|\alpha_i) \right) = \mathrm{E} \left(\mathrm{E}(\sigma^2) \right) = \sigma^2 , \] por lo que \(Ratio = \sigma^2/\sigma^2_{\alpha}\). Así, el modelo de efectos aleatorios unidireccional a veces se conoce como el modelo “Bühlmann balanceado.” Este estimador de contracción también es un mejor predictor lineal no sesgado (\(BLUP\)), introducido en la Sección 15.1.3.
Ejemplo: Visualización de Contracción. Considere los siguientes datos ilustrativos:
\[ \small{ \begin{array}{c|cccc|c} \hline \text{Grupo}&&&&&\text{Promedio}\\ i& 1 & 2 & 3 & 4 & \text{del Grupo } (\bar{y}_i)\\ \hline 1 & 14 & 12 & 10 & 12 & 12 \\ 2 & 9 & 16 & 15 & 12 & 13 \\ 3 & 8 & 10 & 7 & 7 & 8 \\ \hline \end{array} } \]
Es decir, tenemos \(n=3\) grupos, cada uno con \(T=4\) observaciones. La media muestral es \(\bar{y} = 11\) y las medias muestrales específicas por grupo son \(\bar{y}_1=12\), \(\bar{y}_2=13\) y \(\bar{y}_3=8\). Ahora ajustamos el modelo ANOVA de efectos aleatorios unidireccional en la ecuación (18.8) utilizando la estimación de máxima verosimilitud, suponiendo normalidad. El software estadístico estándar muestra que las estimaciones de \(\sigma^2\) y \(\sigma^2_{\alpha}\) son 4.889 y 5.778, respectivamente. Esto implica que el factor \(\zeta\) estimado es 0.738. Usando la ecuación (18.9), las predicciones correspondientes para los grupos son 11.738, 12.476 y 8.786, respectivamente.
La Figura 18.1 compara las medias específicas por grupo con las predicciones correspondientes. Aquí, observamos una menor dispersión en las predicciones en comparación con las medias específicas por grupo; la estimación de cada grupo se “contrae” hacia la media general, \(\bar{y}\). Estas son las mejores predicciones asumiendo que \(\alpha_i\) son aleatorias. En contraste, las medias específicas por grupo son las mejores predicciones asumiendo que \(\alpha_i\) son determinísticas. Así, este “efecto de contracción” es una consecuencia de la especificación de efectos aleatorios.
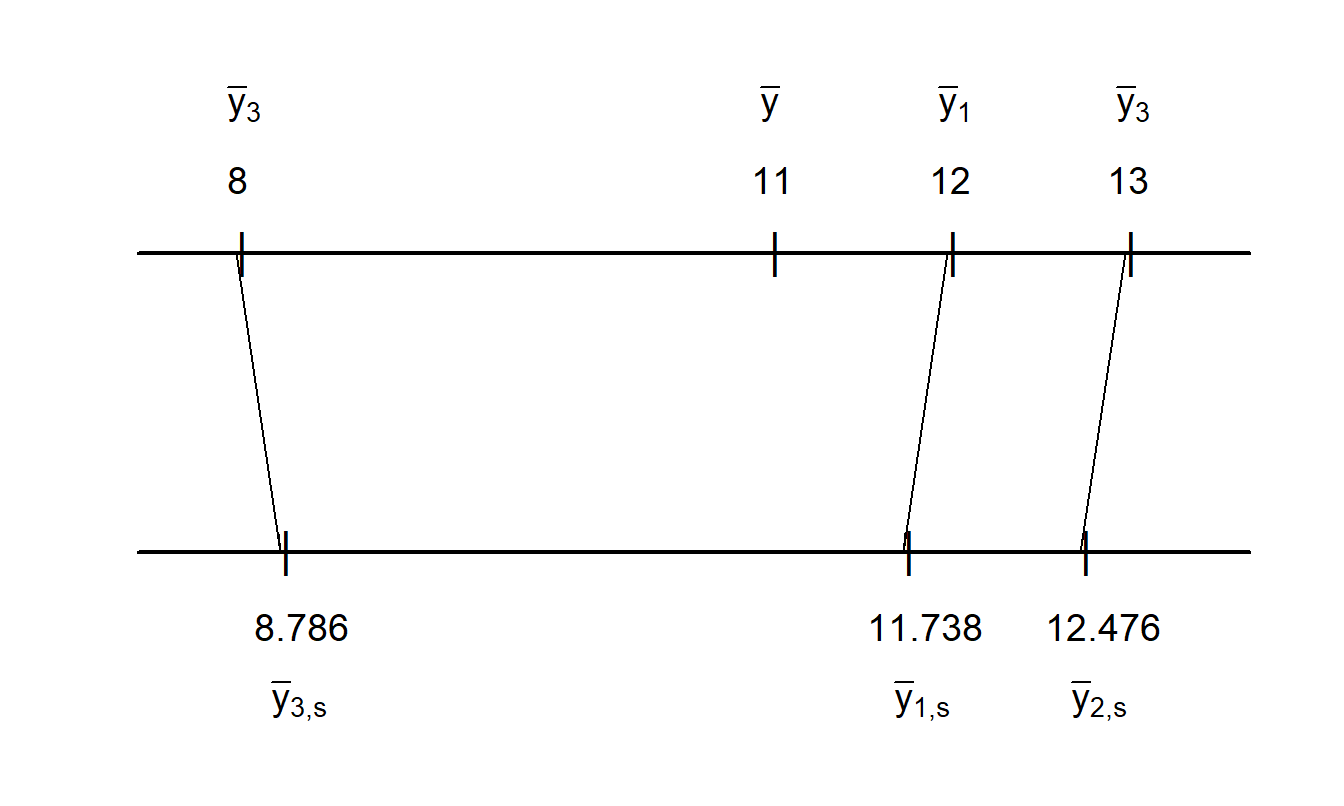
Figura 18.1: Comparación de las Medias Específicas por Grupo con las Estimaciones de Contracción. Para un conjunto de datos ilustrativo, las medias específicas por grupo y la media general se grafican en la escala superior. Las estimaciones de contracción correspondientes se grafican en la escala inferior. Esta figura muestra el aspecto de contracción de los modelos con efectos aleatorios.
Bajo el modelo de efectos aleatorios unidireccionales, tenemos que \(\bar{y}_i\) es un predictor no sesgado de \(\mu+\alpha_i\) en el sentido de que E (\(\bar{y}_i - (\mu+\alpha_i)\))=0. Sin embargo, \(\bar{y}_i\) es ineficiente en el sentido de que el estimador de contracción, \(\bar{y}_{i,s}\), tiene un error cuadrático medio menor que \(\bar{y}_i\). Intuitivamente, dado que \(\bar{y}_{i,s}\) es una combinación lineal de \(\bar{y}_i\) y \(\bar{y}\), decimos que ha sido “contraído” hacia el estimador \(\bar{y}\). Además, debido a la información adicional en \(\bar{y}_{i,s}\), es habitual interpretar un estimador de contracción como “tomar prestada fuerza” del estimador de la media general.
Tenga en cuenta que el estimador de contracción se reduce al estimador de efectos fijos \(\bar{y}_i\) cuando el factor de credibilidad, \(\zeta\), se convierte en 1. Es fácil ver que \(\zeta \rightarrow 1\) cuando (i) \(T\rightarrow\infty\) o (ii) \(\sigma^2/\sigma^2_{\alpha}\rightarrow 0\). Es decir, el mejor predictor se aproxima a la media del grupo cuando (i) el número de observaciones por grupo se vuelve grande o (ii) la variabilidad entre grupos se vuelve grande en relación con la variabilidad de la respuesta. En lenguaje actuarial, cualquiera de los casos respalda la idea de que la información del grupo \(i\) se está volviendo más “creíble.”
18.3.2 Modelos Longitudinales
Como hemos visto en el contexto del modelo de efectos aleatorios unidireccionales con replicaciones balanceadas, el estimador de credibilidad de máxima precisión de Bühlmann es equivalente al mejor predictor lineal no sesgado presentado en la Sección 15.1.3. Esto también es cierto al considerar una configuración de muestreo longitudinal más general introducida en el Capítulo 10 (ver, por ejemplo, Frees, Young y Luo, 1999). Al expresar el problema de credibilidad en términos de un esquema de muestreo basado en regresión, podemos usar técnicas de regresión bien conocidas para estimar parámetros y predecir cantidades desconocidas. Ahora consideramos un modelo longitudinal que aborda muchos casos especiales de interés en la práctica actuarial.
Supongamos que la experiencia de reclamos sigue \[\begin{equation} y_{it} = M_i + \mathbf{x}_{it}^{\prime} \boldsymbol \beta+ \mathbf{z}_{it}^{\prime} {\boldsymbol \alpha}_i + \varepsilon_{it},~~~~~ t=1, \ldots, T_i, i=1,\ldots, n. \tag{18.10} \end{equation}\] Consideremos cada componente del modelo por turno:
\(M_i\) representa la prima manual que se supone conocida. En el lenguaje de los modelos lineales generalizados, \(M_i\) es una “variable de ajuste.” Al estimar el modelo de regresión, simplemente se usa \(y_{it}^{\ast} = y_{it} - M_i\) como la variable dependiente. Si la prima manual no está disponible, entonces tome \(M_i = 0\).
\(\mathbf{x}_{it}^{\prime} \boldsymbol \beta\) es la combinación lineal usual de variables explicativas. Estas pueden usarse para ajustar la prima manual. Por ejemplo, puede tener una proporción mayor de lo típico de hombres (o mujeres) en su grupo y desear considerar el género de los miembros del grupo. Esto puede hacerse utilizando una variable binaria de género como predictor y pensando en el coeficiente de regresión como la cantidad para ajustar la prima manual. De manera similar, podría usar la edad, experiencia u otras características de los miembros del grupo para ajustar las primas manuales. Las variables explicativas también pueden describir al grupo, no solo a los miembros. Por ejemplo, puede desear incluir variables explicativas que proporcionen información sobre la ubicación del lugar de trabajo (como urbano versus rural) para ajustar las primas manuales.
\(\mathbf{z}_{it}^{\prime} {\boldsymbol \alpha}_i\) representa una combinación lineal de efectos aleatorios que puede escribirse como \(\mathbf{z}_{it}^{\prime} {\boldsymbol \alpha}_i = z_{it,1} \alpha_{i,1} + \cdots +z_{it,q} \alpha_{i,q}\). A menudo, solo hay un único intercepto aleatorio, de modo que \(q=1\), \(z_{it}=1\) y \(\mathbf{z}_{it}^{\prime} {\boldsymbol \alpha}_i = \alpha_{i1} = \alpha_i\). Los efectos aleatorios tienen media cero, pero una media no nula puede incorporarse usando \(\mathbf{x}_{it}^{\prime} \boldsymbol \beta\). Por ejemplo, podríamos usar el tiempo \(t\) como una variable explicativa y definir \(\mathbf{x}_{it}=\mathbf{z}_{it}=(1 ~t)^{\prime}\). Entonces, la ecuación (18.10) se reduce a \(y_{it} = \beta_0 + \alpha_{i1} + ( \beta_1 + \alpha_{i2}) \times t+ \varepsilon_{it}\), un modelo propuesto por Hachemeister en 1975.
\(\varepsilon_{it}\) es el término de perturbación con media cero. En muchas aplicaciones, se le asigna un peso en el sentido de que \(\mathrm{Var}~\varepsilon_{it} = \sigma^2 /w_{it}.\) Aquí, el peso \(w_{it}\) es conocido y representa una exposición, como la cantidad de prima de seguro, el número de empleados, el tamaño de la nómina, el número de vehículos asegurados, entre otros. Introducir pesos fue propuesto por Bühlmann y Straub en 1970. Los términos de perturbación típicamente se asumen independientes entre grupos (sobre \(i\)), pero en algunas aplicaciones, pueden incorporar patrones temporales, como \(AR\)(1) (autoregresivo de orden 1).
Ejemplo: Compensación de Trabajadores. Consideramos el seguro de compensación de trabajadores, examinando las pérdidas debido a reclamos por discapacidad parcial permanente. Los datos provienen de Klugman (1992), quien exploró representaciones del modelo bayesiano, y originalmente del National Council on Compensation Insurance. Consideramos \(n=121\) clases ocupacionales durante \(T=7\) años. Para proteger las fuentes de los datos, no se dispone de información adicional sobre las clases ocupacionales y los años. Resumimos el análisis en Frees, Young y Luo (2001).
La variable de respuesta de interés es la prima pura (PP), definida como las pérdidas por discapacidad parcial permanente por dólar de PAYROLL. La variable PP es de interés para los actuarios porque las tasas de compensación de trabajadores se determinan y cotizan por unidad de PAYROLL. La medida de exposición, PAYROLL, es una de las posibles variables explicativas. Otras variables explicativas son YEAR (= 1, , 7) y la clase ocupacional.
Entre otras representaciones, Frees et al. (2001) consideraron el modelo de Bühlmann-Straub, \[\begin{equation} \ln (PP)_{it} = \beta_0 + \alpha_{i1}+ \varepsilon_{it}, \tag{18.11} \end{equation}\] el modelo de Hachemeister \[\begin{equation} \ln (PP)_{it} = \beta_0 + \alpha_{i1} + (\beta_1+\alpha_{i2})YEAR_t + \varepsilon_{it}, \tag{18.12} \end{equation}\] y una versión intermedia \[\begin{equation} \ln (PP)_{it} = \beta_0 + \alpha_{i1}+ \alpha_{i2}YEAR_t + \varepsilon_{it}. \tag{18.13} \end{equation}\] En los tres casos, los pesos están dados por \(w_{it}= PAYROLL_{it}\). Estos modelos son todos casos especiales del modelo general en la ecuación (18.10) con \(y_{it} = \ln (PP)_{it}\) y \(M_i=0\).
La estimación de parámetros y la inferencia estadística relacionada, incluida la predicción, para el modelo de regresión lineal mixto en la ecuación (18.10) han sido ampliamente investigadas. La literatura se resume brevemente en la Sección 15.1. De la Sección 15.1.3, el mejor predictor lineal no sesgado de \(\mathrm{E}(y_{it} | \boldsymbol \alpha)\) tiene la forma \[\begin{equation} M_i + \mathbf{x}_{it}^{\prime} \mathbf{b}_{GLS}+ \mathbf{z}_{it}^{\prime} \mathbf{a}_{BLUP,i}, \tag{18.14} \end{equation}\] donde \(\mathbf{b}_{GLS}\) es el estimador de mínimos cuadrados generalizados de \(\boldsymbol \beta\) y la expresión general para \(\mathbf{a}_{BLUP,i}\) se da en la ecuación (15.11). Este es un estimador de credibilidad general que puede calcularse fácilmente utilizando paquetes estadísticos.
Caso Especial: Modelo de Bühlmann-Straub. Para el modelo de Bühlmann-Straub, el factor de credibilidad es \[ \zeta_{i,w} = \frac{WT_i}{WT_i + \sigma^2/\sigma^2_{\alpha}}, \] donde \(WT_i\) es la suma de pesos para el grupo \(i\)-ésimo, \(WT_i = \sum_{t=1}^{T_i} w_{it}\).
Usando la ecuación (18.14) en el modelo de Bühlmann-Straub, es fácil verificar que la predicción para el grupo \(i\)-ésimo es \[ \zeta_{i,w} \bar{y}_{i,w} + (1-\zeta_{i,w} ) \bar{y}_w , \] donde \[ \bar{y}_{i,w} =\frac{\sum_{t=1}^{T_i} w_{it}y_{it}}{WT_i} ~~~~\mathrm{y}~~~~~~\bar{y}_w =\frac{\sum_{t=1}^{T_i} \zeta_{i,w} \bar{y}_{i,w}}{\sum_{t=1}^{T_i} \zeta_{i,w} } \] son la media ponderada del grupo \(i\)-ésimo y la media ponderada general, respectivamente. Esto se reduce al predictor balanceado de Bühlmann al tomar pesos idénticos a 1. Consulte, por ejemplo, Frees (2004, Sección 4.7) para más detalles.
Ejemplo: Compensación de Trabajadores - Continuación. Estimamos los modelos en las ecuaciones (18.11)-(18.13), así como el modelo de Bühlmann no ponderado, utilizando máxima verosimilitud. Tabla 18.1 resume los resultados. Esta tabla sugiere que el factor de tendencia anual no es estadísticamente significativo, al menos para las medias condicionales. La tendencia anual que varía según la clase ocupacional parece ser útil. El criterio de información \(AIC\) sugiere que el modelo intermedio dado en la ecuación (18.13) proporciona el mejor ajuste a los datos.
Tabla 18.1. Ajustes del Modelo de Compensación de Trabajadores
\[ \small{ \begin{array}{l|rrrr}\hline & & \text{Bühlmann-Straub} & \text{Hachemeister} \\ \text{Parámetro} & \text{Bühlmann} & Eq (18.11) &Eq (18.12) & Eq (18.13) \\ \hline \beta_0 & -4.3665 & -4.4003& -4.3805& -4.4036 \\ (t-\text{estadístico}) & (-50.38)& (-51.47) & (-44.38)& (-51.90) \\ \beta_1 & & & -0.00446& \\ (t-\text{estadístico}) & & & (-0.47) \\ \hline \sigma_{\alpha,1} &0.9106 & 0.8865 & 0.9634 & 0.9594\\ \sigma_{\alpha,2} & & & 0.0452 & 0.0446\\ \sigma & 0.5871& 42.4379& 41.3386 & 41.3582\\\hline AIC & 1,715.924 & 1,571.391& 1,567.769&1,565.977 \\ \hline \end{array} } \]
Código R para Generar la Tabla 18.1
Tabla 18.2 ilustra las predicciones de credibilidad resultantes para las primeras cinco clases ocupacionales. Aquí, para cada método, después de realizar la predicción, se exponenció el resultado y se multiplicó por 100, de modo que estos son los centavos de pérdidas predichas por dólar de PAYROLL. También se incluyen las predicciones para el modelo de “efectos fijos”, que equivalen a tomar el promedio por clase ocupacional durante el período de siete años. Las predicciones para los modelos de Hachemeister y la ecuación (18.13) se realizaron para el Año 8.
Tabla 18.2 muestra un acuerdo sustancial entre las predicciones de Bühlmann y Bühlmann-Straub, lo que indica que la ponderación por PAYROLL es menos importante para este conjunto de datos. También hay un acuerdo sustancial entre las predicciones del modelo de Hachemeister y la ecuación (18.13), lo que indica que la tendencia temporal general es menos importante. Comparar los dos conjuntos de predicciones indica que una tendencia temporal que varía según la clase ocupacional sí marca una diferencia.
Tabla 18.2. Predicciones de Compensación de Trabajadores
\[ \small{ \begin{array}{c|rrrr}\hline \text{Clase} & \text{Efectos} & && & \\ \text{Ocupacional } & \text{Fijos} & \text{Bühlmann} & \text{Bühlmann-Straub} & \text{Hachemeister} & Eq (18.13) \\ \hline \hline 1 & 2.981 & 2.842 & 2.834 & 2.736 & 2.785 \\ 2 & 1.941 & 1.895 & 1.875 & 1.773 & 1.803 \\ 3 & 1.129 & 1.137 & 1.135 & 1.124 & 1.139 \\ 4 & 0.795 & 0.816 & 0.765 & 0.682 & 0.692 \\ 5 & 1.129 & 1.137 & 1.129 & 1.062 & 1.079 \\ \hline \end{array} } \]
18.4 Bonus-Malus
Los métodos bonus-malus de experiencia de clasificación se utilizan extensamente en la fijación de precios de seguros de automóviles en Europa y Asia. Para entender este tipo de clasificación por experiencia, primero consideremos precios basados en características observables. En el seguro de automóviles, estas incluyen características del conductor (como edad y género), características del vehículo (como tipo de coche y si se usa para trabajar o no) y características territoriales (como el condado de residencia). El uso exclusivo de estas características para los precios da como resultado una prima a priori. En los EE.UU. y Canadá, esta es la base principal de la prima; la clasificación por experiencia entra de forma limitada en forma de recargos por accidentes con culpa y violaciones de tránsito en movimiento.
Los sistemas bonus-malus (BMS) proporcionan una integración más detallada de la experiencia de reclamos en los precios. Típicamente, un BMS clasifica a los asegurados en una de varias categorías ordenadas. Un asegurado entra al sistema en una categoría específica. En el año siguiente, los asegurados sin accidentes reciben un “bono” y suben de categoría. Los asegurados que tienen accidentes con culpa durante el año reciben un “malus” y bajan un número especificado de categorías. La categoría en la que uno reside dicta el factor bonus-malus, o BMF. El BMF multiplicado por la prima a priori se conoce como la prima a posteriori.
Para ilustrar, Lemaire (1998) da un ejemplo de un sistema brasileño que se resume en la Tabla 18.3. En este sistema, uno comienza en la Clase 7, pagando el 100% de las primas dictadas por la prima a priori del asegurador. En el año siguiente, si el asegurado no tiene accidentes, paga solo el 90% de la prima a priori. De lo contrario, la prima es el 100% de la prima a priori.
Tabla 18.3. Sistema Bonus-Malus Brasileño
\[ \small{ \begin{array}{c|rrrrrrrr}\hline \hline & & &&\text{Clase}& \text{Después}\\ \text{Clase } & BMF & \text{Reclamos} & \text{Reclamos} & \text{Reclamos} & \text{Reclamos} & \text{Reclamos} & \text{Reclamos} & \text{Reclamos} \\ \text{Antes} & & 0 & 1 & 2 & 3 & 4 & 5 & \geq 6 \\ \hline 7 & 100 & 6 & 7 & 7 & 7 & 7 & 7 & 7 \\ 6 & 90 & 5 & 7 & 7 & 7 & 7 & 7 & 7 \\ 5 & 85 & 4 & 6 & 7 & 7 & 7 & 7 & 7 \\ 4 & 80 & 3 & 5 & 6 & 7 & 7 & 7 & 7 \\ 3 & 75 & 2 & 4 & 5 & 6 & 7 & 7 & 7 \\ 2 & 70 & 1 & 3 & 4 & 5 & 6 & 7 & 7 \\ 1 & 65 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline \end{array} } \] Fuente: Lemaire (1998)
Como se describe en Lemaire (1998), el sistema brasileño es simple en comparación con otros (el sistema belga tiene 23 clases). Las aseguradoras que operan en países con sistemas bonus-malus detallados no requieren extensas variables de calificación a priori en comparación con los EE.UU. y Canadá. Esto generalmente implica menores gastos de suscripción y, por lo tanto, un sistema de seguros menos costoso. Además, muchos argumentan que es más justo para los asegurados en el sentido de que aquellos con mala experiencia de reclamos soportan la carga de primas más altas y no se penaliza simplemente por género u otras variables de calificación que están fuera del control del asegurado. Consulte Lemaire (1995) para una amplia discusión sobre cuestiones institucionales, regulatorias y éticas relacionadas con los sistemas bonus-malus.
A lo largo de este libro, hemos visto cómo utilizar técnicas de regresión para calcular primas a priori. Dionne y Vanasse (1992) señalaron las ventajas de usar un marco de regresión para calcular factores bonus-malus. Esencialmente, usaron una variable latente para representar las tendencias no observadas de un asegurado para involucrarse en un accidente (agresividad, rapidez de reflejos) con modelos de conteo de regresión para calcular primas a posteriori. Consulte Denuit et al. (2007) para una visión general reciente de esta área en desarrollo.
Consulte Norberg (1986) para un relato temprano que relaciona la teoría de credibilidad con el marco de modelos lineales mixtos. El tratamiento aquí sigue a Frees, Young y Luo (1999).
Al demostrar que muchos modelos importantes de credibilidad pueden verse en un marco de datos longitudinales (lineal), limitamos nuestra consideración a ciertos tipos de modelos de credibilidad. Específicamente, los modelos de datos longitudinales acomodan solo riesgos no observados que son aditivos. Este capítulo no aborda modelos de efectos aleatorios no lineales que han sido investigados en la literatura actuarial; consulte, por ejemplo, Taylor (1977) y Norberg (1980). Taylor (1977) permitió que los reclamos de seguros fueran posiblemente de dimensión infinita usando la teoría de espacios de Hilbert y estableció fórmulas de credibilidad en este contexto general. Norberg (1980) consideró el contexto más concreto, pero aún general, de reclamos multivariantes y estableció la relación entre la credibilidad y la estimación estadística Bayes empírica. Como se describe en la Sección 18.4, Denuit et al. (2007) proporciona una visión general reciente de modelos de conteo de reclamos longitudinales no lineales.
Para considerar toda la distribución de reclamos, un enfoque común utilizado en credibilidad es adoptar una perspectiva bayesiana. Keffer (1929) inicialmente sugirió usar una perspectiva bayesiana para la calificación de experiencia en el contexto del seguro de vida grupal. Posteriormente, Bailey (1945, 1950) mostró cómo derivar la forma de credibilidad lineal desde una perspectiva bayesiana como la media de una distribución predictiva. Varios autores han proporcionado extensiones útiles de este paradigma. Jewell (1980) extendió los resultados de Bailey a una clase más amplia de distribuciones, la familia exponencial, con distribuciones previas conjugadas para las variables estructurales.
Referencias del Capítulo
- Bailey, Arthur (1945). A generalized theory of credibility. Proceedings of the Casualty Actuarial Society 32.
- Bailey, Arthur (1950). Credibility procedures: LaPlace’s generalization of Bayes’ rule and the combination of collateral knowledge with observed data. Proceedings of the Casualty Actuarial Society Society 37, 7-23.
- Bühlmann, Hans (1967). Experience rating and credibility. ASTIN Bulletin 4, 199-207.
- Bühlmann, Hans and E. Straub (1970). Glaubwürdigkeit für schadensätze. Mitteilungen der Vereinigung Schweizerischer Versicherungs-Mathematiker 70, 111-133.
- Dionne, George and C. Vanasse (1992). Automobile insurance ratemaking in the presence of asymmetrical information. Journal of Applied Econometrics 7, 149-165.
- Denuit, Michel, Xavier Marechal, Sandra Pitrebois and Jean-Francois Walhin (2007). Actuarial Modelling of Claim Counts: Risk Classification, Credibility and Bonus-Malus Systems. Wiley, New York.
- Frees, Edward W., Virginia R. Young, and Yu Luo (1999). A longitudinal data analysis interpretation of credibility models. Insurance: Mathematics and Economics 24, 229-247.
- Frees, Edward W., Virginia R. Young, and Yu Luo (2001). Case studies using panel data models. North American Actuarial Journal 5(4), 24-42.
- Frees, Edward W. (2004). Longitudinal and Panel Data: Analysis and Applications in the Social Sciences. Cambridge University Press, New York.
- Hachemeister, Charles A. (1975). Credibility for regression models with applications to trend. In Credibility: Theory and Applications, editor Paul M. Kahn. Academic Press, New York, 129-163.
- Keffer, R (1929). An experience rating formula. Transactions of the Actuarial Society of America 30, 130-139.
- Klugman, Stuart A. (1992). Bayesian Statistics in Actuarial Science. Kluwer, Boston.
- Klugman, Stuart A, Harry H. Panjer and Gordon E. Willmot (2008). Loss Models: From Data to Decisions. John Wiley & Sons, Hoboken, New Jersey.
- Lemaire, Jean (1995). Bonus-Malus Systems in Automobile Insurance. Kluwer, Boston.
- Lemaire, Jean (1998). Bonus-malus systems: The European and Asian approach to merit-rating. North American Actuarial Journal 2(1), 26-47.
- Mowbray, Albert H. (1914). How extensive a payroll exposure is necessary to give a dependable pure premium. Proceedings of the Casualty Actuarial Society 1, 24-30.
- Norberg, Ragnar (1980). Empirical Bayes credibility. Scandinavian Actuarial Journal 177-194.
- Norberg, Ragnar (1986). Hierarchical credibility: Analysis of a random effect linear model with nested classification. Scandinavian Actuarial Journal 204-22.
- Taylor, Greg C. (1977). Abstract credibility. Scandinavian Actuarial Journal 149-68.
- Whitney, Albert W. (1918). The theory of experience rating. Proceedings of the Casualty Actuarial Society 4.