Chapter 4 Regresión Lineal Múltiple - II

Vista previa del capítulo. Este capítulo amplía la discusión sobre la regresión lineal múltiple al introducir la inferencia estadística para manejar varios coeficientes simultáneamente. Para motivar esta extensión, este capítulo considera los coeficientes asociados con variables categóricas. Estas variables nos permiten agrupar observaciones en distintas categorías. Este capítulo muestra cómo incorporar variables categóricas en funciones de regresión utilizando variables binarias, ampliando así considerablemente el alcance de las posibles aplicaciones del análisis de regresión. La inferencia estadística para varios coeficientes permite a los analistas tomar decisiones sobre variables categóricas, así como otras aplicaciones importantes. Las variables explicativas categóricas también proporcionan la base para un modelo de ANOVA, un tipo especial de modelo de regresión que permite un análisis e interpretación más sencillos.

4.1 El Papel de las Variables Binarias

Las variables categóricas proporcionan etiquetas para observaciones, para denotar la pertenencia a grupos o categorías distintas. Una variable binaria es un caso especial de una variable categórica. Para ilustrar, una variable binaria puede indicarnos si alguien tiene o no seguro de salud. Una variable categórica podría indicarnos si alguien tiene:

• seguro privado grupal (ofrecido por empleadores y asociaciones),
• seguro privado individual (a través de compañías de seguros),
• seguro público (como Medicare o Medicaid),
• sin seguro de salud.

Para las variables categóricas, puede o no existir un orden de los grupos. En el caso del seguro de salud, es difícil ordenar estas cuatro categorías y decir cuál es “mayor”: seguro privado grupal, seguro privado individual, seguro público o sin seguro de salud. En contraste, para la educación, podríamos agrupar a las personas en “baja,” “intermedia,” y “alta” según sus años de educación. En este caso, hay un orden entre los grupos basado en el nivel de logro educativo. Como veremos, este orden puede o no proporcionar información sobre la variable dependiente. Factor es otro término utilizado para una variable explicativa categórica no ordenada.

Para las variables categóricas ordenadas, los analistas suelen asignar una puntuación numérica a cada resultado y tratar la variable como si fuera continua. Por ejemplo, si tuviéramos tres niveles de educación, podríamos emplear rangos y usar:

\[ \small{ \text{EDUCATION} = \begin{cases} 1 & \text{para educación baja} \\ 2 & \text{para educación intermedia} \\ 3 & \text{para educación alta.} \end{cases} } \]

Una alternativa sería utilizar una puntuación numérica que se aproxime a un valor subyacente de la categoría. Por ejemplo, podríamos usar:

\[ \small{ \text{EDUCATION} = \begin{cases} 6 & \text{para educación baja} \\ 10 & \text{para educación intermedia} \\ 14 & \text{para educación alta.} \end{cases} } \]

Esto da el número aproximado de años de escolaridad que completaron las personas en cada categoría.

La asignación de puntuaciones numéricas y el tratamiento de la variable como continua tiene implicaciones importantes para la interpretación en la modelización de regresión. Recordemos que el coeficiente de regresión es el cambio marginal en la respuesta esperada; en este caso, el \(\beta\) para EDUCATION evalúa el incremento en \(\mathrm{E }~y\) por unidad de cambio en EDUCATION. Si registramos EDUCATION como un rango en un modelo de regresión, entonces el \(\beta\) para EDUCATION corresponde al incremento en \(\mathrm{E }~y\) al pasar de EDUCATION=1 a EDUCATION=2 (de baja a intermedia); este incremento es el mismo que al pasar de EDUCATION=2 a EDUCATION=3 (de intermedia a alta). ¿Queremos modelar este incremento como igual? Esta es una suposición que el analista hace con esta codificación de EDUCATION; puede ser o no válida, pero ciertamente necesita ser reconocida.

Debido a esta interpretación de los coeficientes, los analistas rara vez usan rangos u otras puntuaciones numéricas para resumir variables categóricas no ordenadas. La forma más directa de manejar factores en la regresión es mediante el uso de variables binarias. Una variable categórica con \(c\) niveles puede representarse utilizando \(c\) variables binarias, una para cada categoría. Por ejemplo, supongamos que no estábamos seguros de la dirección del efecto de la educación y decidimos tratarla como un factor. Entonces, podríamos codificar \(c=3\) variables binarias: (1) una variable para indicar educación baja, (2) una para indicar educación intermedia, y (3) una para indicar educación alta. Estas variables binarias son a menudo conocidas como variables ficticias. En el análisis de regresión con un término de intercepción, utilizamos solo \(c-1\) de estas variables binarias; la variable restante entra implícitamente a través del término de intercepción. Al identificar una variable como un factor, la mayoría de los paquetes de software estadístico crearán automáticamente variables binarias para usted.

A través del uso de variables binarias, no utilizamos el orden de las categorías dentro de un factor. Debido a que no se hace ninguna suposición sobre el orden de las categorías, para el ajuste del modelo no importa qué variable se omita con respecto al ajuste del modelo. Sin embargo, sí importa para la interpretación de los coeficientes de regresión. Consideremos el siguiente ejemplo.

---

Ejemplo: Seguro de Vida Temporal - Continuado. Ahora volvemos al estado civil de los encuestados de la Encuesta de Finanzas del Consumidor (SCF). Recordemos que el estado civil no se mide de manera continua, sino que toma valores que caen en grupos distintos que tratamos como no ordenados. En el Capítulo 3, agrupamos a los encuestados según si eran o no “solteros”, donde ser soltero incluye nunca haberse casado, estar separado, divorciado, viudo, y no casado pero viviendo con una pareja. Ahora complementamos esto al considerar la variable categórica, MARSTAT, que representa el estado civil del encuestado. Esto puede ser:

• 1, para casado
• 2, para viviendo con una pareja
• 0, para otro (SCF desglosa aún más esta categoría en separado, divorciado, viudo, nunca casado, inaplicable, personas de 17 años o menos, y sin más personas).

Como antes, la variable dependiente es \(y =\) LNFACE, la cantidad que la compañía pagará en caso de fallecimiento del asegurado nombrado (en dólares logarítmicos). La Tabla 4.1 resume la variable dependiente según el nivel de la variable categórica. Esta tabla muestra que el estado civil “casado” es el más prevalente en la muestra y que los casados eligen tener la mayor cobertura de seguro de vida. La Figura 4.1 da una visión más completa de la distribución de LNFACE para cada uno de los tres tipos de estado civil. La tabla y la figura también sugieren que aquellos que viven juntos tienen menos cobertura de seguro de vida que las otras dos categorías.

Tabla 4.1: Estadísticas Resumidas de Logaritmo del Monto de Cobertura por Estado Civil

	MARSTAT	Número	Media	Desviación Estándar
Otro	0	57	10.958	1.566
Casado	1	208	12.329	1.822
Viviendo juntos	2	10	10.825	2.001
Total		275	11.990	1.871

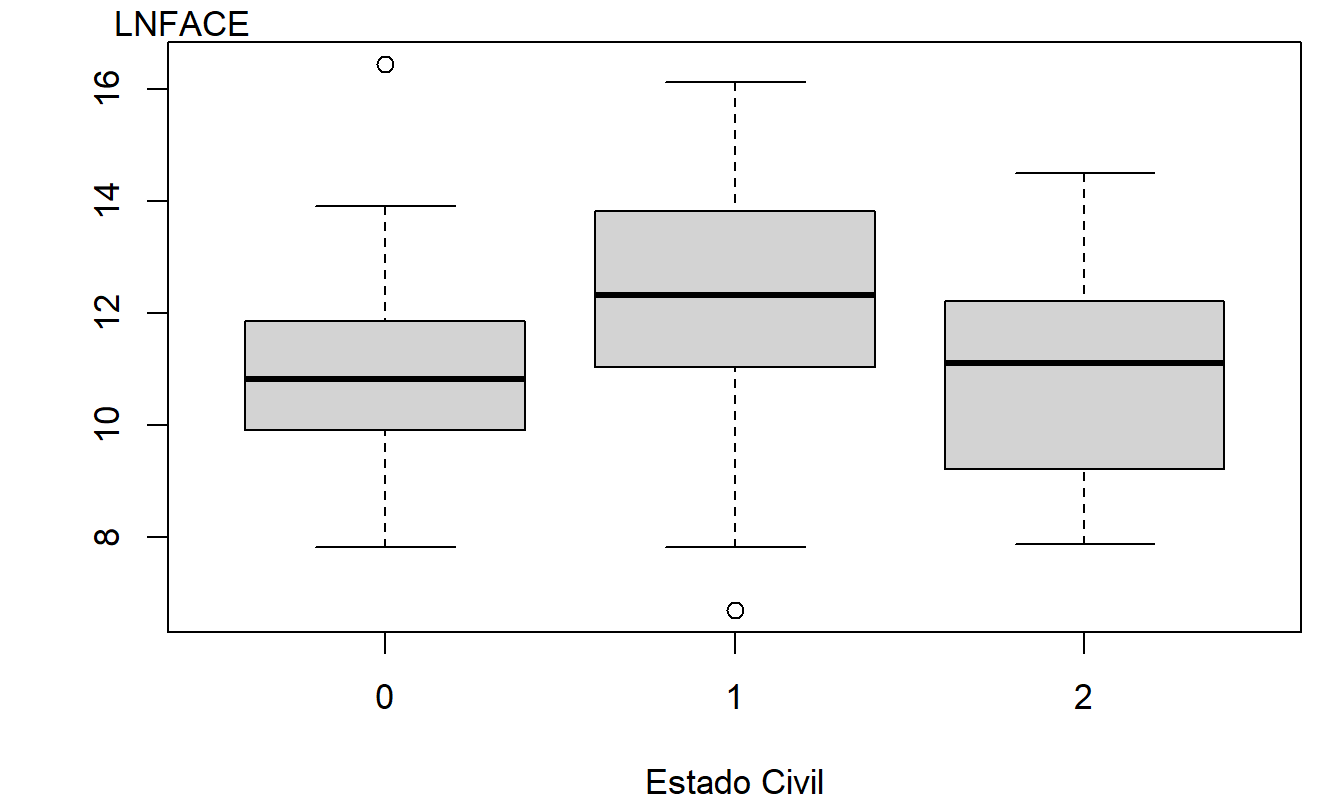
Figura 4.1: Diagramas de Caja del Logaritmo del Monto de Cobertura, por Nivel de Estado Civil

Código R para Producir la Tabla 4.1 y la Figura 4.1

tableout <- 
  data.frame(
    MARSTAT <- c(0,1,2,""),
    Número <- c(57, 208, 10, 275),
    Media <- c(10.958, 12.329, 10.825, 11.990),
    Desviación_Estándar <- c(1.566, 1.822, 2.001, 1.871)
    )

colnames(tableout) <- c("MARSTAT", "Número", "Media", "Desviación Estándar")
rownames(tableout) <- c("Otro", "Casado", "Viviendo juntos", "Total")

TableGen1(TableData=tableout , 
         TextTitle='Estadísticas Resumidas de Logaritmo del Monto de Cobertura por Estado Civil', 
         Align='crrr', Digits=3, ColumnSpec=1:3,
         ColWidth = ColWidth4) %>%
         kableExtra::column_spec(1, width =  "4cm") 

library(HH)
Term   <- read.csv("CSVData/TermLife.csv", header=TRUE)
Term2  <- subset(Term, FACE > 0)
LNFACE <- log(Term2$FACE)
LNINCOME <- log(Term2$INCOME)
MAR0   <- 1*(Term2$MARSTAT == 0)

#  FIGURA 4.1
par(mar=c(4.1,4,1,1), cex=1.1)
boxplot(LNFACE ~ MARSTAT, data=Term2, ylab="",
   xlab="Estado Civil")
mtext("LNFACE", side=2, at=17.2, las=1, cex=1.1, adj=.4)

¿Son las variables continuas y categóricas determinantes importantes de la respuesta? Para responder a esto, se realizó una regresión usando LNFACE como respuesta y cinco variables explicativas: tres continuas y dos binarias (para el estado civil). Recordemos que nuestras tres variables explicativas continuas son: LNINCOME (ingreso anual logarítmico), el número de años de EDUCATION del encuestado, y el número de miembros del hogar, NUMHH.

Para las variables binarias, primero definimos MAR0 como la variable binaria que toma el valor de uno si MARSTAT=0 y cero en caso contrario. De manera similar, definimos MAR1 y MAR2 como variables binarias que indican si MARSTAT=1 y MARSTAT=2, respectivamente. Existe una dependencia lineal perfecta entre estas tres variables binarias, ya que MAR0 + MAR1 + MAR2 = 1 para cualquier encuestado. Por lo tanto, solo necesitamos dos de las tres. Sin embargo, no hay una dependencia perfecta entre cualquiera de dos de las tres. Resulta que cor(MAR0, MAR1) = -0.90, cor(MAR0, MAR2) = -0.10, y cor(MAR1, MAR2) = -0.34.

Se realizó un modelo de regresión utilizando LNINCOME, EDUCATION, NUMHH, MAR0, y MAR2 como variables explicativas. La ecuación de regresión ajustada resulta ser:

\[ \small{ \widehat{y} = 3.395 + 0.452 \text{ LNINCOME} + 0.205 \text{ EDUCATION} + 0.248 \text{ NUMHH} - 0.557 \text{ MAR0} - 0.789 \text{ MAR2}. } \]

Para interpretar los coeficientes de regresión asociados con el estado civil, consideremos un encuestado que está casado. En este caso, MAR0=0, MAR1=1, y MAR2=0, de manera que:

\[ \small{ \widehat{y}_m = 3.395 + 0.452 \text{ LNINCOME} + 0.205 \text{ EDUCATION} + 0.248 \text{ NUMHH}. } \]

De manera similar, si el encuestado es codificado como viviendo juntos, entonces MAR0=0, MAR1=0, y MAR2=1, y:

\[ \small{ \widehat{y}_{lt} = 3.395 + 0.452 \text{ LNINCOME} + 0.205 \text{ EDUCATION} + 0.248 \text{ NUMHH} - 0.789. } \]

La diferencia entre \(\widehat{y}_m\) y \(\widehat{y}_{lt}\) es \(0.789.\) Así, podemos interpretar el coeficiente de regresión asociado con MAR2, \(-0.789\), como la diferencia en los valores ajustados para alguien que vive juntos en comparación con una persona similar que está casada (la categoría omitida).

De manera similar, podemos interpretar \(-0.557\) como la diferencia entre la categoría “otro” y la categoría de casados, manteniendo fijas las otras variables explicativas. Para la diferencia en los valores ajustados entre las categorías “otro” y “viviendo juntos”, podemos usar \(-0.557 - (-0.789) = 0.232.\)

Aunque la regresión se realizó utilizando MAR0 y MAR2, cualquier dos de las tres producirían la misma Tabla ANOVA (Tabla 4.2). Sin embargo, la elección de las variables binarias sí afecta los coeficientes de regresión. La Tabla 4.3 muestra tres modelos, omitiendo MAR1, MAR2, y MAR0, respectivamente. Para cada ajuste, los coeficientes asociados con las variables continuas permanecen iguales. Como hemos visto, las interpretaciones de las variables binarias son con respecto a la categoría omitida, conocida como el nivel de referencia. Aunque cambian de un modelo a otro, su interpretación general sigue siendo la misma. Es decir, si queremos estimar la diferencia en la cobertura entre la categoría “otro” y la categoría “viviendo juntos”, la estimación sería \(0.232\), sin importar el modelo.

Tabla 4.2: Seguro de Vida Temporal con Estado Civil - Tabla ANOVA

Fuente	Suma de Cuadrados	\(df\)	Cuadrado Medio
Regresión	343.28	5	68.66
Error	615.62	269	2.29
Total	948.90	274

Aunque los tres modelos en la Tabla 4.3 son iguales excepto por diferentes elecciones de parámetros, parecen diferentes. En particular, los \(t\)-ratios difieren y muestran diferentes apariencias de significancia estadística. Por ejemplo, ambos \(t\)-ratios asociados con el estado civil en el Modelo 2 son menores que 2 en valor absoluto, lo que sugiere que el estado civil es poco importante. En contraste, tanto el Modelo 1 como el Modelo 3 tienen al menos una variable binaria de estado civil que supera 2 en valor absoluto, lo que sugiere significancia estadística. Por lo tanto, se puede influir en la apariencia de significancia estadística al alterar la elección del nivel de referencia. Para evaluar la importancia general del estado civil (no solo cada variable binaria), la Sección 4.2 introducirá pruebas de conjuntos de coeficientes de regresión.

Tabla 4.3: Coeficientes de Regresión del Seguro de Vida Temporal con Estado Civil

	Coeficiente Modelo 1	Modelo 1 \(t\)-Ratio	Coeficiente Modelo 2	Modelo 2 \(t\)-Ratio	Coeficiente Modelo 3	Modelo 3 \(t\)-Ratio
LNINCOME	0.452	5.74	0.452	5.74	0.452	5.74
EDUCATION	0.205	5.3	0.205	5.3	0.205	5.3
NUMHH	0.248	3.57	0.248	3.57	0.248	3.57
Intercepto	3.395	3.77	3.395	2.74	2.838	3.34
MAR0	-0.557	-2.15	0.232	0.44
MAR1			0.789	1.59	0.557	2.15
MAR2	-0.789	-1.59			-0.232	-0.44

---

Ejemplo: ¿Cómo afecta el Compartir Costos en Planes de Seguro Médico a los Gastos en Salud? En uno de los muchos estudios que resultaron del Experimento de Seguro de Salud de Rand (HIE) introducido en la Sección 1.5, Keeler y Rolph (1988) investigaron los efectos del compartir costos en los planes de seguro médico. Para este estudio, 14 planes de seguro médico fueron agrupados por la tasa de coaseguro (el porcentaje pagado como gastos de bolsillo que variaba en 0, 25, 50 y 95%). Uno de los planes con 95% limitaba los gastos anuales de bolsillo en atención ambulatoria a 150 por persona (450 por familia), proporcionando en efecto un deducible ambulatorio individual. Este plan se analizó como un grupo separado, de manera que había \(c=5\) categorías de planes de seguro.

En la mayoría de los estudios de seguros, los individuos eligen planes de seguro, lo que hace difícil evaluar los efectos del compartir costos debido a la selección adversa. La selección adversa puede surgir porque los individuos con mala salud crónica son más propensos a elegir planes con menos compartir costos, lo que da la apariencia de que menos cobertura conduce a mayores gastos. En el HIE de Rand, los individuos fueron asignados aleatoriamente a los planes, eliminando así esta fuente potencial de sesgo.

Keeler y Rolph (1988) organizaron los gastos de un individuo en episodios de tratamiento; cada episodio contiene gastos asociados con un determinado ataque de enfermedad, condición crónica o procedimiento. Los episodios se clasificaron como hospitalarios, dentales o ambulatorios; esta clasificación se basó principalmente en diagnósticos, no en la ubicación de los servicios. Así, por ejemplo, los servicios ambulatorios que preceden o siguen a una hospitalización, así como los medicamentos y pruebas relacionados, se incluyeron como parte de un episodio hospitalario.

Para simplificar, aquí solo informamos resultados para episodios hospitalarios. Aunque las familias fueron asignadas aleatoriamente a los planes, Keeler y Rolph (1988) utilizaron métodos de regresión para controlar los atributos de los participantes y aislar los efectos del compartir costos en los planes. La Tabla 4.4 resume los coeficientes de regresión, basados en una muestra de \(n=1,967\) gastos por episodio. En esta regresión, el gasto logarítmico fue la variable dependiente.

La variable categórica de compartir costos se descompuso en cinco variables binarias para que no se impusiera ninguna forma funcional en la respuesta al seguro. Estas variables son “Co-ins25,” “Co-ins50,” y “Co-ins95,” para tasas de coaseguro del 25, 50 y 95%, respectivamente, y “Deducible Indiv” para el plan con deducibles individuales. La variable omitida es el plan de seguro gratuito con 0% de coaseguro. El HIE se llevó a cabo en seis ciudades; una variable categórica para controlar la ubicación se representó con cinco variables binarias, Dayton, Fitchburg, Franklin, Charleston y Georgetown, siendo Seattle la variable omitida. Se utilizó un factor categórico con \(c=6\) niveles para la edad y el sexo; las variables binarias en el modelo consistieron en “Edad 0-2,” “Edad 3-5,” “Edad 6-17,” “Mujer edad 18-65,” y “Hombre edad 46-65,” siendo la categoría omitida “Hombre edad 18-45.” Otras variables de control incluyeron una escala de estado de salud, el estado socioeconómico, el número de visitas médicas en el año anterior al experimento en una escala logarítmica y la raza.

La Tabla 4.4 resume los efectos de las variables. Como señalaron Keeler y Rolph, hubo grandes diferencias según la ubicación y la edad, aunque la regresión solo explicó \(R^2=11\%\) de la variabilidad. Para las variables de compartir costos, solo “Co-ins95” fue estadísticamente significativa, y esto solo al nivel del 5%, no al nivel del 1%.

El estudio de Keeler y Rolph (1988) examina otros tipos de gastos por episodio, así como la frecuencia de los gastos. Concluyeron que el compartir costos en los planes de seguro médico tiene poco efecto sobre la cantidad de gastos por episodio, aunque hay diferencias importantes en la frecuencia de episodios. Esto se debe a que un episodio de tratamiento está compuesto por dos decisiones. La cantidad de tratamiento es decidida conjuntamente entre el paciente y el médico y, en gran medida, no se ve afectada por el tipo de plan de seguro médico. La decisión de buscar tratamiento médico la toma el paciente; este proceso de toma de decisiones es más susceptible a los incentivos económicos en los aspectos de compartir costos de los planes de seguro médico.

Tabla 4.4: Coeficientes de Gastos por Episodio del Rand HIE

Variable	Coeficiente de Regresión	Variable	Coeficiente de Regresión
Intercepto	7.95
Dayton	0.13*	Co-ins25	0.07
Fitchburg	0.12	Co-ins50	0.02
Franklin	-0.01	Co-ins95	-0.13*
Charleston	0.20*	Deducible Indiv	-0.03
Georgetown	-0.18*
Escala de Salud	-0.02*	Edad 0-2	-0.63**
Estado Socioeconómico	0.03	Edad 3-5	-0.64**
Visitas Médicas	-0.03	Edad 6-17	-0.30**
Examen	-0.10*	Mujer edad 18-65	0.11
Negro	0.14*	Hombre edad 46-65	0.26

Nota: * significativo al 5%, ** significativo al 1%

Fuente: Keeler y Rolph (1988)

4.2 Inferencia Estadística para Varios Coeficientes

Puede ser útil examinar varios coeficientes de regresión al mismo tiempo. Por ejemplo, cuando se evalúa el efecto de una variable categórica con \(c\) niveles, necesitamos decir algo de manera conjunta sobre las \(c-1\) variables binarias que ingresan a la ecuación de regresión. Para hacer esto, la Sección 4.2.1 introduce un método para manejar combinaciones lineales de coeficientes de regresión. La Sección 4.2.2 muestra cómo probar varias combinaciones lineales, y la Sección 4.2.3 presenta otras aplicaciones de inferencia.

4.2.1 Conjuntos de Coeficientes de Regresión

Recordemos que nuestros coeficientes de regresión se especifican como \(\boldsymbol{\beta} = \left( \beta_0, \beta_1, \ldots, \beta_k \right)^{\prime},\) un vector de tamaño \((k+1) \times 1\). Será conveniente expresar combinaciones lineales de los coeficientes de regresión utilizando la notación \(\mathbf{C} \boldsymbol{\beta},\) donde \(\mathbf{C}\) es una matriz de tamaño \(p \times (k+1)\) que es especificada por el usuario y depende de la aplicación. Algunas aplicaciones involucran la estimación de \(\mathbf{C} \boldsymbol{\beta}\). Otras involucran probar si \(\mathbf{C} \boldsymbol{\beta}\) es igual a un valor específico conocido (denotado como \(\mathbf{d}\)). Llamamos a \(H_0:\mathbf{C \boldsymbol{\beta} = d}\) la hipótesis lineal general. Para demostrar la amplia variedad de aplicaciones en las que se pueden usar conjuntos de coeficientes de regresión, ahora presentamos una serie de casos especiales.

Caso Especial 1: Un Coeficiente de Regresión. En la Sección 3.4, investigamos la importancia de un solo coeficiente, digamos \(\beta_j\). Podemos expresar este coeficiente como \(\mathbf{C} \boldsymbol{\beta}\) eligiendo \(p=1\) y \(\mathbf{C}\) como un vector de \(1 \times (k+1)\) con un uno en la columna \((j+1)\) y ceros en las demás posiciones. Estas elecciones resultan en

\[ \mathbf{C \boldsymbol{\beta} =} \left( 0~\ldots~0~1~0~\ldots~0\right) \left( \begin{array}{c} \beta_0 \\ \vdots \\ \beta_k \end{array} \right) = \beta_j. \]

Caso Especial 2: Función de Regresión. Aquí, elegimos \(p=1\) y \(\mathbf{C}\) como un vector de \(1 \times (k+1)\) que representa la transpuesta de un conjunto de variables explicativas. Estas elecciones resultan en

\[ \mathbf{C \boldsymbol{\beta} =} \left( x_0, x_1, \ldots, x_k \right) \left( \begin{array}{c} \beta_0 \\ \vdots \\ \beta_k \end{array} \right) = \beta_0 x_0 + \beta_1 x_1 + \ldots + \beta_k x_k = \mathrm{E}~y, \] que es la función de regresión.

Caso Especial 3: Combinación Lineal de Coeficientes de Regresión. Cuando \(p=1\), usamos la convención de que las letras en minúscula en negrita son vectores y tomamos \(\mathbf{C = c^{\prime}} = \left( c_0, \ldots, c_k \right)^{\prime}\). En este caso, \(\mathbf{C} \boldsymbol{\beta}\) es una combinación lineal genérica de los coeficientes de regresión

\[ \mathbf{C} \boldsymbol{\beta} = \mathbf{c}^{\prime} {\boldsymbol \beta} = c_0 \beta_0 + \ldots + c_k \beta_k . \]

Caso Especial 4: Prueba de Igualdad de Coeficientes de Regresión. Supongamos que el interés radica en probar \(H_0: \beta_1 = \beta_2\). Para este propósito, tomamos \(p=1\), \(\mathbf{c}^{\prime} = \left( 0, 1, -1, 0, \ldots, 0\right)\), y \(\mathbf{d} = 0\). Con estas elecciones, tenemos

\[ \mathbf{C \boldsymbol{\beta} = c^{\prime} \boldsymbol{\beta} =} \left( 0, 1, -1, 0, \ldots, 0\right) \left( \begin{array}{c} \beta_0 \\ \vdots \\ \beta_k \end{array} \right) = \beta_1 - \beta_2 = 0, \]

de modo que la hipótesis lineal general se reduce a \(H_0: \beta_1 = \beta_2\).

Caso Especial 5: Adecuación del Modelo. Es costumbre en el análisis de regresión presentar una prueba de si alguna de las variables explicativas es útil para explicar la respuesta. Formalmente, esto es una prueba de la hipótesis nula \(H_0:\beta_1=\beta_2=\ldots=\beta_k=0\). Es importante notar que, como convención, no se prueba si el intercepto es cero. Para probar esto usando la hipótesis lineal general, elegimos \(p=k\), \(\mathbf{d}=\left( 0~\ldots~0\right)^{\prime}\) como un vector de tamaño \(k \times 1\) lleno de ceros y \(\mathbf{C}\) como una matriz de tamaño \(k \times (k+1)\) tal que

\[ \small{ \mathbf{C \boldsymbol{\beta} =}\left( \begin{array}{ccccc} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end{array} \right) \left( \begin{array}{c} \beta_0 \\ \vdots \\ \beta_k \end{array} \right) =\left( \begin{array}{c} \beta_1 \\ \vdots \\ \beta_k \end{array} \right) =\left( \begin{array}{c} 0 \\ \vdots \\ 0 \end{array} \right) =\mathbf{d}. } \]

Caso Especial 6: Prueba de Partes del Modelo. Supongamos que estamos interesados en comparar una función de regresión completa

\[ \mathrm{E~}y = \beta_0 + \beta_1 x_1 +\ldots + \beta_k x_k + \beta_{k+1} x_{k+1} + \ldots + \beta_{k+p} x_{k+p} \] con una función de regresión reducida,

\[ \mathrm{E~}y = \beta_0 + \beta_1 x_1 + \ldots + \beta_k x_k. \] Comenzando con la regresión completa, vemos que si se cumple la hipótesis nula \(H_0:\beta_{k+1} = \ldots = \beta_{k+p} = 0\), entonces llegamos a la regresión reducida. Para ilustrar, las variables \(x_{k+1}, \ldots, x_{k+p}\) pueden referirse a varias variables binarias que representan una variable categórica y nuestro interés radica en si la variable categórica es importante. Para probar la importancia de la variable categórica, queremos ver si las variables binarias \(x_{k+1}, \ldots, x_{k+p}\) afectan conjuntamente a las variables dependientes.

Para probar esto utilizando la hipótesis lineal general, elegimos \(\mathbf{d}\) y \(\mathbf{C}\) tal que

\[ \small{ \mathbf{C \boldsymbol{\beta} =}\left( \begin{array}{ccccccc} 0 & \cdots & 0 & 1 & 0 & \cdots & 0 \\ 0 & \cdots & 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & 0 & 0 & \cdots & 1 \end{array} \right) \left( \begin{array}{c} \beta_0 \\ \vdots \\ \beta_k \\ \beta_{k+1} \\ \vdots \\ \beta_{k+p} \end{array} \right) =\left( \begin{array}{c} \beta_{k+1} \\ \vdots \\ \beta_{k+p} \end{array} \right) =\left( \begin{array}{c} 0 \\ \vdots \\ 0 \end{array} \right) =\mathbf{d}. } \]

De una lista de \(k+p\) variables \(x_1, \ldots, x_{k+p}\), puedes eliminar cualquier \(p\) que consideres apropiado. Las variables adicionales no necesitan ser las últimas \(p\) en la especificación de la regresión. Eliminar \(x_{k+1}, \ldots, x_{k+p}\) es solo por conveniencia notacional.

4.2.2 La Hipótesis Lineal General

Para resumir, la hipótesis lineal general se puede expresar como \(H_0:\mathbf{C \boldsymbol{\beta} = d}\). Aquí, \(\mathbf{C}\) es una matriz de \(p \times (k+1)\), \(\mathbf{d}\) es un vector de \(p \times 1\), y tanto \(\mathbf{C}\) como \(\mathbf{d}\) son especificados por el usuario y dependen de la aplicación en cuestión. Aunque \(k+1\) es el número de coeficientes de regresión, \(p\) es el número de restricciones bajo \(H_0\) sobre estos coeficientes. (Para aquellos lectores con conocimiento de álgebra matricial avanzada, \(p\) es el rango de \(\mathbf{C}\)). Esta hipótesis nula se prueba contra la alternativa \(H_a:\mathbf{C \boldsymbol{\beta} \neq d}\). Esto puede ser obvio, pero requerimos que \(p \leq k+1\) porque no podemos probar más restricciones que los parámetros libres.

Para entender la base del procedimiento de prueba, primero recordemos algunas de las propiedades básicas de los estimadores de los coeficientes de regresión descritos en la Sección 3.3. Sin embargo, nuestro objetivo ahora es entender las propiedades de las combinaciones lineales de los coeficientes de regresión especificadas por \(\mathbf{C \boldsymbol{\beta}}\). Un estimador natural de esta cantidad es \(\mathbf{Cb}\). Es fácil ver que \(\mathbf{Cb}\) es un estimador insesgado de \(\mathbf{C \boldsymbol{\beta}}\), porque \(\mathrm{E~}\mathbf{Cb = C}\mathrm{E~}\mathbf{b = C \boldsymbol{\beta}}\). Además, la varianza es \(\mathrm{Var}\left( \mathbf{Cb}\right) \mathbf{= C}\mathrm{Var}\left( \mathbf{b}\right) \mathbf{C}^{\prime}\) \(=\sigma^2 \mathbf{C}\left( \mathbf{X^{\prime}X}\right)^{-1} \mathbf{C}^{\prime}\). Para evaluar la diferencia entre \(\mathbf{d}\), el valor hipotetizado de \(\mathbf{C \boldsymbol{\beta}}\), y su valor estimado, \(\mathbf{Cb}\), utilizamos la siguiente estadística:

\[ F-\text{ratio}=\frac{(\mathbf{Cb-d)}^{\prime}\left( \mathbf{C}\left( \mathbf{X^{\prime}X} \right)^{-1} \mathbf{C}^{\prime}\right)^{-1}(\mathbf{Cb-d)}}{ps_{full}^2}. \tag{4.1} \]

Aquí, \(s_{full}^2\) es el error cuadrático medio del modelo de regresión completo. Usando la teoría de modelos lineales, se puede comprobar que la estadística \(F\)-ratio sigue una distribución \(F\) con grados de libertad del numerador \(df_1=p\) y grados de libertad del denominador \(df_2=n-(k+1)\). Tanto la estadística como la distribución teórica llevan el nombre de R. A. Fisher, un científico y estadístico renombrado que hizo mucho para avanzar la estadística como ciencia en la primera mitad del siglo XX.

Al igual que la distribución normal y la distribución \(t\), la distribución \(F\) es una distribución continua. La distribución \(F\) es la distribución muestral para el \(F\)-ratio y es proporcional a la razón de dos sumas de cuadrados, cada una de las cuales es positiva o cero. Así, a diferencia de la distribución normal y la distribución \(t\), la distribución \(F\) solo toma valores no negativos. Recordemos que la distribución \(t\) está indexada por un único parámetro de grados de libertad. La distribución \(F\) está indexada por dos parámetros de grados de libertad: uno para el numerador, \(df_1\), y uno para el denominador, \(df_2\). El Apéndice A3.4 proporciona detalles adicionales.

La estadística de prueba en la ecuación (4.1) es compleja en su forma. Afortunadamente, existe una alternativa que es más sencilla de implementar e interpretar; esta alternativa se basa en el principio de la suma de cuadrados adicional.

Procedimiento para Probar la Hipótesis Lineal General

1. Ejecuta la regresión completa y obtén la suma de cuadrados del error y el error cuadrático medio, los cuales etiquetamos como \((Error~SS)_{full}\) y \(s_{full}^2\), respectivamente.
2. Considera el modelo asumiendo que la hipótesis nula es verdadera. Ejecuta una regresión con este modelo y obtén la suma de cuadrados del error, la cual etiquetamos como \((Error~SS)_{reduced}\).
3. Calcula \[ F-\text{ratio}=\frac{(Error~SS)_{reduced}-(Error~SS)_{full}}{ps_{full}^2}. \tag{4.2} \]
4. Rechaza la hipótesis nula en favor de la alternativa si el \(F\)-ratio excede un valor \(F\). El valor \(F\) es un percentil de la distribución \(F\) con \(df_1=p\) y \(df_2=n-(k+1)\) grados de libertad. El percentil es uno menos el nivel de significancia de la prueba. Siguiendo nuestra notación con la distribución \(t\), denotamos este percentil como \(F_{p,n-(k+1),1-\alpha}\), donde \(\alpha\) es el nivel de significancia.

Este procedimiento es comúnmente conocido como una prueba \(F\).

La Sección 4.7.2 proporciona las bases matemáticas. Para entender el principio de la suma de cuadrados adicional, recordemos que la suma de cuadrados del error para el modelo completo se determina como el valor mínimo de

\[ SS(b_0^{\ast}, \ldots, b_k^{\ast}) = \sum_{i=1}^{n} \left( y_i - \left( b_0^{\ast} + \ldots + b_k^{\ast} x_{i,k} \right) \right)^2. \]

Aquí, \(SS(b_0^{\ast}, \ldots, b_k^{\ast})\) es una función de \(b_0^{\ast}, \ldots, b_k^{\ast}\) y \((Error~SS)_{full}\) es el mínimo sobre todos los valores posibles de \(b_0^{\ast}, \ldots, b_k^{\ast}\). De manera similar, \((Error~SS)_{reduced}\) es la mínima suma de cuadrados del error bajo las restricciones en la hipótesis nula. Debido a que hay menos posibilidades bajo la hipótesis nula, tenemos que

\[ (Error~SS)_{full} \leq (Error~SS)_{reduced}. \tag{4.3} \]

Para ilustrar, consideremos nuestro primer caso especial donde \(H_0 : \beta_j = 0\). En este caso, la diferencia entre los modelos completo y reducido equivale a eliminar una variable. Una consecuencia de la ecuación (4.3) es que, al agregar variables a un modelo de regresión, la suma de cuadrados del error nunca aumenta (y, de hecho, generalmente disminuye). Por lo tanto, agregar variables a un modelo de regresión aumenta \(R^2\), el coeficiente de determinación.

¿Cuán grande debe ser una disminución en la suma de cuadrados del error para que sea estadísticamente significativa? Intuitivamente, se puede ver el cociente \(F\) como la diferencia en la suma de cuadrados del error dividida por el número de restricciones, \(\frac{(Error~SS)_{reduced}-(Error~SS)_{full}}{p}\), y luego reescalada por la mejor estimación del término de varianza, el \(s^2\), del modelo completo. Bajo la hipótesis nula, esta estadística sigue una distribución \(F\) y podemos comparar la estadística de prueba con esta distribución para ver si es inusualmente grande.

Usando la relación \(Regression~SS = Total~SS - Error~SS\), podemos re-expresar la diferencia en la suma de cuadrados del error como

\[ (Error~SS)_{reduced} - (Error~SS)_{full} = (Regression~SS)_{full} - (Regression~SS)_{reduced}. \]

Esta diferencia se conoce como una Suma de Cuadrados Tipo III. Al probar la importancia de un conjunto de variables explicativas, \(x_{k+1}, \ldots, x_{k+p}\), en presencia de \(x_1, \ldots, x_k\), encontrarás que muchos paquetes estadísticos calculan esta cantidad directamente en una sola ejecución de regresión. La ventaja de esto es que permite al analista realizar una prueba \(F\) usando una sola ejecución de regresión, en lugar de dos ejecuciones de regresión como en nuestro procedimiento de cuatro pasos descrito anteriormente.

---

Ejemplo: Seguro de Vida Temporal - Continuación. Antes de discutir la lógica y las implicaciones de la prueba \(F\), vamos a ilustrar su uso. En el ejemplo del Seguro de Vida Temporal, supongamos que deseamos entender el impacto del estado civil. La Tabla 4.3 presentó un mensaje mixto en términos de cocientes \(t\); a veces eran estadísticamente significativos y otras veces no. Sería útil tener una prueba formal para dar una respuesta definitiva, al menos en términos de significancia estadística. Específicamente, consideramos un modelo de regresión utilizando LNINCOME, EDUCATION, NUMHH, MAR0, y MAR2 como variables explicativas. La ecuación del modelo es

\[ \small{ \begin{array}{ll} y &= \beta_0 + \beta_1 \text{LNINCOME} + \beta_2 \text{EDUCATION} + \beta_3 \text{NUMHH} \\ & \ \ \ \ + \beta_4 \text{MAR0} + \beta_5 \text{MAR2}. \end{array} } \]

Nuestro objetivo es probar \(H_0: \beta_4 = \beta_5 = 0\).

1. Comenzamos ejecutando un modelo de regresión con todas las \(k+p=5\) variables. Los resultados se informaron en la Tabla 4.2, donde vimos que \((Error~SS)_{full} = 615.62\) y \(s_{full}^2 = (1.513)^2 = 2.289\).
2. El siguiente paso es ejecutar el modelo reducido sin MAR0 y MAR2. Esto se hizo en la Tabla 3.3 del Capítulo 3, donde vimos que \((Error~SS)_{reduced} = 630.43\).
3. Luego calculamos la estadística de prueba \[ \small{ F-\text{ratio} = \frac{(Error~SS)_{reduced} - (Error~SS)_{full}}{ps_{full}^2} = \frac{630.43 - 615.62}{2 \times 2.289} = 3.235. } \]
4. El cuarto paso compara la estadística de prueba con una distribución \(F\) con \(df_1=p=2\) y \(df_2 = n-(k+p+1) = 269\) grados de libertad. Usando un nivel de significancia del 5%, resulta que el percentil 95 es \(F-\text{ratio} \approx 3.029\). El valor \(p\) correspondiente es \(\Pr(F > 3.235) = 0.0409\). Al nivel de significancia del 5%, rechazamos la hipótesis nula \(H_0: \beta_4 = \beta_5 = 0\). Esto sugiere que es importante utilizar el estado civil para entender la cobertura de seguro de vida temporal, incluso en presencia de ingresos, educación y número de miembros del hogar.

---

Algunos Casos Especiales

La prueba de hipótesis lineales general está disponible cuando puedes expresar un modelo como un subconjunto de otro. Por esta razón, es útil pensar en ella como una herramienta para comparar modelos “más pequeños” con modelos “más grandes”. Sin embargo, el modelo más pequeño debe ser un subconjunto del modelo más grande. Por ejemplo, la prueba de hipótesis lineales general no se puede usar para comparar las funciones de regresión \(\mathrm{E~}y = \beta_0 + \beta_7 x_7\) frente a \(\mathrm{E~}y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + \beta_4 x_4\). Esto se debe a que la primera, función más pequeña, no es un subconjunto de la segunda, función más grande.

La prueba de hipótesis lineales general se puede usar en muchas ocasiones, aunque no siempre es necesaria. Por ejemplo, supongamos que deseamos probar \(H_0:\beta_k=0\). Ya hemos visto que esta hipótesis nula se puede examinar usando la prueba del cociente \(t\). En este caso especial, resulta que \((t-\textrm{ratio})^2=F-\textrm{ratio}\). Así, estas pruebas son equivalentes para probar \(H_0:\beta_k=0\) frente a \(H_a:\beta_k \neq 0\). La prueba \(F\) tiene la ventaja de que funciona para más de un predictor, mientras que la prueba \(t\) tiene la ventaja de que se pueden considerar alternativas unilaterales. Por lo tanto, ambas pruebas son consideradas útiles.

Dividiendo el numerador y el denominador de la ecuación (4.2) por \(Total~SS\), la estadística de prueba también se puede escribir como:

\[ F-\textrm{ratio}=\frac{\left( R_{full}^2-R_{reduced}^2\right) /p}{\left( 1-R_{full}^2\right) / (n-(k+1))}. \tag{4.4} \]

La interpretación de esta expresión es que el cociente \(F\) mide la disminución en el coeficiente de determinación, \(R^2\).

La expresión en la ecuación (4.4) es particularmente útil para probar la adecuación del modelo, nuestro Caso Especial 5. En este caso, \(p=k\), y la suma de cuadrados de regresión bajo el modelo reducido es cero. Así, tenemos

\[ \small{ F-\textrm{ratio}=\frac{\left( (Regression~SS)_{full}\right) /k}{s_{full}^2} =\frac{(Regression~MS)_{full}}{(Error~SS)_{full}}. } \]

Esta estadística de prueba es una característica regular de la tabla ANOVA para muchos paquetes estadísticos.

Por ejemplo, en nuestro ejemplo de Seguro de Vida Temporal, probar la adecuación del modelo significa evaluar \(H_0: \beta_1 = \beta_2 = \beta_3 = \beta_4 = \beta_5 = 0\). En la Tabla 4.2, el cociente \(F\) es 68.66 / 2.29 = 29.98. Con \(df_1=5\) y \(df_2 = 269\), el valor \(F\) es aproximadamente 2.248 y el valor \(p\) correspondiente es \(\Pr(F > 29.98) \approx 0\). Esto nos lleva a rechazar firmemente la idea de que las variables explicativas no son útiles para entender la cobertura del seguro de vida temporal, reafirmando lo que aprendimos en el análisis gráfico y de correlación. Cualquier otro resultado sería sorprendente.

Para otra expresión, dividiendo por \(Total~SS\), podemos escribir

\[ F-\textrm{ratio}=\frac{R^2}{1-R^2}\frac{n-(k+1)}{k}. \]

Dado que tanto el cociente \(F\) como \(R^2\) son medidas del ajuste del modelo, parece intuitivamente plausible que estén relacionados de alguna manera. Una consecuencia de esta relación es que, a medida que \(R^2\) aumenta, también lo hace el cociente \(F\) y viceversa. El cociente \(F\) se usa porque su distribución muestral es conocida bajo una hipótesis nula, por lo que podemos hacer afirmaciones sobre significancia estadística. La medida \(R^2\) se usa debido a las interpretaciones fáciles asociadas con ella.

4.2.3 Estimando y Prediciendo Varios Coeficientes

Estimación de Combinaciones Lineales de Coeficientes de Regresión

En algunas aplicaciones, el principal interés es estimar una combinación lineal de los coeficientes de regresión. Para ilustrar, recordemos que en la Sección 3.5 desarrollamos una función de regresión para las contribuciones caritativas de un individuo (\(y\)) en términos de sus salarios (\(x\)). En esta función, hubo un cambio abrupto en la función en \(x=97,500\). Para modelarlo, definimos la variable binaria \(z\) para que sea cero si \(x<97,500\) y uno si \(x \geq 97,500\), y la función de regresión \(\mathrm{E~}y = \beta_0 + \beta_1 x + \beta_2 z(x - 97,500)\). Así, el cambio marginal esperado en las contribuciones por cambio en el salario para salarios superiores a \(97,500\) es \(\frac{\partial \left( \mathrm{E~}y\right)}{\partial x} = \beta_1 + \beta_2\).

Para estimar \(\beta_1 + \beta_2\), un estimador razonable es \(b_1 + b_2\), el cual está disponible en el software estándar de regresión. Además, también nos gustaría calcular errores estándar para \(b_1 + b_2\) que se pueden utilizar, por ejemplo, para determinar un intervalo de confianza para \(\beta_1 + \beta_2\). Sin embargo, \(b_1\) y \(b_2\) suelen estar correlacionados, por lo que el cálculo del error estándar de \(b_1 + b_2\) requiere la estimación de la covarianza entre \(b_1\) y \(b_2\).

La estimación de \(\beta_1 + \beta_2\) es un ejemplo de nuestro Caso Especial 3, que considera combinaciones lineales de coeficientes de regresión de la forma \(\mathbf{c}^{\prime} \boldsymbol \beta = c_0 \beta_0 + c_1 \beta_1 + \ldots + c_k \beta_k\). Para nuestro ejemplo de contribuciones caritativas, elegiríamos \(c_1 = c_2 = 1\) y los demás \(c\)’s igual a cero.

Para estimar \(\mathbf{c}^{\prime} \boldsymbol \beta\), reemplazamos el vector de parámetros por el vector de estimadores y usamos \(\mathbf{c}^{\prime} \mathbf{b}\). Para evaluar la fiabilidad de este estimador, como en la Sección 4.2.2, tenemos que \(\mathrm{Var}\left( \mathbf{c}^{\prime} \mathbf{b}\right) = \sigma^2 \mathbf{c}^{\prime}(\mathbf{X^{\prime} X})^{-1} \mathbf{c}\). Así, podemos definir la desviación estándar estimada, o error estándar, de \(\mathbf{c}^{\prime} \mathbf{b}\) como

\[ se\left( \mathbf{c}^{\prime} \mathbf{b} \right) = s \sqrt{\mathbf{c}^{\prime} (\mathbf{X}^{\prime} \mathbf{X})^{-1} \mathbf{c}}. \]

Con esta cantidad, un intervalo de confianza del \(100(1 - \alpha) \%\) para \(\mathbf{c}^{\prime} \boldsymbol \beta\) es

\[ \mathbf{c}^{\prime} \mathbf{b} \pm t_{n - (k + 1), 1 - \alpha / 2} ~ se(\mathbf{c}^{\prime} \mathbf{b}). \tag{4.5} \]

El intervalo de confianza en la ecuación (4.5) es válido bajo las Suposiciones F1-F5. Si elegimos que \(\mathbf{c}\) tenga un “1” en la \((j + 1)^{\text{st}}\) fila y ceros en los demás, entonces \(\mathbf{c}^{\prime} \boldsymbol \beta = \beta_j\), \(\mathbf{c}^{\prime} \mathbf{b} = b_j\), y

\[ se(b_j) = s \sqrt{(j + 1)^{\text{st}}~ \textit{elemento diagonal de } (\mathbf{X}^{\prime} \mathbf{X})^{-1}}. \]

Por lo tanto, la ecuación (4.5) proporciona una base teórica para los intervalos de confianza de los coeficientes de regresión individuales introducidos en la ecuación (3.10) de la Sección 3.4 y lo generaliza a combinaciones lineales arbitrarias de los coeficientes de regresión.

Otra aplicación importante de la ecuación (4.5) es la elección de \(\mathbf{c}\) correspondiente a un conjunto de variables explicativas de interés, digamos, \(\mathbf{x}_{\ast} = \left( 1, x_{\ast 1}, x_{\ast 2}, \ldots, x_{\ast k} \right)^{\prime}\). Estas pueden corresponder a una observación dentro del conjunto de datos o a un punto fuera de los datos disponibles. El parámetro de interés, \(\mathbf{c}^{\prime} \boldsymbol \beta = \mathbf{x}_{\ast}^{\prime} \boldsymbol \beta\), es la respuesta esperada o la función de regresión en ese punto. Entonces, \(\mathbf{x}_{\ast}^{\prime} \mathbf{b}\) proporciona un estimador puntual y la ecuación (4.5) proporciona el intervalo de confianza correspondiente.

Intervalos de Predicción

La predicción es un objetivo inferencial que está estrechamente relacionado con la estimación de la función de regresión en un punto. Supongamos que, al considerar las contribuciones caritativas, conocemos los salarios de un individuo (y por lo tanto si los salarios superan los \(97,500\)) y deseamos predecir la cantidad de contribuciones caritativas. En general, asumimos que el conjunto de variables explicativas \(\mathbf{x}_{\ast}\) es conocido y deseamos predecir la respuesta correspondiente \(y_{\ast}\). Esta nueva respuesta sigue las suposiciones descritas en la Sección 3.2. Específicamente, la respuesta esperada es \(\mathrm{E~}y_{\ast} = \mathbf{x}_{\ast}^{\prime} \boldsymbol \beta\), \(\mathbf{x}_{\ast}\) es no estocástica, \(\mathrm{Var~}y_{\ast} = \sigma^2\), \(y_{\ast}\) es independiente de \(\{y_1, \ldots, y_{n}\}\) y está distribuida normalmente. Bajo estas suposiciones, un intervalo de predicción del \(100(1 - \alpha)\%\) para \(y_{\ast}\) es

\[ \mathbf{x}_{\ast}^{\prime} \mathbf{b} \pm t_{n - (k + 1), 1 - \alpha / 2} ~ s \sqrt{1 + \mathbf{x}_{\ast}^{\prime} (\mathbf{X}^{\prime} \mathbf{X})^{-1} \mathbf{x}_{\ast}}. \tag{4.6} \]

La ecuación (4.6) generaliza el intervalo de predicción introducido en la Sección 2.4.

4.3 Modelo ANOVA de Un Factor

La Sección 4.1 mostró cómo incorporar variables categóricas no ordenadas, o factores, en un modelo de regresión lineal mediante el uso de variables binarias. Los factores son importantes en la investigación en ciencias sociales; pueden usarse para clasificar a las personas por género, etnia, estado civil, etc., o clasificar empresas por región geográfica, estructura organizativa, y así sucesivamente. En los estudios de seguros, las aseguradoras usan factores para categorizar a los asegurados según un “sistema de clasificación de riesgos.” Aquí, la idea es crear grupos de asegurados con características de riesgo similares que tendrán experiencias de reclamaciones similares. Estos grupos forman la base del precio del seguro, de modo que a cada asegurado se le cobra un monto adecuado a su categoría de riesgo. Este proceso a veces se conoce como “segmentación.”

Aunque los factores pueden representarse como variables binarias en un modelo de regresión lineal, estudiamos los modelos de un factor como una unidad separada porque:

• El método de los mínimos cuadrados es mucho más simple, evitando la necesidad de invertir matrices de alta dimensión.
• Las interpretaciones resultantes de los coeficientes son más sencillas.

El modelo de un factor sigue siendo un caso especial del modelo de regresión lineal. Por lo tanto, no se necesita teoría estadística adicional para establecer sus capacidades de inferencia estadística.

Para establecer la notación para el modelo ANOVA de un factor, ahora consideramos el siguiente ejemplo.

---

Ejemplo: Reclamaciones de Seguros de Automóviles. Examinamos la experiencia de reclamaciones de un gran asegurador de propiedades y accidentes del medio oeste de los Estados Unidos para seguros de automóviles particulares. La variable dependiente es la cantidad pagada en una reclamación cerrada, en dólares (reclamaciones que no se cerraron al final del año se manejan por separado). Las aseguradoras categorizan a los asegurados según un sistema de clasificación de riesgos. El sistema de clasificación de riesgos de esta aseguradora se basa en:

• Características del operador del automóvil (edad, género, estado civil y si es el conductor principal u ocasional de un automóvil).
• Características del vehículo (uso en la ciudad o en el campo, si el vehículo se usa para ir a la escuela o al trabajo, para negocios o placer, y si se usa para ir al trabajo, la distancia aproximada del trayecto).

Estos factores se resumen en la variable categórica de clase de riesgo CLASS. La Tabla 4.5 muestra 18 clases de riesgo - no se proporciona información adicional de clasificación aquí para proteger los intereses propietarios de la aseguradora.

La Tabla 4.5 resume los resultados de \(n=6,773\) reclamaciones para conductores de 50 años o más. Podemos ver que la reclamación mediana varía desde un mínimo de 707.40 (CLASE F7) hasta un máximo de 1,231.25 (CLASE C72). La distribución de las reclamaciones resulta ser asimétrica, por lo que consideramos \(y\) = reclamaciones logarítmicas. La tabla presenta medias, medianas y desviaciones estándar. Dado que la distribución de las reclamaciones logarítmicas es menos asimétrica, las medias están cerca de las medianas. La Figura 4.2 muestra la distribución de las reclamaciones logarítmicas por clase de riesgo.

Tabla 4.5: Estadísticas Resumidas de Reclamaciones de Automóviles por Clase de Riesgo

	1	2	3	4	5	6
Clase	C1	C11	C1A	C1B	C1C	C2
Número	726	1151	77	424	38	61
Mediana (dólares)	948.86	1,013.81	925.48	1,026.73	1,001.73	851.20
Mediana (en dólares log)	6.855	6.921	6.830	6.934	6.909	6.747
Media (en dólares log)	6.941	6.952	6.866	6.998	6.786	6.801
Desv. estándar (en dólares log)	1.064	1.074	1.072	1.068	1.110	0.948
Clase	C6	C7	C71	C72	C7A	C7B
Número	911	913	1129	85	113	686
Mediana (dólares)	1,011.24	957.68	960.40	1,231.25	1,139.93	1,113.13
Mediana (en dólares log)	6.919	6.865	6.867	7.116	7.039	7.015
Media (en dólares log)	6.926	6.901	6.954	7.183	7.064	7.072
Desv. estándar (en dólares log)	1.115	1.058	1.038	0.988	1.021	1.103
Clase	C7C	F1	F11	F6	F7	F71
Número	81	29	40	157	59	93
Mediana (dólares)	1,200.00	1,078.04	774.79	1,105.04	707.40	1,118.73
Mediana (en dólares log)	7.090	6.983	6.652	7.008	6.562	7.020
Media (en dólares log)	7.244	7.004	6.804	6.910	6.577	6.935
Desv. estándar (en dólares log)	0.944	0.996	1.212	1.193	0.897	0.983

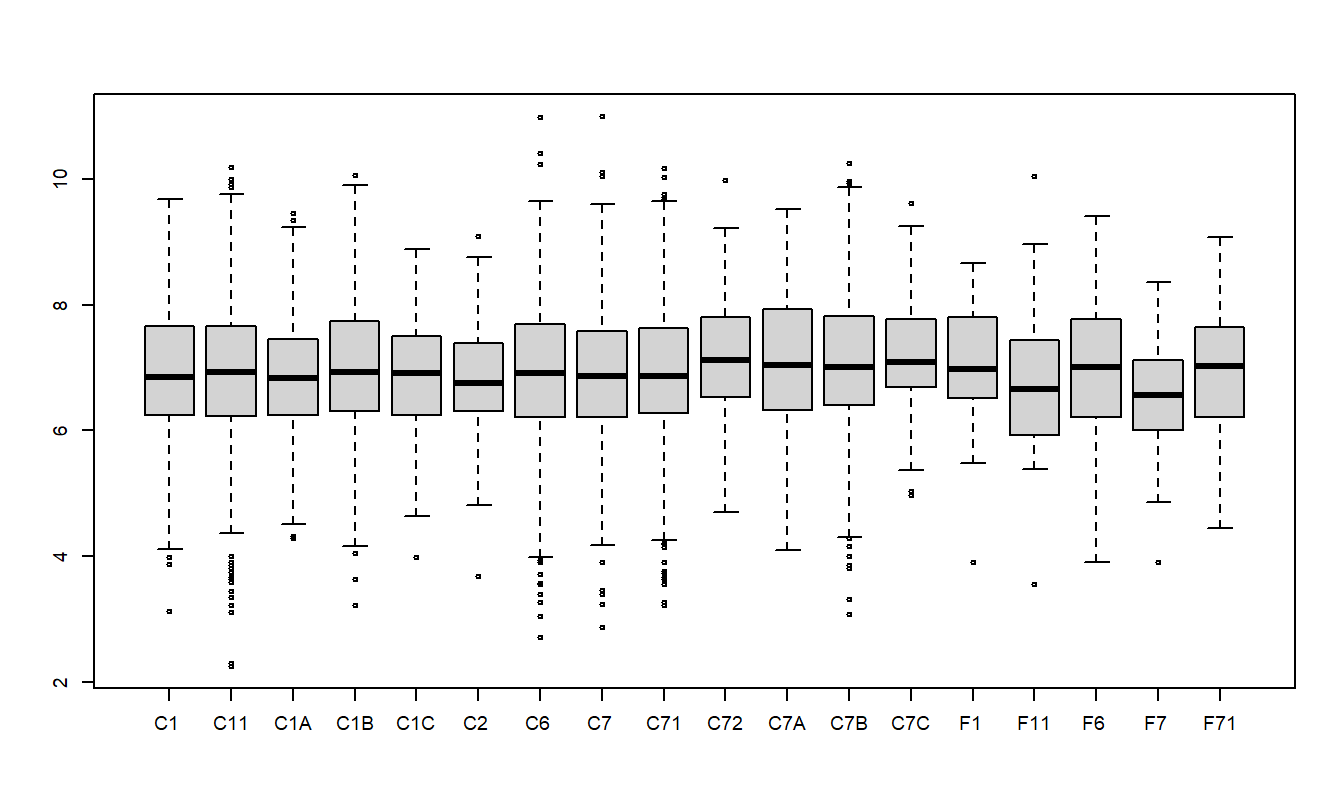
Figura 4.2: Diagramas de Caja de Reclamaciones Logarítmicas por Clase de Riesgo

Código R para Producir la Tabla 4.5 y la Figura 4.2

AutoC   <- read.csv("CSVData/AutoClaims.csv", header=TRUE)
#  CREAR UNA TABLA DE MEDIAS Y DESVIACIONES ESTÁNDAR
library(Hmisc)
t1 <- summarize(log(AutoC$PAID), AutoC$CLASS, length ) 
t2 <- summarize(AutoC$PAID, AutoC$CLASS, median) 
t3 <- summarize(log(AutoC$PAID), AutoC$CLASS, median) 
t4 <- summarize(log(AutoC$PAID), AutoC$CLASS, mean) 
t5 <- summarize(log(AutoC$PAID), AutoC$CLASS, sd) 
tablemat <- cbind(t1,
                  format(round(t2[2], digits = 2), big.mark = ','),
                  round(t3[2], digits = 3),
                  round(t4[2], digits = 3),
                  round(t5[2], digits = 3))
block1 <-  t(tablemat[1:6,])
block2 <- t(tablemat[7:12,])
block3 <- t(tablemat[13:18,])

bigblock <- rbind(block1, block2, block3)
temprow <- c("Clase", "Número", "Mediana (dólares)", "Mediana (en dólares log)" ,"Media (en dólares log)", "Desv. estándar (en dólares log)") 
bigblock1 <- cbind (c(temprow,temprow, temprow), bigblock)
row.names(bigblock1) <- NULL

TableGen1(TableData=bigblock1 , 
         TextTitle='Estadísticas Resumidas de Reclamaciones de Automóviles por Clase de Riesgo', 
         Align='lrrrrrr', Digits=3, ColumnSpec=1:6,
         ColWidth = ColWidth4) %>%
       kableExtra::column_spec(1, width =  "6cm") 

library(HH)
AutoC   <- read.csv("CSVData/AutoClaims.csv", header=TRUE)
#  RECLAMACIONES DE AUTOMÓVILES
#  FIGURA 4.2

par(cex=0.6)
boxplot(log(PAID) ~ CLASS,cex=.6, cex.labels=2, data = AutoC,
        xlab = "", ylab = "")

Esta sección se centra en la clase de riesgo (CLASS) como la variable explicativa. Usamos la notación \(y_{ij}\) para referirnos a la \(i\)-ésima observación de la \(j\)-ésima clase de riesgo. Para la \(j\)-ésima clase de riesgo, asumimos que hay \(n_j\) observaciones. Existen \(n=n_1+n_2+\ldots +n_c\) observaciones en total. Los datos son:

\[ \begin{array}{cccccc} \small{\text{Datos para la clase de riesgo }}1 & \ \ \ \ & y_{11} & y_{21} & \ldots & y_{n_1,1} \\ \small{\text{Datos para la clase de riesgo }}2 & & y_{12} & y_{22} & \ldots & y_{n_2,1} \\ . & & . & . & \ldots & . \\ \small{\text{Datos para la clase de riesgo }} c & & y_{1c} & y_{2c} & \ldots & y_{n_c,c} \end{array} \]

donde \(c=18\) es el número de niveles del factor CLASS. Debido a que cada nivel de un factor puede organizarse en una sola fila (o columna), otro término para este tipo de datos es una “clasificación de una vía.” Así, un modelo de una vía es otro término para un modelo de un factor.

Una medida resumen importante para cada nivel del factor es el promedio de la muestra. Sea \[ \overline{y}_j=\frac{1}{n_j}\sum_{i=1}^{n_j}y_{ij} \] el promedio de la \(j\)-ésima CLASS.

Suposiciones del Modelo y Análisis

La ecuación del modelo ANOVA de un factor es \[ y_{ij}=\mu_j+ \varepsilon_{ij}\ \ \ \ \ \ i=1,\ldots ,n_j,\ \ \ \ \ j=1,\ldots ,c. \tag{4.7} \] Al igual que con los modelos de regresión, se asume que las desviaciones aleatorias \(\{\varepsilon_{ij} \}\) tienen una media cero con varianza constante (Suposición E3) y son independientes entre sí (Suposición E4). Dado que asumimos que el valor esperado de cada desviación es cero, tenemos \(\text{E}~y_{ij}=\mu_j\). Por lo tanto, interpretamos \(\mu_j\) como el valor esperado de la respuesta \(y_{ij}\), es decir, la media \(\mu\) varía según el nivel del factor \(j\).

Para estimar los parámetros \(\{\mu_j\}\), al igual que en la regresión, usamos el método de mínimos cuadrados, introducido en la Sección 2.1. Es decir, sea \(\mu^{\ast}_j\) una estimación “candidata” de \(\mu_j\). La cantidad \[ SS(\mu^{\ast}_1, \ldots , \mu^{\ast}_{c}) = \sum_{j=1}^{c} \sum_{i=1}^{n_j} (y_{ij}-\mu^{\ast}_j)^2 \] representa la suma de los cuadrados de las desviaciones de las respuestas respecto a estas estimaciones candidatas. A partir de algebra básica, el valor de \(\mu^{\ast}_j\) que minimiza esta suma de cuadrados es \(\bar{y}_j\). Por lo tanto, \(\bar{y}_j\) es la estimación por mínimos cuadrados de \(\mu_j\).

Para entender la confiabilidad de las estimaciones, podemos descomponer la variabilidad como en el caso de regresión, presentado en las Secciones 2.3.1 y 3.3. La suma mínima de los cuadrados de las desviaciones se llama suma de cuadrados del error y se define como \[ Error ~SS = SS(\bar{y}_1, \ldots, \bar{y}_{c}) = \sum_{j=1}^{c} \sum_{i=1}^{n_j} \left(y_{ij}-\bar{y}_j \right)^2. \] La variación total en el conjunto de datos se resume en la suma total de cuadrados, \[ Total ~SS=\sum_{j=1}^{c}\sum_{i=1}^{n_j}(y_{ij}-\bar{y})^2. \] La diferencia, llamada suma de cuadrados del factor, se puede expresar como: \[ \begin{array}{ll} Factor~ SS & = Total ~SS - Error ~SS \\ & = \sum_{j=1}^{c}\sum_{i=1}^{n_j}(y_{ij}-\bar{y})^2-\sum_{j=1}^{c}\sum_{i=1}^{n_j}(y_{ij}-\bar{y}_j)^2 = \sum_{j=1}^{c}\sum_{i=1}^{n_j}(\bar{y}_j-\bar{y})^2 \\ & = \sum_{j=1}^{c}n_j(\bar{y}_j-\bar{y})^2. \end{array} \] Las dos últimas igualdades se derivan de la manipulación algebraica. El \(Factor ~SS\) desempeña el mismo papel que el \(Regression ~SS\) en los Capítulos 2 y 3. La descomposición de la variabilidad se resume en la Tabla 4.6.

Tabla 4.6: Tabla ANOVA para el Modelo de Un Factor

Fuente	Suma de Cuadrados	\(df\)	Media Cuadrática
Factor	\(Factor ~SS\)	\(c-1\)	\(Factor ~MS\)
Error	\(Error ~SS\)	\(n-c\)	\(Error ~MS\)
Total	\(Total ~SS\)	\(n-1\)

Las convenciones para esta tabla son las mismas que en el caso de regresión. Es decir, la columna de media cuadrática (MS) se define dividiendo la columna de suma de cuadrados (SS) por la columna de grados de libertad (df). Por lo tanto, \(Factor~MS \equiv (Factor~SS)/(c-1)\) y \(Error~MS \equiv (Error~SS)/(n-c)\). Usamos \[ s^2 = \text{Error MS} = \frac{1}{n-c} \sum_{j=1}^{c}\sum_{i=1}^{n_j} e_{ij}^2 \] como nuestra estimación de \(\sigma^2\), donde \(e_{ij} = y_{ij} - \bar{y}_j\) es el residuo.

Con este valor de \(s\), se puede mostrar que el intervalo de estimación para \(\mu_j\) es \[ \bar{y}_j \pm t_{n-c,1-\alpha /2}\frac{s}{\sqrt{n_j}}. \tag{4.8} \]

Aquí, el valor t \(t_{n-c,1-\alpha /2}\) es un percentil de la distribución t con \(df=n-c\) grados de libertad.

---

Ejemplo: Reclamaciones de Automóviles - Continuación. Para ilustrar, la tabla ANOVA que resume el ajuste para los datos de reclamaciones de automóviles se presenta en la Tabla 4.7. Aquí, vemos que la media cuadrática del error es \(s^2 = 1.14.\)

Tabla 4.7: Tabla ANOVA para Reclamaciones de Automóviles Logarítmicas

Fuente	Suma de Cuadrados	\(df\)	Media Cuadrática
CLASS	39.2	17	2.31
Error	7729.0	6755	1.14
Total	7768.2	6772

En la tarificación de automóviles, se usan los promedios de las reclamaciones para ayudar a fijar los precios de las coberturas de seguros. Como ejemplo, para la CLASS C72, el promedio de la reclamación logarítmica es 7.183. A partir de la ecuación (4.8), un intervalo de confianza del 95% es \[ \small{ 7.183 \pm (1.96) \frac{\sqrt{1.14}}{\sqrt{85}} = 7.183 \pm 0.227 = (6.956 ,7.410). } \] Cabe destacar que estas estimaciones están en unidades logarítmicas naturales. En dólares, nuestra estimación puntual es \(e^{7.183} = 1,316.85\) y nuestro intervalo de confianza del 95% es \((e^{6.956} , e^{7.410}) \text{ o } (\$1,049.43, \$1,652.43)\).

---

Una característica importante de la descomposición y estimación en un ANOVA de un factor es la facilidad de cálculo. Aunque la suma de cuadrados parece compleja, es importante señalar que no se requieren cálculos matriciales. En cambio, todos los cálculos se pueden realizar mediante promedios y sumas de cuadrados. Esto ha sido un aspecto importante históricamente, antes de la era de la computación de escritorio disponible. Además, las aseguradoras pueden segmentar sus carteras en cientos o incluso miles de clases de riesgo en lugar de las 18 utilizadas en nuestros datos de Reclamaciones de Automóviles. Por lo tanto, incluso hoy en día puede ser útil identificar una variable categórica como un factor y dejar que su software estadístico utilice técnicas de estimación ANOVA. Además, la estimación ANOVA también proporciona una interpretación directa de los resultados.

Vínculo con la Regresión

Esta subsección muestra cómo un modelo ANOVA de un factor se puede reescribir como un modelo de regresión. Para ello, hemos visto que tanto el modelo de regresión como el modelo ANOVA de un factor utilizan una estructura de error lineal con las Suposiciones E3 y E4 para errores idénticamente y distribuidos de manera independiente. De manera similar, ambos utilizan la suposición de normalidad E5 para resultados de inferencia seleccionados (como intervalos de confianza). Ambos emplean variables explicativas no estocásticas como en la Suposición E2. Ambos tienen un término de error aditivo (media cero), por lo que la principal diferencia aparente está en la respuesta esperada, \(\mathrm{E }~y\).

Para el modelo de regresión lineal, \(\mathrm{E }~y\) es una combinación lineal de variables explicativas (Suposición F1). Para el modelo ANOVA de un factor, \(\mathrm{E}~y_] = \mu_j\) es una media que depende del nivel del factor. Para igualar estos dos enfoques, para el factor ANOVA con \(c\) niveles, definimos \(c\) variables binarias, \(x_1, x_2, \ldots, x_c\). Aquí, \(x_j\) indica si una observación cae o no en el nivel \(j\)-ésimo. Con estas variables, podemos reescribir nuestro modelo ANOVA de un factor como \[ y = \mu_1 x_1 + \mu_2 x_2 + \ldots + \mu_c x_c + \varepsilon. \tag{4.9} \] Así, hemos reescrito la respuesta esperada del ANOVA de un factor como una función de regresión, aunque utilizando una forma sin intercepto (como en la ecuación (3.5)).

El ANOVA de un factor es un caso especial de nuestro modelo de regresión habitual, utilizando variables binarias del factor como variables explicativas en la función de regresión. Como hemos visto, no se necesitan cálculos matriciales para la estimación por mínimos cuadrados. Sin embargo, siempre se pueden utilizar los procedimientos matriciales desarrollados en el Capítulo 3. La Sección 4.7.1 muestra cómo nuestra expresión matricial habitual para los coeficientes de regresión (\(\mathbf{b} = \left(\mathbf{X}^{\prime}\mathbf{X}\right)^{-1}\mathbf{X}^{\prime}\mathbf{y}\)) se reduce a las estimaciones simples \(\bar{y}_j\) cuando se utiliza una sola variable categórica.

Reparametrización

Para incluir un término de intercepto, definimos \(\tau_j = \mu_j - \mu\), donde \(\mu\) es un parámetro aún no especificado. Como cada observación debe pertenecer a una de las \(c\) categorías, tenemos que \(x_1 + x_2 + \ldots + x_{c} = 1\) para cada observación. Así, al usar \(\mu_j = \tau_j + \mu\) en la ecuación (4.9), obtenemos \[ y = \mu + \tau_1 x_1 + \tau_2 x_2 + \ldots + \tau_{c} x_{c} + \varepsilon, \tag{4.10} \] Así, hemos reescrito el modelo en lo que parece ser nuestro formato usual de regresión.

Usamos \(\tau\) en lugar de \(\beta\) por razones históricas. Los modelos ANOVA fueron inventados por R.A. Fisher en relación con experimentos agrícolas. Aquí, la configuración típica es aplicar varios tratamientos a parcelas de tierra para cuantificar las respuestas de rendimiento de los cultivos. Así, la letra griega “t”, \(\tau\), sugiere la palabra tratamiento, otro término utilizado para describir los niveles del factor de interés.

Una versión más simple de la ecuación (4.10) se puede dar cuando identificamos el nivel del factor. Es decir, si sabemos que una observación pertenece al nivel \(j\)-ésimo, entonces solo \(x_j\) es uno y los otros \(x\) son 0. Por lo tanto, una expresión más simple de la ecuación (4.10) es \[ y_{ij} = \mu + \tau_j + \varepsilon_{ij}. \]

Al comparar las ecuaciones (4.9) y (4.10), vemos que el número de parámetros ha aumentado en uno. Es decir, en la ecuación (4.9) hay \(c\) parámetros, \(\mu_1, \ldots, \mu_c\), mientras que en la ecuación (4.10) hay \(c + 1\) parámetros, \(\mu\) y \(\tau_1, \ldots, \tau_c\). Se dice que el modelo en la ecuación (4.10) está sobreparametrizado. Es posible estimar este modelo directamente, utilizando la teoría general de modelos lineales, resumida en la Sección 4.7.3. En esta teoría, los coeficientes de regresión no necesitan ser identificables. Alternativamente, se pueden hacer equivalentes estas dos expresiones restringiendo el movimiento de los parámetros en la ecuación (4.10). A continuación, presentamos dos formas de imponer restricciones.

El primer tipo de restricción, generalmente utilizado en el contexto de regresión, es requerir que uno de los \(\tau\) sea cero. Esto equivale a eliminar una de las variables explicativas. Por ejemplo, podríamos usar \[ y = \mu + \tau_1 x_1 + \tau_2 x_2 + \ldots + \tau_{c-1} x_{c-1} + \varepsilon, \tag{4.11} \] eliminando \(x_c\). Con esta formulación, es fácil ajustar el modelo en la ecuación (4.11) utilizando rutinas de software de regresión, porque solo se necesita ejecutar la regresión con \(c-1\) variables explicativas. Sin embargo, se debe tener cuidado con la interpretación de los parámetros. Para igualar los modelos en las ecuaciones (4.9) y (4.10), necesitamos definir \(\mu \equiv \mu_c\) y \(\tau_j = \mu_j - \mu_c\) para \(j=1,2,\ldots,c-1\). Es decir, el término de intercepto de la regresión es el nivel medio de la categoría eliminada, y cada coeficiente de regresión es la diferencia entre un nivel medio y el nivel medio eliminado. No es necesario eliminar el último nivel \(c\), y de hecho, se podría eliminar cualquier nivel. Sin embargo, la interpretación de los parámetros depende de la variable eliminada. Con esta restricción, los valores ajustados son \(\hat{\mu} = \hat{\mu}_c = \bar{y}_c\) y \(\hat{\tau}_j = \hat{\mu}_j - \hat{\mu}_c = \bar{y}_j - \bar{y}_c.\) Recordemos que el símbolo de sombrero (\(\hat{\cdot}\)), o “hat,” representa un valor estimado o ajustado.

El segundo tipo de restricción es interpretar \(\mu\) como una media para toda la población. Para ello, el requisito usual es \(\mu \equiv \frac{1}{n} \sum_{j=1}^c n_j \mu_j\), es decir, \(\mu\) es un promedio ponderado de medias. Con esta definición, interpretamos \(\tau_j = \mu_j - \mu\) como diferencias de tratamiento entre un nivel medio y la media poblacional. Otra forma de expresar esta restricción es \(\sum_{j=1}^{c} n_j \tau_j = 0\), es decir, la suma (ponderada) de las diferencias de tratamiento es cero. La desventaja de esta restricción es que no se puede implementar fácilmente con una rutina de regresión, y se necesita una rutina especial. La ventaja es que hay una simetría en las definiciones de los parámetros. No es necesario preocuparse por qué variable se está eliminando de la ecuación, lo cual es una consideración importante. Con esta restricción, los valores ajustados son \[ \hat{\mu} = \frac{1}{n} \sum_{j=1}^{c} n_j \hat{\mu}_j = \frac{1}{n} \sum_{j=1}^{c} n_j \bar{y}_j = \bar{y} \] y \[ \hat{\tau}_j = \hat{\mu}_j - \hat{\mu} = \bar{y}_j - \bar{y}. \]

4.4 Combinando Variables Explicativas Categóricas y Continuas

Existen varias formas de combinar variables explicativas categóricas y continuas. Inicialmente, presentamos el caso de solo una variable categórica y una variable continua. Luego, presentamos brevemente el caso general, llamado modelo lineal general. Cuando se combinan modelos de variables categóricas y continuas, usamos la terminología factor para la variable categórica y covariable para la variable continua.

Combinando un Factor y una Covariable

Comencemos con los modelos más simples que utilizan un factor y una covariable. En la Sección 4.3, introdujimos el modelo de un solo factor \(y_{ij} = \mu_j + \varepsilon_{ij}\). En el Capítulo 2, introdujimos la regresión lineal básica en términos de una variable continua, o covariable, usando \(y_{ij} = \beta_0 + \beta_1 x_{ij} + \varepsilon_{ij}\). La Tabla 4.8 resume diferentes enfoques que podrían usarse para representar combinaciones de un factor y una covariable.

Tabla 4.8: Varios Modelos que Representan Combinaciones de Un Factor y Una Covariable

Descripción del Modelo	Notación
ANOVA de un factor (modelo sin covariable)	\(y_{ij} = \mu_j + \varepsilon_{ij}\)
Regresión con intercepto y pendiente constante (modelo sin factor)	\(y_{ij} = \beta_0 + \beta_1 x_{ij} + \varepsilon_{ij}\)
Regresión con intercepto variable y pendiente constante (modelo de análisis de covarianza)	\(y_{ij} = \beta_{0j} + \beta_1 x_{ij} + \varepsilon_{ij}\)
Regresión con intercepto constante y pendiente variable	\(y_{ij} = \beta_0 + \beta_{1j} x_{ij} + \varepsilon_{ij}\)
Regresión con intercepto y pendiente variable	\(y_{ij} = \beta_{0j} + \beta_{1j} x_{ij} + \varepsilon_{ij}\)

Podemos interpretar la regresión con intercepto variable y pendiente constante como un modelo aditivo, porque estamos sumando el efecto del factor, \(\beta_{0j}\), al efecto de la covariable, \(\beta_1 x_{ij}\). Nótese que también se podría usar la notación \(\mu_j\) en lugar de \(\beta_{0j}\) para sugerir la presencia de un efecto de factor. Este también es conocido como un modelo de análisis de covarianza (ANCOVA). La regresión con intercepto y pendiente variables puede considerarse un modelo de interacción. Aquí, tanto el intercepto, \(\beta_{0j}\), como la pendiente, \(\beta_{1j}\), pueden variar según el nivel del factor. En este sentido, interpretamos que el factor y la covariable están “interactuando”. El modelo con intercepto constante y pendiente variable típicamente no se usa en la práctica; se incluye aquí por completitud. Con este modelo, el factor y la covariable interactúan solo a través de la pendiente variable. Las Figuras 4.3, 4.4 y 4.5 ilustran las respuestas esperadas de estos modelos.

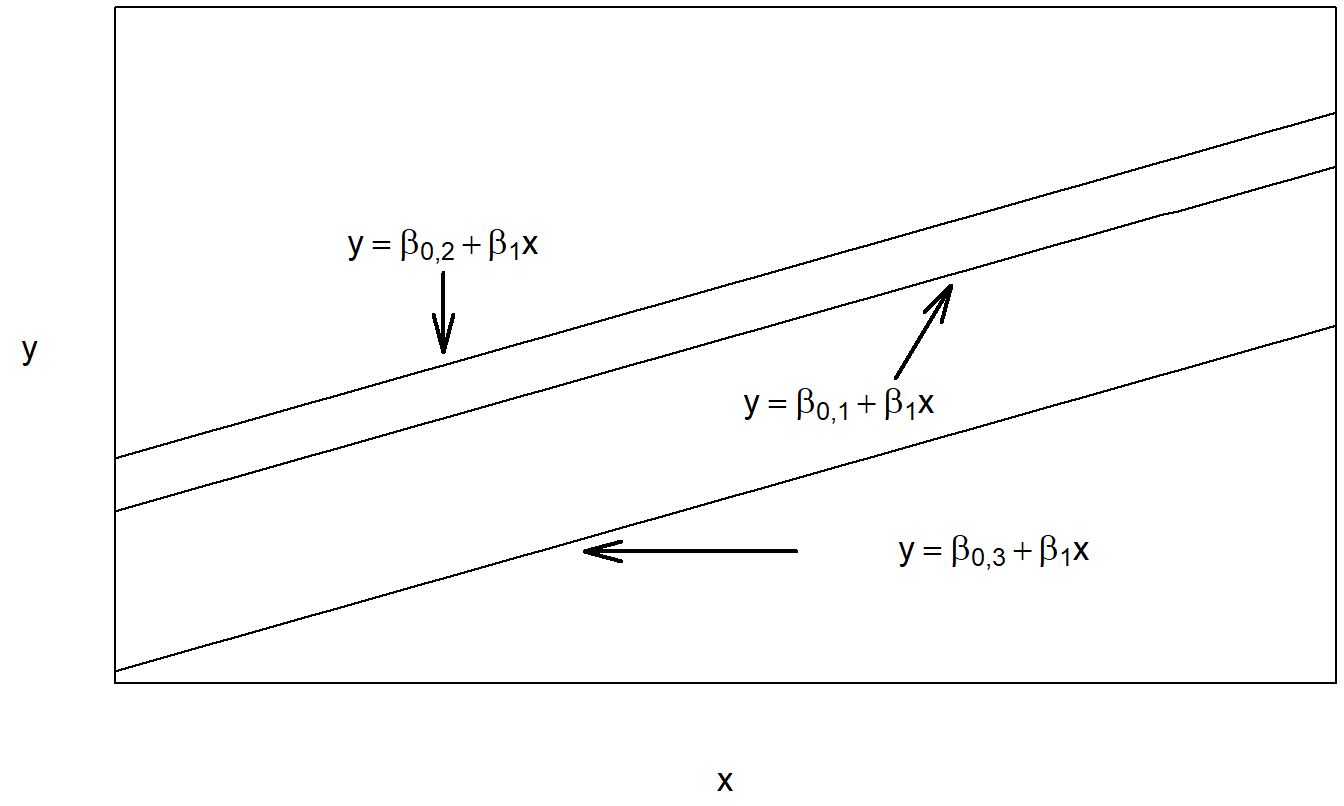
Figura 4.3: Gráfico de la respuesta esperada frente a la covariable para el modelo de regresión con intercepto variable y pendiente constante.

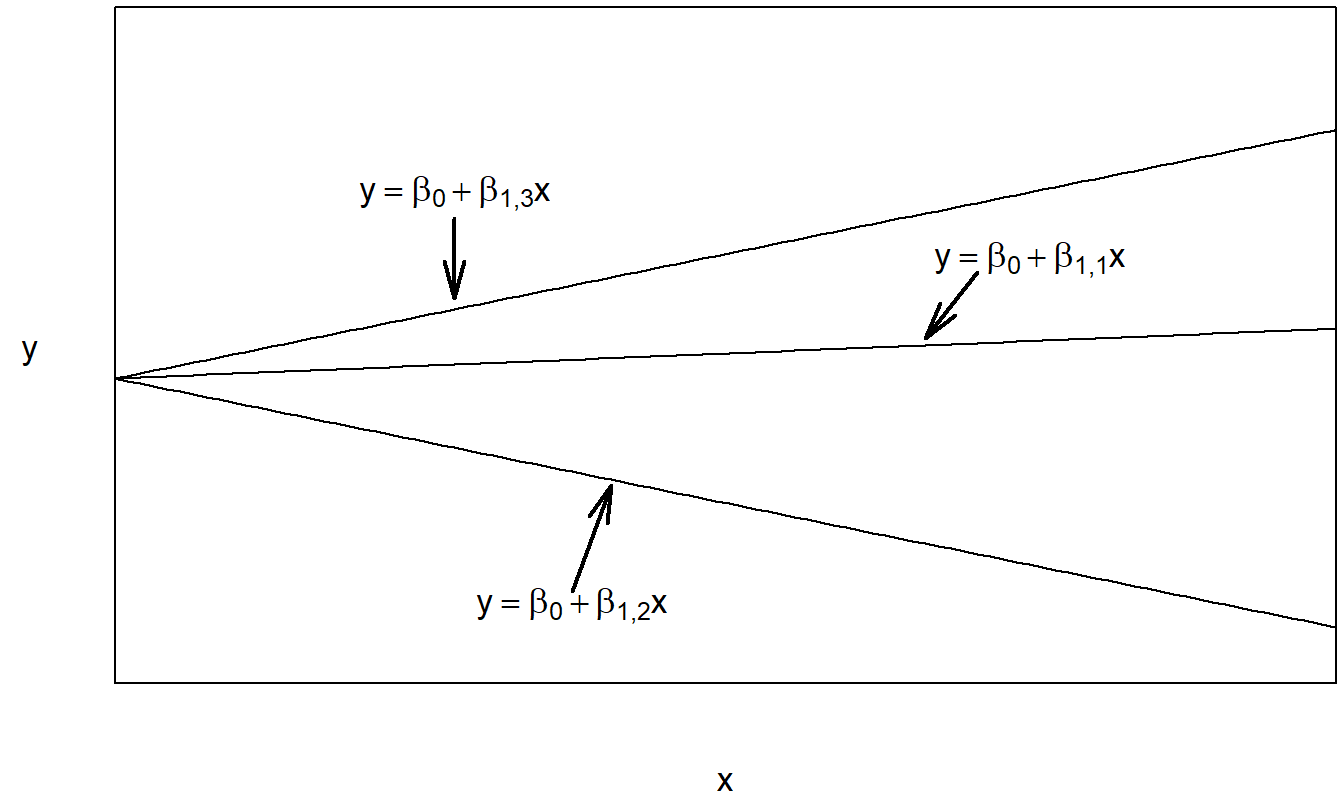
Figura 4.4: Gráfico de la respuesta esperada frente a la covariable para el modelo de regresión con intercepto constante y pendiente variable.

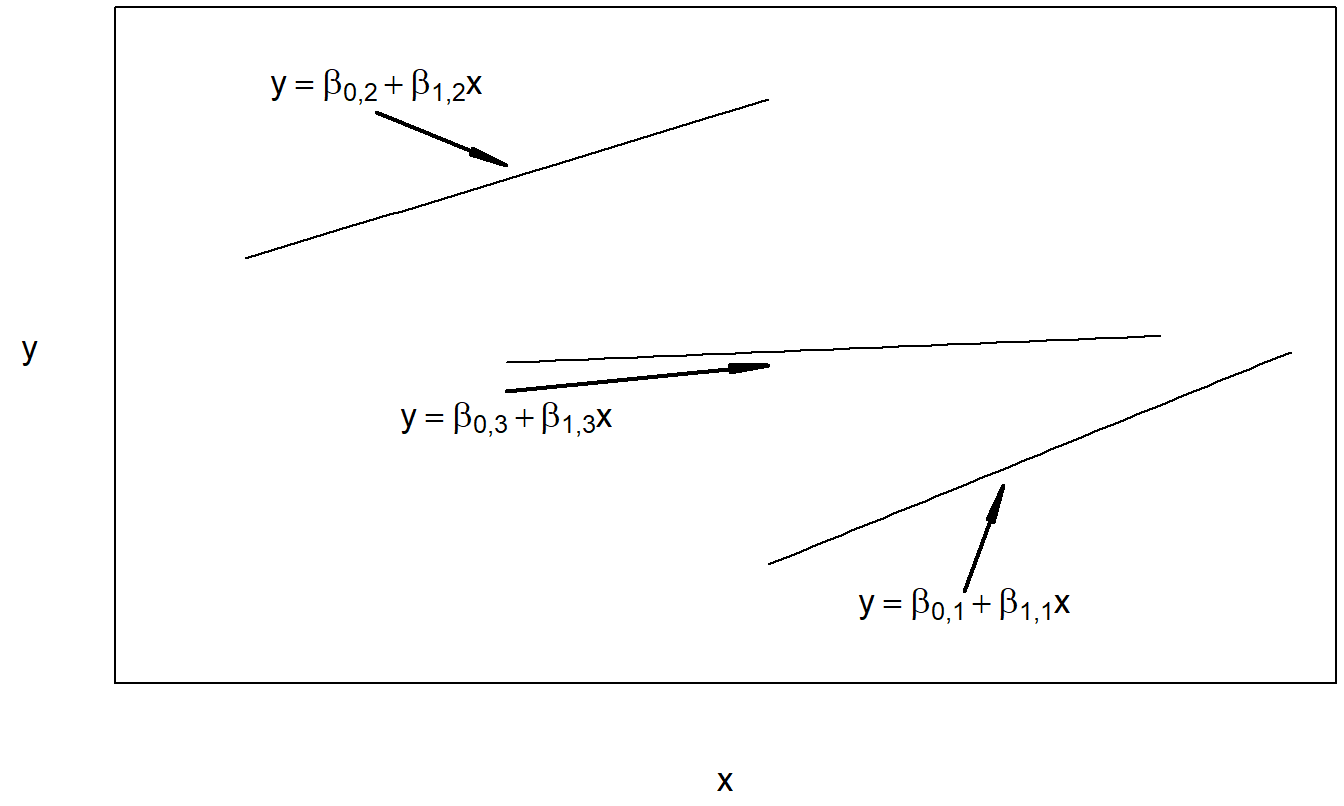
Figura 4.5: Gráfico de la respuesta esperada frente a la covariable para el modelo de regresión con intercepto variable y pendiente variable.

Código R para Producir las Figuras 4.3, 4.4, y 4.5

## Figura 4.3 
x <- seq(0, 100, length = 101)
y <- 0.15 * x

par(mar = c(3.2, 3, .2, .2))
plot(x, y, type = "l", xlim = c(10, 90), xaxt = "n", ylim = c(1.5, 25), yaxt = "n", 
       ylab = "", xlab = "")
mtext("y", side = 2, las = 1, line = 2, cex = 1.1)
mtext("x", side = 1, line = 2, cex = 1.1)
lines(x, y + 6)
lines(x, y + 8)
arrows(40, 5.5, 55, 5.5, code = 1, lwd = 2, angle = 15, length = 0.2)
text(69, 5.5, expression(y == beta["0,3"] + beta[1] * x), cex = 1.1)
arrows(30, 13, 30, 16, code = 1, lwd = 2, angle = 15, length = 0.2)
text(30, 17, expression(y == beta["0,2"] + beta[1] * x), cex = 1.1)
arrows(66, 15.5, 62, 12, code = 1, lwd = 2, angle = 15, length = 0.2)
text(58, 11, expression(y == beta["0,1"] + beta[1] * x), cex = 1.1)

## Figura 4.4 
x <- seq(0, 100, length = 101)
y3 <- 12 + 0.1 * x
y2 <- 12 - 0.1 * x
y1 <- 12 + 0.02 * x

par(mar = c(3.2, 3, .2, .2))
plot(x, y1, type = "l", xlim = c(3.5, 90), xaxt = "n", ylim = c(1.5, 25), yaxt = "n", ylab = "", xlab = "")
mtext("y", side = 2, las = 1, line = 2, cex = 1.1)
mtext("x", side = 1, line = 2, cex = 1.1)
lines(x, y2)
lines(x, y3)

arrows(38, 8, 35, 4, code = 1, lwd = 2, angle = 15, length = 0.2)
text(35, 3.5, expression(y == beta[0] + beta["1,2"] * x), cex = 1.1)
arrows(26, 15, 26, 18, code = 1, lwd = 2, angle = 15, length = 0.2)
text(26, 19, expression(y == beta[0] + beta["1,3"] * x), cex = 1.1)
arrows(62, 13.5, 66, 16, code = 1, lwd = 2, angle = 15, length = 0.2)
text(70, 16.5, expression(y == beta[0] + beta["1,1"] * x), cex = 1.1)

## Figura 4.5 

x1 <- seq(50, 90, length = 51)
y1 <- -5 + 0.2 * x1
x2 <- seq(30, 80, length = 41)
y2 <- 12 + 0.02 * x2
x3 <- seq(10, 50, length = 41)
y3 <- 15 + 0.15 * x3

par(mar = c(3.2, 3, .2, .2))
plot(x1, y1, type = "l", xlim = c(3.5, 90), xaxt = "n",
   ylim = c(1.5, 25), ylab = "", xlab = "", yaxt = "n")
mtext("y", side = 2, las = 1, line = 2, cex = 1.1)
mtext("x", side = 1, line = 2, cex = 1.1)
lines(x2, y2)
lines(x3, y3)

arrows(68, 8, 65, 4, code = 1, lwd = 2, angle = 5, length = 0.2)
text(65, 3.5, expression(y == beta["0,1"] + beta["1,1"] * x), cex = 1.1)
arrows(50, 12.5, 30, 11.5, code = 1, lwd = 2, angle = 5, length = 0.2)
text(30, 10.5, expression(y == beta["0,3"] + beta["1,3"] * x), cex = 1.1)
arrows(30, 20, 20, 22, code = 1, lwd = 2, angle = 5, length = 0.2)
text(20, 23, expression(y == beta["0,2"] + beta["1,2"] * x), cex = 1.1)

Para cada modelo presentado en la Tabla 4.8, las estimaciones de los parámetros pueden calcularse utilizando el método de mínimos cuadrados. Como es habitual, esto significa escribir la respuesta esperada, \(\mathrm{E }~y_{ij}\), como una función de variables conocidas y parámetros desconocidos. Para el modelo de regresión con intercepto variable y pendiente constante, las estimaciones de mínimos cuadrados pueden expresarse de manera compacta como:

\[ b_1 = \frac{\sum_{j=1}^{c}\sum_{i=1}^{n_j} (x_{ij} - \bar{x}_j) (y_{ij} - \bar{y}_j)}{\sum_{j=1}^{c}\sum_{i=1}^{n_j} (x_{ij} - \bar{x}_j)^2} \]

y \(b_{0j} = \bar{y}_j - b_1 \bar{x}_j\). De manera similar, las estimaciones de mínimos cuadrados para el modelo de regresión con intercepto y pendiente variables pueden expresarse como:

\[ b_{1j} = \frac{\sum_{i=1}^{n_j} (x_{ij} - \bar{x}_j) (y_{ij} - \bar{y}_j)}{\sum_{i=1}^{n_j} (x_{ij} - \bar{x}_j)^2} \]

y \(b_{0j} = \bar{y}_j - b_{1j} \bar{x}_j\). Con estas estimaciones de los parámetros, se pueden calcular los valores ajustados.

Para cada modelo, los valores ajustados se definen como la respuesta esperada con los parámetros desconocidos reemplazados por sus estimaciones de mínimos cuadrados. Por ejemplo, para el modelo de regresión con intercepto variable y pendiente constante, los valores ajustados son \(\hat{y}_{ij} = b_{0j} + b_1 x_{ij}.\)

---

Ejemplo: Costos Hospitalarios en Wisconsin. Ahora estudiamos el impacto de varios predictores en los costos hospitalarios en el estado de Wisconsin. Identificar predictores de los costos hospitalarios puede proporcionar dirección a los hospitales, al gobierno, a las aseguradoras y a los consumidores en el control de estas variables, lo que a su vez lleva a un mejor control de los costos hospitalarios. Los datos para el año 1989 fueron obtenidos de la Oficina de Información de Salud, del Departamento de Salud y Servicios Humanos de Wisconsin. Se utilizan datos transversales, que detallan los costos de alta de 20 grupos relacionados con el diagnóstico (DRG) para hospitales en el estado de Wisconsin, desglosados en nueve áreas principales de servicios de salud y tres tipos de pagador (Pago por servicio, HMO y otros). Aunque hay 540 combinaciones potenciales de DRG, área y pagador (\(20 \times 9 \times 3 = 540\)), solo 526 combinaciones se realizaron realmente en el conjunto de datos de 1989. Otros predictores incluidos fueron el logaritmo del número total de altas (NO DSCHG) y el número total de camas hospitalarias (NUM BEDS) para cada combinación. La variable de respuesta es el logaritmo de los costos hospitalarios totales por número de altas (CHGNUM). Para simplificar la presentación, ahora consideramos solo los costos asociados con tres grupos relacionados con el diagnóstico (DRG): DRG #209, DRG #391, y DRG #430.

La covariable, \(x\), es el logaritmo natural del número de altas. En entornos ideales, los hospitales con más pacientes disfrutan de menores costos debido a economías de escala. En entornos no ideales, los hospitales pueden no tener capacidad excedente y, por lo tanto, los hospitales con más pacientes tienen costos más altos. Uno de los propósitos de este análisis es investigar la relación entre los costos hospitalarios y la utilización hospitalaria.

Recuerde que nuestra medida de los costos hospitalarios es el logaritmo de los costos por alta (\(y\)). El diagrama de dispersión en la Figura 4.6 da una idea preliminar de la relación entre \(y\) y \(x\). Notamos que parece haber una relación negativa entre \(y\) y \(x\).

La relación negativa entre \(y\) y \(x\) sugerida por la Figura 4.6 es engañosa y está inducida por una variable omitida, la categoría del costo (DRG). Para ver el efecto conjunto de la variable categórica DRG y la variable continua \(x\), en la Figura 4.7 se muestra un gráfico de \(y\) versus \(x\) donde los símbolos de trazado son códigos para el nivel de la variable categórica. En este gráfico, vemos que el nivel de costo varía según el nivel del factor DRG. Además, para cada nivel de DRG, la pendiente entre \(y\) y \(x\) es cero o positiva. Las pendientes no son negativas, como sugiere la Figura 4.6.

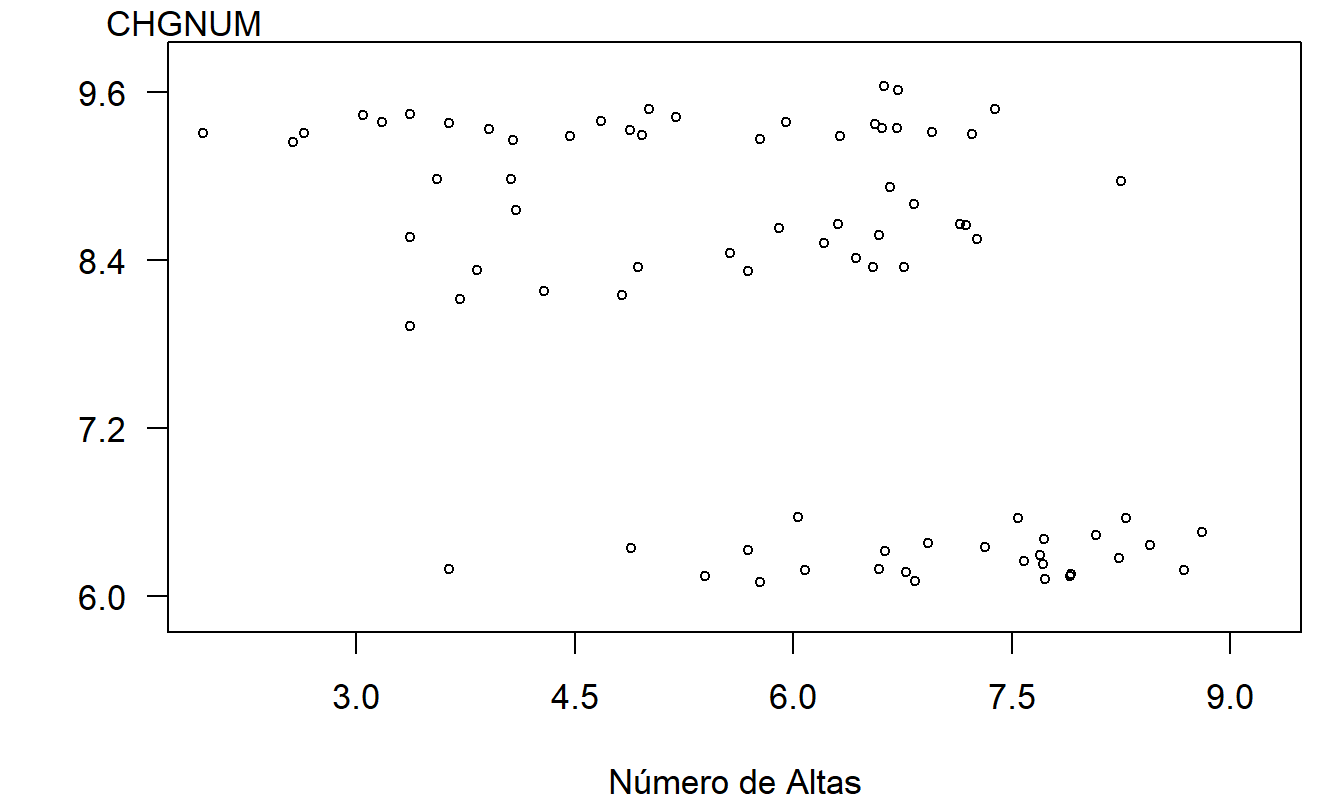
Figura 4.6: Gráfico del logaritmo natural del costo por alta versus logaritmo natural del número de altas. Este gráfico sugiere una relación negativa engañosa.

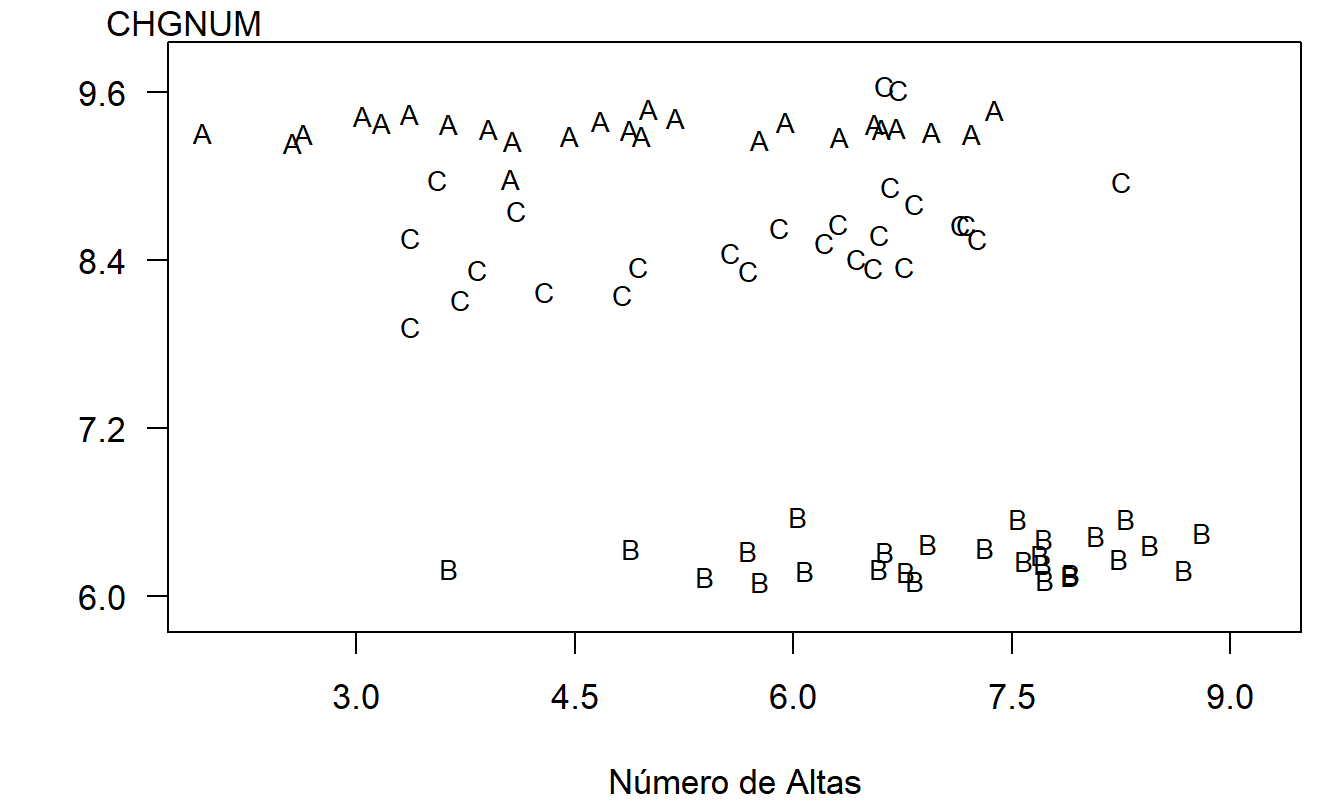
Figura 4.7: Gráfico con letras del logaritmo natural del costo por alta versus logaritmo natural del número de altas según DRG. Aquí, A es para DRG #209, B es para DRG #391, y C es para DRG #430.

Código R para Producir las Figuras 4.6 y 4.7

## C5_HOSP.txt

HospitalCosts    <- read.csv("CSVData/WiscHospCosts.csv", header=TRUE)
# attach(HospitalCosts)
# LNCHGNUM<-log(CHG_NUM)
## Figura 4.6
par(mar=c(4.1,4,1,1), cex=1.1)
plot(log(CHG_NUM) ~ log(NO_DSCHG), data=HospitalCosts,
     subset=DRG==209|DRG==391|DRG==430,type="p",pch=1,cex=0.6, 
     xlim=c(2,9.2),xaxp=c(1.5,9,5),xlab="Número de Altas",ylim=c(5.9,9.8),
     yaxp=c(6.0,9.6,3),ylab="",las=1)
mtext("CHGNUM", side=2, at=10.1, las=1, cex=1.1, adj=.4)

## Figura 4.7
DRGabc<-character(length=length(HospitalCosts$DRG))
for (i in 1:length(HospitalCosts$DRG))
{DRGabc[i]<-if (HospitalCosts$DRG[i]==209) "A" else if (HospitalCosts$DRG[i]==391) 
    "B" else if (HospitalCosts$DRG[i]==430) "C" else "D"}

par(mar=c(4.1,4,1,1), cex=1.1)
plot(log(CHG_NUM) ~ log(NO_DSCHG), data=HospitalCosts,
    subset=DRG==209|DRG==391|DRG==430,type="p",
    pch=as.character(DRGabc),cex=0.8, xlim=c(2,9.2),
    xaxp=c(1.5,9,5),xlab="Número de Altas",ylim=c(5.9,9.8),
    yaxp=c(6.0,9.6,3),ylab="",las=1)
mtext("CHGNUM", side=2, at=10.1, las=1, cex=1.1, adj=.4)

Tabla 4.9: Bondad de Ajuste de los Modelos de Costos Hospitalarios en Wisconsin

Descripción del Modelo	Grados de libertad del modelo	Grados de libertad del error	Suma de cuadrados del error	R-cuadrado (%)	Media Cuadrática
ANOVA de un factor	2	76	9.396	93.3	0.124
Regresión con intercepto y pendiente constantes	1	77	115.059	18.2	1.222
Regresión con intercepto variable y pendiente constante	3	75	7.482	94.7	0.100
Regresión con intercepto constante y pendiente variable	3	75	14.048	90.0	0.187
Regresión con intercepto y pendiente variables	5	73	5.458	96.1	0.075

Cada uno de los cinco modelos definidos en la Tabla 4.8 fue ajustado a este subconjunto del estudio de caso hospitalario. Las estadísticas resumen se encuentran en la Tabla 4.9. Para este conjunto de datos, hay \(n = 79\) observaciones y \(c = 3\) niveles del factor DRG. Para cada modelo, los grados de libertad del modelo son el número de parámetros del modelo menos uno. Los grados de libertad del error son el número de observaciones menos el número de parámetros del modelo.

Usando variables binarias, cada uno de los modelos en la Tabla 4.8 puede escribirse en un formato de regresión. Como hemos visto en la Sección 4.2, cuando un modelo puede escribirse como un subconjunto de otro modelo más grande, tenemos procedimientos formales de prueba disponibles para decidir cuál modelo es más apropiado. Para ilustrar este procedimiento de prueba con nuestro ejemplo de DRG, a partir de la Tabla 4.9 y los gráficos asociados, parece claro que el factor DRG es importante. Además, una prueba \(t\), que no se presenta aquí, muestra que la covariable \(x\) es importante. Por lo tanto, comparemos el modelo completo \(\mathrm{E}~y_{ij} = \beta_{0,j} + \beta_{1,j}x\) con el modelo reducido \(\mathrm{E}~y_{ij} = \beta_{0,j} + \beta_1x\). En otras palabras, ¿hay una pendiente diferente para cada DRG?

Usando la notación de la Sección 4.2, llamamos al intercepto y la pendiente variables el modelo completo. Bajo la hipótesis nula, \(H_0: \beta_{1,1} = \beta_{1,2} = \beta_{1,3}\), obtenemos el modelo con intercepto variable y pendiente constante. Así, usando el cociente \(F\) en la ecuación (4.2), tenemos:

\[ \small{ F\text{-ratio} = \frac{(Error~SS)_{reduced} - (Error~SS)_{full}}{ps_{full}^2} = \frac{7.482 - 5.458}{2 \times 0.075} = 13.535. } \]

El percentil 95 de la distribución \(F\) con \(df_1 = p = 2\) y \(df_2 = (df)_{full} = 73\) es aproximadamente 3.13. Por lo tanto, esta prueba nos lleva a rechazar la hipótesis nula y a declarar válida la alternativa, el modelo de regresión con intercepto variable y pendiente variable.

---

Combinación de Dos Factores

Hemos visto cómo combinar covariables, así como una covariable y un factor, tanto de manera aditiva como con interacciones. De la misma manera, supongamos que tenemos dos factores, como sexo (dos niveles: masculino/femenino) y edad (tres niveles: joven/mediana/anciana). Las variables binarias correspondientes serían \(x_1\) para indicar si la observación representa a una mujer, \(x_2\) para indicar si la observación representa a una persona joven, y \(x_3\) para indicar si la observación representa a una persona de mediana edad.

Un modelo aditivo para estos dos factores puede usar la función de regresión

\[ \mathrm{E }~y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3. \]

Como hemos visto, este modelo es sencillo de interpretar. Por ejemplo, podemos interpretar \(\beta_1\) como el efecto del sexo, manteniendo constante la edad.

También podemos incorporar dos términos de interacción, \(x_1 x_2\) y \(x_1 x_3\). Usando las cinco variables explicativas, obtenemos la función de regresión

\[ \mathrm{E }~y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + \beta_4 x_1 x_2 + \beta_5 x_1 x_3. \tag{4.12} \]

Aquí, las variables \(x_1\), \(x_2\), y \(x_3\) se conocen como los efectos principales. La Tabla 4.10 ayuda a interpretar esta ecuación. Específicamente, hay seis tipos de personas que podríamos encontrar: hombres y mujeres que son jóvenes, de mediana edad o ancianos. Tenemos seis parámetros en la ecuación (4.12). La Tabla 4.10 proporciona el enlace entre los parámetros y los tipos de personas. Al usar los términos de interacción, no imponemos ninguna especificación previa sobre los efectos aditivos de cada factor. De la Tabla 4.10, vemos que la interpretación de los coeficientes de regresión en la ecuación (4.12) no es directa. Sin embargo, usar el modelo aditivo con términos de interacción es equivalente a crear una nueva variable categórica con seis niveles, uno para cada tipo de persona. Si los términos de interacción son críticos en su estudio, puede ser conveniente crear un nuevo factor que incorpore los términos de interacción simplemente para facilitar la interpretación.

Tabla 4.10: Función de Regresión para un Modelo de Dos Factores con Interacciones

Sexo	Edad	\(x_1\)	\(x_2\)	\(x_3\)	\(x_4\)	\(x_5\)	Función de Regresión
Masculino	Joven	0	1	0	0	0	\(\beta_0 + \beta_2\)
Masculino	Mediana	0	0	1	0	0	\(\beta_0 + \beta_3\)
Masculino	Anciana	0	0	0	0	0	\(\beta_0\)
Femenino	Joven	1	1	0	1	0	\(\beta_0 + \beta_1 + \beta_2 + \beta_4\)
Femenino	Mediana	1	0	1	0	1	\(\beta_0 + \beta_1 + \beta_3 + \beta_5\)
Femenino	Anciana	1	0	0	0	0	\(\beta_0 + \beta_1\)

Las extensiones a más de dos factores siguen de manera similar. Por ejemplo, supongamos que está examinando el comportamiento de empresas con sede en diez regiones geográficas, dos estructuras organizativas (con fines de lucro versus sin fines de lucro) con cuatro años de datos. Si decide tratar cada variable como un factor y desea modelar todos los términos de interacción, entonces esto es equivalente a un factor con \(10 \times 2 \times 4 = 80\) niveles. Los modelos con términos de interacción pueden tener un número considerable de parámetros y el analista debe ser prudente al especificar las interacciones a considerar.

Modelo Lineal General

El modelo lineal general extiende el modelo de regresión lineal de dos maneras. Primero, las variables explicativas pueden ser continuas, categóricas o una combinación. La única restricción es que entren linealmente de tal manera que la función de regresión resultante

\[ \mathrm{E}~y = \beta_0 + \beta_1 x_1 + \ldots + \beta_k x_k \tag{4.13} \]

sea una combinación lineal de coeficientes. Como hemos visto, podemos elevar al cuadrado las variables continuas o tomar otras transformaciones no lineales (como logaritmos) así como usar variables binarias para representar variables categóricas, por lo que esta “restricción”, como su nombre lo indica, permite una amplia clase de funciones generales para representar los datos.

La segunda extensión es que las variables explicativas pueden ser combinaciones lineales unas de otras en el modelo lineal general. Debido a esto, en el caso del modelo lineal general, las estimaciones de los parámetros no tienen por qué ser únicas. Sin embargo, una característica importante del modelo lineal general es que los valores ajustados resultantes resultan ser únicos, utilizando el método de mínimos cuadrados.

Por ejemplo, en la Sección 4.3 vimos que el modelo ANOVA de un factor podía expresarse como un modelo de regresión con \(c\) variables indicadoras. Sin embargo, si hubiéramos intentado estimar el modelo en la ecuación (4.10), el método de mínimos cuadrados no habría llegado a un conjunto único de estimaciones de los coeficientes de regresión. La razón es que, en la ecuación (4.10), cada variable explicativa puede expresarse como una combinación lineal de las otras. Por ejemplo, observe que \(x_c = 1 - (x_1 + x_2 + \ldots + x_{c-1})\).

El hecho de que las estimaciones de los parámetros no sean únicas es una desventaja, pero no una insuperable. La suposición de que las variables explicativas no sean combinaciones lineales unas de otras significa que podemos calcular estimaciones únicas de los coeficientes de regresión utilizando el método de mínimos cuadrados. En términos de matrices, porque las variables explicativas no son combinaciones lineales unas de otras, la matriz \(\mathbf{X}^{\prime}\mathbf{X}\) no es invertible.

Específicamente, supongamos que estamos considerando la función de regresión en la ecuación (4.13) y, utilizando el método de mínimos cuadrados, nuestras estimaciones de los coeficientes de regresión son \(b_0^{o}, b_1^{o}, \ldots, b_k^{o}\). Este conjunto de estimaciones de los coeficientes de regresión minimiza nuestra suma de cuadrados de los errores, pero puede haber otros conjuntos de coeficientes que también minimicen la suma de cuadrados de los errores. Los valores ajustados se calculan como \(\hat{y}_i = b_0^{o} + b_1^{o} x_{i1} + \ldots + b_k^{o} x_{ik}\). Se puede demostrar que los valores ajustados resultantes son únicos, en el sentido de que cualquier conjunto de coeficientes que minimice la suma de cuadrados de los errores produce los mismos valores ajustados (ver Sección 4.7.3).

Por lo tanto, para un conjunto de datos y un modelo lineal general especificado, los valores ajustados son únicos. Debido a que los residuos se calculan como las respuestas observadas menos los valores ajustados, tenemos que los residuos son únicos. Debido a que los residuos son únicos, tenemos que las sumas de cuadrados de los errores son únicas. Por lo tanto, parece razonable, y es cierto, que podemos usar la prueba general de hipótesis descrita en la Sección 4.2 para decidir si las colecciones de variables explicativas son importantes.

En resumen, para los modelos lineales generales, las estimaciones de los parámetros pueden no ser únicas y, por lo tanto, no significativas. Una parte importante de los modelos de regresión es la interpretación de los coeficientes de regresión. Esta interpretación no está necesariamente disponible en el contexto del modelo lineal general. Sin embargo, para los modelos lineales generales, todavía podemos discutir la importancia de una variable individual o colección de variables a través de pruebas parciales F. Además, los valores ajustados, y el correspondiente ejercicio de predicción, funcionan en el contexto del modelo lineal general. La ventaja del contexto del modelo lineal general es que no necesitamos preocuparnos por el tipo de restricciones a imponer en los parámetros. Aunque no es el tema de este texto, esta ventaja es particularmente importante en los diseños experimentales complicados utilizados en las ciencias de la vida. El lector encontrará que las rutinas de estimación del modelo lineal general están ampliamente disponibles en los paquetes de software estadístico disponibles en el mercado hoy en día.

4.5 Lecturas Adicionales y Referencias

Hay varios buenos libros sobre modelos lineales que se enfocan en variables categóricas y técnicas de análisis de variables. Hocking (2003) y Searle (1987) son buenos ejemplos.

Referencias del Capítulo

• Hocking, Ronald R. (2003). Methods and Applications of Linear Models: Regression and the Analysis of Variance John Wiley and Sons, New York.
• Keeler, Emmett B., and John E. Rolph (1988). The demand for episodes of treatment in the Health Insurance Experiment. Journal of Health Economics 7: 337-367.
• Searle, Shayle R. (1987). Linear Models for Unbalanced Data. John Wiley & Sons, New York.

4.6 Ejercicios

4.1. En este ejercicio, consideramos la relación entre dos estadísticas que resumen qué tan bien se ajusta un modelo de regresión, la razón \(F\) y \(R^2\), el coeficiente de determinación. (Aquí, la razón \(F\) es la estadística utilizada para probar la adecuación del modelo, no una estadística parcial \(F\)).

1. Escribe \(R^2\) en términos de \(Error ~SS\) y \(Regression ~SS\).
2. Escribe la razón \(F\) en términos de \(Error ~SS\), \(Regression ~SS\), \(k\), y \(n\).
3. Establece la relación algebraica \[ F\text{-ratio} = \frac{R^2}{1-R^2} \frac{n-(k+1)}{k}. \]
4. Supongamos que \(n = 40\), \(k = 5\), y \(R^2 = 0.20\). Calcula la razón \(F\). Realiza la prueba habitual de adecuación del modelo para determinar si las cinco variables explicativas afectan significativamente de manera conjunta a la variable de respuesta.
5. Supongamos que \(n = 400\) (no 40), \(k = 5\), y \(R^2 = 0.20\). Calcula la razón \(F\). Realiza la prueba habitual de adecuación del modelo para determinar si las cinco variables explicativas afectan significativamente de manera conjunta a la variable de respuesta.

4.2. Costos Hospitalarios. Este ejercicio considera los datos de gastos hospitalarios proporcionados por la Agencia de Investigación y Calidad de la Atención Médica de EE. UU. (AHRQ) y descritos en el Ejercicio 1.4.

1. Produce un diagrama de dispersión, una correlación, y una regresión lineal de LNTOTCHG en función de AGE. ¿Es AGE un predictor significativo de LNTOTCHG?
2. Te preocupa que los recién nacidos sigan un patrón diferente al de otras edades. Crea una variable binaria que indique si AGE es igual a cero o no. Ejecuta una regresión utilizando esta variable binaria y AGE como variables explicativas. ¿Es la variable binaria estadísticamente significativa?
3. Ahora examina el efecto del género, usando la variable binaria FEMALE que es uno si el paciente es mujer y cero en caso contrario. Ejecuta una regresión utilizando AGE y FEMALE como variables explicativas. Realiza una segunda regresión que incluya estas dos variables con un término de interacción. Comenta si el efecto del género es importante en alguno de los modelos.
4. Ahora considera el tipo de admisión, APRDRG, un acrónimo de “grupo de diagnóstico refinado para todos los pacientes”. Esta es una variable categórica explicativa que proporciona información sobre el tipo de admisión hospitalaria. Hay varios cientos de niveles de esta categoría. Por ejemplo, el nivel 640 representa la admisión de un recién nacido normal, con un peso neonatal mayor o igual a 2.5 kilogramos. Como otro ejemplo, el nivel 225 representa una admisión que resulta en una apendicectomía.
   d(i). Ejecuta un modelo ANOVA de un factor, utilizando APRDRG para predecir LNTOTCHG. Examina el \(R^2\) de este modelo y compáralo con el coeficiente de determinación del modelo de regresión lineal de LNTOTCHG en función de AGE. Basándote en esta comparación, ¿qué modelo crees que es preferido?
   d(ii). Para el modelo de un factor en la parte d(i), proporciona un intervalo de confianza del 95% para la media de LNTOTCHG para el nivel 225 correspondiente a una apendicectomía. Convierte tu respuesta final de dólares logarítmicos a dólares mediante exponenciación.
   d(iii). Ejecuta un modelo de regresión de APRDRG, FEMALE, y AGE en LNTOTCHG. Indica si AGE es un predictor estadísticamente significativo de LNTOTCHG. Indica si FEMALE es un predictor estadísticamente significativo de LNTOTCHG.

4.3. Utilización de Hogares de Ancianos. Este ejercicio considera los datos de hogares de ancianos proporcionados por el Departamento de Servicios de Salud y Familia de Wisconsin (DHFS) y descritos en los Ejercicios 1.2, 2.10, y 2.20.

Además de las variables de tamaño, también tenemos información sobre varias variables binarias. La variable URBAN se utiliza para indicar la ubicación de la instalación. Es uno si la instalación se encuentra en un entorno urbano y cero en caso contrario. La variable MCERT indica si la instalación está certificada por Medicare. La mayoría, pero no todos, los hogares de ancianos están certificados para proporcionar atención financiada por Medicare. Hay tres estructuras organizativas para los hogares de ancianos: gobierno (estado, condados, municipios), empresas con fines de lucro y organizaciones exentas de impuestos. Periódicamente, las instalaciones pueden cambiar de propietario y, con menos frecuencia, de tipo de propiedad. Creamos dos variables binarias PRO y TAXEXEMPT para denotar empresas con fines de lucro y organizaciones exentas de impuestos, respectivamente. Algunos hogares de ancianos optan por no comprar cobertura de seguro privado para sus empleados. En cambio, estas instalaciones proporcionan directamente seguros y beneficios de pensión a sus empleados; esto se conoce como “auto-financiamiento del seguro”. Usamos la variable binaria SELFFUNDINS para denotarlo.

Decides examinar la relación entre LOGTPY (\(y\)) y las variables explicativas. Usa los datos del año 2001 del informe de costos y realiza el siguiente análisis.

1. Hay tres niveles de estructuras organizativas, pero solo utilizamos dos variables binarias (PRO y TAXEXEMPT). Explica por qué.
2. Realiza un análisis de varianza de un factor usando TAXEXEMPT como el factor. Decide si exento de impuestos es o no un factor importante para determinar LOGTPY. Establece tu hipótesis nula, hipótesis alternativa y todos los componentes de la regla de toma de decisiones. Utiliza un nivel de significancia del 5%.
3. Realiza un análisis de varianza de un factor usando MCERT como el factor. Decide si MCERT es o no un factor importante para determinar LOGTPY.
   c(i). Proporciona una estimación puntual de LOGTPY para una instalación de enfermería que no está certificada por Medicare.
   c(ii). Proporciona un intervalo de confianza del 95% para tu estimación puntual en la parte (i).
   
4. Ejecuta un modelo de regresión usando las variables binarias, URBAN, PRO, TAXEXEMPT, SELFFUNDINS, y MCERT. Encuentra \(R^2\). ¿Qué variables son estadísticamente significativas?
5. Ejecuta un modelo de regresión usando todas las variables explicativas, LOGNUMBED, LOGSQRFOOT, URBAN, PRO, TAXEXEMPT, SELFFUNDINS, y MCERT. Encuentra \(R^2\). ¿Qué variables son estadísticamente significativas?
   e(i). Calcula la correlación parcial entre LOGTPY y LOGSQRFOOT. Compárala con la correlación entre LOGTPY y LOGSQRFOOT. Explica por qué la correlación parcial es pequeña.
   e(ii). Compara el bajo nivel de los \(t\)-ratios (para probar la importancia de los coeficientes de regresión individuales) y el alto nivel de la razón \(F\) (para probar la adecuación del modelo). Describe la aparente inconsistencia y proporciona una explicación para esta inconsistencia.

4.4. Reclamaciones de Seguros de Automóviles. Consulta el Ejercicio 1.3.

1. Ejecuta una regresión de LNPAID en AGE. ¿Es AGE una variable estadísticamente significativa? Para responder a esta pregunta, usa una prueba formal de hipótesis. Establece tu hipótesis nula y alternativa, el criterio de toma de decisiones y tu regla de toma de decisiones. También comenta sobre la bondad del ajuste de esta variable.
2. Considera usar la clase como una sola variable explicativa. Usa el factor único para estimar el modelo y responde a las siguientes preguntas.
   b(i). ¿Cuál es la estimación puntual de las reclamaciones en la clase C7, conductores de 50-69 años, que conducen al trabajo o la escuela, menos de 30 millas por semana con un kilometraje anual inferior a 7500, en unidades logarítmicas naturales?
   b(ii). Determina el intervalo de confianza del 95% correspondiente de las reclamaciones esperadas, en unidades logarítmicas naturales.
   b(iii). Convierte el intervalo de confianza del 95% de las reclamaciones esperadas que determinaste en la parte b(ii) a dólares.
   
3. Ejecuta una regresión de LNPAID en AGE, GENDER, y las variables categóricas STATE CODE y CLASS.
   c(i). ¿Es GENDER una variable estadísticamente significativa? Para responder a esta pregunta, usa una prueba formal de hipótesis. Establece tu hipótesis nula y alternativa, el criterio de toma de decisiones y tu regla de toma de decisiones.
   c(ii). ¿Es CLASS una variable estadísticamente significativa? Para responder a esta pregunta, usa una prueba formal de hipótesis. Establece tu hipótesis nula y alternativa, el criterio de toma de decisiones y tu regla de toma de decisiones.
   c(iii). Usa el modelo para proporcionar una estimación puntual de las reclamaciones en dólares (no en dólares logarítmicos) para un hombre de 60 años en el STATE 2 en la CLASS C7.
   c(iv). Escribe el coeficiente asociado con la CLASS C7 e interpreta este coeficiente.

4.5. Ventas de la Lotería de Wisconsin. Este ejercicio considera los datos de ventas de lotería del Estado de Wisconsin que se describieron en la Sección 2.1 y se examinaron en el Ejercicio 3.4.

Parte 1: Decides examinar la relación entre SALES (\(y\)) y las ocho variables explicativas (PERPERHH, MEDSCHYR, MEDHVL, PRCRENT, PRC55P, HHMEDAGE, MEDINC, y POP).

1. Ajusta un modelo de regresión de SALES en las ocho variables explicativas.

2. Encuentra \(R^2\).
   b(i). Utilízalo para calcular el coeficiente de correlación entre los valores observados y los valores ajustados.
   b(ii). Quieres usar \(R^2\) para probar la adecuación del modelo en la parte (a). Usa una prueba formal de hipótesis. Establece tu hipótesis nula y alternativa, el criterio de toma de decisiones y tus reglas de toma de decisiones.
   

3. Prueba si POP, MEDSCHYR, y MEDHVL son variables explicativas importantes de forma conjunta para comprender SALES.

   Parte 2: Después del análisis preliminar en la Parte 1, decides examinar la relación entre SALES (\(y\)) y POP, MEDSCHYR, y MEDHVL.

4. Ajusta un modelo de regresión de SALES en estas tres variables explicativas.

5. ¿Ha disminuido el coeficiente de determinación del modelo de regresión de ocho variables al modelo de tres variables? ¿Significa esto que el modelo no ha mejorado o proporciona poca información? Explica tu respuesta.

6. Para determinar formalmente si se debe usar el modelo de tres o de ocho variables, utiliza una prueba parcial \(F\). Establece tu hipótesis nula y alternativa, el criterio de toma de decisiones y tus reglas de toma de decisiones.

4.6. Gastos de Compañías de Seguros. Este ejercicio considera los datos de compañías de seguros del NAIC y descritos en los Ejercicios 1.6 y 3.5.

1. ¿Son importantes los términos cuadrados?

Considera un modelo lineal de LNEXPENSES con doce variables explicativas. Para las variables explicativas, incluye ASSETS, GROUP, ambas versiones de pérdidas y primas brutas, así como las dos variables BLS. También incluye el cuadrado de cada una de las dos pérdidas y las dos primas brutas.

Prueba si los cuatro términos cuadrados son conjuntamente estadísticamente significativos, usando una prueba parcial \(F\). Establece tus hipótesis nula y alternativa, el criterio de toma de decisiones y tus reglas de toma de decisiones.

2. ¿Son importantes los términos de interacción con GROUP?

Omite las dos variables BLS, de manera que ahora hay once variables: ASSETS, GROUP, ambas versiones de pérdidas y primas brutas, así como las interacciones de GROUP con ASSETS y ambas versiones de pérdidas y primas brutas.

Prueba si los cinco términos de interacción son conjuntamente estadísticamente significativos, usando una prueba parcial \(F\). Establece tus hipótesis nula y alternativa, el criterio de toma de decisiones y tus reglas de toma de decisiones.

3. Estás examinando una compañía que no está en la muestra con valores LONGLOSS = 0.025, SHORTLOSS = 0.040, GPWPERSONAL = 0.050, GPWCOMM = 0.120, ASSETS = 0.400, CASH = 0.350, y GROUP = 1.

Usa el modelo de interacción de once variables de la parte (b) para producir un intervalo de predicción del 95% para esta compañía.

4.7. Expectativas de Vida Nacionales. Continuamos el análisis iniciado en los Ejercicios 1.7, 2.22, y 3.6.

1. Considera la regresión utilizando tres variables explicativas, FERTILITY, PUBLICEDUCATION, y ln(HEALTH) que hiciste en el Ejercicio 3.6. Prueba si PUBLICEDUCATION y ln(HEALTH) son conjuntamente estadísticamente significativos, usando una prueba parcial \(F\). Establece tus hipótesis nula y alternativa, el criterio de toma de decisiones y tus reglas de toma de decisiones. (Sugerencia: Usa la forma del coeficiente de determinación para calcular el estadístico de la prueba.) Proporciona un valor aproximado de \(p\) para la prueba.

2. Ahora introducimos la variable REGION, resumida en la Tabla 4.11. Un diagrama de caja de las expectativas de vida versus REGION se muestra en la Figura 4.8. Describe lo que aprendemos de la Tabla y el diagrama de caja sobre el efecto de REGION en LIFEEXP.

Figura 4.8: Diagramas de Caja de LIFEEXP por REGION

La Tabla 4.11 resume la esperanza de vida promedio por región.

REGIÓN	Descripción de la Región	Número	Media
1	Estados Árabes	13	71.9
2	Asia Oriental y Pacífico	17	69.1
3	América Latina y el Caribe	25	72.8
4	Asia Meridional	7	65.1
5	Europa Meridional	3	67.4
6	África Subsahariana	38	52.2
7	Europa Central y Oriental	24	71.6
8	OECD de Altos Ingresos	23	79.6
	Todos	150	67.4

3. Ajusta un modelo de regresión utilizando solo el factor REGION. ¿Es REGION un determinante estadísticamente significativo de LIFEEXP? Establece tus hipótesis nula y alternativa, el criterio de toma de decisiones y tus reglas de toma de decisiones.

4. Ajusta un modelo de regresión utilizando tres variables explicativas, FERTILITY, PUBLICEDUCATION, y ln(HEALTH), así como la variable categórica REGION.
   d(i). Estás examinando un país que no está en la muestra con valores FERTILITY = 2.0, PUBLICEDUCATION = 5.0, y ln(HEALTH) = 1.0. Produce dos valores predichos de esperanza de vida asumiendo que el país es de (1) un estado árabe y (2) África Subsahariana.
   d(ii). Proporciona un intervalo de confianza del 95% para la diferencia en expectativas de vida entre un estado árabe y un país de África Subsahariana.
   d(iii). Proporciona la estimación puntual (usualmente de mínimos cuadrados ordinarios) para la diferencia en expectativas de vida entre un país de África Subsahariana y un país de altos ingresos de la OECD (Organización para la Cooperación y el Desarrollo Económico).

4.7 Suplemento Técnico - Expresiones Matriciales

4.7.1 Expresión de Modelos con Variables Categóricas en Forma Matricial

El Capítulo 3 mostró cómo escribir la ecuación del modelo de regresión en la forma \(\mathbf{y = X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}\) donde \(\mathbf{X}\) es una matriz de variables explicativas. Esta forma permite el cálculo directo de los coeficientes de regresión, \(\mathbf{b} = \left(\mathbf{X}^{\prime} \mathbf{X}\right)^{-1} \mathbf{X}^{\prime} \mathbf{y}\). Esta sección muestra cómo el modelo y los cálculos se reducen a expresiones más simples cuando las variables explicativas son categóricas.

Modelo con una Variable Categórica. Considera el modelo con una variable categórica introducido en la Sección 4.3 con \(c\) niveles de la variable categórica. A partir de la ecuación (4.9), este modelo se puede escribir como

\[ \mathbf{y} = \begin{bmatrix} y_{1,1} \\ \cdot \\ \cdot \\ \cdot \\ y_{n_1,1} \\ \cdot \\ \cdot \\ \cdot \\ y_{1,c} \\ \cdot \\ \cdot \\ \cdot \\ y_{n_{c},c} \end{bmatrix} = \begin{bmatrix} 1 & 0 & \cdots & 0 \\ \cdot & \cdot & \cdots & \cdot \\ \cdot & \cdot & \cdots & \cdot \\ \cdot & \cdot & \cdots & \cdot \\ 1 & 0 & \cdots & \cdots \\ \cdot & \cdot & \cdots & \cdot \\ \cdot & \cdot & \cdots & \cdot \\ \cdot & \cdot & \cdots & \cdot \\ 0 & 0 & \cdots & 1 \\ \cdot & \cdot & \cdots & \cdot \\ \cdot & \cdot & \cdots & \cdot \\ \cdot & \cdot & \cdots & \cdot \\ 0 & 0 & \cdots & 1 \\ \end{bmatrix} \begin{bmatrix} \mu_1 \\ \cdot \\ \cdot \\ \cdot \\ \mu_c \end{bmatrix} + \begin{bmatrix} \varepsilon_{1,1} \\ \cdot \\ \cdot \\ \cdot \\ \varepsilon_{n_1,1} \\ \cdot \\ \cdot \\ \cdot \\ \varepsilon_{1,c} \\ \cdot \\ \cdot \\ \cdot \\ \varepsilon_{n_{c},c} \end{bmatrix} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon} \]

Para hacer la notación más compacta, escribimos \(\mathbf{0}\) y \(\mathbf{1}\) para una columna de ceros y unos, respectivamente. Con esta convención, otra forma de expresarlo es

\[ \mathbf{y} = \begin{bmatrix} \mathbf{1}_1 & \mathbf{0}_1 & \cdots & \mathbf{0}_1 \\ \mathbf{0}_2 & \mathbf{1}_2 & \cdots & \mathbf{0}_2 \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{0}_c & \mathbf{0}_c & \cdots & \mathbf{1}_c \end{bmatrix} \begin{bmatrix} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_c \end{bmatrix} + \boldsymbol{\varepsilon} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon} \tag{4.14} \]

Aquí, \(\mathbf{0}_1\) y \(\mathbf{1}_1\) representan columnas de vectores de longitud \(n_1\) de ceros y unos, respectivamente, y de manera similar para \(\mathbf{0}_2, \mathbf{1}_2, \ldots, \mathbf{0}_c, \mathbf{1}_c\).

La ecuación (4.14) nos permite aplicar la maquinaria desarrollada para el modelo de regresión al modelo con una variable categórica. Como cálculo intermedio, tenemos

\[ \begin{array}{ll} (\mathbf{X}^{\prime} \mathbf{X})^{-1} &= \left( \begin{bmatrix} \mathbf{1}_1 & \mathbf{0}_2 & \cdots & \mathbf{0}_c \\ \mathbf{0}_1 & \mathbf{1}_2 & \cdots & \mathbf{0}_c \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{0}_1 & \mathbf{0}_2 & \cdots & \mathbf{1}_c \end{bmatrix}^{\prime} \begin{bmatrix} \mathbf{1}_1 & \mathbf{0}_1 & \cdots & \mathbf{0}_1 \\ \mathbf{0}_2 & \mathbf{1}_2 & \cdots & \mathbf{0}_2 \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{0}_c & \mathbf{0}_c & \cdots & \mathbf{1}_c \end{bmatrix} \right)^{-1}\\ &= \begin{bmatrix} n_1 & 0 & \cdots & 0 \\ 0 & n_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & n_c \end{bmatrix}^{-1} = \begin{bmatrix} \frac{1}{n_1} & 0 & \cdots & 0 \\ 0 & \frac{1}{n_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \frac{1}{n_c} \end{bmatrix} . \tag{4.15} \end{array} \]

Así, las estimaciones de los parámetros son

\[ \mathbf{b} = \begin{bmatrix} \hat{\mu}_1 \\ \vdots \\ \hat{\mu}_c \end{bmatrix} = (\mathbf{X}^{\prime} \mathbf{X})^{-1} \mathbf{X}^{\prime} \mathbf{y} = \begin{bmatrix} \frac{1}{n_1} & 0 & \cdots & 0 \\ 0 & \frac{1}{n_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \frac{1}{n_c} \end{bmatrix} \begin{bmatrix} \mathbf{1}_1 & \mathbf{0}_2 & \cdots & \mathbf{0}_c \\ \mathbf{0}_1 & \mathbf{1}_2 & \cdots & \mathbf{0}_c \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{0}_1 & \mathbf{0}_2 & \cdots & \mathbf{1}_c \end{bmatrix}^{\prime} \begin{bmatrix} y_{1,1} \\ \vdots \\ y_{n_1,1} \\ \vdots \\ y_{1,c} \\ \vdots \\ y_{n_{c},c} \end{bmatrix} \]

\[ = \begin{bmatrix} \frac{1}{n_1} & 0 & \cdots & 0 \\ 0 & \frac{1}{n_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \frac{1}{n_c} \end{bmatrix} \begin{bmatrix} \sum_{i=1}^{n_1} y_{i1} \\ \vdots \\ \sum_{i=1}^{n_c} y_{ic} \end{bmatrix} = \begin{bmatrix} \bar{y}_1 \\ \vdots \\ \bar{y}_c \end{bmatrix} \tag{4.16} \]

Hemos visto que la estimación por mínimos cuadrados de \(\mu_j\), \(\bar{y}_j\), se puede obtener directamente de la ecuación (4.9). Al reescribir el modelo en notación de regresión matricial, podemos recurrir a los resultados del modelo de regresión y no necesitamos probar las propiedades de los modelos con variables categóricas desde los principios básicos. Es decir, dado que este modelo está en formato de regresión, tenemos inmediatamente todas las propiedades del modelo de regresión.

Indicar a tu software que una variable es categórica puede significar cálculos más eficientes, como en los cálculos de las estimaciones de regresión por mínimos cuadrados en la ecuación (4.16). Además, el cálculo de otras cantidades también se puede hacer de manera más directa. Como otro ejemplo, tenemos que el error estándar de \(\hat{\mu}_j\) es

\[ se(\hat{\mu}_j) = s ~ \sqrt{j \text{ th } \textit{ diagonal element of } \mathbf{(X}^{\prime}\mathbf{X)}^{-1}} = s/\sqrt{n_j}. \]

Modelo con Una Variable Categórica y Una Continua

Como otra ilustración, consideramos el modelo de intercepto variable y pendiente constante. Este modelo se resume como \(\mathbf{y} = \mathbf{X} \boldsymbol \beta + \boldsymbol \varepsilon\) donde

\[ \mathbf{X} = \begin{bmatrix} \mathbf{1}_1 & \mathbf{0}_1 & \cdots & \mathbf{0}_1 & \mathbf{x}_1 \\ \mathbf{0}_2 & \mathbf{1}_2 & \cdots & \mathbf{0}_2 & \mathbf{x}_2 \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \mathbf{0}_{c} & \mathbf{0}_{c} & \cdots & \mathbf{1}_c & \mathbf{x}_{c} \end{bmatrix} \text{ y } \boldsymbol \beta = \begin{bmatrix} \beta_{01} \\ \beta_{02} \\ \cdots \\ \cdots \\ \cdots \\ \beta_{0c} \\ \beta_1 \end{bmatrix}. \tag{4.17} \]

Aquí, \(\mathbf{0}_j\) y \(\mathbf{1}_j\) representan columnas de vectores de longitud \(n_j\) de ceros y unos, respectivamente, y \(\mathbf{x}_j = (x_{1j}, x_{2j}, \ldots, x_{n_j, j})^{\prime}\) es la columna de la variable continua en el nivel \(j\). Técnicas de álgebra matricial sencillas proporcionan las estimaciones por mínimos cuadrados.

4.7.2 Cálculo Recursivo de Mínimos Cuadrados

Cuando se calculan los coeficientes de regresión utilizando mínimos cuadrados, \(\mathbf{b} = \left(\mathbf{X}^{\prime} \mathbf{X}\right)^{-1} \mathbf{X}^{\prime} \mathbf{y}\), para algunas aplicaciones, la dimensión de \(\mathbf{X}^{\prime} \mathbf{X}\) puede ser grande, lo que causa dificultades computacionales. Afortunadamente, para algunos problemas, los cálculos se pueden dividir en problemas más pequeños que se pueden resolver de forma recursiva.

Cálculo Recursivo de Mínimos Cuadrados. Supongamos que la función de regresión se puede escribir como

\[ \mathrm{E}~\mathbf{y} = \mathbf{X} \boldsymbol \beta = \left( \mathbf{X}_1 : \mathbf{X}_2 \right) \left( \begin{array}{c} \boldsymbol \beta_1 \\ \boldsymbol \beta_2 \\ \end{array} \right), \tag{4.18} \]

donde \(\mathbf{X}_1\) tiene dimensiones \(n \times k_1\), \(\mathbf{X}_2\) tiene dimensiones \(n \times k_2\), \(k_1 + k_2 = k\), \(\boldsymbol \beta_1\) tiene dimensiones \(k_1 \times 1\), y \(\boldsymbol \beta_2\) tiene dimensiones \(k_2 \times 1\). Definimos \(\mathbf{Q}_1 = \mathbf{I} - \mathbf{X}_1 \left(\mathbf{X}_1^{\prime} \mathbf{X}_1\right)^{-1} \mathbf{X}_1^{\prime}\). Entonces, el estimador por mínimos cuadrados se puede calcular como:

\[ \mathbf{b} = \left( \begin{array}{c} \mathbf{b}_1 \\ \mathbf{b}_2 \\ \end{array} \right) = \left( \begin{array}{c} (\mathbf{X}_1^{\prime} \mathbf{X}_1)^{-1} \mathbf{X}_1^{\prime} \left( \mathbf{y} - \mathbf{X}_2 \mathbf{b}_2 \right) \\ \left(\mathbf{X}_2^{\prime} \mathbf{Q}_1 \mathbf{X}_2\right)^{-1} \mathbf{X}_2^{\prime} \mathbf{Q}_1 \mathbf{y} \\ \end{array} \right). \tag{4.19} \]

La ecuación (4.19) proporciona el primer paso en la recursión. Puede ser iterada fácilmente para permitir una descomposición más detallada de \(\mathbf{X}\).

Caso Especial: Modelo con Una Variable Categórica y Una Continua. Para ilustrar la relevancia de la ecuación (4.19), consideremos el modelo resumido en la ecuación (4.17). Aquí, la dimensión de \(\mathbf{X}\) es \(n \times (c+1)\) y, por lo tanto, la dimensión de \(\mathbf{X}^{\prime} \mathbf{X}\) es \((c+1) \times (c+1)\). Tomar la inversa de esta matriz podría ser difícil si \(c\) es grande. Para aplicar la ecuación (4.19), definimos

\[ \mathbf{X}_1 = \begin{bmatrix} \mathbf{1}_1 & \mathbf{0}_1 & \cdots & \mathbf{0}_1 \\ \mathbf{0}_2 & \mathbf{1}_2 & \cdots & \mathbf{0}_2 \\ \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots \\ \mathbf{0}_c & \mathbf{0}_c & \cdots & \mathbf{1}_c \end{bmatrix} \text{ y } \mathbf{X}_2 = \begin{bmatrix} \mathbf{x}_1 \\ \mathbf{x}_2 \\ \cdots \\ \cdots \\ \cdots \\ \mathbf{x}_c \end{bmatrix}. \]

En este caso, hemos visto en la ecuación (4.15) cómo es sencillo calcular \(\left(\mathbf{X}_1^{\prime} \mathbf{X}_1\right)^{-1}\) sin necesidad de invertir matrices. Esto hace que el cálculo de \(\mathbf{Q}_1\) sea directo. Con esto, podemos calcular \(\mathbf{X}_2^{\prime} \mathbf{Q}_1 \mathbf{X}_2\) y, dado que es un escalar, obtener inmediatamente su inversa. Esto proporciona \(\mathbf{b}_2\), que luego se usa para calcular \(\mathbf{b}_1\). Aunque este procedimiento no es tan directo como \(\mathbf{b} = \left(\mathbf{X}^{\prime} \mathbf{X}\right)^{-1} \mathbf{X}^{\prime} \mathbf{y}\), puede ser computacionalmente eficiente.

Resultados de Matrices Particionadas

Para establecer la ecuación (4.19), utilizamos resultados estándar en álgebra matricial respecto a las inversas de matrices particionadas.

Resultados de Matrices Particionadas. Supongamos que podemos particionar la matriz \((p+q) \times (p+q)\) \(\mathbf{B}\) como

\[ \mathbf{B} = \begin{bmatrix} \mathbf{B}_{11} & \mathbf{B}_{12} \\ \mathbf{B}_{12}^{\prime} & \mathbf{B}_{22} \end{bmatrix}, \]

donde \(\mathbf{B}_{11}\) es una matriz \(p \times p\) invertible, \(\mathbf{B}_{22}\) es una matriz \(q \times q\) invertible, y \(\mathbf{B}_{12}\) es una matriz \(p \times q\). Entonces

\[ \mathbf{B}^{-1} = \begin{bmatrix} \mathbf{C}_{11}^{-1} & - \mathbf{B}_{11}^{-1} \mathbf{B}_{12} \mathbf{C}_{22}^{-1} \\ - \mathbf{C}_{22}^{-1} \mathbf{B}_{12}^{\prime} \mathbf{B}_{11}^{-1} & \mathbf{C}_{22}^{-1} \end{bmatrix}, \tag{4.20} \]

donde \(\mathbf{C}_{11} = \mathbf{B}_{11} - \mathbf{B}_{12} \mathbf{B}_{22}^{-1} \mathbf{B}_{12}^{\prime}\) y \(\mathbf{C}_{22} = \mathbf{B}_{22} - \mathbf{B}_{12}^{\prime} \mathbf{B}_{11}^{-1} \mathbf{B}_{12}.\)

Para verificar la ecuación (4.20), multiplique \(\mathbf{B}^{-1}\) por \(\mathbf{B}\) para obtener la matriz identidad \(\mathbf{I}\). Además,

\[ \mathbf{C}_{11}^{-1} = \mathbf{B}_{11}^{-1} + \mathbf{B}_{11}^{-1} \mathbf{B}_{12} \mathbf{C}_{22}^{-1} \mathbf{B}_{12}^{\prime} \mathbf{B}_{11}^{-1}. \tag{4.21} \]

Ahora, primero escribimos el estimador de mínimos cuadrados como \[ \begin{array}{ll} \mathbf{b} &= \left( \mathbf{X}^{\prime}\mathbf{X}\right)^{-1} \mathbf{X}^{\prime} \mathbf{y} = \left( \left( \begin{array}{c} \mathbf{X}_1^{\prime} \\ \mathbf{X}_2^{\prime} \\ \end{array} \right) \left( \mathbf{X}_1 : \mathbf{X}_2 \right)\right)^{-1} \left( \begin{array}{c} \mathbf{X}_1^{\prime} \\ \mathbf{X}_2^{\prime} \\ \end{array} \right) \mathbf{y} \\ & = \left( \begin{array}{cc} \mathbf{X}_1^{\prime} \mathbf{X}_1 & \mathbf{X}_1^{\prime} \mathbf{X}_2 \\ \mathbf{X}_2^{\prime} \mathbf{X}_1 & \mathbf{X}_2^{\prime} \mathbf{X}_2 \\ \end{array} \right)^{-1} \left( \begin{array}{c} \mathbf{X}_1^{\prime} \mathbf{y} \\ \mathbf{X}_2^{\prime} \mathbf{y} \\ \end{array} \right) = \left( \begin{array}{c} \mathbf{b}_1 \\ \mathbf{b}_2 \\ \end{array} \right). \end{array} \]

Para aplicar los resultados de matrices particionadas, definimos \[ \mathbf{Q}_j = \mathbf{I} - \mathbf{X}_j \left(\mathbf{X}_j^{\prime}\mathbf{X}_j \right)^{-1} \mathbf{X}_j^{\prime}, \] donde \(j=1,2\), y \(\mathbf{B}_{j,k} = \mathbf{X}_j^{\prime}\mathbf{X}_k\) para \(j,k=1,2.\) Esto significa que \(\mathbf{C}_{11}=\mathbf{X}_1^{\prime}\mathbf{X}_1 - \mathbf{X}_1^{\prime}\mathbf{X}_2 (\mathbf{X}_2^{\prime}\mathbf{X}_2)^{-1} \mathbf{X}_2^{\prime}\mathbf{X}_1^{\prime }\) \(= \mathbf{X}_1^{\prime} \mathbf{Q}_2 \mathbf{X}_1\) y de manera similar \(\mathbf{C}_{22} = \mathbf{X}_2^{\prime} \mathbf{Q}_1 \mathbf{X}_2\). A partir de la segunda fila, tenemos \[ \begin{array}{ll} \mathbf{b}_2 &= \mathbf{C}_{22}^{-1} \left( -\mathbf{B}_{12}^{\prime} \mathbf{B}_{11}^{-1}\mathbf{X}_1^{\prime} \mathbf{y} + \mathbf{X}_2^{\prime} \mathbf{y} \right) \\ &= \left(\mathbf{X}_2^{\prime} \mathbf{Q}_1 \mathbf{X}_2 \right)^{-1} \left( - \mathbf{X}_2^{\prime} \mathbf{X}_1 (\mathbf{X}_1^{\prime}\mathbf{X}_1)^{-1} \mathbf{X}_1^{\prime} \mathbf{y} + \mathbf{X}_2^{\prime}\mathbf{y} \right) \\ &= \left(\mathbf{X}_2^{\prime} \mathbf{Q}_1 \mathbf{X}_2 \right)^{-1} \mathbf{X}_2^{\prime} \mathbf{Q}_1\mathbf{y}. \end{array} \]

A partir de la primera fila,

\[ \begin{array}{ll} \mathbf{b}_1 &= \mathbf{C}_{11}^{-1} \mathbf{X}_1^{\prime}\mathbf{y} - \mathbf{B}_{11}^{-1}\mathbf{B}_{12}\mathbf{C}_{22}^{-1} \mathbf{X}_2^{\prime}\mathbf{y} \\ &= \left( \mathbf{B}_{11}^{-1} + \mathbf{B}_{11}^{-1} \mathbf{B}_{12} \mathbf{C}_{22}^{-1} \mathbf{B}_{21} \mathbf{B}_{11}^{-1} \right) \mathbf{X}_1^{\prime}\mathbf{y} - \mathbf{B}_{11}^{-1}\mathbf{B}_{12}\mathbf{C}_{22}^{-1} \mathbf{X}_2^{\prime}\mathbf{y} \\ &= \mathbf{B}_{11}^{-1}\mathbf{X}_1^{\prime}\mathbf{y} - \mathbf{B}_{11}^{-1} \mathbf{B}_{12} \mathbf{C}_{22}^{-1} \left( -\mathbf{B}_{21} \mathbf{B}_{11}^{-1} \mathbf{X}_1^{\prime}\mathbf{y} + \mathbf{X}_2^{\prime}\mathbf{y} \right)\\ &= \mathbf{B}_{11}^{-1}\mathbf{X}_1^{\prime}\mathbf{y} - \mathbf{B}_{11}^{-1} \mathbf{B}_{12} \mathbf{b}_2 \\ &= (\mathbf{X}_1^{\prime}\mathbf{X}_1)^{-1}\mathbf{X}_1^{\prime}\mathbf{y} - (\mathbf{X}_1^{\prime}\mathbf{X}_1)^{-1} \mathbf{X}_1^{\prime}\mathbf{X}_2 \mathbf{b}_2 \\ &= (\mathbf{X}_1^{\prime}\mathbf{X}_1)^{-1}\mathbf{X}_1^{\prime} \left( \mathbf{y} - \mathbf{X}_2 \mathbf{b}_2 \right). \end{array} \]

Esto establece la ecuación (4.19).

Modelo Reparametrizado. Para la función de regresión particionada en la ecuación (4.18), definimos \(\mathbf{A}= \left( \mathbf{X}_1^{\prime} \mathbf{X}_1 \right)^{-1} \mathbf{X}_1^{\prime} \mathbf{X}_2\) y \(\mathbf{E}_2 = \mathbf{X}_2 - \mathbf{X}_1 \mathbf{A}\). Si se realizara una regresión “multivariada” usando \(\mathbf{X}_2\) como la respuesta y \(\mathbf{X}_1\) como variables explicativas, entonces las estimaciones de parámetros serían \(\mathbf{A}\) y los residuos \(\mathbf{E}_2\).

Con estas definiciones, use la ecuación (4.18) para definir el modelo de regresión reparametrizado \[ \begin{array}{ll} \mathbf{y} & = \mathbf{X}_1 \boldsymbol \beta_1 + \mathbf{X}_2 \boldsymbol \beta_2 + \boldsymbol \varepsilon = \mathbf{X}_1 \boldsymbol \beta_1 + (\mathbf{E}_2 + \mathbf{X}_1 \mathbf{A})\boldsymbol \beta_2 + \boldsymbol \varepsilon \\ & = \mathbf{X}_1 \boldsymbol \alpha_1 + \mathbf{E}_2 \boldsymbol \beta_2 + \boldsymbol \varepsilon, \end{array} \tag{4.22} \] donde \(\boldsymbol \alpha_1 = \boldsymbol \beta_1 + \mathbf{A}\boldsymbol \beta_2\) es un nuevo vector de parámetros. La razón para introducir esta nueva parametrización es que ahora el vector de variables explicativas es ortogonal a las otras variables explicativas, es decir, el álgebra directa muestra que \(\mathbf{X}_1^{\prime }\mathbf{E}_2=\mathbf{0}\).

Según la ecuación (4.19), el vector de estimaciones de mínimos cuadrados es \[ \begin{array}{ll} \mathbf{a} = \begin{bmatrix} \mathbf{a}_1 \\ \mathbf{b}_2 \end{bmatrix} = \left( \begin{bmatrix} \mathbf{X}_1^{\prime} \\ \mathbf{E}_2^{\prime} \end{bmatrix} \begin{bmatrix} \mathbf{X}_1 & \mathbf{E}_2 \end{bmatrix} \right) ^{-1} \begin{bmatrix} \mathbf{X}_1^{\prime} \\ \mathbf{E}_2^{\prime} \end{bmatrix} \mathbf{y} = \begin{bmatrix} \left( \mathbf{X}_1^{\prime} \mathbf{X}_1 \right)^{-1} \mathbf{X}_1^{\prime} \mathbf{y} \\ \left( \mathbf{E}_2^{\prime}\mathbf{E}_2\right) ^{-1} \mathbf{E}_2^{\prime}\mathbf{y} \end{bmatrix}. \end{array} \tag{4.23} \]

Suma Extra de Cuadrados. Supongamos que queremos considerar el aumento en la suma de cuadrados del error al pasar de un modelo reducido \[ \mathbf{y} = \mathbf{X}_1 \boldsymbol \beta_1 + \boldsymbol \varepsilon \] a un modelo completo \[ \mathbf{y} = \mathbf{X}_1 \boldsymbol \beta_1 + \mathbf{X}_2 \boldsymbol \beta_2 + \boldsymbol \varepsilon. \] Para el modelo reducido, la suma de cuadrados del error es \[ (Error ~ SS)_{reduced} = \mathbf{y}^{\prime} \mathbf{y} - \mathbf{y}^{\prime} \mathbf{X}_1 (\mathbf{X}_1^{\prime} \mathbf{X}_1)^{-1} \mathbf{X}_1^{\prime} \mathbf{y}. \tag{4.24} \] Usando la versión reparametrizada del modelo completo, la suma de cuadrados del error es \[ \begin{array}{ll} (Error ~ SS)_{full} &= \mathbf{y}^{\prime} \mathbf{y} - \mathbf{a}^{\prime} \begin{bmatrix} \mathbf{X}_1^{\prime} \\ \mathbf{E}_2^{\prime} \end{bmatrix} \mathbf{y} = \mathbf{y}^{\prime}\mathbf{y} - \begin{bmatrix} \left( \mathbf{X}_1^{\prime} \mathbf{X}_1 \right)^{-1} \mathbf{X}_1^{\prime} \mathbf{y} \\ \left( \mathbf{E}_2^{\prime}\mathbf{E}_2\right)^{-1} \mathbf{E}_2^{\prime} \mathbf{y} \end{bmatrix}^{\prime} \begin{bmatrix} \mathbf{X}_1^{\prime} \mathbf{y} \\ \mathbf{E}_2^{\prime}\mathbf{y} \end{bmatrix} \\ &= \mathbf{y}^{\prime} \mathbf{y} - \mathbf{y}^{\prime} \mathbf{X}_1 (\mathbf{X}_1^{\prime} \mathbf{X}_1)^{-1} \mathbf{X}_1^{\prime} \mathbf{y} - \mathbf{y}^{\prime} \mathbf{E}_2 (\mathbf{E}_2^{\prime} \mathbf{E}_2)^{-1} \mathbf{E}_2^{\prime} \mathbf{y}. \tag{4.25} \end{array} \]

Así, la reducción en la suma de cuadrados del error al agregar \(\mathbf{X}_2\) al modelo es \[ (Error ~SS)_{reduced} - (Error ~SS)_{full} = \mathbf{y}^{\prime} \mathbf{E}_2 (\mathbf{E}_2^{\prime} \mathbf{E}_2)^{-1} \mathbf{E}_2^{\prime} \mathbf{y}. \tag{4.26} \] Como se mencionó en la Sección 4.3, la cantidad \((Error ~SS)_{reduced} - (Error ~SS)_{full}\) se llama suma extra de cuadrados, o suma de cuadrados Tipo III. Esto se produce automáticamente por algunos paquetes de software estadístico, evitando así la necesidad de ejecutar regresiones separadas.

4.7.3 Modelo Lineal General

Recuerda el modelo lineal general de la Sección 4.4. Es decir, usamos \[ y_i = \beta_0 x_{i0} + \beta_1 x_{i1} + \ldots + \beta_k x_{ik} + \varepsilon_i, \] o, en notación de matrices, \(\mathbf{y} = \mathbf{X} \boldsymbol \beta + \boldsymbol \varepsilon\). Como antes, utilizamos las Suposiciones F1-F4 (o E1-E4) para que los términos de perturbación sean i.i.d. con media cero y varianza común \(\sigma^2\), y las variables explicativas \(\{x_{i0},x_{i1},x_{i2},\ldots,x_{ik}\}\) sean no estocásticas.

En el modelo lineal general, no requerimos que \(\mathbf{X}^{\prime}\mathbf{X}\) sea invertible. Como hemos visto en el Capítulo 4, una razón importante para esta generalización se relaciona con el manejo de variables categóricas. Es decir, para usar variables categóricas, generalmente se recodifican utilizando variables binarias. Para esta recodificación, generalmente se deben hacer algunos tipos de restricciones en el conjunto de parámetros asociados con las variables indicadoras. Sin embargo, no siempre está claro qué tipo de restricciones son las más intuitivas. Al expresar el modelo sin requerir que \(\mathbf{X}^{\prime}\mathbf{X}\) sea invertible, las restricciones pueden imponerse después de que se realice la estimación, no antes.

Ecuaciones Normales. Incluso cuando \(\mathbf{X}^{\prime}\mathbf{X}\) no es invertible, las soluciones a las ecuaciones normales aún proporcionan estimaciones de mínimos cuadrados de \(\boldsymbol \beta\). Es decir, la suma de cuadrados es \[ SS(\mathbf{b}^{\ast}) = \mathbf{(y - Xb}^{\ast}\mathbf{)}^{\prime}\mathbf{(y - Xb}^{\ast}\mathbf{)}, \] donde \(\mathbf{b}^{\ast} = (b_0^{\ast}, b_1^{\ast}, \ldots, b_k^{\ast})^{\prime}\) es un vector de estimaciones candidatas. Las soluciones de las ecuaciones normales son aquellos vectores \(\mathbf{b}^{\circ }\) que satisfacen las ecuaciones normales \[ \mathbf{X}^{\prime}\mathbf{Xb}^{\circ } = \mathbf{X}^{\prime}\mathbf{y}. \tag{4.27} \]

Usamos la notación \(^{\circ }\) para recordarnos que \(\mathbf{b}^{\circ }\) no tiene que ser único. Sin embargo, es un minimizador de la suma de cuadrados. Para ver esto, considera otro vector candidato \(\mathbf{b}^{\ast}\) y nota que \[ SS(\mathbf{b}^{\ast}) = \mathbf{y}^{\prime}\mathbf{y} - 2\mathbf{b}^{\ast \prime }\mathbf{X}^{\prime}\mathbf{y} + \mathbf{b}^{\ast \prime }\mathbf{X}^{\prime}\mathbf{Xb}^{\ast}. \]

Luego, usando la ecuación (4.27), tenemos \[ SS(\mathbf{b}^{\ast}) - SS(\mathbf{b}^{\circ }) = -2\mathbf{b}^{\ast \prime }\mathbf{X}^{\prime}\mathbf{y} + \mathbf{b}^{\ast \prime }\mathbf{X}^{\prime}\mathbf{Xb}^{\ast} - (-2\mathbf{b}^{\circ \prime }\mathbf{Xy} + \mathbf{b}^{\circ \prime }\mathbf{X}^{\prime}\mathbf{Xb}^{\circ }) \] \[ = -2\mathbf{b}^{\ast \prime }\mathbf{Xb}^{\circ } + \mathbf{b}^{\ast \prime }\mathbf{X}^{\prime}\mathbf{Xb}^{\ast} + \mathbf{b}^{\circ \prime }\mathbf{X}^{\prime}\mathbf{Xb}^{\circ } \] \[ = \mathbf{(b}^{\ast} - \mathbf{b}^{\circ})^{\prime} \mathbf{X}^{\prime} \mathbf{X} (\mathbf{b}^{\ast} - \mathbf{b}^{\circ}) = \mathbf{z}^{\prime} \mathbf{z} \geq 0, \] donde \(\mathbf{z} = \mathbf{X} (\mathbf{b}^{\ast} - \mathbf{b}^{\circ})\). Así, cualquier otro candidato \(\mathbf{b}^{\ast}\) produce una suma de cuadrados al menos tan grande como \(SS(\mathbf{b}^{\circ})\).

Valores Ajustados Únicos

A pesar de que puede haber (infinitas) soluciones a las ecuaciones normales, los valores ajustados resultantes, \(\mathbf{\hat{y}} = \mathbf{Xb}^{\circ}\), son únicos. Para ver esto, supongamos que \(\mathbf{b}_1^{\circ}\) y \(\mathbf{b}_2^{\circ}\) son dos soluciones diferentes de la ecuación (4.27). Sea \(\mathbf{\hat{y}}_1 = \mathbf{Xb}_1^{\circ}\) y \(\mathbf{\hat{y}}_2 = \mathbf{Xb}_2^{\circ}\) los vectores de valores ajustados generados por estas estimaciones. Entonces, \[ \mathbf{(\hat{y}}_1 - \mathbf{\hat{y}}_2)^{\prime} (\mathbf{\hat{y}}_1 - \mathbf{\hat{y}}_2) = \mathbf{(b}_1^{\circ} - \mathbf{b}_2^{\circ})^{\prime} \mathbf{X}^{\prime} \mathbf{X} (\mathbf{b}_1^{\circ} - \mathbf{b}_2^{\circ}) = 0 \] porque \(\mathbf{X}^{\prime} \mathbf{X} (\mathbf{b}_1^{\circ} - \mathbf{b}_2^{\circ}) = \mathbf{X}^{\prime} \mathbf{y} - \mathbf{X}^{\prime} \mathbf{y} = \mathbf{0}\), de la ecuación (4.27). Por lo tanto, tenemos que \(\mathbf{\hat{y}}_1 = \mathbf{\hat{y}}_2\) para cualquier elección de \(\mathbf{b}_1^{\circ}\) y \(\mathbf{b}_2^{\circ}\), estableciendo así la unicidad de los valores ajustados.

Debido a que los valores ajustados son únicos, los residuos también son únicos. Por lo tanto, la suma de cuadrados de los errores y las estimaciones de la variabilidad (como \(s^2\)) también son únicas.

Inversas Generalizadas

Una inversa generalizada de una matriz \(\mathbf{A}\) es una matriz \(\mathbf{B}\) tal que \(\mathbf{ABA = A}\). Usamos la notación \(\mathbf{A}^{\mathbf{-}}\) para denotar la inversa generalizada de \(\mathbf{A}\). En el caso de que \(\mathbf{A}\) sea invertible, entonces \(\mathbf{A}^{\mathbf{-}}\) es única e igual a \(\mathbf{A}^{\mathbf{-1}}\). Aunque existen varias definiciones de inversas generalizadas, la definición anterior es suficiente para nuestros propósitos. Ver Searle (1987) para una discusión más profunda sobre definiciones alternativas de inversas generalizadas.

Con esta definición, se puede mostrar que una solución a la ecuación \(\mathbf{Ab = c}\) puede expresarse como \(\mathbf{b = A}^{-} \mathbf{c}\). Así, podemos expresar una estimación de mínimos cuadrados de \(\boldsymbol \beta\) como \(\mathbf{b}^{\circ} = (\mathbf{X}^{\prime} \mathbf{X})^{-} \mathbf{X}^{\prime} \mathbf{y}\). Los paquetes de software estadístico pueden calcular versiones de \((\mathbf{X}^{\prime} \mathbf{X})^{-}\) y así generar \(\mathbf{b}^{\circ}\).

Funciones Estimables

Anteriormente, vimos que cada valor ajustado \(\hat{y}_i\) es único. Dado que los valores ajustados son simplemente combinaciones lineales de estimaciones de parámetros, parece razonable preguntar qué otras combinaciones lineales de estimaciones de parámetros son únicas. Con este fin, decimos que \(\mathbf{C \boldsymbol \beta}\) es una función estimable de los parámetros si \(\mathbf{Cb}^{\circ}\) no depende (es invariante) de la elección de \(\mathbf{b}^{\circ}\). Debido a que los valores ajustados son invariantes a la elección de \(\mathbf{b}^{\circ}\), tenemos que \(\mathbf{C = X}\) produce un tipo de función estimable. Curiosamente, resulta que todas las funciones estimables son de la forma \(\mathbf{LXb}^{\circ}\), es decir, \(\mathbf{C} = \mathbf{LX}\). Ver Searle (1987, página 284) para una demostración de esto. Así, todas las funciones estimables son combinaciones lineales de valores ajustados, es decir, \(\mathbf{LXb}^{\circ} = \mathbf{L\hat{y}}\).

Las funciones estimables son insesgadas y tienen una varianza que no depende de la elección de la inversa generalizada. Es decir, se puede mostrar que \(\text{E } \mathbf{Cb}^{\circ} = \mathbf{C \boldsymbol \beta}\) y \(\text{Var } \mathbf{Cb}^{\circ} = \sigma^2 \mathbf{C(X}^{\prime} \mathbf{X})^{-} \mathbf{C}^{\prime}\) no depende de la elección de \(\mathbf{(X}^{\prime} \mathbf{X})^{-}\).

Hipótesis Comprobables

Como se describe en la Sección 4.2, a menudo interesa probar \(H_0\): \(\mathbf{C \boldsymbol \beta} = \mathbf{d}\), donde \(\mathbf{d}\) es un vector especificado. Esta hipótesis se dice que es comprobable si \(\mathbf{C \boldsymbol \beta}\) es una función estimable, \(\mathbf{C}\) es de rango completo en filas, y el rango de \(\mathbf{C}\) es menor que el rango de \(\mathbf{X}\). Para ser consistentes con la notación de la Sección 4.2, sea \(p\) el rango de \(\mathbf{C}\) y \(k + 1\) el rango de \(\mathbf{X}\). Recordemos que el rango de una matriz es el menor entre el número de filas linealmente independientes y el número de columnas linealmente independientes. Cuando decimos que \(\mathbf{C}\) tiene rango completo en filas, nos referimos a que hay \(p\) filas en \(\mathbf{C}\), de modo que el número de filas es igual al rango.

Hipótesis Lineal General

Como en la Sección 4.2, la estadística de prueba para examinar \(H_0\): \(\mathbf{C \boldsymbol \beta} = \mathbf{d}\) es \[ F\text{-ratio} = \frac{\mathbf{(Cb}^{\circ} - \mathbf{d})^{\prime} \mathbf{(C(X}^{\prime} \mathbf{X})^{-} \mathbf{C}^{\prime})^{-1} \mathbf{(Cb}^{\circ} - \mathbf{d})}{ps_{full}^2}. \] Note que la estadística \(F\)-ratio no depende de la elección de \(\mathbf{b}^{\circ}\) porque \(\mathbf{C b}^{\circ}\) es invariante a \(\mathbf{b}^{\circ}\). Si \(H_0\): \(\mathbf{C \boldsymbol \beta} = \mathbf{d}\) es una hipótesis comprobable y los errores \(\varepsilon_i\) son i.i.d. \(\text{N}(0, \sigma^2)\), entonces el \(F\)-ratio tiene una distribución \(F\) con \(df_1 = p\) y \(df_2 = n - (k + 1)\).

Modelo de Una Variable Categórica

Ahora ilustramos el modelo lineal general considerando una versión sobre-parametr

izada del modelo de un factor que aparece en la ecuación (4.10) usando \[ y_{ij} = \mu + \tau_j + e_{ij} = \mu + \tau_1 x_{i1} + \tau_2 x_{i2} + \ldots + \tau_c x_{ic} + \varepsilon_{ij}. \] En este punto, no imponemos restricciones adicionales en los parámetros. Como en la ecuación (4.13), esto se puede escribir en forma matricial como \[ \mathbf{y} = \begin{bmatrix} \mathbf{1}_1 & \mathbf{1}_1 & \mathbf{0}_1 & \cdots & \mathbf{0}_1 \\ \mathbf{1}_2 & \mathbf{0}_2 & \mathbf{1}_{\mathbf{2}} & \cdots & \mathbf{0}_2 \\ \cdot & \cdot & \cdot & \cdots & \cdot \\ \mathbf{1}_c & \mathbf{0}_c & \mathbf{0}_c & \cdots & \mathbf{1}_c \end{bmatrix} \begin{bmatrix} \mu \\ \tau_1 \\ \cdot \\ \cdot \\ \cdot \\ \tau_c \end{bmatrix} + \boldsymbol \varepsilon = \mathbf{X \boldsymbol \beta + \boldsymbol \varepsilon}. \]

Así, la matriz \(\mathbf{X}^{\prime} \mathbf{X}\) es \[ \mathbf{X}^{\prime} \mathbf{X} = \begin{bmatrix} n & n_1 & n_2 & \cdots & n_c \\ n_1 & n_1 & 0 & \cdots & 0 \\ n_2 & 0 & n_2 & \cdots & 0 \\ \cdot & \cdot & \cdot & \cdots & \cdot \\ \cdot & \cdot & \cdot & \cdots & \cdot \\ \cdot & \cdot & \cdot & \cdots & \cdot \\ n_c & 0 & 0 & \cdots & n_c \end{bmatrix}. \]

donde \(n = n_1 + n_2 + \ldots + n_{c}\). Esta matriz no es invertible. Para ver esto, note que al sumar las últimas \(c\) filas juntas se obtiene la primera fila. Por lo tanto, las últimas \(c\) filas son una combinación lineal exacta de la primera fila, lo que significa que la matriz no tiene rango completo.

Las estimaciones (no únicas) de mínimos cuadrados se pueden expresar como \[ \mathbf{b}^{\circ} = \begin{bmatrix} \mu^{\circ} \\ \tau_1^{\circ} \\ \cdot \\ \cdot \\ \cdot \\ \tau_c^{\circ} \end{bmatrix} = (\mathbf{X}^{\prime} \mathbf{X})^{-} \mathbf{X}^{\prime} \mathbf{y}. \] Las funciones estimables son combinaciones lineales de los valores ajustados. Dado que los valores ajustados son \(\hat{y}_{ij} = \bar{y}_j\), las funciones estimables pueden expresarse como \(L = \sum_{j=1}^{c} a_j \bar{y}_j\) donde \(a_1, \ldots, a_{c}\) son constantes. Esta combinación lineal de los valores ajustados es un estimador insesgado de \(\text{E } L = \sum_{i=1}^{c} a_i (\mu + \tau_i)\).

Por lo tanto, por ejemplo, eligiendo \(a_1 = 1\) y los otros \(a_i = 0\), vemos que \(\mu + \tau_1\) es estimable. Como otro ejemplo, eligiendo \(a_1 = 1\), \(a_2 = -1\), y los otros \(a_i = 0\), vemos que \(\tau_1 - \tau_2\) es estimable. Se puede demostrar que \(\mu\) no es un parámetro estimable sin restricciones adicionales sobre \(\tau_1, \ldots, \tau_c\).