Capítulo 16 Modelos de Frecuencia-Severidad
Vista Previa del Capítulo. Muchos conjuntos de datos presentan variables dependientes con una gran proporción de ceros. Este capítulo introduce una herramienta econométrica estándar, conocida como el modelo tobit, para manejar este tipo de datos. El modelo tobit se basa en observar una variable dependiente censurada a la izquierda, como las ventas de un producto o un reclamo en una póliza de salud, donde se sabe que la variable dependiente no puede ser menor que cero. Aunque esta herramienta estándar puede ser útil, muchos conjuntos de datos actuariales con una gran proporción de ceros se modelan mejor en “dos partes”, una parte para la frecuencia y otra para la severidad. Este capítulo introduce modelos de dos partes y proporciona extensiones a un modelo de pérdida agregada, donde una unidad en estudio, como una póliza de seguro, puede resultar en más de un reclamo.
16.1 Introducción
Muchos conjuntos de datos actuariales vienen en “dos partes”:
- Una parte para la frecuencia, indicando si ha ocurrido un reclamo o, más generalmente, el número de reclamos, y
- Una parte para la severidad, indicando el monto de un reclamo.
Al predecir o estimar distribuciones de reclamos, a menudo asociamos el costo de los reclamos con dos componentes: el evento del reclamo y su monto, si ocurre. Los actuarios llaman a estos componentes frecuencia y severidad de los reclamos, respectivamente. Esta es la forma tradicional de descomponer datos de “dos partes”, donde se puede pensar en un cero como proveniente de una póliza sin reclamo (Bowers et al., 1997, Capítulo 2). Debido a esta descomposición, los modelos de dos partes también se conocen como modelos de frecuencia-severidad. Sin embargo, esta formulación tradicionalmente se ha usado sin covariables para explicar la frecuencia o la severidad. En la literatura econométrica, Cragg (1971) introdujo covariables en estos dos componentes, citando un ejemplo de seguro contra incendios.
Los datos de salud también suelen tener una gran proporción de ceros que deben ser considerados en el modelado. Los valores cero pueden representar la falta de utilización de servicios de salud por parte de un individuo, ningún gasto o no participación en un programa. En el área de la salud, Mullahy (1998) cita algunos ámbitos destacados de aplicabilidad potencial:
- Investigación de resultados - cantidad de utilización de servicios de salud o gastos.
- Demanda de servicios de salud - cantidad de servicios solicitados, como el número de visitas al médico.
- Abuso de sustancias - cantidad consumida de tabaco, alcohol y drogas ilícitas.
El aspecto de dos partes puede estar oscurecido por una forma natural de registrar datos; ingresar el monto del reclamo cuando ocurre (un número positivo) y un cero para la ausencia de reclamo. Es fácil pasar por alto una gran proporción de ceros, particularmente cuando el analista también está interesado en muchas covariables que pueden ayudar a explicar una variable dependiente. Como veremos en este capítulo, ignorar la naturaleza de dos partes puede llevar a un sesgo serio. Para ilustrarlo, recordemos del Capítulo 6 un gráfico de los ingresos de un individuo (\(x\)) frente a la cantidad de seguro adquirido (\(y\)) (Figura 6.3). Ajustar una sola línea a estos datos desinformaría a los usuarios sobre los efectos de \(x\) en \(y\).
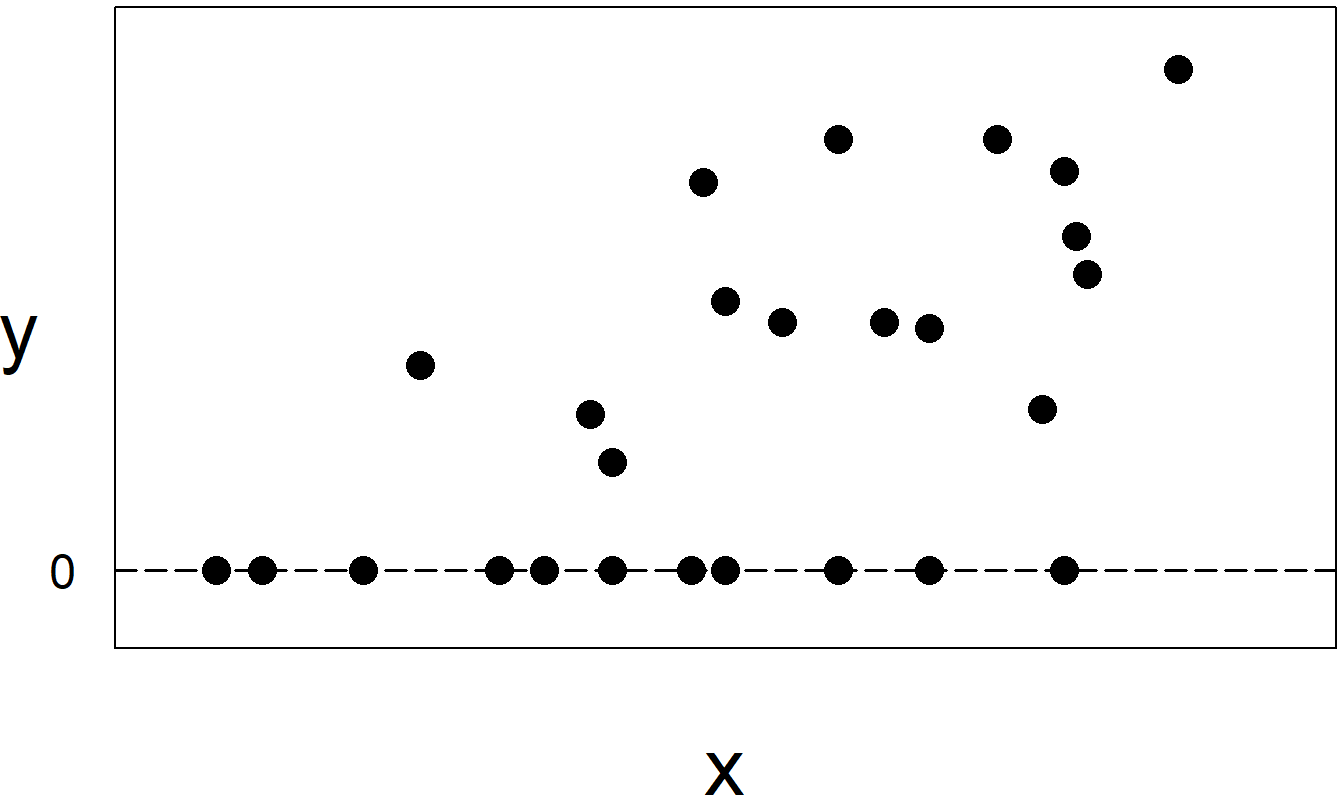
Figura 16.1: Cuando los individuos no compran seguros, se registran como ventas \(y=0\). La muestra en este gráfico representa dos submuestras, aquellos que compraron seguro, correspondientes a \(y>0\), y aquellos que no lo hicieron, correspondientes a \(y=0\).
En contraste, muchas aseguradoras mantienen archivos separados para la frecuencia y la severidad. Por ejemplo, las aseguradoras mantienen un archivo de “titulares de pólizas” que se establece cuando se suscribe una póliza. Este archivo registra mucha información de suscripción sobre los asegurados, como edad, género y experiencia previa de reclamos, información de la póliza como coberturas, deducibles y limitaciones, así como el evento del reclamo. Un archivo separado, a menudo conocido como el archivo de “reclamos”, registra detalles del reclamo contra la aseguradora, incluyendo el monto. (También puede haber un archivo de “pagos” que registre el momento de los pagos, aunque no trataremos este aquí). Este proceso de registro hace que sea natural para las aseguradoras modelar la frecuencia y la severidad como procesos separados.
16.2 Modelo Tobit
Una forma de modelar una gran proporción de ceros es asumir que la variable dependiente está censurada a la izquierda en cero. Este capítulo introduce la regresión censurada a la izquierda, comenzando con el conocido modelo tobit basado en el trabajo pionero de James Tobin (1958). Posteriormente, Goldberger (1964) acuñó la frase “modelo tobit,” reconociendo el trabajo de Tobin y su similitud con el modelo probit.
Al igual que con el modelo probit (y otros modelos de respuesta binaria), utilizamos una variable no observada, o latente, \(y^{\ast}\) que se asume que sigue un modelo de regresión lineal de la forma \[ y_i^{\ast} = \mathbf{x}_i^{\prime} \boldsymbol{\beta} + \varepsilon_i. \tag{16.1} \] Las respuestas están censuradas o “limitadas” en el sentido de que observamos \(y_i = \max \left( y_i^{\ast},d_i\right)\). El valor límite, \(d_i\), es una cantidad conocida. Muchas aplicaciones utilizan \(d_i=0\), correspondiente a ventas o gastos de cero, dependiendo de la aplicación. Sin embargo, también podríamos usar \(d_i\) para los gastos diarios reclamados como reembolso de viajes y permitir que el reembolso (como 50 o 100) varíe según el empleado \(i\). Algunos lectores pueden revisar la Sección 14.2 para una introducción al censurado.
Los parámetros del modelo consisten en los coeficientes de regresión, \(\boldsymbol{\beta}\), y el término de variabilidad, \(\sigma^2 = \mathrm{Var}~\varepsilon_i\). Con la ecuación (16.1), interpretamos los coeficientes de regresión como el cambio marginal en \(\mathrm{E~}y^{\ast}\) por unidad de cambio en cada variable explicativa. Esto puede ser satisfactorio en algunas aplicaciones, como cuando \(y^{\ast}\) representa una pérdida de seguro. Sin embargo, para la mayoría de las aplicaciones, los usuarios están típicamente interesados en cambios marginales en \(\mathrm{E~}y\), es decir, el valor esperado de la respuesta observada.
Para interpretar estos cambios marginales, es habitual adoptar la suposición de normalidad para la variable latente \(y_i^{\ast}\) (o equivalentemente para la perturbación \(\varepsilon_i\)). Con esta suposición, cálculos estándar (ver Ejercicio 16.1) muestran que \[ \mathrm{E~}y_i = d_i + \Phi \left( \frac{\mathbf{x}_i^{\prime} \boldsymbol{\beta} - d_i}{\sigma}\right) \left( \mathbf{x}_i^{\prime} \boldsymbol{\beta} - d_i + \sigma \lambda_i\right), \tag{16.2} \] donde \[ \lambda_i = \frac{\mathrm{\phi}\left( \left(\mathbf{x}_i^{\prime} \boldsymbol{\beta} - d_i\right)/\sigma \right)}{\Phi\left( \left(\mathbf{x}_i^{\prime} \boldsymbol{\beta} - d_i\right)/\sigma \right)}. \] Aquí, \(\mathrm{\phi}(\cdot)\) y \(\Phi(\cdot)\) son la función de densidad y la función de distribución de la normal estándar, respectivamente. La razón entre una función de densidad de probabilidad y una función de distribución acumulativa a veces se llama razón de Mills inversa. Aunque compleja en apariencia, la ecuación (16.2) permite calcular fácilmente \(\mathrm{E~} y\). Para valores grandes de \(\left(\mathbf{x}_i^{\prime}\boldsymbol{\beta} - d_i\right)/\sigma\), vemos que \(\lambda_i\) se aproxima a 0 y \(\Phi\left( \left(\mathbf{x}_i^{\prime}\boldsymbol{\beta} - d_i\right)/\sigma \right)\) se aproxima a 1. Interpretamos esto como que, para valores grandes del componente sistemático \(\mathbf{x}_i^{\prime}\boldsymbol{\beta}\), la función de regresión \(\mathrm{E~}y_i\) tiende a ser lineal y se aplican las interpretaciones habituales. La especificación del modelo tobit tiene el mayor impacto en las observaciones cercanas al valor límite \(d_i\).
La ecuación (16.2) muestra que, si un analista ignora los efectos del censurado, la función de regresión puede ser muy diferente de la típica función de regresión lineal, \(\mathrm{E~}y=\mathbf{x}^{\prime}\boldsymbol{\beta}\), lo que resulta en estimaciones sesgadas de los coeficientes. La otra vía tentadora es excluir observaciones limitadas (\(y_i=d_i\)) del conjunto de datos y nuevamente realizar una regresión ordinaria. Sin embargo, cálculos estándar también muestran que
\[ \mathrm{E~}\left( y_i|\ y_i>d_i\right) =\mathbf{x}_i^{\prime}\boldsymbol{\beta} + \sigma \frac{\mathrm{\phi}\left( (\mathbf{x}_i^{\prime} \boldsymbol{\beta} - d_i)/\sigma \right)}{1-\Phi \left( (\mathbf{x}_i^{\prime} \boldsymbol{\beta} - d_i)/\sigma \right)} \tag{16.3} \]
Por lo tanto, este procedimiento también resulta en coeficientes de regresión sesgados.
Un método comúnmente utilizado para estimar el modelo tobit es el de máxima verosimilitud. Empleando la suposición de normalidad, los cálculos estándar muestran que la log-verosimilitud puede expresarse como
\[ \begin{array}{ll} \ln L &= \sum\limits_{i:y_i=d_i} \ln \left\{ 1-\Phi \left( \frac{\mathbf{x}_i^{\prime}\boldsymbol{\beta} - d_i}{\sigma}\right) \right\} \\ & - \frac{1}{2} \sum\limits_{i:y_i>d_i} \left\{ \ln 2\pi \sigma^2 + \frac{(y_i-(\mathbf{x}_i^{\prime}\boldsymbol{\beta}-d_i))^2}{\sigma^2}\right\}, \tag{16.4} \end{array} \]
donde \(\{i:y_i=d_i\}\) y \(\{i:y_i>d_i\}\) indican la suma sobre las observaciones censuradas y no censuradas, respectivamente. Muchos paquetes de software estadístico pueden calcular fácilmente los estimadores de máxima verosimilitud, \(\mathbf{b}_{MLE}\) y \(s_{MLE}\), así como los errores estándar correspondientes. La Sección 11.9 introduce la inferencia por verosimilitud.
Para algunos usuarios, resulta conveniente disponer de un algoritmo que no dependa de software especializado. Un algoritmo en dos etapas, propuesto por Heckman (1976), satisface esta necesidad. Para este algoritmo, primero se resta \(d_i\) de cada \(y_i\), de modo que \(d_i\) pueda considerarse cero sin pérdida de generalidad. Incluso para aquellos que desean utilizar los estimadores de máxima verosimilitud más eficientes, el algoritmo de Heckman puede ser útil en la etapa de exploración del modelo, ya que utiliza regresión lineal para ayudar a seleccionar la forma adecuada de la ecuación de regresión.
Algoritmo de Heckman para Estimar los Parámetros del Modelo Tobit
En la primera etapa, defina la variable binaria \[ r_i=\left\{ \begin{array}{ll} 1 & \text{si } y_i>0 \\ 0 & \text{si } y_i=0 \end{array} \right. , \] indicando si la observación está censurada o no. Realice una regresión probit utilizando \(r_i\) como la variable dependiente y \(\mathbf{x}_i\) como variables explicativas. Llame a los coeficientes de regresión resultantes \(\mathbf{g}_{PROBIT}\).
Para cada observación, calcule la variable estimada \[ \widehat{\lambda}_i=\frac{\mathrm{\phi }\left( \mathbf{x}_i^{\prime} \mathbf{g}_{PROBIT}\right) }{\Phi \left( \mathbf{x}_i^{\prime} \mathbf{g}_{PROBIT}\right) }, \] una razón de Mills inversa. Con esto, realice una regresión de \(y_i\) sobre \(\mathbf{x}_i\) y \(\widehat{\lambda}_i\). Llame a los coeficientes de regresión resultantes \(\mathbf{b}_{2SLS}\).
La idea detrás de este algoritmo es que la ecuación (16.1) tiene la misma forma que el modelo probit; por lo tanto, se pueden calcular estimaciones consistentes de los coeficientes de regresión (hasta la escala). Los coeficientes de regresión \(\mathbf{b}_{2SLS}\) proporcionan estimaciones consistentes y asintóticamente normales de \(\boldsymbol{\beta}\). Sin embargo, son menos eficientes en comparación con los estimadores de máxima verosimilitud, \(\mathbf{b}_{MLE}\). Los cálculos estándar (ver Ejercicio 16.1) muestran que \(\mathrm{Var~}\left( y_i|\ y_i>d_i\right)\) depende de \(i\) (incluso cuando \(d_i\) es constante). Por lo tanto, es habitual utilizar errores estándar consistentes con heterocedasticidad para \(\mathbf{b}_{2SLS}\).
16.3 Aplicación: Gastos Médicos
Esta sección considera datos del Medical Expenditure Panel Survey (MEPS), introducidos en la Sección 11.4. Recordemos que MEPS es una encuesta probabilística que proporciona estimaciones representativas a nivel nacional sobre el uso de atención médica, gastos, fuentes de pago y cobertura de seguros para la población civil de los Estados Unidos. Consideramos datos del MEPS del primer panel de 2003 y tomamos una muestra aleatoria de \(n=2,000\) individuos entre 18 y 65 años. La Sección 11.4 analizó el componente de frecuencia, tratando de entender los determinantes que influyen en si las personas fueron hospitalizadas o no. La Sección 13.4 analizó el componente de severidad; dado que una persona fue hospitalizada, ¿cuáles son los determinantes de los gastos médicos? Este capítulo busca unificar estos dos componentes en un solo modelo de utilización de atención médica.
Estadísticas Resumidas
Tabla 16.1 revisa estas variables explicativas y proporciona estadísticas resumidas que sugieren sus efectos sobre los gastos de visitas hospitalarias. La segunda columna, “Promedio Gastos”, muestra el promedio de los gastos logarítmicos por variable explicativa, tratando los casos sin gastos como un gasto (logarítmico) de cero. Este sería el principal interés si no se descompusiera el gasto total en un valor discreto de cero y una cantidad continua.
Examinando este promedio general (logarítmico) de gastos, vemos que las mujeres tuvieron mayores gastos que los hombres. En términos de etnicidad, los nativos americanos y asiáticos tuvieron los gastos promedio más bajos. Sin embargo, estos dos grupos étnicos representaron solo el 5.4% del tamaño total de la muestra. Respecto a las regiones, parece que las personas del oeste tuvieron los gastos promedio más bajos. En términos de educación, las personas más educadas tuvieron menores gastos, lo que respalda la teoría de que las personas más educadas toman un papel más activo en mantener su salud. En cuanto a la autoevaluación de la salud, una peor salud física, mental y limitaciones relacionadas con la actividad llevaron a mayores gastos. Las personas de ingresos más bajos tuvieron mayores gastos, y aquellas con cobertura de seguro tuvieron mayores gastos promedio.
Tabla 16.1 también describe los efectos de las variables explicativas sobre la frecuencia de uso y el promedio de gastos para quienes utilizaron servicios hospitalarios. Como en la Tabla 11.4, la columna “Porcentaje Positivos Gastos” muestra el porcentaje de individuos que tuvieron algún gasto positivo, por variable explicativa. La columna “Promedio Positivos Gastos” muestra el promedio (logarítmico) de gastos en los casos donde hubo un gasto, ignorando los ceros. Esto es comparable al gasto mediano en la Tabla 13.5 (dado en dólares, no en logaritmos).
Para ilustrar, consideremos que las mujeres tuvieron mayores gastos promedio que los hombres observando la columna “Promedio Gastos”. Al desglosar esto en frecuencia y monto de utilización, vemos que las mujeres tuvieron una mayor frecuencia de utilización, pero cuando tuvieron una utilización positiva, el promedio (logarítmico) de gastos fue menor que el de los hombres. Un examen de la Tabla 16.1 muestra que esta observación se mantiene para otras variables explicativas. El efecto de una variable sobre los gastos generales puede ser positivo, negativo o no significativo; este efecto puede ser bastante diferente cuando descomponemos los gastos en componentes de frecuencia y monto.
Tabla 16.2 compara la regresión de mínimos cuadrados ordinarios (OLS) con las estimaciones de máxima verosimilitud para el modelo tobit. De esta tabla, podemos ver que hay un acuerdo sustancial entre los valores-\(t\) de estos modelos ajustados. Este acuerdo proviene de examinar el signo (positivo o negativo) y la magnitud (como superar dos para significancia estadística) del valor-\(t\) de cada variable. Los coeficientes de regresión también coinciden en gran medida en el signo. Sin embargo, no es sorprendente que las magnitudes de los coeficientes de regresión difieran sustancialmente. Esto se debe a que, según la ecuación (16.2), podemos ver que los coeficientes tobit miden el cambio marginal de la variable latente esperada \(y^{\ast}\), no el cambio marginal de la variable observada esperada \(y\), como lo hace OLS.
Tabla 16.1. Porcentaje de Gastos Positivos y Gasto Promedio Logarítmico, por Variable Explicativa
\[ \scriptsize{ \begin{array}{lllrrrr}\hline \text{Categoría} & \text{Variable} & \text{Descripción} & \text{Porcentaje} & \text{Promedio} & \text{Porcentaje} & \text{Promedio} \\ & & & \text{de datos} & \text{Gastos} & \text{Positivos} & \text{Positivos} \\ & & & & & \text{Gastos} & \text{Gastos} \\ \hline \text{Demografía} & AGE & \text{Edad en años} \\ & & \ \ \ \text{18 a 65 (promedio: 39.0)} \\ & GENDER & \text{1 si es mujer} & 52.7 & 0.91 & 10.7 & 8.53 \\ & GENDER & \text{0 si es hombre} & 47.3 & 0.40 & 4.7 & 8.66 \\ \text{Etnicidad} & ASIAN & \text{1 si es asiático} & 4.3 & 0.37 & 4.7 & 7.98 \\ & BLACK & \text{1 si es negro} & 14.8 & 0.90 & 10.5 & 8.60 \\ & NATIVE & \text{1 si es nativo} & 1.1 & 1.06 & 13.6 & 7.79 \\ & WHITE & \text{Nivel de referencia} & 79.9 & 0.64 & 7.5 & 8.59 \\ \text{Región} & NORTHEAST & \text{1 si es noreste} & 14.3 & 0.83 & 10.1 & 8.17 \\ & MIDWEST & \text{1 si es medio oeste} & 19.7 & 0.76 & 8.7 & 8.79 \\ & SOUTH & \text{1 si es sur} & 38.2 & 0.72 & 8.4 & 8.65 \\ & WEST & \text{Nivel de referencia} & 27.9 & 0.46 & 5.4 & 8.51 \\ \hline \text{Educación} & COLLEGE & \text{1 si tiene título universitario o superior} & 27.2 & 0.58 & 6.8 & 8.50 \\ & HIGHSCHOOL & \text{1 si tiene diploma de secundaria} & 43.3 & 0.67 & 7.9 & 8.54 \\ & & \text{Nivel de referencia es menor} & 29.5 & 0.76 & 8.8 & 8.64 \\ & & \ \ \ \text{que diploma de secundaria} & & & & \\ \hline \text{Autoevaluación} & POOR & \text{1 si pobre} & 3.8 & 3.26 & 36.0 & 9.07 \\ ~~\text{salud física} & FAIR & \text{1 si regular} & 9.9 & 0.66 & 8.1 & 8.12 \\ & GOOD & \text{1 si buena} & 29.9 & 0.70 & 8.2 & 8.56 \\ & VGOOD & 1 \text{si muy buena} & 31.1 & 0.54 & 6.3 & 8.64 \\ & & \text{Nivel de referencia es excelente} & 25.4 & 0.42 & 5.1 & 8.22 \\ \text{Autoevaluación} & MNHPOOR & \text{1 si salud mental pobre o regular} & 7.5 & 1.45 & 16.8 & 8.67 \\ ~~\text{salud mental} & & \text{0 si buena a excelente} & 92.5 & 0.61 & 7.1 & 8.55 \\ \text{Limitación} & ANYLIMIT & \text{1 si hay limitación funcional o actividad} & 22.3 & 1.29 & 14.6 & 8.85 \\ ~~\text{de actividad} & & \text{0 si no hay limitación} & 77.7 & 0.50 & 5.9 & 8.36 \\ \hline \text{Ingreso} & HINCOME & \text{1 si ingreso alto} & 31.6 & 0.47 & 5.4 & 8.73 \\ \text{ comparado} & MINCOME & \text{1 si ingreso medio} & 29.9 & 0.61 & 7.0 & 8.75 \\ \text{ a la línea} & LINCOME & \text{1 si ingreso bajo} & 15.8 & 0.73 & 8.3 & 8.87 \\ \text{ de pobreza} & NPOOR & \text{1 si cerca de la línea de pobreza} & 5.8 & 0.78 & 9.5 & 8.19 \\ & & \text{Nivel de referencia es pobre/negativo} & 17.0 & 1.06 & 13.0 & 8.18 \\ \hline \text{Seguro} & INSURE & 1 \text{si tiene cobertura médica pública o} & 77.8 & 0.80 & 9.2 & 8.68 \\ ~~\text{cobertura}& & ~~\text{ privada en algún mes de 2003} \\ & & \text{0 si no tiene seguro en 2003} & 22.3 & 0.23 & 3.1 & 7.43 \\ \hline \text{Total} & & & 100.0 & 0.67 & 7.9 & 8.32 \\\hline \end{array} } \]
Código R para Generar la Tabla 16.1
Tabla 16.2. Comparación de OLS, Tobit MLE y Estimaciones en Dos Etapas
\[ \scriptsize{ \begin{array}{l|rr|rr|rr} \hline & \text{OLS} & &\text{Tobit MLE} & & \text{Dos Etapas} \\ & \text{Parámetro} & & \text{Parámetro} & & \text{Parámetro} & \\ \text{Efecto} & \text{Estimación} & t\text{-ratio} & \text{Estimación} & t\text{-ratio} & \text{Estimación} & t\text{-ratio}^{\ast} \\ \hline Intercepto & -0.123 & -0.525 & -33.016 & -8.233 & 2.760 & 0.617 \\ AGE & 0.001 & 0.091 & -0.006 & -0.118 & 0.001 & 0.129 \\ GENDER & 0.379 & 3.711 & 5.727 & 4.107 & 0.271 & 1.617 \\ ASIAN & -0.115 & -0.459 & -1.732 & -0.480 & -0.091 & -0.480 \\ BLACK & 0.054 & 0.365 & 0.025 & 0.015 & 0.043 & 0.262 \\ NATIVE & 0.350 & 0.726 & 3.745 & 0.723 & 0.250 & 0.445 \\ NORTHEAST & 0.283 & 1.702 & 3.828 & 1.849 & 0.203 & 1.065 \\ MIDWEST & 0.255 & 1.693 & 3.459 & 1.790 & 0.196 & 1.143 \\ SOUTH & 0.146 & 1.133 & 1.805 & 1.056 & 0.117 & 0.937 \\ \hline COLLEGE & -0.014 & -0.089 & 0.628 & 0.329 & -0.024 & -0.149 \\ HIGHSCHOOL & -0.027 & -0.209 & -0.030 & -0.019 & -0.026 & -0.202 \\ \hline POOR & 2.297 & 7.313 & 13.352 & 4.436 & 1.780 & 1.810 \\ FAIR & -0.001 & -0.004 & 1.354 & 0.528 & -0.014 & -0.068 \\ GOOD & 0.188 & 1.346 & 2.740 & 1.480 & 0.143 & 1.018 \\ VGOOD & 0.084 & 0.622 & 1.506 & 0.815 & 0.063 & 0.533 \\ MNHPOOR & 0.000 & -0.001 & -0.482 & -0.211 & -0.011 & -0.041 \\ ANYLIMIT & 0.415 & 3.103 & 4.695 & 3.000 & 0.306 & 1.448 \\ \hline HINCOME & -0.482 & -2.716 & -6.575 & -3.035 & -0.338 & -1.290 \\ MINCOME & -0.309 & -1.868 & -4.359 & -2.241 & -0.210 & -0.952 \\ LINCOME & -0.175 & -0.976 & -3.414 & -1.619 & -0.099 & -0.438 \\ NPOOR & -0.116 & -0.478 & -2.274 & -0.790 & -0.065 & -0.243 \\ INSURE & 0.594 & 4.486 & 8.534 & 4.130 & 0.455 & 2.094 \\ \hline \text{Razón de Mill Inversa } \widehat{\lambda} & & && &-3.616 & -0.642 \\ \text{Escala } \sigma^2& 4.999 & & 14.738 & & 4.997 & \\ \hline \end{array} } \]
Nota: \(^{\ast}\) Los \(t\)-ratios en dos etapas se calculan utilizando errores estándar consistentes con heteroscedasticidad.
Código R para Generar la Tabla 16.2
Tabla 16.2 también reporta el ajuste utilizando el algoritmo de dos etapas de Heckman. El coeficiente asociado con la corrección de selección mediante la razón inversa de Mills no es estadísticamente significativo. Por lo tanto, hay un acuerdo general entre los coeficientes de OLS y los estimados utilizando el algoritmo de dos etapas. Los \(t\)-ratios de dos etapas fueron calculados usando errores estándar consistentes con heterocedasticidad, como se describe en la Sección 5.7.2. Aquí, observamos cierta discrepancia entre los \(t\)-ratios calculados con el algoritmo de Heckman y los valores de máxima verosimilitud calculados utilizando el modelo tobit. Por ejemplo, GENDER, POOR, HINCOME y MINCOME son estadísticamente significativos en el modelo tobit, pero no en el algoritmo de dos etapas. Esto resulta problemático porque ambas técnicas proporcionan estimadores consistentes siempre que se cumplan las suposiciones del modelo tobit. Por lo tanto, sospechamos de la validez de las suposiciones del modelo para estos datos; la siguiente sección presenta un modelo alternativo que resulta ser más adecuado para este conjunto de datos.
16.4 Modelo de Dos Partes
Una desventaja del modelo tobit es su dependencia de la suposición de normalidad de la respuesta latente. Una segunda, y más importante, desventaja es que una única variable latente determina tanto la magnitud de la respuesta como el truncamiento. Como señaló Cragg (1971), hay muchos casos en los que el valor límite representa una elección o actividad que está separada de la magnitud. Por ejemplo, en una población de fumadores, cero cigarrillos consumidos durante una semana puede representar simplemente un límite inferior (o límite) y puede estar influenciado por el tiempo y el dinero disponibles. Sin embargo, en una población general, cero cigarrillos consumidos durante una semana puede indicar que una persona no es fumadora, una elección que podría estar influenciada por otras decisiones de estilo de vida (donde el tiempo y el dinero pueden o no ser relevantes). Como otro ejemplo, al estudiar los gastos de atención médica, un cero representa la decisión de una persona de no utilizar servicios de salud durante un período. Para muchos estudios, la cantidad de gasto en salud está fuertemente influenciada por un proveedor de salud (como un médico); la decisión de utilizar y la cantidad de servicios de salud pueden involucrar consideraciones muy diferentes.
En la literatura actuarial tradicional (ver, por ejemplo, Bowers et al., 1997, Capítulo 2), el modelo de riesgo individual descompone una respuesta, típicamente un reclamo de seguro, en componentes de frecuencia (número) y severidad (monto). Específicamente, sea \(r_i\) una variable binaria que indica si el sujeto \(i\) tiene un reclamo de seguro y \(y_i\) describe el monto del reclamo. Entonces, el reclamo se modela como \[ \left( \text{reclamo registrado}\right)_i = r_i \times y_i. \] Esta es la base del modelo de dos partes, donde también utilizamos variables explicativas para comprender la influencia de cada componente.
Definición. Modelo de Dos Partes
Utilizar un modelo de regresión binaria con \(r_i\) como la variable dependiente y \(\mathbf{x}_{1i}\) como el conjunto de variables explicativas. Denote el conjunto correspondiente de coeficientes de regresión como \(\boldsymbol{\beta_{1}}\). Los modelos típicos incluyen probabilidad lineal, logit y probit.
Condicional a \(r_i=1\), especificar un modelo de regresión con \(y_i\) como la variable dependiente y \(\mathbf{x}_{2i}\) como el conjunto de variables explicativas. Denote el conjunto correspondiente de coeficientes de regresión como \(\boldsymbol{\beta_{2}}\). Los modelos típicos incluyen regresión lineal y regresión gamma.
A diferencia del tobit, en el modelo de dos partes no es necesario que el mismo conjunto de variables explicativas influya tanto en la frecuencia como en el monto de la respuesta. Sin embargo, generalmente hay superposición en los conjuntos de variables explicativas, donde las variables son miembros de ambos \(\mathbf{x}_{1}\) y \(\mathbf{x}_{2}\). Típicamente, se asume que \(\boldsymbol{\beta_{1}}\) y \(\boldsymbol{\beta_{2}}\) no están relacionados, de modo que la verosimilitud conjunta de los datos puede separarse en dos componentes y ejecutarse por separado, como se describe anteriormente.
Ejemplo: Datos de Gasto MEPS - Continuación. Considere los datos de gasto MEPS de la Sección 16.3 utilizando un modelo probit para la frecuencia y un modelo de regresión lineal para la severidad. Tabla 16.3 muestra los resultados de utilizar todas las variables explicativas para entender su influencia en (i) la decisión de buscar atención médica (frecuencia) y (ii) la cantidad de atención médica utilizada (severidad). A diferencia del modelo tobit de la Tabla 16.2, los modelos de dos partes permiten que cada variable tenga una influencia separada en frecuencia y severidad. Para ilustrar, los resultados del modelo completo en la Tabla 16.3 muestran que COLLEGE no tiene un impacto significativo en la frecuencia pero tiene un impacto positivo fuerte en la severidad.
Debido a la flexibilidad del modelo de dos partes, también se puede reducir la complejidad del modelo para cada componente eliminando variables innecesarias. Tabla 16.3 muestra un modelo reducido, donde se han eliminado las variables de edad y estado de salud mental del componente de frecuencia; y las variables regionales, educativas, estado físico e ingreso del componente de severidad.
Tabla 16.3. Comparación de Modelos Completos y Reducidos de Dos Partes
\[ \scriptsize{ \begin{array}{l|rr|rr|rr|rr} \hline & \text{Modelo} & & \text{Modelo}& & \text{Modelo}& &\text{Modelo} \\ & \text{Completo} & & \text{Completo}& & \text{Reducido}& &\text{ Reducido} \\ & \text{Frecuencia} & & \text{Severidad} & & \text{Frecuencia} & &\text{Severidad} \\ & \text{Parámetro} & & \text{Parámetro} & & \text{Parámetro} & & \text{Parámetro} \\ \text{Efecto} & \text{Estimación} & t\text{-ratio} & \text{Estimación} & t\text{-ratio} & \text{Estimación} & t\text{-ratio} & \text{Estimación} & t\text{-ratio} \\ \hline Intercepto & -2.263 & -10.015 & 6.828 & 13.336 & -2.281 & -11.432 & 6.879 & 14.403 \\ AGE & -0.001 & -0.154 & 0.012 & 1.368 & & & 0.020 & 2.437 \\ GENDER & 0.395 & 4.176 & -0.104 & -0.469 & 0.395 & 4.178 & -0.102 & -0.461 \\ ASIAN & -0.108 & -0.429 & -0.397 & -0.641 & -0.108 & -0.427 & -0.159 & -0.259 \\ BLACK & 0.008 & 0.062 & 0.088 & 0.362 & 0.009 & 0.073 & 0.017 & 0.072 \\ NATIVE & 0.284 & 0.778 & -0.639 & -0.905 & 0.285 & 0.780 & -1.042 & -1.501 \\ NORTHEAST & 0.283 & 1.958 & -0.649 & -2.035 & 0.281 & 1.950 & -0.778 & -2.422 \\ MIDWEST & 0.239 & 1.765 & 0.016 & 0.052 & 0.237 & 1.754 & -0.005 & -0.016 \\ SOUTH & 0.132 & 1.099 & -0.078 & -0.294 & 0.130 & 1.085 & -0.022 & -0.081 \\ \hline COLLEGE & 0.048 & 0.356 & -0.597 & -2.066 & 0.049 & 0.362 & -0.470 & -1.743 \\ HIGHSCHOOL & 0.002 & 0.017 & -0.415 & -1.745 & 0.003 & 0.030 & -0.256 & -1.134 \\ \hline POOR & 0.955 & 4.576 & 0.597 & 1.594 & 0.939 & 4.805 & & \\ FAIR & 0.087 & 0.486 & -0.211 & -0.527 & 0.079 & 0.450 & & \\ GOOD & 0.184 & 1.422 & 0.145 & 0.502 & 0.182 & 1.412 & & \\ VGOOD & 0.095 & 0.736 & 0.373 & 1.233 & 0.094 & 0.728 & & \\ MNHPOOR & -0.027 & -0.164 & -0.176 & -0.579 & & & -0.177 & -0.640 \\ ANYLIMIT & 0.318 & 2.941 & 0.235 & 0.981 & 0.311 & 3.022 & 0.245 & 1.052 \\ \hline HINCOME & -0.468 & -3.131 & 0.490 & 1.531 & -0.470 & -3.224 & & \\ MINCOME & -0.314 & -2.318 & 0.472 & 1.654 & -0.314 & -2.345 & & \\ LINCOME & -0.241 & -1.626 & 0.550 & 1.812 & -0.241 & -1.633 & & \\ NPOOR & -0.145 & -0.716 & 0.067 & 0.161 & -0.146 & -0.721 & & \\ INSURE & 0.580 & 4.154 & 1.293 & 3.944 & 0.579 & 4.147 & 1.397 & 4.195 \\ \hline \text{Escala } \sigma^2& & & 1.249 & & & & 1.333 & \\ \hline \end{array} } \]
Código R para Generar la Tabla 16.3
Modelo Tobit Tipo II
Para conectar los modelos tobit y de dos partes, asumamos que la frecuencia está representada por un modelo probit y usemos \[ r_i^{\ast}=\mathbf{x}_{1i}^{\prime}\boldsymbol \beta_{1}+\eta_{1i} \] como la tendencia latente a ser observada. Definimos \(r_i=\mathrm{I}\left( r_i^{\ast}>0\right)\) como la variable binaria que indica que se ha observado un monto. Para el componente de severidad, definimos \[ y_i^{\ast}=\mathbf{x}_{2i}^{\prime}\boldsymbol \beta_{1}+\eta_{2i} \] como la variable latente de cantidad. La cantidad “observada” es \[ y_i=\left\{ \begin{array}{ll} y_i^{\ast} & \mathrm{si~}r_i=1 \\ 0 & \mathrm{si~}r_i=0 \end{array} \right. . \] Debido a que las respuestas están censuradas, el analista está al tanto del sujeto \(i\) y tiene información de covariables incluso cuando \(r_i = 0\).
Si \(\mathbf{x}_{1i}=\mathbf{x}_{2i}\), \(\boldsymbol \beta_{1}=\boldsymbol \beta _{2}\) y \(\eta_{1i}=\eta_{2i}\), entonces esto es el marco tobit con \(d_i=0\). Si \(\boldsymbol\beta_{1}\) y \(\boldsymbol \beta_{2}\) no están relacionadas y si \(\eta_{1i}\) y \(\eta_{2i}\) son independientes, entonces esto es el marco de dos partes. Para el marco de dos partes, la verosimilitud de las respuestas observadas \(\left\{ r_i,y_i\right\}\) está dada por \[\begin{equation} L=\prod\limits_{i=1}^{n}\left\{ \left( p_i\right) ^{r_i}\left( 1-p_i\right) ^{1-r_i}\right\} \prod\limits_{r_i=1}\mathrm{\phi } \left( \frac{y_i-\mathbf{x}_{2i}^{\prime} \boldsymbol \beta_{2}}{ \sigma_{\eta 2}}\right) , \tag{16.5} \end{equation}\] donde \(p_i=\Pr \left( r_i=1\right)\) \(=\Pr \left( \mathbf{x}_{1i}^{\mathbf{ \prime }}\boldsymbol \beta_{1}+\eta_{1i}>0\right)\) \(=1-\Phi \left( -\mathbf{x}_{1i}^{\prime}\boldsymbol \beta_{1}\right)\) \(=\Phi \left( \mathbf{x} _{1i}^{\prime}\boldsymbol \beta_{1}\right)\). Asumiendo que \(\boldsymbol \beta_1\) y \(\boldsymbol \beta_2\) no están relacionadas, uno puede maximizar por separado estas dos partes de la función de verosimilitud.
En algunos casos, tiene sentido asumir que los componentes de frecuencia y severidad están relacionados. El modelo tobit considera una relación perfecta (con \(\eta_{1i}=\eta_{2i}\)) mientras que los modelos de dos partes asumen independencia. Para un modelo intermedio, el modelo tobit tipo II permite una correlación no nula entre \(\eta_{1i}\) y \(\eta_{2i}\). Ver Amemiya (1985) para más detalles. Hsiao et al. (1990) proporcionan una aplicación del modelo tobit tipo II a la cobertura de colisiones en Canadá para automóviles privados.
16.5 Modelo de Pérdidas Agregadas
Ahora consideramos modelos de dos partes donde la frecuencia puede exceder uno. Por ejemplo, si estamos rastreando accidentes automovilísticos, un asegurado puede tener más de un accidente en un año. Como otro ejemplo, podríamos estar interesados en los reclamos de una ciudad o un estado y esperar muchos reclamos por unidad gubernamental.
Para establecer la notación, para cada {\(i\)}, las respuestas observables consisten en:
- \(N_i~-\) el número de reclamos (eventos), y
- \(y_{ij},~j=1,...,N_i~-\) el monto de cada reclamo (pérdida).
Por convención, el conjunto \(\{y_{ij}\}\) está vacío cuando \(N_i=0\). Si uno usa \(N_i\) como una variable binaria, este marco se reduce a la configuración de dos partes.
Aunque tenemos información detallada sobre las pérdidas por evento, a menudo el interés se centra en las pérdidas agregadas, \(S_i=y_{i1}+...+y_{i,N_i}\). En el modelado actuarial tradicional, se asume que la distribución de las pérdidas es, condicional a la frecuencia \(N_i\), idéntica e independiente entre réplicas \(~j\). Esta representación se conoce como el modelo de riesgo colectivo, ver, por ejemplo, Klugman et al. (2008). También mantenemos esta suposición.
Los datos típicamente están disponibles en dos formas:
\(\{N_i,y_{i1},...,y_{i,N_i}\}\), por lo que está disponible información detallada sobre cada reclamo. Por ejemplo, al examinar reclamos de automóviles personales, están disponibles las pérdidas para cada reclamo. Sea \(\mathbf{y}_i=\left( y_{i1},...,y_{i,N_i}\right) ^{\prime}\) el vector de pérdidas individuales.
\(\{N_i,S_i\}\), por lo que solo están disponibles las pérdidas agregadas. Por ejemplo, al examinar pérdidas a nivel de ciudad, solo están disponibles las pérdidas agregadas.
Estamos interesados en ambas formas. Dado que hay múltiples respuestas (eventos) por sujeto {\(i\)}, uno podría abordar el análisis utilizando modelos multinivel como se describe, por ejemplo, en Raudenbush y Bryk (2002). A diferencia de una estructura multinivel, consideramos datos donde el número de eventos es aleatorio y deseamos modelarlo estocásticamente, utilizando así un marco alternativo. Cuando solo \(\{S_i\}\) está disponible, el GLM Tweedie introducido en la Sección 13.6 puede ser utilizado.
Para ver cómo modelar estos datos, consideremos la primera forma de datos. Suprimiendo el subíndice \(\{i\}\), descomponemos la distribución conjunta de las variables dependientes como: \[\begin{eqnarray*} \mathrm{f}\left( N,\mathbf{y}\right) &=&\mathrm{f}\left( N\right) ~\times ~ \mathrm{f}\left( \mathbf{y|}N\right) \\ \text{conjunta} &=&\text{frecuencia}~\times ~\text{severidad condicional,} \end{eqnarray*}\] donde \(\mathrm{f}\left( N,\mathbf{y}\right)\) denota la distribución conjunta de \(\left( N,\mathbf{y}\right)\). Esta distribución conjunta es igual al producto de los dos componentes:
- frecuencia de reclamos: \(\mathrm{f}\left( N\right)\) denota la probabilidad de tener \(N\) reclamos; y
- severidad condicional: \(\mathrm{f}\left( \mathbf{y|}N\right)\) denota la densidad condicional del vector de reclamos \(\mathbf{y}\) dado \(N\).
Representamos los componentes de frecuencia y severidad del modelo de pérdidas agregadas de la siguiente manera:
Definición. Modelo de Pérdidas Agregadas I
Usar un modelo de regresión para conteos con \(N_i\) como la variable dependiente y \(\mathbf{x}_{1i}\) como el conjunto de variables explicativas. Denotamos el conjunto correspondiente de coeficientes de regresión como \(\boldsymbol \beta_{1}\). Los modelos típicos incluyen los modelos de Poisson y binomial negativa.
Condicional a que \(N_i>0\), usar un modelo de regresión con \(y_{ij}\) como la variable dependiente y \(\mathbf{x}_{2i}\) como el conjunto de variables explicativas. Denotamos el conjunto correspondiente de coeficientes de regresión como \(\boldsymbol \beta_{2}\). Los modelos típicos incluyen la regresión lineal, la regresión gamma y los modelos lineales mixtos. Para los modelos lineales mixtos, se utiliza un intercepto específico para cada sujeto para tener en cuenta la heterogeneidad entre sujetos.
Para modelar la segunda forma de datos, el enfoque es similar. El modelo de datos de conteo en el paso 1 no cambiará. Sin embargo, el modelo de regresión en el paso 2 usará \(S_i\) como la variable dependiente. Debido a que la variable dependiente es la suma sobre \(N_i\) réplicas independientes, puede ser necesario permitir que la variabilidad dependa de \(N_i\).
Ejemplo: Datos de Gastos de MEPS - Continuación. Para obtener una idea de las observaciones empíricas de la frecuencia de reclamos, presentamos la frecuencia general de reclamos. Según esta tabla, hubo un total de 2,000 observaciones de las cuales el 92.15% no tuvieron reclamos. Hay un total de 203 (\(=1\times 130+2\times 19+3\times 2+4\times 3+5\times 2+6\times 0+7\times 1)\) reclamos.
Frecuencia de Reclamos \[ \small{ \begin{array}{l|ccccccccc} \hline \text{Cuenta} & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & \text{Total }\\ \hline \text{Número} & 1,843 & 130 & 19 & 2 & 3 & 2 & 0 & 1 & 2,000 \\ \text{Porcentaje} & 92.15 & 6.50 & 0.95 & 0.10 & 0.15 & 0.10 & 0.00 & 0.10 & 100.00 \\ \hline \end{array} } \]
Tabla 16.4 resume los ajustes de los coeficientes de regresión usando el modelo de binomial negativa. Los resultados son comparables a los modelos probit ajustados en Tabla 16.3, donde muchas de las covariables son predictores estadísticamente significativos de la frecuencia de reclamos.
Este modelo ajustado de frecuencia se basa en \(n=2,000\) personas. Los modelos de severidad ajustados en Tabla 16.4 se basan en \(n_{1}+...+n_{2000}=203\) reclamos. El modelo de regresión gamma se basa en un enlace logarítmico: \[ \mu_i=\exp \left(\mathbf{x}_i^{\prime}\boldsymbol \beta_2 \right). \]
Tabla 16.4 muestra que los resultados de ajustar un modelo de regresión ordinaria son similares a los de ajustar el modelo de regresión gamma. Son similares en el sentido de que el signo y la significancia estadística de los coeficientes para cada variable son comparables. Como se discute en el Capítulo 13, la ventaja del modelo de regresión ordinaria es su relativa simplicidad, lo que facilita su implementación e interpretación. En contraste, el modelo de regresión gamma puede ser un mejor modelo para ajustar distribuciones con colas largas como los gastos médicos.
Tabla 16.4. Modelos de Pérdidas Agregadas
\[ \scriptsize{ \begin{array}{l|rr|rr|rr} \hline & \text{Binomial} &\text{Negativa} & \text{Regresión} &\text{Ordinaria} & \text{Regresión} & \text{Gamma} \\ & \text{Frecuencia} & & \text{Severidad} & &\text{Severidad} \\ & \text{Parámetro} & & \text{Parámetro} & & \text{Parámetro} & \\ \text{Efecto} & \text{Estimación} & t\text{-ratio} & \text{Estimación} & t\text{-ratio} & \text{Estimación} & t\text{-ratio} \\ \hline Intercepto & -4.214 & -9.169 & 7.424 & 15.514 & 8.557 & 20.521 \\ AGE & -0.005 & -0.756 & -0.006 & -0.747 & -0.011 & -1.971 \\ GENDER & 0.617 & 3.351 & -0.385 & -1.952 & -0.826 & -4.780 \\ ASIAN & -0.153 & -0.306 & -0.340 & -0.588 & -0.711 & -1.396 \\ BLACK & 0.144 & 0.639 & 0.146 & 0.686 & -0.058 & -0.297 \\ NATIVE & 0.445 & 0.634 & -0.331 & -0.465 & -0.512 & -0.841 \\ NORTHEAST & 0.492 & 1.683 & -0.547 & -1.792 & -0.418 & -1.602 \\ MIDWEST & 0.619 & 2.314 & 0.303 & 1.070 & 0.589 & 2.234 \\ SOUTH & 0.391 & 1.603 & 0.108 & 0.424 & 0.302 & 1.318 \\ \hline COLLEGE & 0.023 & 0.089 & -0.789 & -2.964 & -0.826 & -3.335 \\ HIGHSCHOOL & -0.085 & -0.399 & -0.722 & -3.396 & -0.742 & -4.112 \\ \hline POOR & 1.927 & 5.211 & 0.664 & 1.964 & 0.299 & 0.989 \\ FAIR & 0.226 & 0.627 & -0.188 & -0.486 & 0.080 & 0.240 \\ GOOD & 0.385 & 1.483 & 0.223 & 0.802 & 0.185 & 0.735 \\ VGOOD & 0.348 & 1.349 & 0.429 & 1.511 & 0.184 & 0.792 \\ MNHPOOR & -0.177 & -0.583 & -0.221 & -0.816 & -0.470 & -1.877 \\ ANYLIMIT & 0.714 & 3.499 & 0.579 & 2.720 & 0.792 & 4.171 \\ \hline HINCOME & -0.622 & -2.139 & 0.723 & 2.517 & 0.557 & 2.290 \\ MINCOME & -0.482 & -1.831 & 0.720 & 2.768 & 0.694 & 3.148 \\ LINCOME & -0.460 & -1.611 & 0.631 & 2.241 & 0.889 & 3.693 \\ NPOOR & -0.465 & -1.131 & -0.056 & -0.135 & 0.217 & 0.619 \\ INSURE & 1.312 & 4.207 & 1.500 & 4.551 & 1.380 & 4.912 \\ \hline Dispersión & 2.177 & & 1.314 & & 1.131 & \\ \hline \end{array} } \]
16.6 Lecturas Adicionales y Referencias
Propiedad y Accidentes
Existe una rica literatura sobre el modelado de la distribución conjunta de frecuencia y severidad de reclamos de seguros de automóviles. Para distinguir este modelado de las aplicaciones de teoría de riesgos clásica (ver, por ejemplo, Klugman et al., 2008), nos enfocamos en casos donde hay variables explicativas disponibles, como características del titular de la póliza. Ha habido un interés sustancial en el modelado estadístico de la frecuencia de reclamos, pero la literatura sobre el modelado de la severidad de reclamos, especialmente junto con la frecuencia de reclamos, es menos extensa. Una posible explicación, señalada por Coutts (1984), es que la mayor parte de la variación en la experiencia general de reclamos puede atribuirse a la frecuencia de reclamos (al menos cuando la inflación era pequeña). Coutts (1984) también señala que el primer artículo que analizó la frecuencia y severidad de reclamos por separado parece ser Kahane y Levy (1975).
Brockman y Wright (1992) ofrecen una visión temprana de cómo el modelado estadístico de reclamos y severidad puede ser útil para la tarificación de seguros de automóviles. Por conveniencia computacional, se enfocaron en variables categóricas de tarificación para formar celdas que podrían usarse con formularios tradicionales de suscripción de seguros. Renshaw (1994) muestra cómo se pueden usar modelos lineales generalizados para analizar tanto la frecuencia como la severidad basándose en datos a nivel individual del titular de la póliza. Hsiao et al. (1990) observan el “exceso” de ceros en los datos de reclamos de titulares de pólizas (debido a la ausencia de reclamos) y comparan y contrastan los modelos Tobit, de dos partes y de ecuaciones simultáneas, basándose en el trabajo de Weisberg y Tomberlin (1982) y Weisberg et al. (1984). Todos estos artículos usan datos agrupados, no datos individuales como en este capítulo.
A nivel de titulares individuales de pólizas, Frangos y Vrontos (2001) examinaron un modelo de frecuencia y severidad de reclamos, utilizando distribuciones binomial negativa y Pareto, respectivamente. Utilizaron su modelo estadístico para desarrollar primas basadas en experiencia (bonus-malus). Pinquet (1997, 1998) proporciona un enfoque estadístico más moderno, ajustando no solo datos transversales sino también siguiendo a los titulares de pólizas a lo largo del tiempo. Pinquet estaba interesado en dos líneas de negocio, reclamos con culpa y sin culpa respecto a un tercero. Para cada línea, Pinquet hipotetizó un componente de frecuencia y severidad que se permitía correlacionar entre sí. En particular, la distribución de frecuencia de reclamos se asumió como Poisson bivariada. Las severidades se modelaron utilizando distribuciones lognormales y gamma.
Atención Médica
El modelo de dos partes se volvió prominente en la literatura de atención médica tras su adopción por parte de los investigadores del Experimento de Seguro de Salud de Rand (Duan et al, 1983, Manning et al, 1987). Utilizaron el modelo de dos partes para analizar el efecto del costo compartido del seguro de salud en la utilización y los gastos de atención médica debido a la estrecha semejanza de la demanda de atención médica con los dos procesos de toma de decisiones. Es decir, el monto de los gastos en atención médica es en gran medida independiente de la decisión del individuo de buscar tratamiento. Esto se debe a que los médicos, como agentes de los pacientes (principal), tienden a decidir la intensidad de los tratamientos según lo sugiere el modelo de principal-agente de Zweifel (1981).
El modelo de dos partes se ha convertido en una herramienta ampliamente utilizada en la literatura de atención médica a pesar de algunas críticas. Por ejemplo, Maddala (1985) argumentó que el modelado de dos partes no es apropiado para datos no experimentales debido a que la auto-selección de individuos en diferentes planes de seguro de salud es un problema. (En el Experimento de Seguro de Salud de Rand, la auto-selección no fue un problema porque los participantes fueron asignados aleatoriamente a planes de seguro de salud). Consulte Jones (2000) y Mullahy (1998) para obtener una visión general.
Los modelos de dos partes siguen siendo atractivos para modelar el uso de atención médica porque brindan información sobre los determinantes de la iniciación y el nivel de uso de atención médica. La decisión de utilizar la atención médica por parte de los individuos está relacionada principalmente con características personales, mientras que el costo por usuario puede estar más relacionado con características del proveedor de atención médica.
Código R para Generar Capítulos y Figuras
Referencias del Capítulo
- Amemiya, T. (1985). Advanced Econometrics. Harvard University Press, Cambridge, MA.
- Boucher, Jean-Philippe, Michel Denuit, and Montserratt Guillén (2006). Risk classification for claim counts: A comparative analysis of various zero-inflated mixed Poisson and hurdle models. Working paper.
- Bowers, Newton L., Hans U. Gerber, James C. Hickman, Donald A. Jones, and Cecil J. Nesbitt (1997). Actuarial Mathematics. Society of Actuaries, Schaumburg, IL.
- Brockman, M.J. and T.S. Wright. (1992). Statistical motor rating: making effective use of your data. Journal of the Institute of Actuaries 119, 457-543.
- Cameron, A. Colin and Pravin K. Trivedi. (1998) Regression Analysis of Count Data. Cambridge University Press, Cambridge.
- Coutts, S.M. (1984). Motor insurance rating, an actuarial approach. Journal of the Institute of Actuaries 111, 87-148.
- Cragg, John G. (1971). Some statistical models for limited dependent variables with application to the demand for durable goods. Econometrica 39(5), 829-844.
- Duan, Naihua, Willard G. Manning, Carl N. Morris, and Joseph P. Newhouse (1983). A comparison of alternative models for the demand for medical care. Journal of Business and Economics 1(2), 115-126.
- Frangos, Nicholas E. and Spyridon D. Vrontos (2001). Design of optimal bonus-malus systems with a frequency and a severity component on an individual basis in automobile insurance. ASTIN Bulletin 31(1), 1-22.
- Goldberger, Arthur S. (1964). Econometric Theory. John Wiley and Sons, New York.
- Heckman, James J. (1976). The common structure of statistical models of truncation, sample selection and limited dependent variables, and a simple estimator for such models. Ann. Econ. Soc. Meas. 5, 475-492.
- Hsiao, Cheng, Changseob Kim, and Grant Taylor (1990). A statistical perspective on insurance rate-making. Journal of Econometrics 44, 5-24.
- Jones, Andrew M. (2000). Health econometrics. Chapter 6 of the Handbook of Health Economics, Volume 1. Edited by Antonio J. Culyer, and Joseph P. Newhouse, Elsevier, Amsterdam. 265-344.
- Kahane, Yehuda and Haim Levy (1975). Regulation in the insurance industry: determination of premiums in automobile insurance. Journal of Risk and Insurance 42, 117-132.
- Klugman, Stuart A, Harry H. Panjer, and Gordon E. Willmot (2008). Loss Models: From Data to Decisions. John Wiley & Sons, Hoboken, New Jersey.
- Maddala, G. S. (1985). A survey of the literature on selectivity as it pertains to health care markets. Advances in Health Economics and Health Services Research 6, 3-18.
- Mullahy, John (1998). Much ado about two: Reconsidering retransformation and the two-part model in health econometrics. Journal of Health Economics 17, 247-281.
- Manning, Willard G., Joseph P. Newhouse, Naihua Duan, Emmett B. Keeler, Arleen Leibowitz, and M. Susan Marquis (1987). Health insurance and the demand for medical care: Evidence from a randomized experiment. American Economic Review 77(3), 251-277.
- Pinquet, Jean (1997). Allowance for cost of claims in bonus-malus systems. ASTIN Bulletin 27(1), 33-57.
- Pinquet, Jean (1998). Designing optimal bonus-malus systems from different types of claims. ASTIN Bulletin 28(2), 205-229.
- Raudenbush, Steven W. and Anthony S. Bryk (2002). Hierarchical Linear Models: Applications and Data Analysis Methods. (Second Edition). London: Sage.
- Tobin, James (1958). Estimation of relationships for limited dependent variables. Econometrica 26, 24-36.
- Weisberg, Herbert I. and Thomas J. Tomberlin (1982). A statistical perspective on actuarial methods for estimating pure premiums from cross-classified data. Journal of Risk and Insurance 49, 539-563.
- Weisberg, Herbert I., Thomas J. Tomberlin, and Sangit Chatterjee (1984). Predicting insurance losses under cross-classification: A comparison of alternative approaches. Journal of Business & Economic Statistics 2(2), 170-178.
- Zweifel, P. (1981). Supplier-induced demand in a model of physician behavior. In Health, Economics and Health Economics, pages 245-267. Edited by J. van der Gaag and M. Perlman, North-Holland, Amsterdam.
16.7 Ejercicios
16.1 Suponga que \(y\) sigue una distribución normal con media \(\mu\) y varianza \(\sigma^2\). Sean \(\mathrm{\phi (.)}\) y \(\Phi (.)\) la densidad y la función de distribución acumulativa normales estándar, respectivamente. Defina \(\mathrm{h} (d) = \mathrm{\phi}(d)\ \mathrm{/} \left( 1-\Phi (d)\right)\), una tasa de riesgo (hazard rate). Sea \(d\) una constante conocida y \(d_s=(d-\mu )/\sigma\) la versión estandarizada.
Determine la densidad de \(y\), condicionada a \(\{y>d\}\).
Demuestre que \(\mathrm{E}\left( y|y>d\right) = \mu + \sigma\mathrm{h}( d_s).\)
Demuestre que \(\mathrm{E\ }\left( y|y\leq d\right) =\mu -\sigma\mathrm{\phi}(d)\ \mathrm{/} \Phi (d).\)
Demuestre que \(\mathrm{Var}\left( y|y>d\right) =\sigma \left(1-\delta \left( d_s\right) \right)\), donde \(\delta \left( d\right)=\mathrm{h} \left( d\right) \left( \mathrm{h} \left( d\right)-d\right) .\)
Demuestre que \(\mathrm{E\ }\max \left( y,d\right) =\left( \mu +\sigma\mathrm{h} \left( d_s\right) \right) \left( 1-\Phi (d_s)\right)+d\Phi (d_s).\)
Demuestre que \(\mathrm{E~\min }\left( y,d\right) =\mu +d-\left(\left( \mu +\sigma \mathrm{h} \left( d_s\right) \right) \left(1-\Phi (d_s)\right) +d\Phi (d_s)\right) .\)
16.2 Verifique la log-verosimilitud en la ecuación (16.4) para el modelo tobit.
16.3 Verifique la log-verosimilitud en la ecuación (16.5) para el modelo de dos partes.
16.4 Derive la log-verosimilitud para el modelo tobit tipo dos. Demuestre que su log-verosimilitud se reduce a la ecuación (16.5) en el caso de términos de perturbación no correlacionados.