Capítulo 22 Apéndices
Apéndice A1. Inferencia Estadística Básica
Vista Previa del Apéndice. Este apéndice proporciona definiciones y hechos de un curso de inferencia estadística básica que son necesarios para el estudio del análisis de regresión.
Distribuciones de Funciones de Variables Aleatorias
Estadísticas y Distribuciones Muestrales. Una estadística resume la información en una muestra y, por lo tanto, es una función de las observaciones \(y_1,\ldots,y_n\). Dado que las observaciones son realizaciones de variables aleatorias, el estudio de las distribuciones de funciones de variables aleatorias es realmente el estudio de las distribuciones de estadísticas, conocidas como distribuciones muestrales. Las combinaciones lineales de la forma \(\sum_{i=1}^n a_i y_i\) representan un tipo importante de función. Aquí, \(a_1,\ldots,a_n\) son constantes conocidas. Para comenzar, supongamos que \(y_1,\ldots,y_n\) son variables aleatorias mutuamente independientes con \(\mathrm{E~}y_i = \mu_i\) y \(\mathrm{Var~}y_i = \sigma_i^2\). Entonces, por la linealidad de las esperanzas, tenemos \[ \mathrm{E}\left( \sum_{i=1}^n a_i y_i \right) = \sum_{i=1}^n a_i \mu_i~~~\mathrm{y}~~~\mathrm{Var}\left( \sum_{i=1}^n a_i y_i \right) = \sum_{i=1}^n a_i^2 \sigma_i^2. \] Un teorema importante en la estadística matemática es que, si cada variable aleatoria se distribuye normalmente, entonces las combinaciones lineales también se distribuyen normalmente. Es decir, tenemos:
Linealidad de Variables Aleatorias Normales. Supongamos que \(y_1,\ldots,y_n\) son variables aleatorias mutuamente independientes con \(y_i \sim N(\mu_i,\sigma_i^2)\). (Lea “\(\sim\)” como “se distribuye como”). Entonces, \[ \sum_{i=1}^n a_i y_i \sim N\left( \sum_{i=1}^n a_i \mu_i, \sum_{i=1}^n a_i^2 \sigma_i^2 \right) . \] Hay varias aplicaciones de esta propiedad importante. Primero, se puede verificar que si \(y \sim N(\mu ,\sigma^2)\), entonces \((y - \mu)/\sigma \sim N(0,1)\). En segundo lugar, supongamos que \(y_1,\ldots,y_n\) son idénticamente e independientemente distribuidos (i.i.d.) como \(N(\mu, \sigma^2)\) y tomamos \(a_i = n^{-1}\). Entonces, tenemos \[ \overline{y} = \frac{1}{n}\sum_{i=1}^n y_i \sim N\left( \mu ,\frac{\sigma^2}{n}\right) . \] Equivalente a esto, \(\sqrt{n}\left( \overline{y}-\mu \right) /\sigma\) es normal estándar.
Por lo tanto, la importante estadística muestral \(\overline{y}\) tiene una distribución normal. Además, también se puede calcular la distribución de la varianza muestral \(s_y^2\). Para \(y_1,\ldots,y_n\) que son i.i.d. \(N(\mu ,\sigma^2)\), tenemos que \(\left( n-1\right) s_y^2 /\sigma^2\sim \chi_{n-1}^2\), una distribución \(\chi^2\) (chi-cuadrado) con \(n-1\) grados de libertad. Además, \(\overline{y}\) es independiente de \(s_y^2\). A partir de estos dos resultados, tenemos que \[ \frac{\sqrt{n}}{s_y}\left( \overline{y}-\mu \right) \sim t_{n-1}, \] una distribución \(t\) con \(n-1\) grados de libertad.
Estimación y Predicción
Supongamos que \(y_1,\ldots,y_n\) son variables aleatorias i.i.d. de una distribución que se puede resumir mediante un parámetro desconocido \(\theta\). Nos interesa la calidad de una estimación de \(\theta\) y denotamos \(\widehat{\theta}\) como este estimador. Por ejemplo, consideramos \(\theta = \mu\) con \(\widehat{\theta} = \overline{y}\) y \(\theta = \sigma^2\) con \(\widehat{\theta} = s_y^2\) como nuestros principales ejemplos.
Estimación Puntual e Imparcialidad. Dado que \(\widehat{\theta}\) proporciona una aproximación (única) de \(\theta\), se le conoce como una estimación puntual de \(\theta\). Como estadística, \(\widehat{\theta}\) es una función de las observaciones \(y_1,\ldots,y_n\) que varía de una muestra a otra. Por lo tanto, los valores de \(\widehat{\theta}\) varían de una muestra a otra. Para examinar qué tan cerca tiende a estar \(\widehat{\theta}\) de \(\theta\), examinamos varias propiedades de \(\widehat{\theta}\), en particular, el sesgo y la consistencia. Se dice que un estimador puntual \(\widehat{\theta}\) es un estimador imparcial de \(\theta\) si \(\mathrm{E~}\widehat{\theta} = \theta\). Por ejemplo, dado que \(\mathrm{E~}\overline{y} = \mu\), \(\overline{y}\) es un estimador imparcial de \(\mu\).
Propiedades de Muestras Finitas versus Propiedades de Muestras Grandes de los Estimadores. Se dice que el sesgo es una propiedad de muestra finita ya que es válida para cada tamaño de muestra \(n\). Una propiedad límite o de muestra grande es la consistencia. La consistencia se expresa de dos maneras: consistencia débil y consistencia fuerte. Se dice que un estimador es débilmente consistente si \[ \lim_{n\rightarrow \infty }\Pr \left( |\widehat{\theta }-\theta |<h\right) = 1, \] para cada \(h\) positivo. Se dice que un estimador es fuertemente consistente si \(\lim_{n\rightarrow \infty }~\widehat{\theta }=\theta\), con probabilidad uno.
Principio de Estimación de Mínimos Cuadrados. En este texto, se utilizan dos principios principales de estimación: la estimación por mínimos cuadrados y la estimación por máxima verosimilitud. Para el procedimiento de mínimos cuadrados, consideremos variables aleatorias independientes \(y_1,\ldots,y_n\) con medias \(\mathrm{E~}y_i = \mathrm{g}_i(\theta )\). Aquí, \(\mathrm{g}_i(.)\) es una función conocida excepto por \(\theta\), el parámetro desconocido. El estimador de mínimos cuadrados es el valor de \(\theta\) que minimiza la suma de cuadrados \[ \mathrm{SS}(\theta )=\sum_{i=1}^n\left( y_i-\mathrm{g}_i(\theta )\right)^2. \]
Principio de Estimación de Máxima Verosimilitud. Las estimaciones por máxima verosimilitud son los valores del parámetro que son “más probables” de haber sido producidos por los datos. Consideremos las variables aleatorias independientes \(y_1,\ldots,y_n\) con función de probabilidad \(\mathrm{f}_i(a_i,\theta )\). Aquí, \(\mathrm{f}_i(a_i,\theta )\) se interpreta como una función de masa de probabilidad para \(y_i\) discreto o una función de densidad de probabilidad para \(y_i\) continuo, evaluada en \(a_i\), la realización de \(y_i\). Se asume que la función \(\mathrm{f}_i(a_i,\theta )\) es conocida excepto por \(\theta\), el parámetro desconocido. La verosimilitud de las variables aleatorias \(y_1,\ldots,y_n\) tomando valores \(a_1,\ldots,a_n\) es \[ \mathrm{L}(\theta )=\prod\limits_{i=1}^n \mathrm{f}_i(a_i,\theta ). \]
El valor de \(\theta\) que maximiza \(\mathrm{L}(\theta )\) se llama el estimador de máxima verosimilitud.
Intervalos de Confianza. Aunque las estimaciones puntuales proporcionan una aproximación única a los parámetros, las estimaciones por intervalo proporcionan un rango que incluye parámetros con un cierto nivel de probabilidad preespecificado, o confianza. Un par de estadísticas, \(\widehat{\theta }_1\) y \(\widehat{\theta }_{2}\), proporcionan un intervalo de la forma \(\left[ \widehat{\theta }_1 < \widehat{\theta }_{2}\right]\). Este intervalo es un intervalo de confianza de \(100(1-\alpha )\%\) para \(\theta\) si \[ \Pr \left( \widehat{\theta }_1 < \theta < \widehat{\theta }_{2}\right) \geq 1-\alpha . \] Por ejemplo, supongamos que \(y_1,\ldots,y_n\) son variables aleatorias i.i.d. \(N(\mu ,\sigma^2)\). Recuerde que \(\sqrt{n}\left( \overline{y}-\mu\right) /s_y\sim t_{n-1}\). Este hecho nos permite desarrollar un intervalo de confianza de \(100(1-\alpha )\%\) para \(\mu\) de la forma \(\overline{y}\pm (t-value)s_y/ \sqrt{n}\), donde \(t-value\) es el percentil \((1-\alpha /2)^{th}\) de una distribución \(t\) con \(n-1\) grados de libertad.
Intervalos de Predicción. Los intervalos de predicción tienen la misma forma que los intervalos de confianza. Sin embargo, un intervalo de confianza proporciona un rango para un parámetro, mientras que un intervalo de predicción proporciona un rango para valores externos de las observaciones. Basado en las observaciones \(y_1,\ldots,y_n\), buscamos construir estadísticas \(\widehat{\theta }_1\) y \(\widehat{\theta }_{2}\) tal que \[ \Pr \left( \widehat{\theta }_1 < y^{\ast } < \widehat{\theta }_{2}\right) \geq 1-\alpha . \] Aquí, \(y^{\ast }\) es una observación adicional que no forma parte de la muestra.
Pruebas de Hipótesis
Hipótesis Nula y Alternativa y Estadísticos de Prueba. Un procedimiento estadístico importante implica verificar ideas sobre los parámetros. Es decir, antes de que se observen los datos, se formulan ciertas ideas sobre los parámetros. En este texto, consideramos una hipótesis nula de la forma \(H_0:\theta =\theta_0\) frente a una hipótesis alternativa. Consideramos tanto una alternativa de dos colas, \(H_{a}:\theta \neq \theta_0\), como alternativas de una cola, ya sea \(H_{a}:\theta >\theta_0\) o \(H_{a}:\theta <\theta_0\). Para elegir entre estas hipótesis competidoras, utilizamos un estadístico de prueba \(T_n\) que típicamente es una estimación puntual de \(\theta\) o una versión reescalada para ajustarse a una distribución de referencia bajo \(H_0\). Por ejemplo, para probar \(H_0:\mu =\mu_0\), a menudo usamos \(T_n= \overline{y}\) o \(T_n=\sqrt{n}\left( \overline{y}-\mu_0\right) /s_y\). Nótese que esta última opción tiene una distribución \(t_{n-1}\), bajo los supuestos de datos normales i.i.d.
Regiones de Rechazo y Nivel de Significancia. Con un estadístico en mano, ahora establecemos un criterio para decidir entre las dos hipótesis competidoras. Esto se puede hacer estableciendo una región de rechazo o región crítica. La región crítica consiste en todos los posibles resultados de \(T_n\) que nos llevan a rechazar \(H_0\) a favor de \(H_{a}\). Para especificar la región crítica, primero cuantificamos los tipos de errores que se pueden cometer en el procedimiento de toma de decisiones. Un error de Tipo I consiste en rechazar \(H_0\) falsamente y un error de Tipo II consiste en rechazar \(H_{a}\) falsamente. La probabilidad de un error de Tipo I se llama nivel de significancia. Preespecificar el nivel de significancia es a menudo suficiente para determinar la región crítica. Por ejemplo, supongamos que \(y_1,\ldots,y_n\) son i.i.d. \(N(\mu ,\sigma^2)\) y estamos interesados en decidir entre \(H_0:\mu =\mu_0\) y \(H_{a}:\mu > \mu_0\). Pensando en nuestro estadístico de prueba \(T_n=\overline{y}\), sabemos que nos gustaría rechazar \(H_0\) si \(\overline{y}\) es mayor que \(\mu_0\). La pregunta es ¿cuánto mayor? Especificando un nivel de significancia \(\alpha\), deseamos encontrar una región crítica de la forma \(\{\overline{y}>c\}\) para alguna constante \(c\). Con este fin, tenemos \[ \begin{array}{ll} \alpha &= \Pr \mathrm{(Error~Tipo~I)} = \Pr (\mathrm{Rechazar~}H_0 \mathrm{~asumiendo~} H_0:\mu =\mu_0 \mathrm{~es~verdadera)} \\ & = \Pr (\overline{y}>c) = \Pr \left(\sqrt{n}\left( \overline{y}-\mu_0\right)/s_y>\sqrt{n}\left( c-\mu_0 \right)/s_y\right) \\ &= \Pr \left(t_{n-1}>\sqrt{n}\left( c-\mu_0 \right)/s_y\right). \end{array} \]
Con \(df=n-1\) grados de libertad, tenemos que \(t-value = \sqrt{n}\left( c-\mu_0\right)/s_y\) donde el \(t-value\) es el percentil \((1-\alpha)^{th}\) de una distribución \(t\). Así, resolviendo para \(c\), nuestra región crítica es de la forma \(\{\overline{y} > \mu_0 + (t-value)/s_y/\sqrt{n}\}\).
Relación entre Intervalos de Confianza y Pruebas de Hipótesis. Cálculos similares muestran que, para probar \(H_0:\mu = \mu_0\) frente a \(H_{a}:\theta \neq \theta_0\), la región crítica es de la forma \[ \{ \overline{y} > \mu_0 + (t-value)/s_y/\sqrt{n} ~\mathrm{o~} \overline{y} < \mu_0 - (t-value)/s_y/\sqrt{n}\} . \] Aquí, el \(t\)-value es el percentil \((1-\alpha /2)^{th}\) de una distribución \(t\) con \(df=n-1\) grados de libertad. Es interesante notar que el evento de caer en esta región crítica de dos colas es equivalente al evento de que \(\mu_0\) caiga fuera del intervalo de confianza \(\overline{y}\pm (t-value)s_y/\sqrt{n}\). Esto establece el hecho de que los intervalos de confianza y las pruebas de hipótesis realmente están reportando la misma evidencia con un énfasis diferente en la interpretación de la inferencia estadística.
\(p\)-valor. Otro concepto útil en las pruebas de hipótesis es el \(p\)-valor, que es la abreviatura de valor de probabilidad. Para un conjunto de datos, un \(p\)-valor se define como el nivel de significancia más pequeño para el cual se rechazaría la hipótesis nula. El \(p\)-valor es un estadístico resumen útil para que el analista de datos lo informe, ya que permite al lector comprender la fuerza de la desviación de la hipótesis nula.
Apéndice A2. Álgebra de Matrices
Definiciones Básicas
Matriz - un arreglo rectangular de números organizados en filas y columnas (el plural de matriz es matrices).
Dimensión de la matriz - el número de filas y columnas de la matriz.
Consideremos una matriz \(\mathbf{A}\) que tiene dimensiones \(m \times k\). Sea \(a_{ij}\) el símbolo para el número en la fila \(i\) y la columna \(j\) de \(\mathbf{A}\). En general, trabajamos con matrices de la forma \[ \mathbf{A} = \left( \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1k} \\ a_{21} & a_{22} & \cdots & a_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mk} \end{array} \right) . \]
Vector - un vector (columna) es una matriz que contiene solo una fila (\(m=1\)).
Vector fila - una matriz que contiene solo una columna (\(k=1\)).
Transpuesta - la transpuesta de una matriz \(\mathbf{A}\) se define al intercambiar las filas y las columnas y se denota por \(\mathbf{A}^{\prime}\) (o \(\mathbf{A}^{\mathrm{T}}\)). Así, si \(\mathbf{A}\) tiene dimensión \(m \times k\), entonces \(\mathbf{A}^{\prime}\) tiene dimensión \(k \times m\).
Matriz cuadrada - una matriz donde el número de filas es igual al número de columnas, es decir, \(m=k\).
Elemento diagonal - el número en la fila \(r\) y columna \(r\) de una matriz cuadrada, \(r=1,2,\ldots\)
Matriz diagonal - una matriz cuadrada donde todos los números no diagonales son iguales a cero.
Matriz identidad - una matriz diagonal donde todos los elementos diagonales son iguales a uno y se denota por \(\mathbf{I}\).
Matriz simétrica - una matriz cuadrada \(\mathbf{A}\) tal que la matriz permanece sin cambios si intercambiamos los roles de las filas y las columnas, es decir, si \(\mathbf{A} = \mathbf{A}^{\prime}\). Nótese que una matriz diagonal es una matriz simétrica.
Revisión de Operaciones Básicas
Multiplicación por un escalar. Sea \(c\) un número real, llamado escalar (una matriz de \(1 \times 1\)). Multiplicar un escalar \(c\) por una matriz \(\mathbf{A}\) se denota por \(c \mathbf{A}\) y se define por \[ c\mathbf{A} = \left( \begin{array}{cccc} ca_{11} & ca_{12} & \cdots & ca_{1k} \\ ca_{21} & ca_{22} & \cdots & ca_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ ca_{m1} & ca_{m2} & \cdots & ca_{mk} \end{array} \right) . \]
Suma y resta de matrices. Sean \(\mathbf{A}\) y \(\mathbf{B}\) matrices, cada una con dimensión \(m \times k\). Utilice \(a_{ij}\) y \(b_{ij}\) para denotar los números en la fila \(i\) y columna \(j\) de \(\mathbf{A}\) y \(\mathbf{B}\), respectivamente. Entonces, la matriz \(\mathbf{C} = \mathbf{A} + \mathbf{B}\) se define como la matriz con el número \((a_{ij} + b_{ij})\) para denotar el número en la fila \(i\) y la columna \(j\). De manera similar, la matriz \(\mathbf{C} = \mathbf{A} - \mathbf{B}\) se define como la matriz con el número \((a_{ij} - b_{ij})\) para denotar los números en la fila \(i\) y la columna \(j\).
Multiplicación de matrices. Si \(\mathbf{A}\) es una matriz de dimensión \(m \times c\) y \(\mathbf{B}\) es una matriz de dimensión \(c \times k\), entonces \(\mathbf{C} = \mathbf{A} \mathbf{B}\) es una matriz de dimensión \(m \times k\). El número en la fila \(i\) y columna \(j\) de \(\mathbf{C}\) es \(\sum_{s=1}^c a_{is} b_{sj}\).
Determinante - una función de una matriz cuadrada, denotada por \(\mathrm{det}(\mathbf{A})\), o \(|\mathbf{A}|\). Para una matriz de \(1 \times 1\), el determinante es \(\mathrm{det}(\mathbf{A}) = a_{11}\). Para definir determinantes de matrices más grandes, necesitamos dos conceptos adicionales. Sea \(\mathbf{A}_{rs}\) la submatriz de dimensión \((m-1) \times (m-1)\) de \(\mathbf{A}\) definida al eliminar la fila \(r\) y la columna \(s\). Recursivamente, definimos \(\mathrm{det}(\mathbf{A}) = \sum_{s=1}^m (-1)^{r+s} a_{rs} \mathrm{det}(\mathbf{A}_{rs})\), para cualquier \(r=1,\ldots,m\). Por ejemplo, para \(m=2\), tenemos \(\mathrm{det}(\mathbf{A}) = a_{11}a_{22} - a_{12}a_{21}\).
Inversa de una matriz. En álgebra de matrices, no existe el concepto de división. En su lugar, extendemos el concepto de recíprocos de números reales. Para comenzar, supongamos que \(\mathbf{A}\) es una matriz cuadrada de dimensión \(m \times m\) tal que \(\mathrm{det}(\mathbf{A}) \neq 0\). Además, sea \(\mathbf{I}\) la matriz identidad de \(m \times m\). Si existe una matriz \(m \times m\) \(\mathbf{B}\) tal que \(\mathbf{AB = I = BA}\), entonces \(\mathbf{B}\) se llama la inversa de \(\mathbf{A}\) y se escribe como \(\mathbf{B} = \mathbf{A}^{-1}\).
Definiciones Adicionales
Vectores linealmente dependientes – un conjunto de vectores \(\mathbf{c}_{1},\ldots,\mathbf{c}_{k}\) se dice que son linealmente dependientes si uno de los vectores en el conjunto puede ser escrito como una combinación lineal de los otros.
Vectores linealmente independientes – un conjunto de vectores \(\mathbf{c}_{1},\ldots,\mathbf{c}_{k}\) se dice que son linealmente independientes si no son linealmente dependientes. Específicamente, un conjunto de vectores \(\mathbf{c}_{1},\ldots,\mathbf{c}_{k}\) se dice que son linealmente independientes si y solo si la única solución de la ecuación \(x_{1}\mathbf{c}_{1} + \ldots + x_{k}\mathbf{c}_{k} = 0\) es \(x_{1} = \ldots = x_{k} = 0\).
Rango de una matriz – el mayor número de columnas (o filas) linealmente independientes de una matriz.
Matriz singular – una matriz cuadrada \(\mathbf{A}\) tal que \(\mathrm{det}(\mathbf{A}) = 0\).
Matriz no singular – una matriz cuadrada \(\mathbf{A}\) tal que \(\mathrm{det}(\mathbf{A}) \neq 0\).
Matriz definida positiva – una matriz cuadrada simétrica \(\mathbf{A}\) tal que \(\mathbf{x}^{\prime}\mathbf{Ax} > 0\) para \(\mathbf{x} \neq 0\).
Matriz definida no negativa – una matriz cuadrada simétrica \(\mathbf{A}\) tal que \(\mathbf{x}^{\prime}\mathbf{Ax} \geq 0\) para \(\mathbf{x} \neq 0\).
Ortogonal – dos matrices \(\mathbf{A}\) y \(\mathbf{B}\) son ortogonales si \(\mathbf{A}^{\prime}\mathbf{B} = 0\), una matriz cero.
Idempotente – una matriz cuadrada tal que \(\mathbf{AA = A}\).
Traza – la suma de todos los elementos diagonales de una matriz cuadrada.
Valores propios – las soluciones del polinomio de grado \(n\) \(\mathrm{det}(\mathbf{A} - \lambda \mathbf{I}) = 0\). También conocidos como raíces características y raíces latentes.
Vector propio – un vector \(\mathbf{x}\) tal que \(\mathbf{Ax} = \lambda \mathbf{x}\), donde \(\lambda\) es un valor propio de \(\mathbf{A}\). También conocido como vector característico y vector latente.
Inversa generalizada - de una matriz \(\mathbf{A}\) es una matriz \(\mathbf{B}\) tal que \(\mathbf{ABA = A}\). Usamos la notación \(\mathbf{A}^{-}\) para denotar la inversa generalizada de \(\mathbf{A}\). En el caso de que \(\mathbf{A}\) sea invertible, entonces \(\mathbf{A}^{-}\) es única y es igual a \(\mathbf{A}^{-1}\). Aunque existen varias definiciones de inversas generalizadas, la definición anterior es suficiente para nuestros propósitos. Ver Searle (1987) para una discusión adicional de definiciones alternativas de inversas generalizadas.
Vector gradiente – un vector de derivadas parciales. Si \(\mathrm{f}(.)\) es una función del vector \(\mathbf{x} = (x_1,\ldots,x_m)^{\prime}\), entonces el vector gradiente es \(\partial \mathrm{f}(\mathbf{x})/\partial \mathbf{x}\). La fila \(i\) del vector gradiente es \(\partial \mathrm{f}(\mathbf{x})/\partial x_i\).
Matriz Hessiana – una matriz de segundas derivadas. Si \(\mathrm{f}(.)\) es una función del vector \(\mathbf{x} = (x_1,\ldots,x_m)^{\prime}\), entonces la matriz Hessiana es \(\partial^2 \mathrm{f}(\mathbf{x})/\partial \mathbf{x}\partial \mathbf{x}^{\prime}\). El elemento en la fila \(i\) y la columna \(j\) de la matriz Hessiana es \(\partial^{2}\mathrm{f}(\mathbf{x})/\partial x_i\partial x_j\).
Apéndice A3. Tablas de Probabilidad
Distribución Normal
Recuerde de la ecuación (1.1) que la función de densidad de probabilidad está definida por \[ \mathrm{f}(y) = \frac{1}{\sigma \sqrt{2\pi }}\exp \left( -\frac{1}{2\sigma^2 }\left( y-\mu \right)^2\right) \] donde \(\mu\) y \(\sigma^2\) son parámetros que describen la curva. En este caso, escribimos \(y \sim N(\mu,\sigma^2)\). Cálculos sencillos muestran que \[ \mathrm{E}~y = \int_{-\infty}^{\infty} y \mathrm{f}(y) \, dy = \int_{-\infty}^{\infty} y \frac{1}{\sigma \sqrt{2\pi }}\exp \left( -\frac{1}{2\sigma^2 }\left( y-\mu \right)^2 \right) \, dy = \mu \] y \[ \mathrm{Var}~y = \int_{-\infty}^{\infty} (y-\mu)^2 \mathrm{f}(y) \, dy = \int_{-\infty}^{\infty} (y-\mu)^2 \frac{1}{\sigma \sqrt{2\pi }}\exp \left( -\frac{1}{2\sigma^2 }\left( y-\mu \right)^2 \right) \, dy = \sigma^2 . \] Así, la notación \(y \sim N(\mu,\sigma^2)\) se interpreta como que la variable aleatoria está distribuida normalmente con media \(\mu\) y varianza \(\sigma^2\). Si \(y \sim N(0,1)\), entonces se dice que \(y\) es normal estándar.
Figura 22.1: Función de densidad de probabilidad normal estándar
| \(y\) | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.5000 | 0.5398 | 0.5793 | 0.6179 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 |
| 1 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 | 0.9641 | 0.9713 |
| 2 | 0.9772 | 0.9821 | 0.9861 | 0.9893 | 0.9918 | 0.9938 | 0.9953 | 0.9965 | 0.9974 | 0.9981 |
| 3 | 0.9987 | 0.9990 | 0.9993 | 0.9995 | 0.9997 | 0.9998 | 0.9998 | 0.9999 | 0.9999 | 1.0000 |
Notas: Las probabilidades se pueden encontrar buscando en la fila adecuada para el dígito inicial y la columna para el decimal. Por ejemplo, \(\Pr ( y \le 0.1) = 0.5398\).
Distribución Chi-Cuadrado
Distribución Chi-Cuadrado. Varias distribuciones importantes pueden vincularse a la distribución normal. Si \(y_1, \ldots, y_n\) son variables aleatorias i.i.d. tales que cada \(y_i \sim N(0,1)\), entonces se dice que \(\sum_{i=1}^n y_i^2\) tiene una distribución chi-cuadrado con parámetro \(n\). Más generalmente, una variable aleatoria \(w\) con función de densidad de probabilidad \[ \mathrm{f}(w) = \frac{2^{-k/2}}{\Gamma(k/2)} w^{k/2-1} \exp (-w/2), ~~~~~~w > 0 \] se dice que tiene una distribución chi-cuadrado con \(df = k\) grados de libertad, escrita como \(w \sim \chi_k^2\). Cálculos sencillos muestran que para \(w \sim \chi_k^2\), tenemos \(\mathrm{E}~w = k\) y \(\mathrm{Var}~w = 2k\). En general, el parámetro de grados de libertad no necesita ser un número entero, aunque lo es para las aplicaciones de este texto.
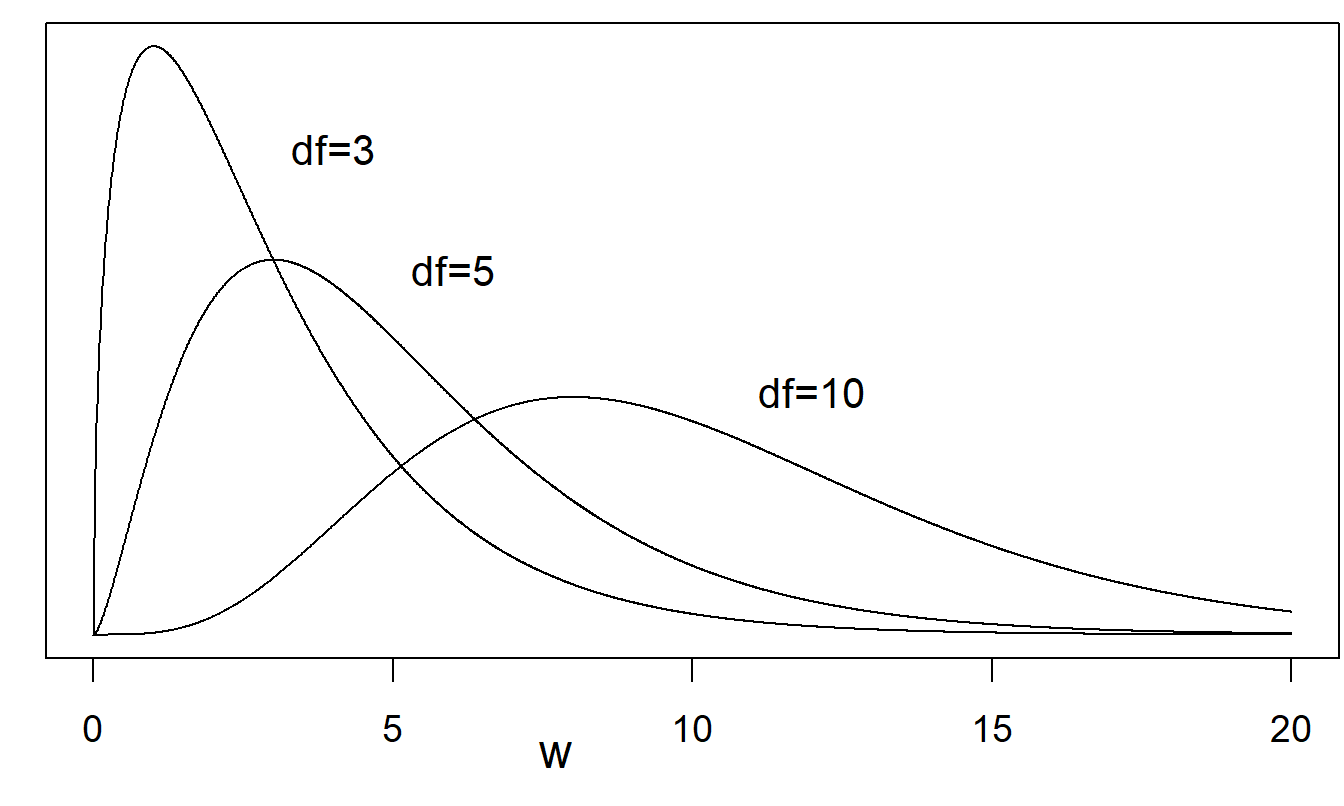
Figura 22.2: Varias funciones de densidad de probabilidad chi-cuadrado. Se muestran curvas para \(df\) = 3, \(df\) = 5, y \(df\) = 10. Un mayor número de grados de libertad conduce a curvas que son menos asimétricas.
| \(df\) | 0.6 | 0.7 | 0.8 | 0.9 | 0.95 | 0.975 | 0.99 | 0.995 | 0.9975 | 0.999 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.71 | 1.07 | 1.64 | 2.71 | 3.84 | 5.02 | 6.63 | 7.88 | 9.14 | 10.83 |
| 2 | 1.83 | 2.41 | 3.22 | 4.61 | 5.99 | 7.38 | 9.21 | 10.60 | 11.98 | 13.82 |
| 3 | 2.95 | 3.66 | 4.64 | 6.25 | 7.81 | 9.35 | 11.34 | 12.84 | 14.32 | 16.27 |
| 4 | 4.04 | 4.88 | 5.99 | 7.78 | 9.49 | 11.14 | 13.28 | 14.86 | 16.42 | 18.47 |
| 5 | 5.13 | 6.06 | 7.29 | 9.24 | 11.07 | 12.83 | 15.09 | 16.75 | 18.39 | 20.52 |
| 10 | 10.47 | 11.78 | 13.44 | 15.99 | 18.31 | 20.48 | 23.21 | 25.19 | 27.11 | 29.59 |
| 15 | 15.73 | 17.32 | 19.31 | 22.31 | 25.00 | 27.49 | 30.58 | 32.80 | 34.95 | 37.70 |
| 20 | 20.95 | 22.77 | 25.04 | 28.41 | 31.41 | 34.17 | 37.57 | 40.00 | 42.34 | 45.31 |
| 25 | 26.14 | 28.17 | 30.68 | 34.38 | 37.65 | 40.65 | 44.31 | 46.93 | 49.44 | 52.62 |
| 30 | 31.32 | 33.53 | 36.25 | 40.26 | 43.77 | 46.98 | 50.89 | 53.67 | 56.33 | 59.70 |
| 35 | 36.47 | 38.86 | 41.78 | 46.06 | 49.80 | 53.20 | 57.34 | 60.27 | 63.08 | 66.62 |
| 40 | 41.62 | 44.16 | 47.27 | 51.81 | 55.76 | 59.34 | 63.69 | 66.77 | 69.70 | 73.40 |
| 60 | 62.13 | 65.23 | 68.97 | 74.40 | 79.08 | 83.30 | 88.38 | 91.95 | 95.34 | 99.61 |
| 120 | 123.29 | 127.62 | 132.81 | 140.23 | 146.57 | 152.21 | 158.95 | 163.65 | 168.08 | 173.62 |
Distribución t
Supongamos que \(y\) y \(w\) son independientes con \(y \sim N(0,1)\) y \(w \sim \chi_k^2\). Entonces, se dice que la variable aleatoria \(t = y / \sqrt{w/k}\) tiene una distribución t con \(df = k\) grados de libertad. La función de densidad de probabilidad es \[ \mathrm{f}(t) = \frac{\Gamma \left( k+ \frac{1}{2} \right)}{\Gamma(k/2)} \left( k \pi \right)^{-1/2} \left( 1 + \frac{t^2}{k} \right)^{-(k+1/2)}, ~~~~~~-\infty < t < \infty \] Esto tiene media 0, para \(k > 1\), y varianza \(k/(k-2)\) para \(k > 2\).
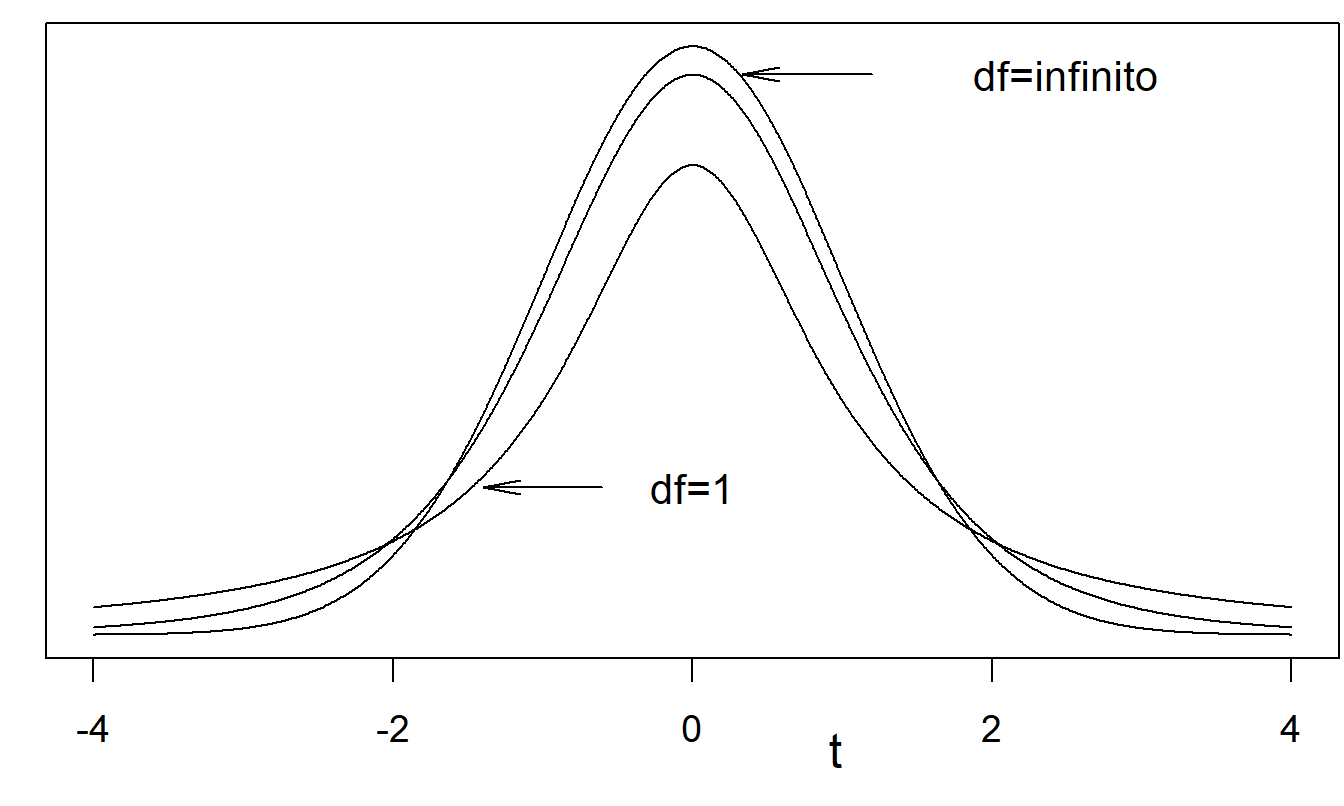
Figura 22.3: Varias funciones de densidad de probabilidad de la distribución t. La distribución t con \(df = \infty\) es la distribución normal estándar. Se muestran curvas para \(df = 1\), \(df = 5\) (no etiquetado) y \(df = ∞\). Un menor \(df\) significa colas más gruesas.
| \(df\) | 0.6 | 0.7 | 0.8 | 0.9 | 0.95 | 0.975 | 0.99 | 0.995 | 0.9975 | 0.999 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.325 | 0.727 | 1.376 | 3.078 | 6.314 | 12.706 | 31.821 | 63.657 | 127.321 | 318.309 |
| 2 | 0.289 | 0.617 | 1.061 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 14.089 | 22.327 |
| 3 | 0.277 | 0.584 | 0.978 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 7.453 | 10.215 |
| 4 | 0.271 | 0.569 | 0.941 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 5.598 | 7.173 |
| 5 | 0.267 | 0.559 | 0.920 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 4.773 | 5.893 |
| 10 | 0.260 | 0.542 | 0.879 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 3.581 | 4.144 |
| 15 | 0.258 | 0.536 | 0.866 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.286 | 3.733 |
| 20 | 0.257 | 0.533 | 0.860 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.153 | 3.552 |
| 25 | 0.256 | 0.531 | 0.856 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.078 | 3.450 |
| 30 | 0.256 | 0.530 | 0.854 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.030 | 3.385 |
| 35 | 0.255 | 0.529 | 0.852 | 1.306 | 1.690 | 2.030 | 2.438 | 2.724 | 2.996 | 3.340 |
| 40 | 0.255 | 0.529 | 0.851 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 2.971 | 3.307 |
| 60 | 0.254 | 0.527 | 0.848 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 2.915 | 3.232 |
| 120 | 0.254 | 0.526 | 0.845 | 1.289 | 1.658 | 1.980 | 2.358 | 2.617 | 2.860 | 3.160 |
| ∞ | 0.253 | 0.524 | 0.842 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 2.807 | 3.090 |
Distribución F
Supongamos que \(w_1\) y \(w_2\) son independientes con distribuciones \(w_1 \sim \chi_m^2\) y \(w_2 \sim \chi_n^2\). Entonces, la variable aleatoria \(F = (w_1/m) / (w_2/n)\) tiene una distribución F con parámetros \(df_1 = m\) y \(df_2 = n\), respectivamente. La función de densidad de probabilidad es \[ \mathrm{f}(y) = \frac{\Gamma \left(\frac{m+n}{2} \right)}{\Gamma(m/2)\Gamma(n/2)} \left( \frac{m}{n} \right)^{m/2} \frac{y^{(m-2)/2}} {\left( 1 + \frac{m}{n}y \right)^{m+n+2}} , ~~~~~~y > 0 \] Esto tiene media \(n/(n-2)\), para \(n > 2\), y varianza \(2n^2(m+n-2)/[m(n-2)^2(n-4)]\) para \(n > 4\).
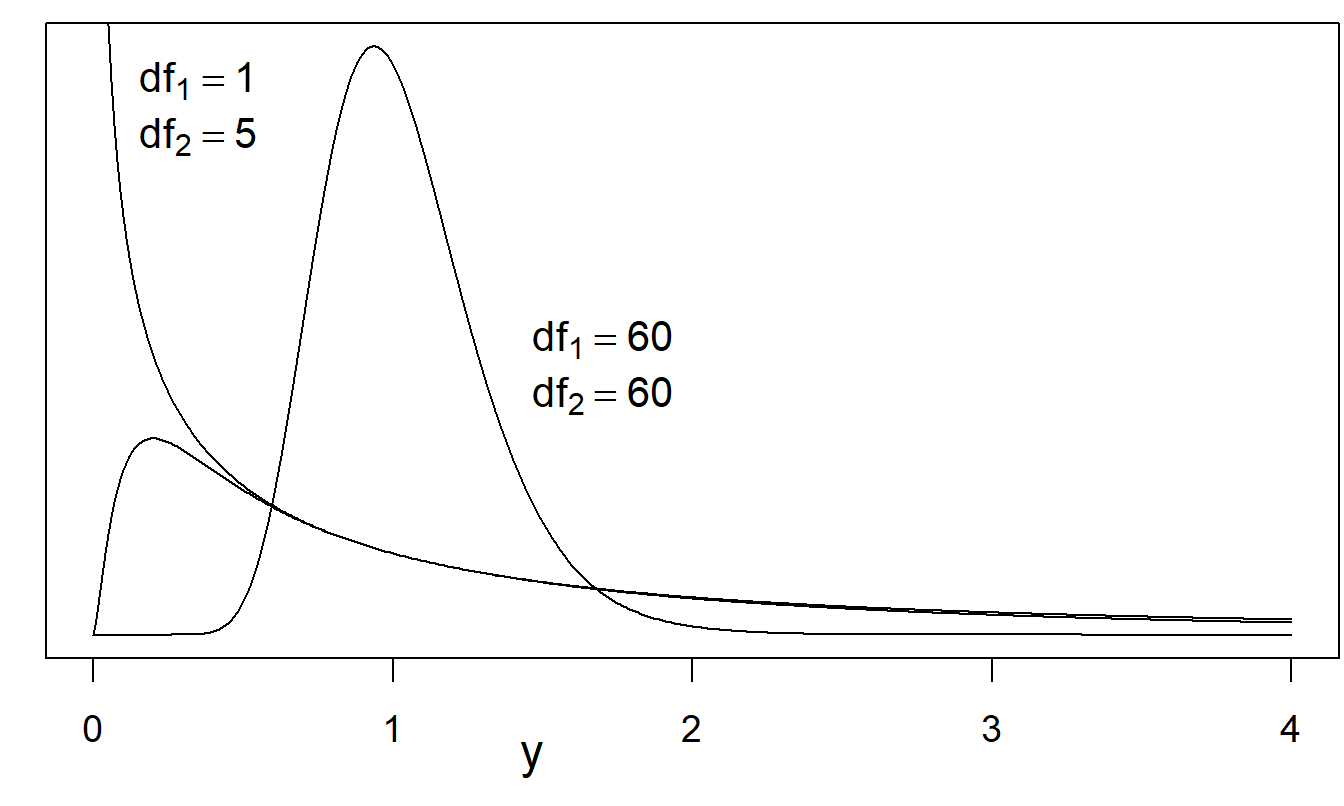
Figura 22.4: Varias funciones de densidad de probabilidad de la distribución \(F\). Se muestran curvas para (i) \(df_1\) = 1, \(df_2\) = 5, (ii) \(df_1\) = 5, \(df_2\) = 1 (no etiquetado), y (iii) \(df_1\) = 60, \(df_2\) = 60. A medida que \(df_2\) tiende a \(\infty\), la distribución \(F\) tiende a una distribución chi-cuadrado.
| \(df_1\) | 1 | 3 | 5 | 10 | 20 | 30 | 40 | 60 | 120 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 161.45 | 10.13 | 6.61 | 4.96 | 4.35 | 4.17 | 4.08 | 4.00 | 3.92 |
| 2 | 199.50 | 9.55 | 5.79 | 4.10 | 3.49 | 3.32 | 3.23 | 3.15 | 3.07 |
| 3 | 215.71 | 9.28 | 5.41 | 3.71 | 3.10 | 2.92 | 2.84 | 2.76 | 2.68 |
| 4 | 224.58 | 9.12 | 5.19 | 3.48 | 2.87 | 2.69 | 2.61 | 2.53 | 2.45 |
| 5 | 230.16 | 9.01 | 5.05 | 3.33 | 2.71 | 2.53 | 2.45 | 2.37 | 2.29 |
| 10 | 241.88 | 8.79 | 4.74 | 2.98 | 2.35 | 2.16 | 2.08 | 1.99 | 1.91 |
| 15 | 245.95 | 8.70 | 4.62 | 2.85 | 2.20 | 2.01 | 1.92 | 1.84 | 1.75 |
| 20 | 248.01 | 8.66 | 4.56 | 2.77 | 2.12 | 1.93 | 1.84 | 1.75 | 1.66 |
| 25 | 249.26 | 8.63 | 4.52 | 2.73 | 2.07 | 1.88 | 1.78 | 1.69 | 1.60 |
| 30 | 250.10 | 8.62 | 4.50 | 2.70 | 2.04 | 1.84 | 1.74 | 1.65 | 1.55 |
| 35 | 250.69 | 8.60 | 4.48 | 2.68 | 2.01 | 1.81 | 1.72 | 1.62 | 1.52 |
| 40 | 251.14 | 8.59 | 4.46 | 2.66 | 1.99 | 1.79 | 1.69 | 1.59 | 1.50 |
| 60 | 252.20 | 8.57 | 4.43 | 2.62 | 1.95 | 1.74 | 1.64 | 1.53 | 1.43 |
| 120 | 253.25 | 8.55 | 4.40 | 2.58 | 1.90 | 1.68 | 1.58 | 1.47 | 1.35 |