Capítulo 9 Pronósticos y Modelos de Series Temporales

Vista Previa del Capítulo. Este capítulo introduce dos técnicas populares de suavización, promedios móviles (corridos) y suavización exponencial, para realizar pronósticos. Estas técnicas son simples de explicar y fácilmente interpretables. También pueden expresarse como modelos de regresión, donde se utiliza la técnica de mínimos cuadrados ponderados (WLS) para calcular las estimaciones de los parámetros. Luego se presenta la estacionalidad, seguida de una discusión sobre dos temas más avanzados de series temporales, pruebas de raíces unitarias y modelos de volatilidad (ARCH/GARCH).

9.1 Suavización con Promedios Móviles

Suavizar una serie temporal con un promedio móvil, o corrido, es un procedimiento probado por el tiempo. Esta técnica sigue siendo utilizada por muchos analistas de datos debido a su facilidad de cálculo y posterior facilidad de interpretación. Como discutimos a continuación, este estimador también puede motivarse como un estimador de mínimos cuadrados ponderados (WLS). Por lo tanto, el estimador disfruta de ciertas propiedades teóricas.

El estimador de promedio móvil o corrido básico se define como: \[\begin{equation} \widehat{s}_t = \frac{y_t + y_{t-1} + \ldots + y_{t-k+1}}{k}, \tag{9.1} \end{equation}\] donde $k$ es la longitud del promedio móvil. La elección de $k$ depende de la cantidad de suavización deseada. Cuanto mayor sea el valor de $k$, más suave será la estimación $\widehat{s}_t$ porque se realiza un mayor promedio. La elección $k=1$ corresponde a no realizar suavización.

Aplicación: Componente Médico del IPC

El índice de precios al consumidor (IPC) es una canasta de bienes y servicios cuyo precio mide en los Estados Unidos la Oficina de Estadísticas Laborales. Al medir esta canasta periódicamente, los consumidores obtienen una idea del aumento constante de precios a lo largo del tiempo, lo que, entre otras cosas, sirve como un proxy para la inflación. El IPC está compuesto por muchos componentes, que reflejan la importancia relativa de cada componente para la economía en general. Aquí, estudiamos el componente médico del IPC, la parte de la canasta general que ha crecido más rápido desde 1967. Los datos que consideramos son valores trimestrales del componente médico del IPC (MCPI) durante un período de sesenta años, desde 1947 hasta el primer trimestre de 2007, inclusive. Durante este período, el índice aumentó de 13.3 a 346.0. Esto representa un aumento de 26 veces en los sesenta años, lo que se traduce en un aumento trimestral de 1.36%.

La Figura 9.1 es un gráfico de serie temporal de los cambios porcentuales trimestrales en el MCPI. Tenga en cuenta que ya hemos cambiado del índice no estacionario a cambios porcentuales. (El índice es no estacionario porque muestra un crecimiento tremendo durante el período considerado). Para ilustrar el efecto de la elección de $k$, considere los dos paneles de la Figura 9.1. En el panel superior de la Figura 9.1, la serie suavizada con $k=4$ se superpone a la serie real. El panel inferior es el gráfico correspondiente con $k=8$. Los valores ajustados en el panel inferior son menos irregulares que los del panel superior. Esto nos ayuda a identificar gráficamente las tendencias reales en la serie. El peligro de elegir un valor demasiado alto de $k$ es que podemos “sobre-suavizar” los datos y perder de vista las tendencias reales.

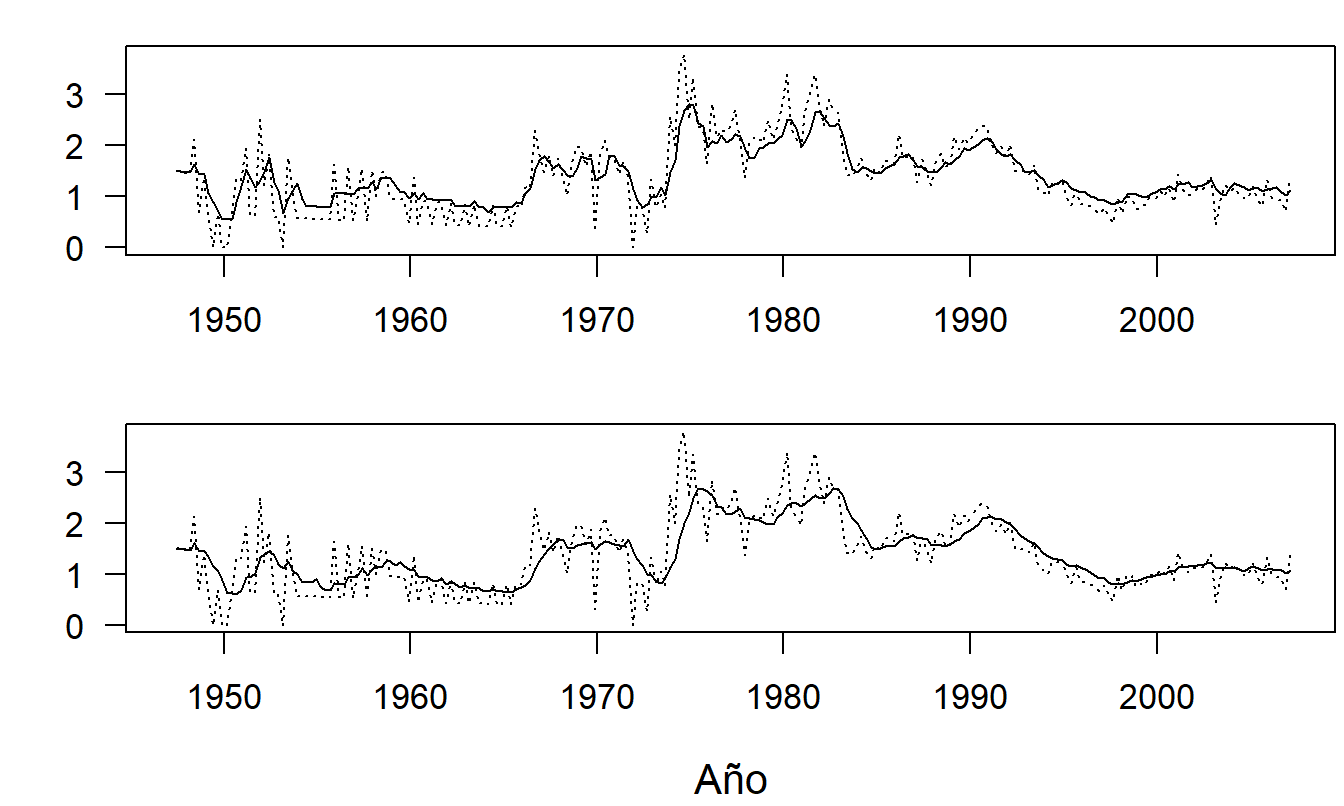
$Cambios Porcentuales Trimestrales en el Componente Médico del Índice de Precios al Consumidor. En ambos paneles, la línea discontinua es el índice. En el panel superior, la línea sólida es la versión suavizada con $k$=4. En el panel inferior, la línea sólida es la versión suavizada con $k$=8. Fuente: Oficina de Estadísticas Laborales$

Figura 9.1: Cambios Porcentuales Trimestrales en el Componente Médico del Índice de Precios al Consumidor. En ambos paneles, la línea discontinua es el índice. En el panel superior, la línea sólida es la versión suavizada con $k$=4. En el panel inferior, la línea sólida es la versión suavizada con $k$=8. Fuente: Oficina de Estadísticas Laborales

Para pronosticar la serie, reexpresamos la ecuación (9.1) recursivamente para obtener \[\begin{equation} \widehat{s}_t = \frac{y_t + y_{t-1} + \ldots + y_{t-k+1}}{k} = \frac{y_t + k \widehat{s}_{t-1} - y_{t-k}}{k} = \widehat{s}_{t-1} + \frac{y_t-y_{t-k}}{k}. \tag{9.2} \end{equation}\] Si no hay tendencias en los datos, entonces el segundo término en el lado derecho, $(y_t-y_{t-k})/k$, puede ignorarse en la práctica. Esto da como resultado la ecuación de pronóstico $\widehat{y}_{T+l} = \widehat{s}_T$ para pronósticos $l$ unidades de tiempo hacia el futuro.

Existen varias variantes de promedios móviles en la literatura. Por ejemplo, supongamos que una serie puede expresarse como $y_t = \beta_0 + \beta_1 t + \varepsilon_t$, un modelo de tendencia lineal en el tiempo. Esto puede manejarse a través del siguiente procedimiento de suavización doble:

Crear una serie suavizada utilizando la ecuación (9.1), es decir, $\widehat{s}_t^{(1)}=(y_t+\ldots+y_{t-k+1})/k.$
Crear una serie suavizada doble utilizando la ecuación (9.1) y tratando la serie suavizada creada en el paso (i) como entrada. Es decir, $\widehat{s}_t^{(2)} = (\widehat{s}_t^{(1)} + \ldots + \widehat{s}_{t-k+1}^{(1)})/k.$

Es fácil verificar que este procedimiento suaviza el efecto de una tendencia lineal en el tiempo. La estimación de la tendencia es $b_{1,T}=2\left( \widehat{s}_T^{(1)}-\widehat{s}_T^{(2)}\right) /(k-1)$. Los pronósticos resultantes son $\widehat{y}_{T+l} = \widehat{s}_T + b_{1,T}~l$ para pronósticos $l$ unidades de tiempo hacia el futuro.

Mínimos Cuadrados Ponderados

Una característica importante de los promedios móviles es que pueden expresarse como estimaciones de mínimos cuadrados ponderados (WLS). La estimación WLS se introdujo en la Sección 5.7.3. Encontrará una discusión adicional en la Sección 15.1.1. Recuerde que las estimaciones WLS minimizan una suma ponderada de cuadrados. El procedimiento WLS encuentra los valores de $b_0^{\ast}, \ldots, b_{k}^{\ast}$ que minimizan

\[\begin{equation} WSS_T\left( b_0^{\ast },\ldots, b_k^{\ast}\right) = \sum_{t=1}^{T} w_t \left( y_t-\left( b_0^{\ast} + b_1^{\ast} x_{t1}, \ldots, b_{k}^{\ast} x_{tk} \right) \right)^2. \tag{9.3} \end{equation}\] Aquí, $WSS_T$ es la suma ponderada de cuadrados en el tiempo $T$.

Para llegar a la estimación de promedio móvil, usamos el modelo $y_t = \beta_0 + \varepsilon_t$ con la elección de pesos $w_t=1$ para $t = T-k+1, \ldots, T$ y $w_t=0$ para $t<T-k+1$. Así, el problema de minimizar $WSS_T$ en la ecuación (9.3) se reduce a encontrar $b_0^{\ast}$ que minimice $\sum_{t=T-k+1}^{T}\left( y_t - b_0^{\ast} \right)^2.$ El valor de $b_0^{\ast}$ en esta expresión es $b_0 = \widehat{s}_T$, que es el promedio móvil de longitud $k$.

Este modelo, junto con esta elección de pesos, se llama un modelo de media constante local. Bajo un modelo de media constante global, se utilizan pesos iguales y la estimación de mínimos cuadrados de $\beta_0$ es el promedio total, $\overline{y}$. Bajo el modelo de media constante local, damos igual peso a las observaciones dentro de $k$ unidades de tiempo del tiempo de evaluación $T$ y peso cero a otras observaciones. Aunque es intuitivamente atractivo dar más peso a las observaciones más recientes, la idea de un corte abrupto en un $k$ algo arbitrario no es atractiva. Esta crítica se aborda utilizando la suavización exponencial, introducida en la siguiente sección.

9.2 Suavización Exponencial

Las estimaciones de suavización exponencial son promedios ponderados de valores pasados de una serie, donde los pesos se obtienen mediante una serie que disminuye exponencialmente. Para ilustrar, piense en $w$ como un número de peso entre cero y uno, y considere el promedio ponderado \[ \frac{y_t + w y_{t-1} + w^2 y_{t-2} + w^3 y_{t-3} + \ldots}{1/(1-w)}. \] Este es un promedio ponderado porque los pesos $w^k (1-w)$ suman uno, es decir, una expansión de serie geométrica da como resultado $\sum_{k=0}^{\infty }w^k = 1/(1-w)$.

Debido a que no hay observaciones disponibles en el pasado infinito, usamos la versión truncada \[\begin{equation} \widehat{s}_t = \frac{y_t + w y_{t-1} + \ldots + w^{t-1} y_1 + \ldots + w^t y_0}{1/(1-w) } \tag{9.4} \end{equation}\] para definir la estimación suavizada exponencialmente de la serie. Aquí, $y_0$ es el valor inicial de la serie y a menudo se elige como cero, $y_1$, o el valor promedio de la serie, $\overline{y}$. Al igual que las estimaciones de promedio móvil, las estimaciones suavizadas en la ecuación (9.4) proporcionan mayores pesos a observaciones más recientes en comparación con observaciones lejanas respecto al tiempo $t$. A diferencia de los promedios móviles, la función de peso es suave.

La definición de estimaciones de suavización exponencial en la ecuación (9.4) parece compleja. Sin embargo, al igual que con los promedios móviles en la ecuación (9.2), podemos reexpresar la ecuación (9.4) recursivamente para obtener \[\begin{equation} \widehat{s}_t = \widehat{s}_{t-1} + (1-w)(y_t-\widehat{s}_{t-1}) = (1-w) y_t + w \widehat{s}_{t-1}. \tag{9.5} \end{equation}\] La expresión de las estimaciones suavizadas en la ecuación (9.5) es más fácil de calcular que la definición en la ecuación (9.4).

La ecuación (9.5) también proporciona ideas sobre el rol de $w$ como el parámetro de suavización. Por ejemplo, por un lado, cuando $w$ se acerca a cero, $\widehat{s}_t$ se acerca a $y_t$. Esto indica que se ha realizado poca suavización. Por otro lado, cuando $w$ se acerca a uno, el efecto de $y_t$ en $\widehat{s}_t$ es mínimo. Esto indica que se ha realizado una gran cantidad de suavización porque el valor ajustado actual está compuesto casi en su totalidad por observaciones pasadas.

Ejemplo: Componente Médico del IPC - Continuación. Para ilustrar el efecto de la elección del parámetro de suavización, considere los dos paneles de la Figura 9.2. Estos son gráficos de series temporales del índice trimestral del componente médico del IPC. En el panel superior, la serie suavizada con $w=0.2$ se superpone a la serie real. El panel inferior es el gráfico correspondiente con $w=0.8$. En estas figuras, podemos observar que cuanto mayor es $w$, más suaves son los valores ajustados.

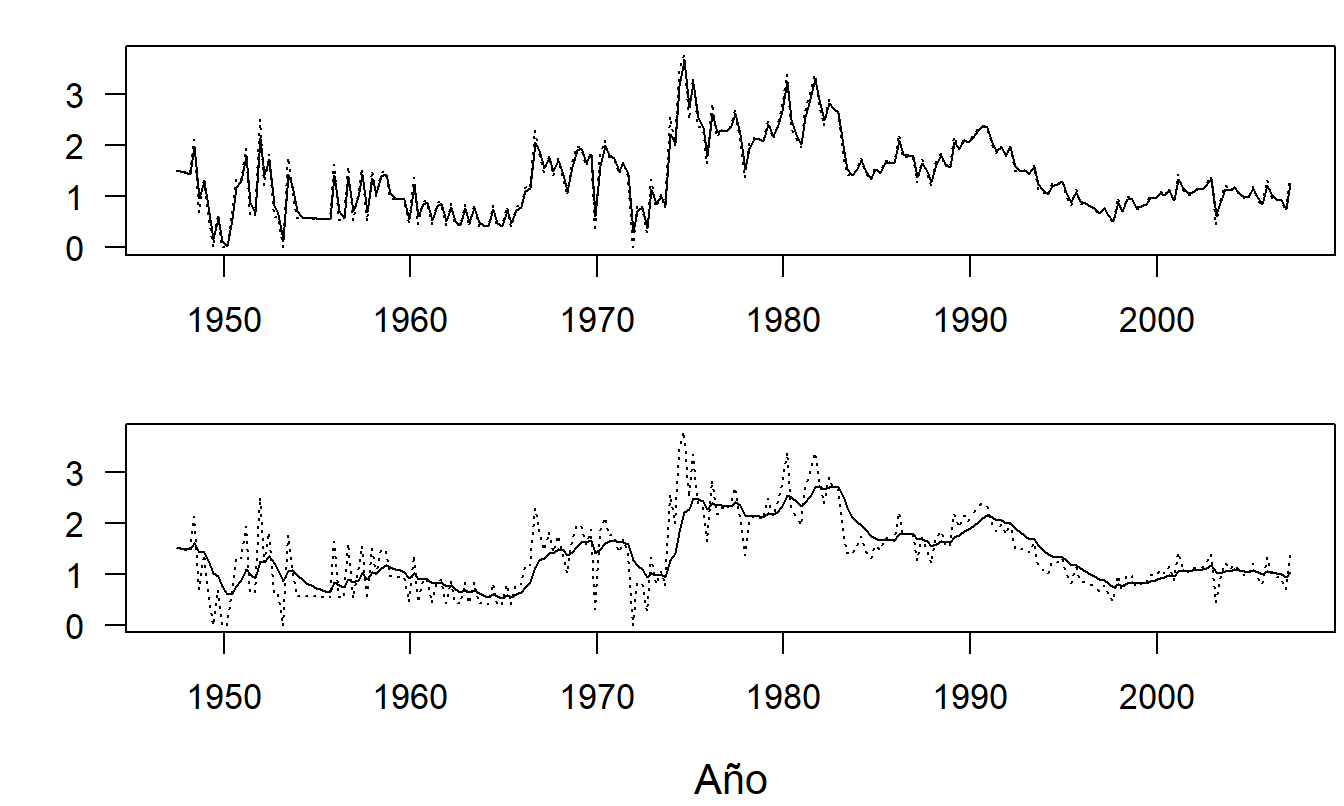
$Componente Médico del Índice de Precios al Consumidor con Suavización. En ambos paneles, la línea discontinua es el índice. En el panel superior, la línea continua es la versión suavizada con $w$=0.2. En el panel inferior, la línea continua es la versión suavizada con $w$=0.8.$

Figura 9.2: Componente Médico del Índice de Precios al Consumidor con Suavización. En ambos paneles, la línea discontinua es el índice. En el panel superior, la línea continua es la versión suavizada con $w$=0.2. En el panel inferior, la línea continua es la versión suavizada con $w$=0.8.

La ecuación (9.5) también sugiere usar la relación $\widehat{y}_{T+l} = \widehat{s}_T$ para nuestro pronóstico de $y_{T+l}$, es decir, la serie en $l$ unidades de tiempo hacia el futuro. Los pronósticos no solo proporcionan una forma de predecir el futuro, sino también de evaluar el ajuste. En el tiempo $t-1$, nuestro “pronóstico” de $y_t$ es $\widehat{s}_{t-1}$. La diferencia se llama el error de predicción de un paso.

Para evaluar el grado de ajuste, usamos la suma de los cuadrados de los errores de predicción de un paso \[\begin{equation} SS\left( w\right) = \sum_{t=1}^T \left( y_t - \widehat{s}_{t-1} \right)^2. \tag{9.6} \end{equation}\] Es importante notar que esta suma de cuadrados es una función del parámetro de suavización, $w$. Esto proporciona un criterio para elegir el parámetro de suavización: elegir el $w$ que minimice $SS\left( w\right)$. Tradicionalmente, los analistas han recomendado que $w$ se encuentre dentro del intervalo (.70, .95), sin proporcionar un criterio objetivo para la elección. Aunque minimizar $SS\left( w\right)$ proporciona un criterio objetivo, también es intensivo computacionalmente. En ausencia de una rutina numérica sofisticada, esta minimización generalmente se realiza calculando $SS\left( w\right)$ para varios valores de $w$ y eligiendo el $w$ que proporcione el valor más pequeño de $SS\left( w\right)$.

Para ilustrar la elección del parámetro de suavización exponencial $w$, volvemos al ejemplo del IPC médico. La Figura 9.3 resume el cálculo de $SS\left( w\right)$ para varios valores de $w$. Para este conjunto de datos, parece que una elección de $w \approx 0.50$ minimiza $SS(w)$.

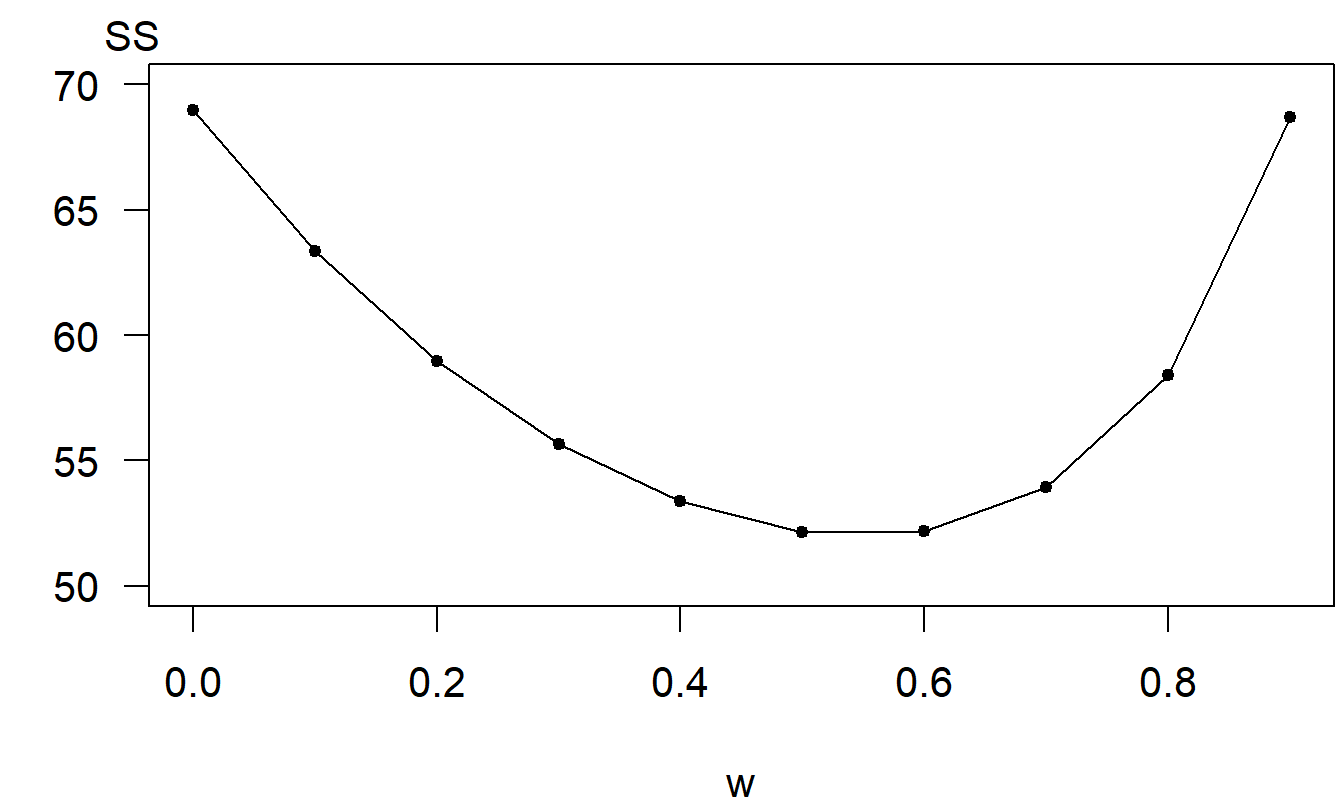
$Suma de los Cuadrados de los Errores de Predicción de un Paso. Gráfico de la suma de los cuadrados de los errores de predicción $SS(w)$ como una función del parámetro de suavización exponencial $w$.$

Figura 9.3: Suma de los Cuadrados de los Errores de Predicción de un Paso. Gráfico de la suma de los cuadrados de los errores de predicción $SS(w)$ como una función del parámetro de suavización exponencial $w$.

Al igual que con los promedios móviles, la presencia de una tendencia lineal en el tiempo, $T_t = \beta_0 + \beta_1 t$, puede manejarse mediante el siguiente procedimiento de suavización doble:

Crear una serie suavizada utilizando la ecuación (9.5), es decir, $\widehat{s}_t^{(1)} = (1-w) y_t + w \widehat{s}_{t-1}^{(1)}.$
Crear una serie suavizada doble utilizando la ecuación (9.5) y tratando la serie suavizada creada en el paso (i) como entrada. Es decir, $\widehat{s}_t^{(2)} = (1-w) \widehat{s}_t^{(1)} + w\widehat{s}_{t-1}^{(2)}$.

La estimación de la tendencia es $b_{1,T} = ((1-w)/w)(\widehat{s}_T^{(1)}- \widehat{s}_T^{(2)})$. Los pronósticos se obtienen mediante $\widehat{y}_{T+l}= b_{0,T}+b_{1,T}~l$, donde la estimación del intercepto es $b_{0,T} = 2\widehat{s}_T^{(1)} - \widehat{s}_T^{(2)}$. También mostraremos cómo usar la suavización exponencial para datos con patrones estacionales en la Sección 9.3.

Mínimos Cuadrados Ponderados

Al igual que con los promedios móviles, una característica importante de las estimaciones suavizadas exponencialmente es que pueden expresarse como estimaciones de mínimos cuadrados ponderados (WLS, por sus siglas en inglés). Para ver esto, para el modelo $y_t = \beta_0 + \varepsilon_t,$ la suma ponderada de cuadrados en la ecuación (9.3) se reduce a \[ WSS_T\left( b_0^{\ast}\right) = \sum_{t=1}^T w_t \left( y_t - b_0^{\ast} \right)^2. \] El valor de $b_0^{\ast}$ que minimiza $WSS_T\left( b_0^{\ast} \right)$ es $b_0 = \left( \sum_{t=1}^T w_t y_t \right) / \left( \sum_{t=1}^T w_t \right)$. Con la elección $w_t = w^{T-t}$, tenemos $b_0 \approx \widehat{s}_T$, donde hay igualdad excepto por el pequeño detalle del valor inicial. Por lo tanto, las estimaciones de suavización exponencial son estimaciones de $WLS$. Además, debido a la forma de los pesos elegidos, las estimaciones de suavización exponencial también se llaman estimaciones de mínimos cuadrados con descuento. Aquí, $w_t=w^{T-t}$ es una función de descuento que podría usarse al considerar el valor temporal del dinero.

9.3 Modelos de Series Temporales Estacionales

Los patrones estacionales aparecen en muchas series temporales que surgen en el estudio de los negocios y la economía. Los modelos de estacionalidad se utilizan principalmente para abordar patrones que surgen como resultado de un fenómeno físico identificable. Por ejemplo, los patrones estacionales del clima afectan la salud de las personas y, a su vez, la demanda de medicamentos recetados. Estos mismos modelos estacionales pueden utilizarse para modelar comportamientos cíclicos más prolongados.

Existen diversas técnicas disponibles para manejar patrones estacionales, incluidas los efectos estacionales fijos, los modelos autorregresivos estacionales y los métodos de suavización exponencial estacional. A continuación, abordamos cada una de estas técnicas.

Efectos Estacionales Fijos

Recuerde que, en las ecuaciones (7.1) y (7.2), usamos $S_t$ para representar los efectos estacionales bajo los modelos de descomposición aditiva y multiplicativa, respectivamente. Un modelo de efectos estacionales fijos representa $S_t$ como una función del tiempo $t$. Los dos ejemplos más importantes son las funciones estacionales binarias y las funciones trigonométricas. La Sección 7.2, Ejemplo de Tendencias en la Votación, mostró cómo usar una variable estacional binaria y el Ejemplo del Costo de los Medicamentos Recetados a continuación demostrará el uso de funciones trigonométricas. El calificativo “efectos fijos” significa que las relaciones son constantes en el tiempo. En contraste, tanto las técnicas de suavización exponencial como las autorregresivas nos proporcionan métodos que se adaptan a eventos recientes y permiten tendencias que cambian con el tiempo.

Una amplia clase de patrones estacionales puede representarse utilizando funciones trigonométricas. Considere la función \[ \mathrm{g}(t)=a\sin (ft+b) \] donde $a$ es la amplitud (el valor más alto de la curva), $f$ es la frecuencia (el número de ciclos que ocurren en el intervalo $(0,2\pi )$) y $b$ es el desplazamiento de fase. Debido a una identidad básica, $\sin (x+y) = \sin x \cos y + \sin y \cos x$, podemos escribir \[ \mathrm{g}(t) = \beta_1 \sin (ft) + \beta_2 \cos (ft) \] donde $\beta_1 = a \cos b$ y $\beta_2 = a \sin b$. Para una serie temporal con base estacional SB, podemos representar una amplia variedad de patrones estacionales utilizando \[\begin{equation} S_t = \sum_{i=1}^m a_i \sin (f_i t + b_i) = \sum_{i=1}^m \left\{ \beta_{1i} \sin (f_i t) + \beta_{2i} \cos (f_i t) \right\} \tag{9.7} \end{equation}\] con $f_i=2\pi i/SB$. Para ilustrar, la función compleja que se muestra en la Figura 9.5 fue construida como la suma de las $(m=)$ 2 funciones trigonométricas más simples que se muestran en la Figura 9.4.

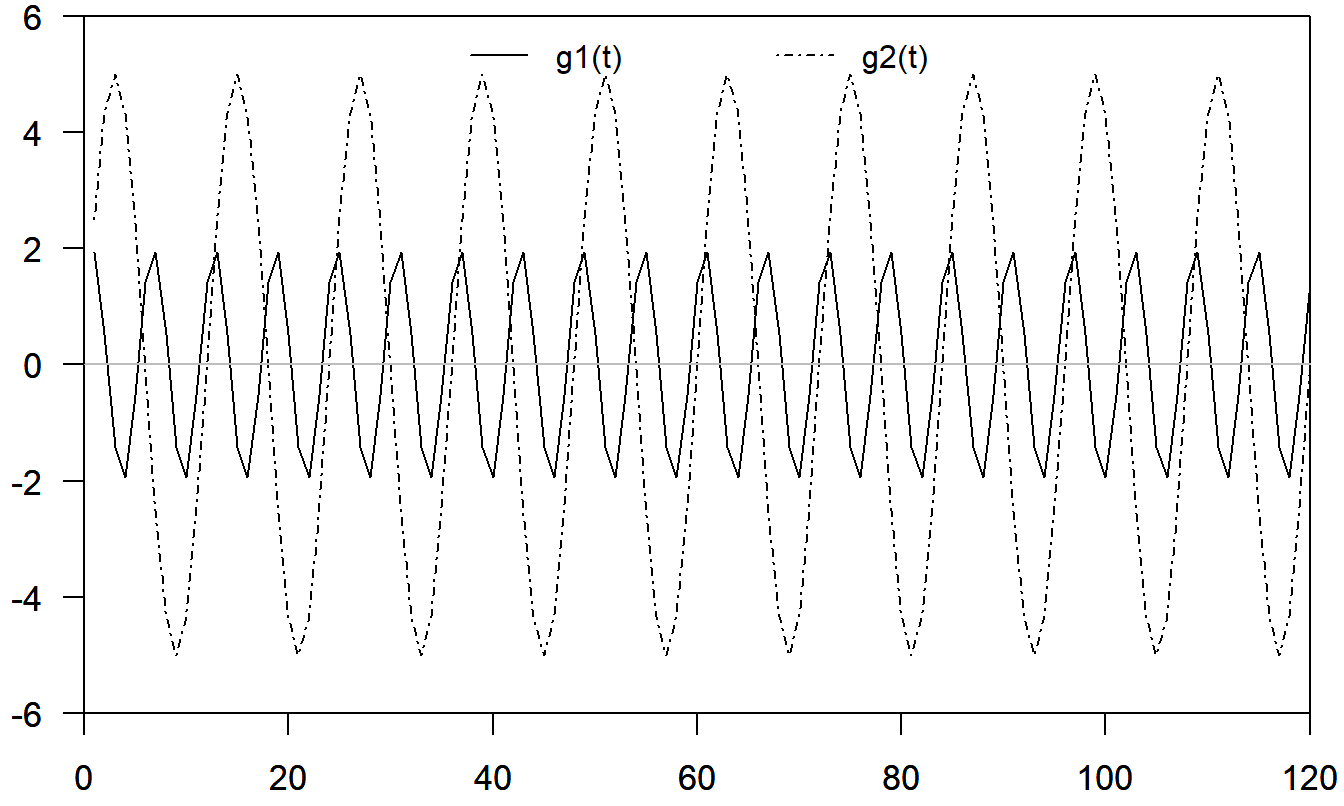
$Gráfico de Dos Funciones Trigonométricas. Aquí, g$_1(t)$ tiene amplitud $a_1=5$, frecuencia $f_1=2 \pi /12$ y desplazamiento de fase $b_1=0$. Además, g$_2(t)$ tiene amplitud $a_2=2$, frecuencia $f_2=4 \pi/12$ y desplazamiento de fase $b_2=\pi/4$.$

Figura 9.4: Gráfico de Dos Funciones Trigonométricas. Aquí, g$_1(t)$ tiene amplitud $a_1=5$, frecuencia $f_1=2 \pi /12$ y desplazamiento de fase $b_1=0$. Además, g$_2(t)$ tiene amplitud $a_2=2$, frecuencia $f_2=4 \pi/12$ y desplazamiento de fase $b_2=\pi/4$.

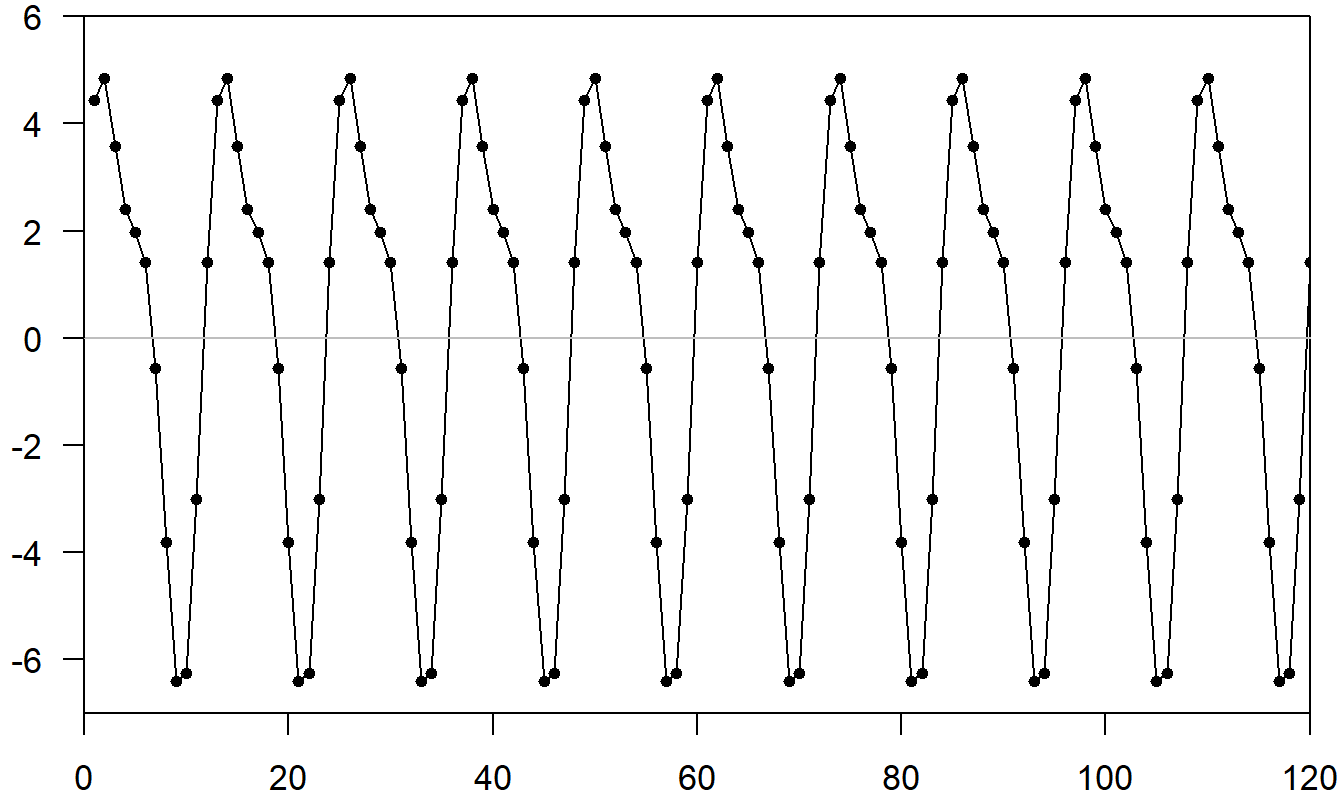
Figura 9.5: Gráfico de la Suma de Dos Funciones Trigonométricas en la Figura 9.4.

Considere el modelo $y_t=\beta_0+S_t+\varepsilon_t$, donde $S_t$ está especificado en la ecuación (9.7). Debido a que $\sin (f_it)$ y $\cos (f_it)$ son funciones del tiempo, pueden tratarse como variables explicativas conocidas. Por lo tanto, el modelo \[ y_t = \beta_0 + \sum_{i=1}^{m}\left\{ \beta_{1i}\sin (f_i t) + \beta_{2i} \cos (f_i t)\right\} + \varepsilon_t \] es un modelo de regresión lineal múltiple con $k=2m$ variables explicativas. Este modelo puede estimarse utilizando software estadístico estándar de regresión. Además, podemos usar nuestras técnicas de selección de variables para elegir $m$, el número de funciones trigonométricas. Notamos que $m$ es como máximo $SB/2$, para $SB$ par. De lo contrario, tendríamos colinealidad perfecta debido a la periodicidad de la función seno. El siguiente ejemplo demuestra cómo elegir $m$.

Ejemplo: Costo de Medicamentos Recetados. Consideramos una serie del Programa de Medicamentos Recetados del Estado de Nueva Jersey, el costo por receta. Esta serie mensual está disponible para el período de agosto de 1986 hasta marzo de 1992, inclusive.

La Figura 9.6 muestra que la serie es claramente no estacionaria, ya que el costo por receta está aumentando con el tiempo. Hay varias maneras de manejar esta tendencia. Se puede comenzar con una tendencia lineal en el tiempo e incluir reclamos de retraso para manejar autocorrelaciones. Para esta serie, un buen enfoque es considerar los cambios porcentuales en la serie de costo por receta. La Figura 9.7 es un gráfico de series temporales de los cambios porcentuales. En esta figura, vemos que muchas de las tendencias evidentes en la Figura 9.6 han sido filtradas.

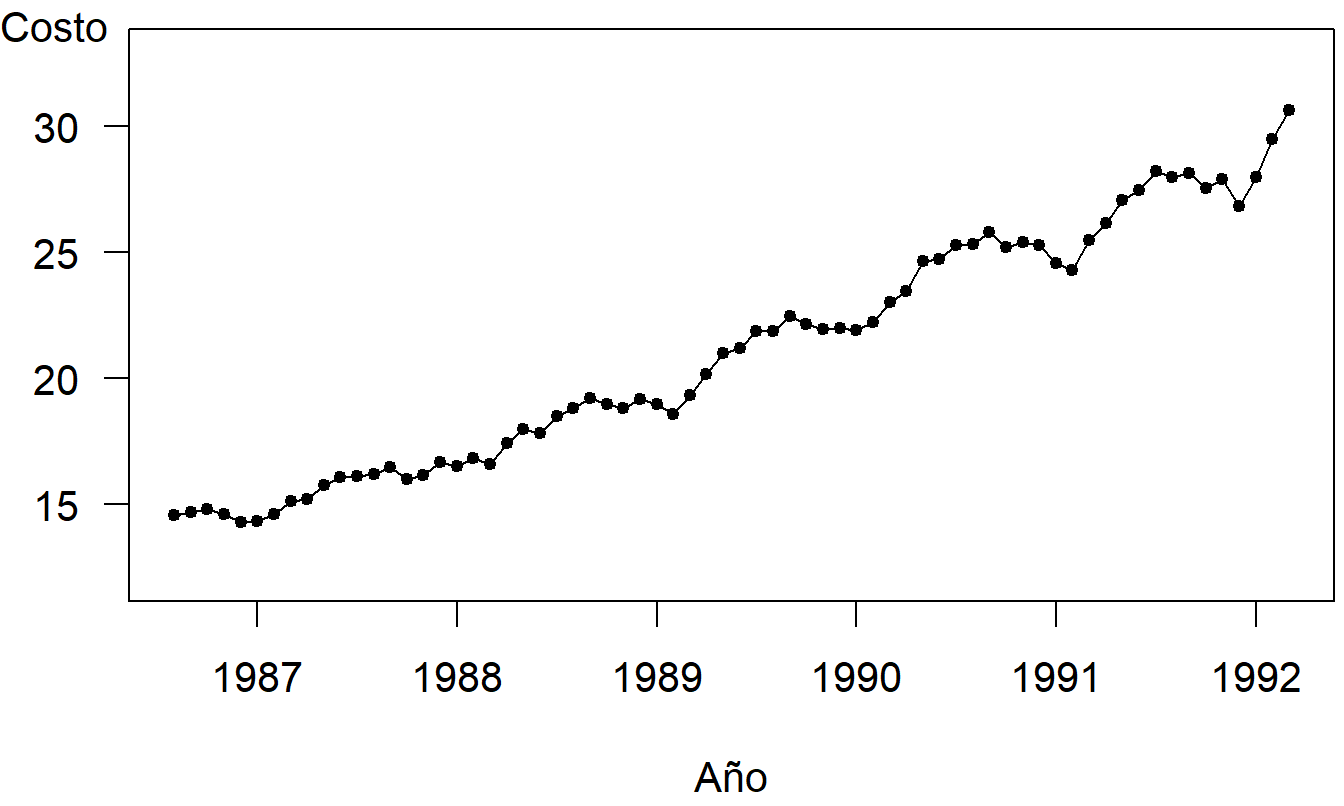
Figura 9.6: Gráfico de Series Temporales del Costo por Reclamo de Medicamentos Recetados en el Estado de Nueva Jersey.

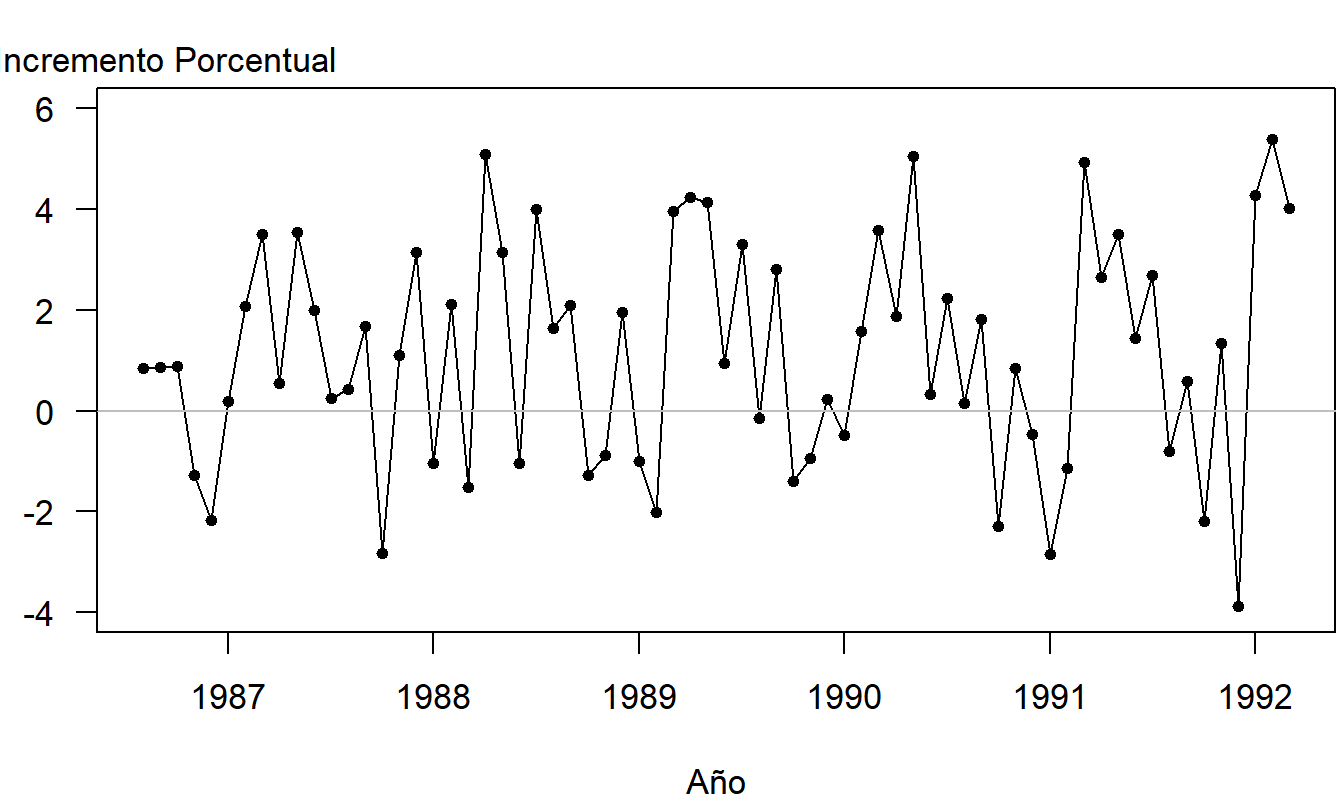
Figura 9.7: Cambios Porcentuales Mensuales del Costo por Reclamo de Medicamentos Recetados.

La Figura 9.7 muestra algunos patrones estacionales leves en los datos. Una inspección detallada de los datos revela mayores incrementos porcentuales en primavera y menores en los meses de otoño. Se ajustó una función trigonométrica usando $m=1$; el modelo ajustado es \[ \begin{array}{cccc} \widehat{y}_t= & 1.2217 & -1.6956\sin (2\pi t/12) & +0.6536\cos (2\pi t/12) \\ {\small \text{errores estándar}} & {\small (0.2325)} & {\small (0.3269)} & {\small (0.3298)} \\ {\small t-\text{estadísticos}} & {\small [5.25]} & {\small [-5.08]} & {\small [1.98]} \end{array} \]

con $s=1.897$ y $R^2=31.5$ por ciento. Este modelo revela algunos patrones estacionales importantes. Las variables explicativas son estadísticamente significativas y una prueba $F$ establece la significancia del modelo. La Figura 9.8 muestra los datos con los valores ajustados del modelo superpuestos. Estos valores ajustados superpuestos ayudan a detectar visualmente los patrones estacionales.

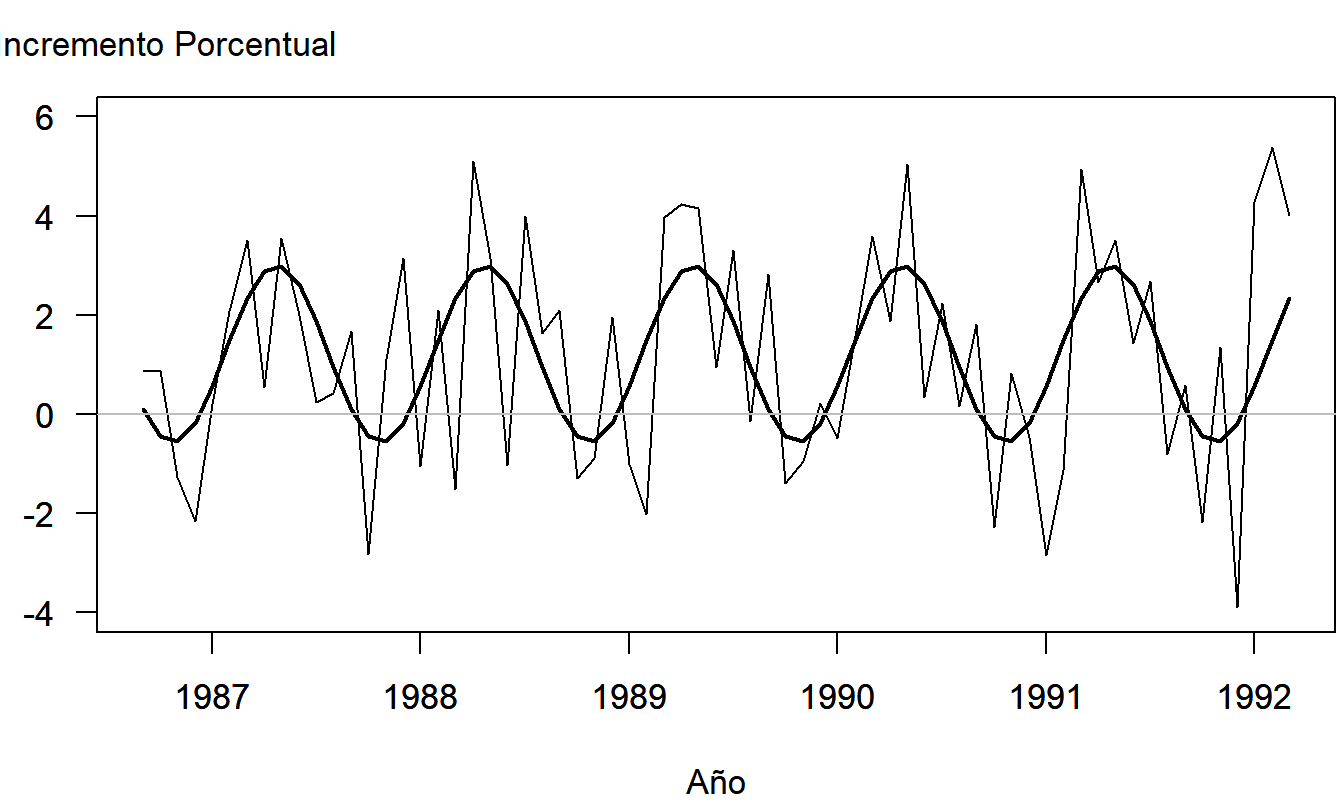
Cambios Porcentuales Mensuales del Costo por Reclamo de Medicamentos Recetados. Se han superpuesto los valores ajustados del modelo trigonométrico estacional.

Figura 9.8: Cambios Porcentuales Mensuales del Costo por Reclamo de Medicamentos Recetados. Se han superpuesto los valores ajustados del modelo trigonométrico estacional.

El examen de los residuales de este modelo ajustado reveló pocos patrones adicionales. Además, se ajustó el modelo usando $m=2$ a los datos, resultando en $R^2 = 33.6$ por ciento. Podemos decidir si usar $m=1$ o $2$ considerando el modelo \[ y_t = \beta_0 + \sum_{i=1}^2 \left\{ \beta_{1i} \sin (f_i t) + \beta_{2i} \cos (f_i t)\right\} + \varepsilon_t \] y probando $H_0:\beta_{12} = \beta_{22}=0$. Usando la prueba parcial $F$, con $n=67, k=p=2$, tenemos \[ F-ratio=\frac{(0.336-0.315)/2}{(1.000-0.336)/62} = 0.98. \] Con $df_1=p=2$ y $df_2=n-(k+p+1)=62$, el percentil 95$th$ de la distribución $F$ es $F$-value = 3.15. Debido a que $F-ratio<F-value$, no podemos rechazar $H_0$ y concluimos que $m=1$ es la opción preferida.

Finalmente, también es interesante ver cómo nuestro modelo de los datos transformados funciona con nuestros datos originales, en unidades de costo por reclamo. Los valores ajustados de los incrementos porcentuales se convirtieron de nuevo en valores ajustados de costo por reclamo. La Figura 9.9 muestra los datos originales con los valores ajustados superpuestos. Esta figura establece la fuerte relación entre las series reales y ajustadas.

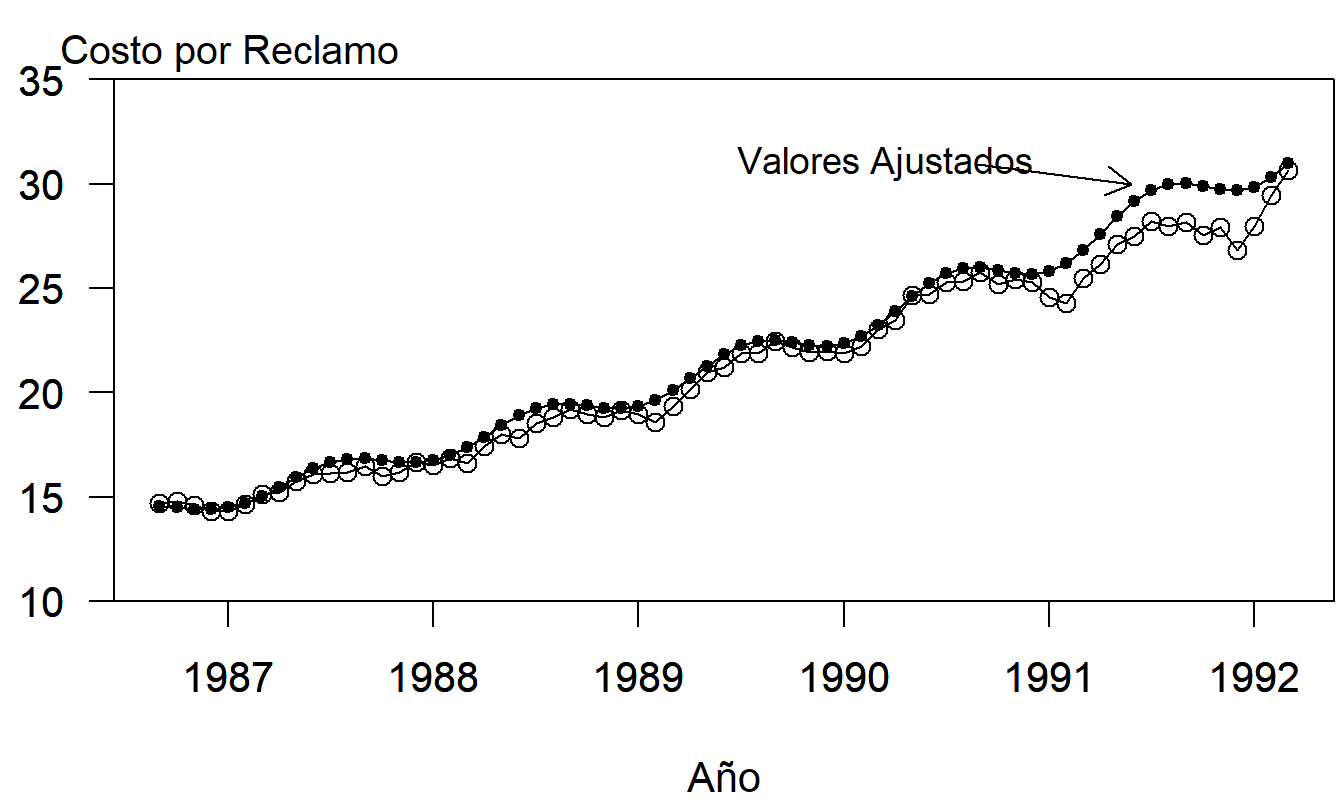
Figura 9.9: Cambios Porcentuales Mensuales del Costo por Reclamo de Medicamentos Recetados. Se han superpuesto los valores ajustados del modelo trigonométrico estacional.

Modelos Autorregresivos Estacionales

En el Capítulo 8 examinamos patrones a lo largo del tiempo utilizando las autocorrelaciones de la forma $\rho_{k}$, la correlación entre $y_t$ y $y_{t-k}$. Construimos representaciones de estos patrones temporales utilizando modelos autorregresivos, modelos de regresión con respuestas rezagadas como variables explicativas. Los patrones estacionales en el tiempo se pueden manejar de manera similar. Definimos el modelo autorregresivo estacional de orden P, SAR(P), como \[\begin{equation} y_t=\beta_0+\beta_1y_{t-SB}+\beta_2y_{t-2SB}+\ldots+\beta _{P}y_{t-PSB}+\varepsilon_t, \tag{9.8} \end{equation}\] donde $SB$ es la base estacional considerada. Por ejemplo, usando $SB=12$, un modelo estacional de orden uno, $SAR(1)$, es \[ y_t=\beta_0+\beta_1y_{t-12}+\varepsilon_t. \] A diferencia del modelo $AR(12)$ definido en el Capítulo 9, para el modelo $SAR(1)$ omitimos $y_{t-1},y_{t-2},\ldots,y_{t-11}$ como variables explicativas, aunque conservamos $y_{t-12}$.

Al igual que en el Capítulo 8, la elección del orden del modelo se realiza examinando la estructura de autocorrelación y utilizando una estrategia iterativa de ajuste del modelo. De manera similar, la elección de la estacionalidad $SB$ se basa en un examen de los datos. Remitimos al lector interesado a Abraham y Ledolter (1983).

Ejemplo: Costo de Medicamentos Recetados - Continuación. Tabla 9.1 presenta las autocorrelaciones para el incremento porcentual en el costo por reclamo de medicamentos recetados. Hay $T=67$ observaciones en este conjunto de datos, lo que resulta en un error estándar aproximado de $se(r_{k})=1/\sqrt{67}\approx 0.122$. Así, las autocorrelaciones en y alrededor de los rezagos 6, 12 y 18 parecen ser significativamente diferentes de cero. Esto sugiere usar $SB=6$. Un examen más detallado de los datos sugirió un modelo $SAR(2)$.

Table 9.1. Autocorrelaciones del Costo por Reclamos de Medicamentos Recetados

\[ \small{ \begin{array}{c|ccccccccc} \hline k & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ r_{k} & 0.08 & 0.10 & -0.12 & -0.11 & -0.32 & -0.33 & -0.29 & 0.07 & 0.08 \\ \hline k & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 \\ r_{k} & 0.25 & 0.24 & 0.31 & -0.01 & 0.14 & -0.10 & -0.08 & -0.25 & -0.18 \\ \hline \end{array} } \]

El modelo ajustado resultante es:

\[ \begin{array}{cccc} \widehat{y}_t= & 1.2191 & -0.2867y_{t-6} &+0.3120y_{t-12} \\ {\small \text{errores estándar}} & {\small (0.4064)} & {\small (0.1502)} & {\small (0.1489)} \\ {\small t-\text{estadísticos}} & {\small [3.00]} & {\small [-1.91]} & {\small [2.09]} \end{array} \]

$s=2.156$. Este modelo fue ajustado utilizando mínimos cuadrados condicionales. Note que, debido a que estamos usando $y_{t-12}$ como una variable explicativa, el primer residual que se puede estimar es el 13. Es decir, perdemos doce observaciones al realizar el rezago por doce al usar estimaciones de mínimos cuadrados.

Suavizamiento Exponencial Estacional

Un método de suavizamiento exponencial que ha gozado de considerable popularidad entre los pronosticadores es el modelo estacional aditivo de Holt-Winter. Aunque es difícil expresar los pronósticos de este modelo como estimaciones de mínimos cuadrados ponderados, el modelo parece funcionar bien en la práctica.

Holt (1957) introdujo la siguiente generalización del método de suavizamiento exponencial doble. Sea $w_1$ y $w_2$ parámetros de suavizamiento y calcule recursivamente las estimaciones de parámetros:

\[\begin{eqnarray*} b_{0,t} &=&(1-w_1)y_t+w_1(b_{0,t-1}+b_{1,t-1}) \\ b_{1,t} &=&(1-w_2)(b_{0,t}-b_{0,t-1})+w_2b_{1,t-1} . \end{eqnarray*}\] Estas estimaciones se pueden utilizar para pronosticar el modelo de tendencia lineal, $y_t = \beta_0 + \beta_1 t + \varepsilon_t$. Los pronósticos son $\widehat{y}_{T+l} = b_{0,T} + b_{1,T}~l$. Con la elección $w_1=w_2=2w/(1+w)$, se puede demostrar que el procedimiento de Holt produce las mismas estimaciones que las descritas en la Sección 9.2.

Winters (1960) extendió el procedimiento de Holt para acomodar tendencias estacionales. Específicamente, el modelo estacional aditivo de Holt-Winter es \[ y_t = \beta_0 + \beta_1 t + S_t + \varepsilon_t \] donde $S_t=S_{t-SB}, S_1+S_2+\ldots+S_{SB}=0$, y $SB$ es la base estacional. Ahora empleamos tres parámetros de suavizamiento: uno para el nivel, $w_1$, uno para la tendencia, $w_2$, y uno para la estacionalidad, $w_{3}$. Las estimaciones de los parámetros para este modelo se determinan recursivamente usando: \[\begin{eqnarray*} b_{0,t} &=&(1-w_1)\left( y_t-\widehat{S}_{t-SB}\right) +w_1(b_{0,t-1}+b_{1,t-1}) \\ b_{1,t} &=&(1-w_2)(b_{0,t}-b_{0,t-1})+w_2b_{1,t-1} \\ \widehat{S}_t &=&(1-w_{3})\left( y_t-b_{0,t}\right) +w_{3}\widehat{S} _{t-SB}. \end{eqnarray*}\] Con estas estimaciones de parámetros, los pronósticos se determinan usando: \[ \widehat{y}_{T+l}=b_{0,T}+b_{1,T}~l+\widehat{S}_T(l) \] donde $\widehat{S}_T(l)=\widehat{S}_{T+l}$ para $l=1,2,\ldots,SB$, $\widehat{S}_T(l)=\widehat{S}_{T+l-SB}$ para $l=SB+1,\ldots,2SB$, y así sucesivamente.

Para calcular las estimaciones recursivas, debemos decidir (i) valores iniciales y (ii) una elección de parámetros de suavizamiento. Para determinar valores iniciales, recomendamos ajustar una ecuación de regresión a la primera parte de los datos. La ecuación de regresión incluirá una tendencia lineal en el tiempo, $\beta_0 + \beta_1 t$, y $SB-1$ variables binarias para la variación estacional. Por lo tanto, solo se requieren $SB+1$ observaciones para determinar las estimaciones iniciales $b_{0,0}, b_{1,0}, y_{1-SB}, y_{2-SB},\ldots, y_0$.

Elegir los tres parámetros de suavizamiento es más difícil. Los analistas han encontrado complicado elegir tres parámetros utilizando un criterio objetivo, como la minimización de la suma de los errores de predicción de un paso, como en la Sección 9.2. Parte de la dificultad radica en la no linealidad de la minimización, lo que resulta en un tiempo computacional prohibitivo. Otra parte de la dificultad es que funciones como la suma de los errores de predicción de un paso a menudo resultan ser relativamente insensibles a la elección de parámetros. En cambio, los analistas han confiado en reglas prácticas para guiar la elección de los parámetros de suavizamiento. En particular, dado que los efectos estacionales pueden tardar varios años en desarrollarse, se recomienda un valor más bajo de $w_{3}$ (lo que resulta en un mayor suavizamiento). Cryer y Miller (1994) recomiendan $w_1=w_2=0.9$ y $w_{3}=0.6$.

9.4 Pruebas de Raíces Unitarias

Ahora hemos visto dos modelos en competencia que manejan la no estacionariedad con una tendencia en la media: el modelo de tendencia lineal en el tiempo y el modelo de caminata aleatoria. La Sección 7.6 ilustró cómo podemos elegir entre estos dos modelos utilizando datos fuera de la muestra. Para un procedimiento de selección basado en datos dentro de la muestra, considere el modelo \[ y_t = \mu_0 + \phi (y_{t-1} - \mu_0) + \mu_1 \left( \phi + (1-\phi) t \right) + \varepsilon_t. \] Cuando $\phi =1$, esto se reduce a un modelo de caminata aleatoria con $y_t=\mu_1+y_{t-1}+\varepsilon_t.$ Cuando $\phi <1$ y $\mu_1=0$, esto se reduce a un modelo $AR(1)$, $y_t=\beta_0+\phi y_{t-1}+\varepsilon_t$, con $\beta_0=\mu_0\left( 1-\phi \right)$. Cuando $\phi =0$, esto se reduce a un modelo de tendencia lineal en el tiempo con $y_t = \mu_0 + \mu_1 t + \varepsilon_t.$

Ejecutar un modelo donde la variable dependiente potencialmente sea una caminata aleatoria es problemático. Por lo tanto, es habitual usar mínimos cuadrados en el modelo \[\begin{equation} y_t-y_{t-1}=\beta_0+\left( \phi -1\right) y_{t-1}+\beta _1t+\varepsilon_t \tag{9.9} \end{equation}\] donde interpretamos $\beta_0=\mu_0\left( 1-\phi \right) + \phi \mu_1$ y $\beta_1=\mu_1\left( 1-\phi \right).$ A partir de esta regresión, sea $t_{DF}$ el estadístico $t$ asociado con la variable $y_{t-1}$. Deseamos usar el estadístico $t$ para probar la hipótesis nula $H_0:\phi =1$ frente a la alternativa unilateral $H_{a}:\phi <1$. Dado que $\{y_{t-1}\}$ es un proceso de caminata aleatoria bajo la hipótesis nula, la distribución de $t_{DF}$ no sigue la distribución $t$ habitual, sino una distribución especial, debida a Dickey y Fuller (1979). Esta distribución ha sido tabulada y programada en varios paquetes estadísticos, Fuller (1996).

Ejemplo: Tasas de Participación Laboral - Continuación. Ilustramos el rendimiento de las pruebas de Dickey-Fuller en las tasas de participación laboral introducidas en el Capítulo 7. Allí, establecimos que la serie era claramente no estacionaria y que los pronósticos fuera de la muestra mostraron que la caminata aleatoria era preferida en comparación con el modelo de tendencia lineal en el tiempo.

Tabla 9.2 resume la prueba. Tanto sin ($\mu_1 = 0$) como con ($\mu_1 \neq 0$) la línea de tendencia, el estadístico $t$ ($t_{DF}$) no es estadísticamente significativo (en comparación con el valor crítico del 10%). Esto proporciona evidencia de que la caminata aleatoria es la elección de modelo preferida.

Table 9.2. Estadísticos de Prueba de Dickey-Fuller con Valores Críticos

\[ \small{ \begin{array}{c|cccc} \hline & \text{Sin Tendencia} & &\text{Con Tendencia} \\ & & 10\% ~ \text{Crítico} & & 10\%~ \text{Crítico} \\ \text{Rezago} (p)& t_{DF} & \text{Valor} & t_{DF} & \text{Valor} \\ \hline & -1.614 & -2.624 & -0.266 & -3.228 \\ 1 & -1.816 & -2.625 & -0.037 & -3.230 \\ 2 & -1.736 & -2.626 & 0.421 & -3.233 \\ \hline \end{array} } \]

Una crítica a la prueba de Dickey-Fuller es que se presume que el término de perturbación en la ecuación (9.9) no tiene correlación serial. Para protegernos contra esto, una alternativa comúnmente utilizada es el estadístico de prueba de Dickey-Fuller aumentada. Este es el estadístico $t$ asociado con la variable $y_{t-1}$ utilizando mínimos cuadrados ordinarios en la siguiente ecuación: \[\begin{equation} y_t-y_{t-1}=\beta_0+\left( \phi -1\right) y_{t-1}+\beta _1t+\sum_{j=1}^{p}\phi_{j}\left( y_{t-j}-y_{t-j-1}\right) +\varepsilon_t. \tag{9.10} \end{equation}\] En esta ecuación, hemos aumentado el término de perturbación con términos autorregresivos en las diferencias {$y_{t-j}-y_{t-j-1}$}. La idea es que estos términos sirven para capturar la correlación serial en el término de perturbación. La investigación no ha llegado a un consenso sobre cómo elegir el número de rezagos ($p$); en la mayoría de las aplicaciones, los analistas proporcionan los resultados del estadístico de prueba para varias opciones de rezagos y esperan que las conclusiones alcanzadas sean cualitativamente similares. Este es ciertamente el caso para las tasas de participación laboral, como se demuestra en la Tabla 9.2. Aquí, vemos que para cada elección de rezago, no se puede rechazar la hipótesis nula de la caminata aleatoria.

9.5 Modelos ARCH/GARCH

Hasta este punto, nos hemos centrado en pronosticar el nivel de la serie, es decir, la media condicional. Sin embargo, hay aplicaciones importantes, notablemente en el estudio de las finanzas, donde es importante pronosticar la variabilidad. Para ilustrarlo, la varianza desempeña un papel clave en la valoración de opciones, como al usar la fórmula de Black-Scholes.

Muchas series temporales financieras exhiben agrupamiento de volatilidad, es decir, períodos de alta volatilidad (grandes cambios en la serie) seguidos por períodos de baja volatilidad. Para ilustrarlo, considere lo siguiente.

Ejemplo: Rendimientos diarios del S & P 500. La Figura 9.10 proporciona un gráfico de series temporales de los rendimientos diarios del Standard & Poor’s 500 durante el período 2000-2006, inclusive. Aquí, vemos que la primera parte de la serie, antes de enero de 2003, es más volátil en comparación con la última parte de la serie. Excepto por la volatilidad cambiante, la serie parece ser estacionaria, sin aumentos o disminuciones dramáticas.

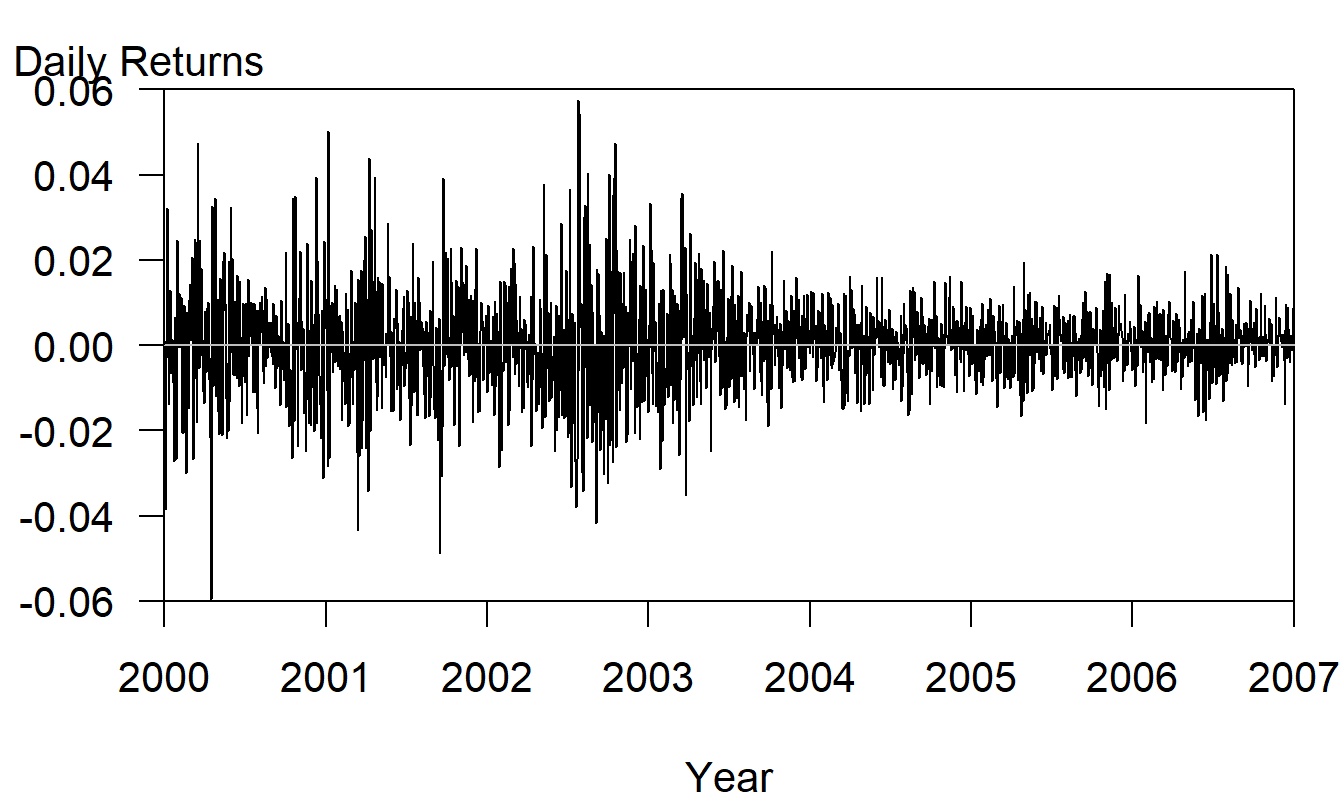
Figura 9.10: Gráfico de Series Temporales de los Rendimientos Diarios del S&P, 2000-2006, inclusive.

El concepto de variabilidad cambiante a lo largo del tiempo parece estar en conflicto con nuestras nociones de estacionariedad. Esto se debe a que una condición para la estacionariedad débil es que la serie tenga una varianza constante. Lo sorprendente es que podemos permitir varianzas cambiantes condicionando al pasado y aún así mantener un modelo débilmente estacionario. Para verlo matemáticamente, usamos la notación $\Omega_t$ para denotar el conjunto de información, la colección de conocimientos sobre el proceso hasta e incluyendo el tiempo $t$. Para una serie débilmente estacionaria, podemos denotar esto como $\Omega _t=\{\varepsilon_t,\varepsilon_{t-1},\ldots\}$. Permitimos que la varianza dependa del tiempo $t$ condicionando al pasado, \[ \sigma_t^2=\mathrm{Var}_{t-1}\left( \varepsilon_t\right) =\mathrm{E} \left( \left[ \varepsilon_t-\mathrm{E}\left( \varepsilon_t|\Omega _{t-1}\right) \right] ^2|\Omega_{t-1}\right) . \] Ahora presentamos varios modelos paramétricos de $\sigma_t^2$ que nos permiten cuantificar y pronosticar esta volatilidad cambiante.

Modelo ARCH

El modelo de heterocedasticidad cambiante autorregresiva de orden p, $ARCH(p),$ es debido a Engle (1982). Ahora asumimos que la distribución de $\varepsilon_t$ dado $\Omega_{t-1}$ es normal con media cero y varianza $\sigma_t^2$. Además, asumimos que la varianza condicional se determina recursivamente por \[ \sigma_t^2=w+\gamma_1\varepsilon_{t-1}^2+\ldots+\gamma _{p}\varepsilon_{t-p}^2=w+\gamma (B)\varepsilon_t^2, \] donde $\gamma (x)=\gamma_1x+\ldots+\gamma_{p}x^{p}.$ Aquí, $w>0$ es el parámetro de volatilidad “a largo plazo” y $ _1,,_p$ son coeficientes tales que $\gamma _j \geq 0$ y $\gamma (1)=\sum_{j=1}^{p} \gamma_j < 1$.

En el caso de que $p=1$, podemos ver que un cambio grande en la serie $\varepsilon_{t-1}^2$ puede inducir una gran varianza condicional $\sigma_t^2$. Órdenes más altos de $p$ ayudan a capturar efectos a más largo plazo. Por lo tanto, este modelo es intuitivamente atractivo para los analistas. Curiosamente, Engle proporcionó condiciones adicionales leves para asegurar que $\{\varepsilon_t\}$ sea débilmente estacionaria. Así, a pesar de tener una varianza condicional cambiante, la varianza incondicional permanece constante a lo largo del tiempo.

Modelo GARCH

El modelo GARCH generalizado de orden p, $GARCH(p,q),$ complementa al modelo $ARCH$ de la misma manera que el promedio móvil complementa al modelo autorregresivo. Al igual que el modelo $ARCH$, asumimos que la distribución de $\varepsilon_t$ dado $\Omega_{t-1}$ sigue una distribución normal con media cero y varianza $\sigma_t^2$. La varianza condicional se determina recursivamente mediante \[ \sigma_t^2-\delta_1\sigma_{t-1}^2+-\ldots-\delta_{q}\sigma _{t-q}^2=w+\gamma_1\varepsilon_{t-1}^2+\ldots+\gamma_{p}\varepsilon _{t-p}^2, \] o $\sigma_t^2=w+\gamma (B)\varepsilon_t^2+\delta (B)\sigma_t^2,$ donde $\delta (x)=\delta_1x+\ldots+\delta_{q}x^{q}.$ Además de los requisitos del modelo $ARCH(p)$, también necesitamos que $\delta_{j}\geq 0$ y $\gamma (1)+\delta \left( 1\right) <1$.

Resulta que el modelo $GARCH(p,q)$ también es débilmente estacionario, con media cero y varianza (incondicional) $\mathrm{Var~}\varepsilon_t=w/(1-\gamma (1)-\delta \left( 1\right) ).$

Ejemplo: Rendimientos Diarios del S & P 500 - Continuado. Tras un examen de los datos (detalles no presentados aquí), se ajustó un modelo $MA(2)$ a la serie con errores $GARCH(1,1)$. Específicamente, si $y_t$ denota el rendimiento diario del S & P, para $t=1,\ldots,1759$, se ajustó el modelo \[ y_t = \beta_0 + \varepsilon_t - \theta_1 \varepsilon_{t-1} - \theta_2 \varepsilon_{t-2}, \] donde la varianza condicional se determina recursivamente mediante \[ \sigma_t^2 - \delta_1 \sigma_{t-1}^2 = w + \gamma_1 \varepsilon_{t-1}^2. \]

El modelo ajustado aparece en la Tabla 9.3. Aquí, el paquete estadístico que utilizamos emplea máxima verosimilitud para determinar los parámetros estimados, así como los errores estándar necesarios para los $t$-estadísticos. Los $t$-estadísticos muestran que todas las estimaciones de los parámetros, excepto $\theta_1$, son estadísticamente significativas. Como se discutió en el Capítulo 8, la convención es retener los coeficientes de menor orden, como $\theta_1$, si los coeficientes de mayor orden, como $\theta_2$, son significativos. Observe en la Tabla 9.3 que la suma del coeficiente $ARCH$ ($\delta_1$) y el coeficiente $GARCH$ ($\gamma_1$) es casi uno, con el coeficiente $GARCH$ sustancialmente mayor que el coeficiente $ARCH$. Este fenómeno también se reporta en Diebold (2004, página 400), quien afirma que se encuentra comúnmente en estudios de rendimientos de activos financieros.

Tabla 9.3. Modelo Ajustado para Rendimientos Diarios del S & P 500

\[ \small{ \begin{array}{crr} \hline \text{Parámetro} & \text{Estimación} & t-\text{estadístico} \\ \hline \beta_0 & 0.0004616 & 2.51 \\ \theta_1 & -0.0391526 & -1.49 \\ \theta_2 & -0.0612666 & -2.51 \\ \delta_1 & 0.0667424 & 6.97 \\ \gamma_1 & 0.9288311 & 93.55 \\ w & 5.61\times 10^{-7} & 2.30 \\ \text{Log-verosimilitud} & 5,658.852 & \\ \hline \end{array} } \]

9.6 Lecturas y Referencias Adicionales

Para otras variaciones del método de promedio móvil y suavización exponencial, consulte Abraham y Ledolter (1983).

Para un tratamiento más detallado de las pruebas de raíz unitaria, remitimos al lector a Diebold (2004) o Fuller (1996) para un tratamiento más avanzado.

Referencias del Capítulo

Abraham, Bovas and Ledolter, Johannes (1983). Statistical Methods for Forecasting. John Wiley & Sons, New York.
Cryer, Jon D. and Robert B. Miller (1994). Statistics for Business: Data Analysis and Modelling. PWS-Kent, Boston.
Dickey, D. A. and Wayne A. Fuller (1979). Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74, 427-431.
Diebold, Francis X. (2004). Elements of Forecasting , Third Edition. Thomson, South-Western, Mason Ohio.
Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of UK inflation. Econometrica 50, 987-1007.
Fuller, Wayne A. (1996). Introduction to Statistical Time Series, Second Edition. John Wiley & Sons, New York.
Holt, C. C. (1957). Forecasting trends and seasonals by exponenetially weighted moving averages. O.N.R. Memorandum, No. 52, Carnegie Institute of Technology.
Winters, P. R. (1960). Forecasting sales by exponentially weighted moving averages. Management Science 6, 324-342.