Capítulo 19 Triángulos de Reclamos
Vista Previa del Capítulo. Este capítulo introduce un problema clásico de reservación actuarial que se encuentra ampliamente en los seguros de propiedad y accidentes, así como en los seguros de salud. Los datos se presentan en un formato triangular para enfatizar su naturaleza longitudinal y censurada. Este capítulo explica cómo surgen naturalmente estos datos e introduce métodos de regresión para abordar el problema de la reservación actuarial.
19.1 Introducción
En muchos tipos de seguros, poco tiempo transcurre entre el evento de un reclamo, la notificación a una compañía de seguros y el pago a los beneficiarios. Por ejemplo, en los seguros de vida, la notificación y el pago de beneficios típicamente ocurren dentro de las dos semanas posteriores al fallecimiento del asegurado. Sin embargo, en otras líneas de seguro, el tiempo desde la ocurrencia del reclamo hasta el pago final puede ser mucho más largo, tomando meses e incluso años. Para introducir esta situación, esta sección describe la evolución de un reclamo, introduce medidas de resumen utilizadas por las aseguradoras y luego describe el método determinista predominante para pronosticar reclamos, el método del eslabón en cadena.
19.1.1 Evolución de los Reclamos
Por ejemplo, suponga que usted sufre una lesión en un accidente automovilístico cubierto por un seguro. Puede tomar meses para que la lesión se cure y todos los pagos por atención médica sean conocidos y realizados por la compañía de seguros. Además, pueden surgir disputas entre usted, otras partes involucradas en el accidente, su aseguradora y las aseguradoras de otras partes, alargando así el tiempo hasta que los reclamos se resuelvan y paguen. Cuando los reclamos tardan mucho en desarrollarse, las obligaciones del reclamo de una aseguradora pueden ser incurridas en un período contable pero no pagadas hasta un período contable posterior. En el ejemplo de su accidente, la aseguradora sabe que ha ocurrido un reclamo e incluso puede haber realizado algunos pagos en el período contable actual. Las cantidades de pagos futuros son desconocidas al final del período contable actual, pero la aseguradora desea realizar un pronóstico preciso de las obligaciones futuras para apartar una cantidad adecuada de dinero para estas obligaciones futuras, conocido como una reserva. El objetivo de la aseguradora es utilizar la información actual del reclamo para predecir el momento y la cantidad de los pagos futuros del reclamo.
Para establecer la terminología, es útil seguir la línea de tiempo de un reclamo a medida que se desarrolla. En la Figura 19.1, el reclamo ocurre en el tiempo \(t_1\) y la compañía aseguradora es notificada en el tiempo \(t_3\). Puede haber un largo intervalo entre la ocurrencia y la notificación, tal que una fecha de valoración (\(t_2\)) puede ocurrir dentro de este intervalo. Aquí, \(t_2\) es el momento en que se valoran las obligaciones, que típicamente, pero no siempre, coincide con el final de un período de reporte financiero de la compañía. En este caso, se dice que el reclamo está incurrido pero no reportado en esta fecha de valoración.
Después de la notificación del reclamo, puede haber uno o más pagos por pérdidas. No todos los pagos pueden realizarse antes de la siguiente fecha de valoración (\(t_4\)). A medida que el reclamo se desarrolla, eventualmente la compañía considera que sus obligaciones financieras sobre el reclamo están resueltas y declara el reclamo como “cerrado.” Sin embargo, es posible que surjan nuevos hechos y el reclamo deba reabrirse, dando lugar a pagos adicionales por pérdidas antes de cerrarse nuevamente.
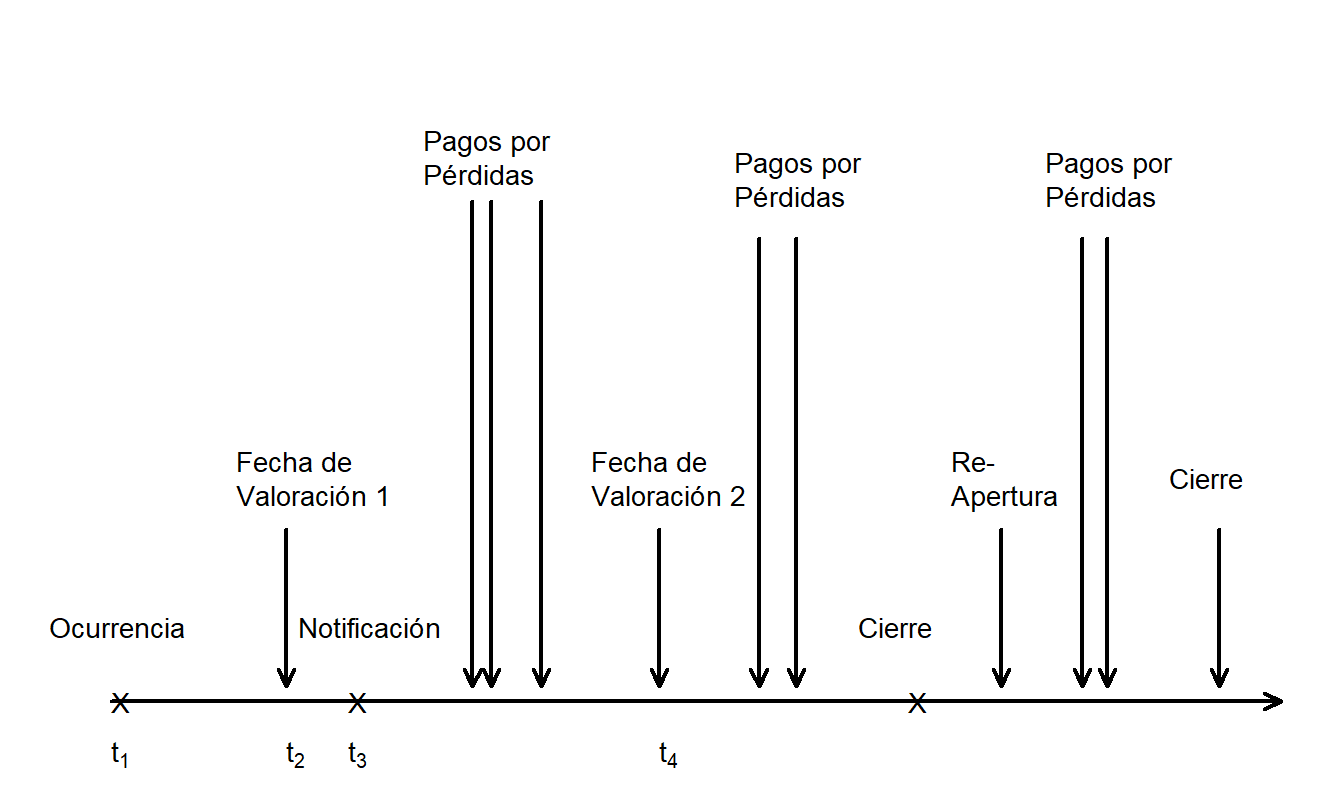
Figura 19.1: Cronología del Desarrollo de un Reclamo.
19.1.2 Triángulos de Reclamos
Las aseguradoras no suelen modelar la evolución de cada reclamo y luego sumarlos (como se hace en un análisis basado en pólizas en los seguros de vida). En cambio, los portafolios de reclamos se resumen en cada fecha de valoración; son estos resúmenes los que se utilizan para realizar pronósticos de los reclamos pendientes.
Específicamente, sea \(i\) el año en que se ha incurrido un reclamo y \(j\) el número de años desde el incurrimiento hasta el momento en que se realiza el pago, conocido como año de “desarrollo” (o “retraso”). Por lo tanto, \(y_{ij}\) representa la suma de los montos de pago en el \(i\)-ésimo año de incurrimiento y el \(j\)-ésimo año de desarrollo. Aquí, “año” se refiere al período contable; en ejemplos posteriores, verá que a menudo usamos mes, trimestre u otros períodos fijos. Tabla 19.1 muestra la información que típicamente enfrentan los actuarios.
Table 19.1. Triángulo Clásico de Desarrollo de Reclamos
\[ \small{ \begin{array}{c|ccccc} \hline \text{Año de } & \text{Año de Desarrollo }&(j) \\ \text{Incurrencia }(i) & 1& 2& 3&4&5 \\ \hline 1 & y_{11} & y_{12} & y_{13} & y_{14} & y_{15} \\ 2 & y_{21} & y_{22} & y_{23} & y_{24} & . \\ 3 & y_{31} & y_{32} & y_{33} & . & . \\ 4 & y_{41} & y_{42} & . &. & . \\ 5 & y_{51} & . & . &. & . \\ \hline \end{array} } \]
El término “triángulo de reclamos” es evidente a partir de Table 19.1. Observamos datos en el triángulo superior izquierdo, \(y_{ij}, i=1,\ldots, 5, j=1, \ldots,6-i\). El objetivo es “completar el triángulo,” es decir, pronosticar valores en el triángulo inferior derecho (\(y_{ij}, i=2,\ldots, 5, j=7-i, \ldots,5\)). Por ejemplo, el año más reciente de incurrencia es \(i=5\), para el cual solo tenemos un año de experiencia de reclamos, \(y_{51}\). Los otros valores, \(y_{5j}, j=2, \ldots,5\), son desconocidos en la fecha de valoración. En algunas situaciones, también es de interés pronosticar reclamos en años de desarrollo seis y posteriores.
Table 19.1 resalta el hecho de que los datos son tanto longitudinales como censurados. Este es el punto clave con respecto a los supuestos de modelado estadístico. En las aplicaciones, las observaciones pueden variar significativamente dependiendo del tipo y propósito. Cada elemento del triángulo puede representar pagos reales realizados por la compañía de seguros, conocidos como “pagos incrementales,” o la suma “acumulativa” de pagos desde el desarrollo. Para algunas líneas de negocio, están disponibles estimaciones de los pagos pendientes en una base reclamo por reclamo, conocidas como “estimaciones de caso.” Aquí, los elementos del triángulo pueden representar reclamos incurridos en lugar de reclamos pagados. Es decir, un reclamo incurrido es el monto pagado más la reserva. Debido a que las estimaciones de caso se revisan a medida que se recibe nueva información sobre un reclamo, no es raro que los pagos incurridos sean negativos. Además, incluso los pagos incrementales realizados pueden ser negativos debido a la reaseguradora o la recuperación de montos de reclamos por parte de otras partes responsables. (Muchas aseguradoras emiten cheques para pagar a los reclamantes rápidamente tras la ocurrencia de un accidente y luego son reembolsadas por otra parte responsable del accidente). Los datos de triángulos de reclamos también pueden estar en forma de número de notificaciones de reclamos. Este tipo de datos es particularmente útil para estimar reservas “incurridas pero no reportadas.”
Ejemplo: Daños a Propiedades en Singapur. Table 19.2 reporta pagos incrementales de un portafolio de pólizas de automóviles de una aseguradora general (de propiedad y accidentes) en Singapur. Aquí, los pagos son por daños a terceros en propiedad de pólizas de seguros de autos de cobertura total. Todos los pagos han sido ajustados usando un índice de precios al consumidor de Singapur, por lo que están en dólares constantes. Los datos corresponden a pólizas con coberturas desde 1997 hasta 2001, inclusive. Table 19.2 también proporciona las primas de estas pólizas (en miles de dólares singapurenses) para proporcionar una idea de la creciente exposición de la aseguradora a posibles obligaciones de reclamos.
Table 19.2. Pagos Incrementales en Singapur
\[ \small{ \begin{array}{lr|rrrrr} \hline \text{Año de } & \text{Prima} &\text{ Año de Desarrollo} \\ \text{Incurrencia} & \text{(en miles)} & 1 & 2 & 3 & 4 & 5 \\ \hline 1997 & 32,691 & 1,188,675 & 2,257,909 & 695,237 & 166,812 & 92,129 \\ 1998 & 33,425 & 1,235,402 & 3,250,013 & 649,928 & 211,344 & . \\ 1999 & 34,849 & 2,209,850 & 3,718,695 & 818,367 & . & . \\ 2000 & 37,011 & 2,662,546 & 3,487,034 & . & . & . \\ 2001 & 40,152 & 2,457,265 & . & . & . & . \\ \hline \end{array} } \]
Código R para Producir Tabla 19.2
19.1.3 Método de Escalera de Cadenas
Para introducir el método básico de escalera de cadenas, continuamos trabajando en el contexto del ejemplo de daños a propiedades en Singapur. Table 19.3 muestra los mismos pagos que Table 19.2 pero en forma acumulativa en lugar de incremental. Sea \(S_{ij} = y_{i1} + \cdots + y_{ij}\) denotar los reclamos acumulativos.
Table 19.3. Pagos Acumulativos en Singapur con Estimaciones de Escalera de Cadenas
\[ \scriptsize{ \begin{array}{llrrrrr|r|c} \hline \hline &&&&&&&&\text{Pérdida}\\ &&&&&&&& \text{Final} \\ \text{Año de} &&\text{Año de}& \text{Desarrollo} & &&&&\text{Relación} \\ \text{Incurrencia} & \text{Prima} &~~~~~~~~1 & 2~~~ & 3~~~& 4~~~& 5~~~& \text{Reserva} & (\%) \\ \hline 1997 & 32,691 & 1,188,675 & 3,446,584 & 4,141,821 & 4,308,633 & 4,400,762 & & 13.5 \\ 1998 & 33,425 & 1,235,402 & 4,485,415 & 5,135,343 & 5,346,687 & {\bf 5,461,012} & 114,325 & 16.3 \\ 1999 & 34,849 & 2,209,850 & 5,928,544 & 6,746,912 & {\bf 7,021,930} & {\bf 7,172,075} & 425,163 & 20.6 \\ 2000 & 37,011 & 2,662,546 & 6,149,580 & {\bf 7,109,486} & {\bf 7,399,283} & {\bf 7,557,497} & 1,407,917 & 20.4 \\ 2001 & 40,152 & 2,457,265 &{\bf 6,738,898} & {\bf 7,790,792} & {\bf 8,108,361} & {\bf 8,281,737} & 5,824,471 & 20.6 \\ \hline \text{Total} &\text{Reserva} & & & & &&7,771,877 \\ Escalera & de Cadenas& Factores & 2.742 & 1.156 & 1.041 & 1.021 & \\ \hline \hline \end{array} } \]
La relación de escalera de cadenas para el \(j\)-ésimo año de desarrollo se calcula tomando el cociente de la suma de los reclamos sobre todos los años de incurrencia para el \(j\)-ésimo año de desarrollo, dividido por la suma de los mismos pagos del año de incurrencia para el \(j-1^{er}\) año de desarrollo. Utilizando notación, tenemos: \[ CL_j = \frac {\sum_{i=1}^{6-j} S_{ij}}{\sum_{i=1}^{6-j} S_{i,j-1}}. \] Por ejemplo, \(CL_5 = 4,400,762/4,308,633 = 1.021\) y \(CL_4 = (5,346,687+4,308,633)/(5,135,343+4,141,821)= 1.041\).
Los números en negrita son pronósticos calculados recursivamente utilizando las relaciones de escalera de cadenas y \(\widehat{S}_{i,j} = CL_{j} \times \widehat{S}_{i,j-1}.\) La recursión comienza cuando se conoce el valor del pago acumulativo, de modo que \(\widehat{S}_{ij}=S_{ij}\). Por ejemplo, para el año de incurrencia 2, \(\widehat{S}_{25} = CL_5 \times S_{24} = (1.021)(5,346,687)=5,461,012\). Para el año de incurrencia 3, \(\widehat{S}_{34} = CL_4 \times S_{33} = (1.041)(6,746,912)=7,021,930\) y \(\widehat{S}_{35} = CL_5 \times \widehat{S}_{34} = (1.021)(7,021,930)=7,172,075\). Alternativamente, se puede ir directamente al último año de desarrollo y utilizar \(\widehat{S}_{35} = CL_5 \times CL_4 \times S_{33} = (1.041)(1.021)(6,746,912)=7,172,075.\)
En Tabla 19.3, la reserva es la cantidad final pronosticada menos el reclamo acumulativo pagado más reciente. La relación de pérdida final es la proporción del pronóstico de los reclamos acumulativos en el último año de desarrollo (5) respecto a las primas pagadas (expresadas como un porcentaje, recordando que las primas están en miles).
19.2 Regresión Usando Funciones del Tiempo como Variables Explicativas
El método de escalera de cadenas es una herramienta importante que los actuarios utilizan ampliamente al pronosticar reclamos. Generalmente se presenta de manera determinista, como en la Sección 19.1.3. Los modelos estocásticos alternativos para el pronóstico de reclamos tienen dos ventajas principales:
- Al modelar explícitamente la distribución de los reclamos, se pueden realizar estimaciones de la incertidumbre de los pronósticos de reserva.
- Existen muchas variaciones de las técnicas de escalera de cadenas porque se aplican en diferentes situaciones. Como vimos en el Capítulo 5, los métodos estocásticos ofrecen una forma disciplinada de selección de modelos que puede ayudar a determinar el modelo más adecuado para un conjunto de datos dado.
Como veremos, no es necesario elegir entre usar el método de escalera de cadenas y un modelo estocástico. La Sección 19.2.3 modelo Poisson sobredisperso y la Sección 19.3.1 modelo Mack generan pronósticos puntuales que son iguales a los de escalera de cadenas.
19.2.1 Modelo Lognormal
Nuestro punto de partida es el modelo lognormal para los reclamos incrementales. Es decir, consideramos un modelo de dos factores de la forma:
\[\begin{equation} \ln y_{ij} = \mu + \alpha_i + \tau_j + \varepsilon_{ij}, \tag{19.1} \end{equation}\] donde \(\{ \alpha_i \}\) son parámetros para el factor del año de incurrencia y \(\{ \tau_j \}\) son parámetros para el factor del año de desarrollo. Un modelo de regresión con dos factores se introdujo en la Sección 4.4. Recordemos que requerimos restricciones en los parámetros de los factores para su estimabilidad, como \(\sum_i \alpha_i = 0\) y \(\sum_j \tau_j= 0\). Asumiendo normalidad de \(\{\varepsilon_{ij} \}\) se deriva la especificación lognormal para los reclamos incrementales \(y_{ij}\).
Ejemplo: Lesiones a Terceros en Singapur. Tabla 19.4 reporta pagos de un portafolio de pólizas de automóviles para una aseguradora general (de bienes y accidentes) en Singapur. Los pagos, ajustados por inflación, corresponden a lesiones a terceros de pólizas de seguro integral. Los datos son para pólizas con coberturas desde 1993 hasta 2001, inclusive.
En el seguro de automóviles, generalmente se tarda más en resolver y pagar las lesiones en comparación con los reclamos por daños a la propiedad. Por lo tanto, el número de años de desarrollo, “el desgaste”, es más largo en Tabla 19.4 que en Tabla 19.2. Tabla 19.4 también muestra una falta de estabilidad en los pagos por lesiones que la Figura 19.2 nos ayuda a visualizar. El panel izquierdo muestra líneas de tendencia por desarrollo para cada año de incurrencia. El panel derecho presenta diagramas de caja de pagos logarítmicos para cada año de desarrollo. Este gráfico muestra que los pagos tienden a aumentar en los dos primeros periodos de desarrollo (\(j=1,2\)), alcanzan un pico en el tercer periodo (\(j=3\)) y luego disminuyen.
Tabla 19.4. Pagos Incrementales por Lesiones en Singapur, 1993-2001
\[ \small{ \begin{array}{c|rrrrrrrrr} \hline \text{Año de }&\text{Año de} & \text{Desarrollo} \\ \text{Incurrencia} & 1 & 2 &3 &4 & 5 & 6 & 7 & 8 & 9 \\ \hline 1993 & 14,695 & 205,515 & 118,686 & 416,286 & 93,544 & 185,043 & 37,750 & 0 &14,086 \\ 1994 & 153,615 & 467,722 & 645,513 & 421,896 & 146,576 & 96,470 & 27,765 &38,017 & . \\ 1995 & 24,741 & 547,862 & 754,475 & 417,573 & 156,596 & 55,155 & 36,984 & . & . \\ 1996 & 68,630 & 188,627 & 492,306 & 179,249 & 34,062 & 443,436 & . & . & . \\ 1997 & 29,177 & 364,672 & 437,507 & 385,571 & 529,319 & . & . & . & . \\ 1998 & 40,430 & 241,809 & 678,541 & 528,026 & . & . & . & . & . \\ 1999 & 45,125 & 372,935 & 704,168 & . & . & . & . & . & . \\ 2000 & 21,695 & 158,005 & . & . & . & . & . & . & . \\ 2001 & 6,626 & . & . & . & . & . & . & . & . \\ \hline \hline \end{array} } \]
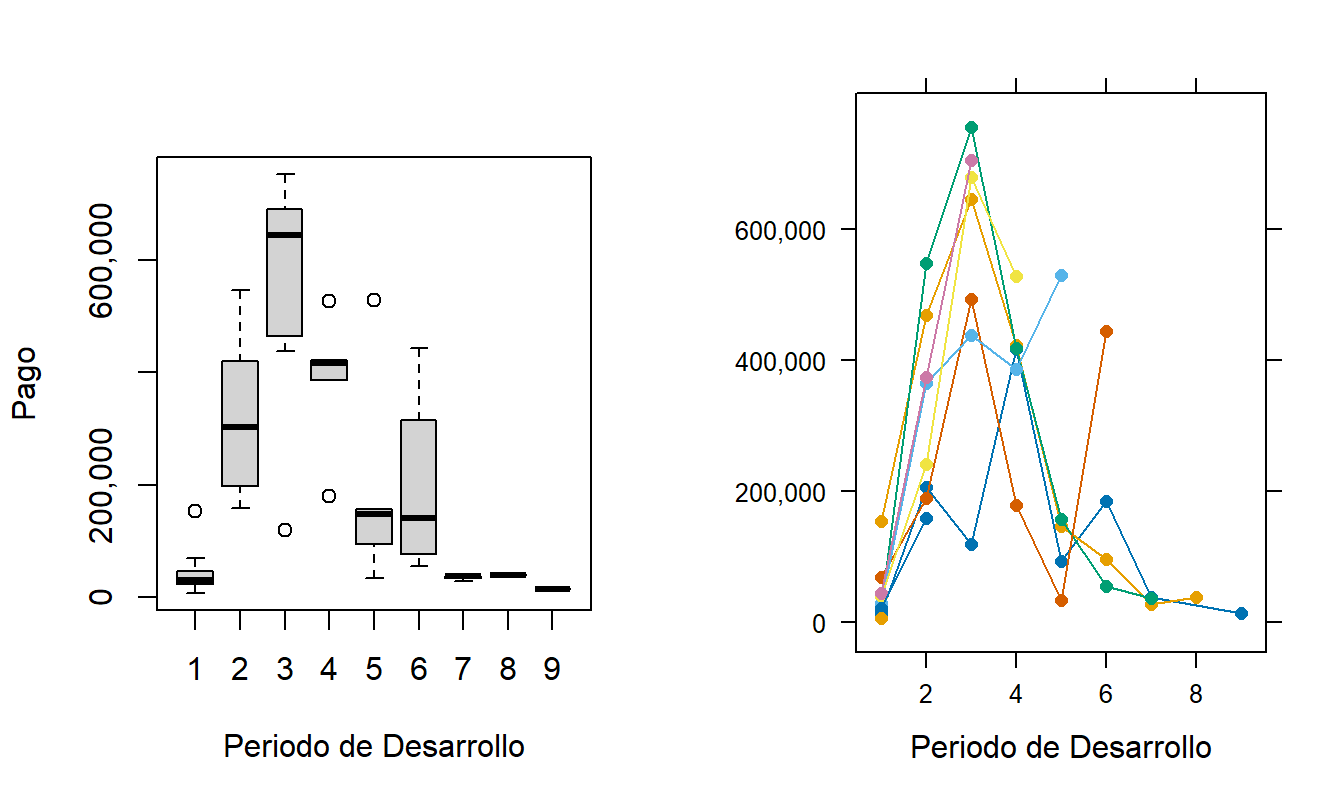
Figura 19.2: Pagos Incrementales por Lesiones en Singapur. El panel izquierdo muestra pagos por año de desarrollo con cada línea conectando pagos del mismo año de incurrencia. El panel derecho muestra la distribución de los pagos logarítmicos para cada año de desarrollo.
Código R para Producir Figura 19.2
El modelo lognormal basado en la ecuación (19.1) se ajustó a estos datos. Como era de esperar, tanto los factores de incurrencia como los años de desarrollo fueron estadísticamente significativos. El coeficiente de determinación del ajuste es \(R^2 = 73.3 \%\). Un gráfico \(qq\) (no presentado aquí) mostró una concordancia razonable con la suposición de normalidad. Los valores ajustados del modelo, después de la exponenciación para convertir de nuevo a dólares, aparecen en la Figura 19.3. Esta figura parece capturar los patrones de pago que aparecen en el panel izquierdo de la Figura 19.2. Cabe destacar que los valores ajustados para la porción no observada del triángulo son pronósticos.
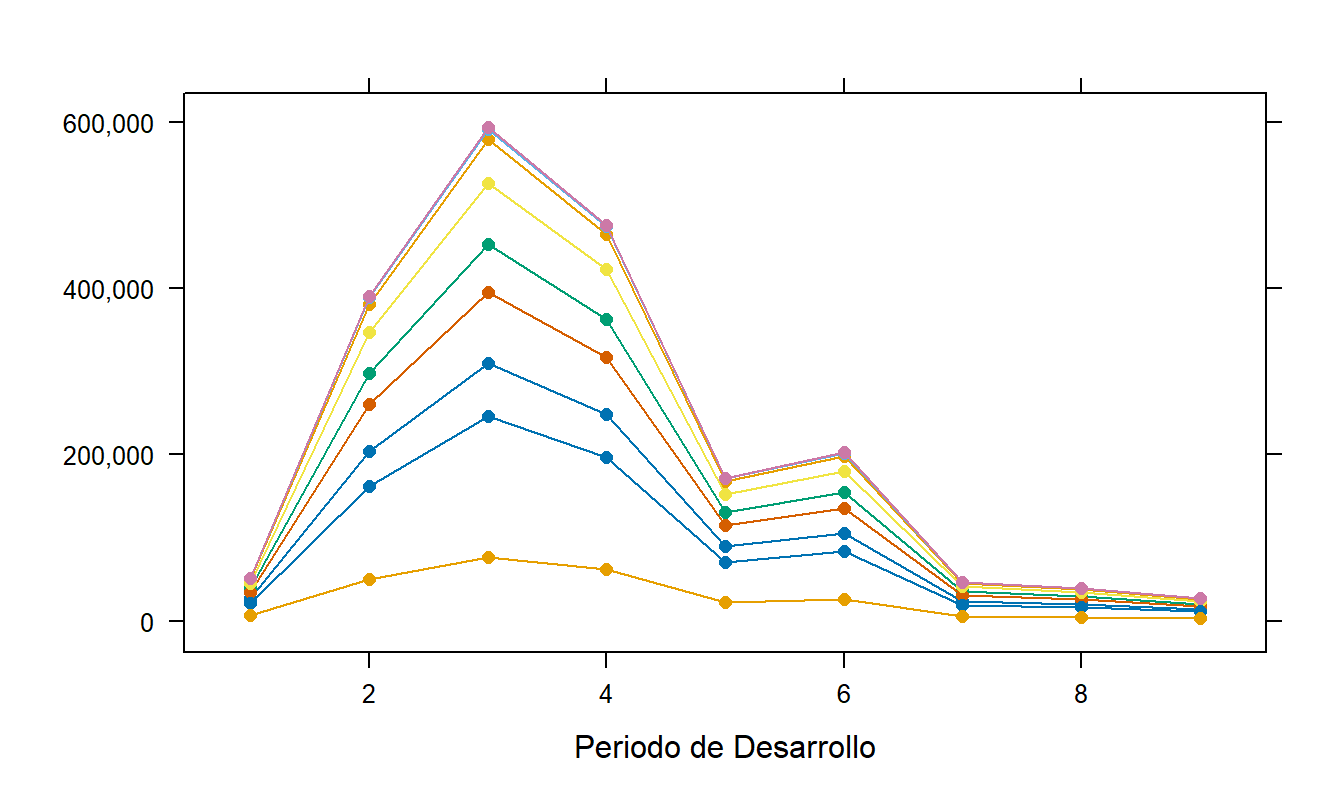
Figura 19.3: Valores Ajustados para los Pagos Incrementales por Lesiones en Singapur. Estas estimaciones están basadas en el modelo lognormal de dos factores.
Código R para Producir la Figura 19.3
19.2.2 Curva de Hoerl
La componente sistemática de la ecuación (19.1) puede ser modificada fácilmente. Una posibilidad es la denominada “curva de Hoerl,” lo que lleva a la ecuación del modelo
\[\begin{equation} \ln y_{ij} = \mu + \alpha_i + \beta_i \ln (j) + \gamma_i \times j + \varepsilon_{ij} . \tag{19.2} \end{equation}\] Una ventaja de tratar el tiempo de desarrollo \(j\) como una covariable continua es que la extrapolación es posible más allá del rango de los tiempos de desarrollo observados. Como una variación, England y Verrall (2002) sugieren permitir que los primeros años de desarrollo tengan sus propios niveles e imponer el mismo patrón de agotamiento para todos los años de incurrencia (\(\beta_i = \beta\), \(\gamma_i = \gamma\)).
Ejemplo: Lesiones de Terceros en Singapur - Continuación. El modelo básico de la ecuación (19.2) se ajustó bien, con un coeficiente de determinación de \(R^2 = 87.8 \%\). También examinamos un modelo más simple basado en la ecuación \[\begin{equation} \ln y_{ij} = \mu + \alpha_i + \beta \ln (j) + \gamma \times j + \varepsilon_{ij} . \tag{19.3} \end{equation}\] Este modelo más simple no se ajustó tan bien como el modelo más completo de Hoerl de la ecuación (19.2), teniendo \(R^2 = 78.6 \%\). Sin embargo, una prueba parcial \(F\) estableció que los parámetros adicionales no eran estadísticamente significativos, por lo que se prefirió el modelo más simple de la ecuación (19.3).
Basándonos en el modelo más simple, los valores ajustados se muestran en la Figura 19.4. Esta figura muestra los valores ajustados que disminuyen geométricamente comenzando en el cuarto período de desarrollo.
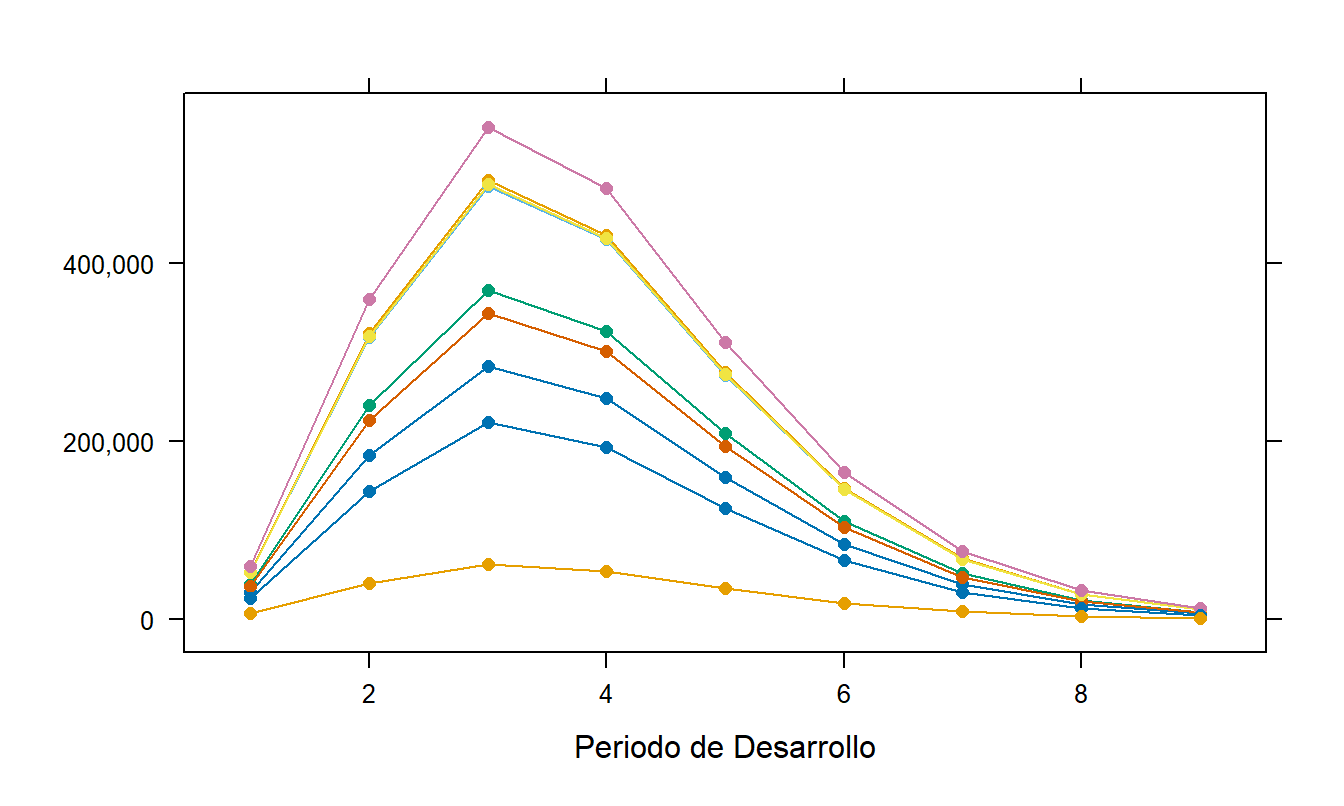
Figura 19.4: Valores Ajustados del Modelo Reducido de Hoerl en la Ecuación (19.3).
Código R para Producir la Figura 19.4
19.2.3 Modelos de Poisson
Una desventaja del modelo lognormal es que las predicciones producidas por este no replican las estimaciones tradicionales de escalera en cadena. Esta sección introduce el modelo de Poisson sobredisperso, que sí tiene esta característica deseable.
Para comenzar, a partir de la ecuación (19.1), podemos escribir \[ \mathrm{E}~ y_{ij} = \exp(\eta_{i,j})~~ \mathrm{E}~ e^{\varepsilon} \] donde el componente sistemático es \(\eta_{i,j} = \mu + \alpha_i + \tau_j\). Este es un modelo con una función de enlace logarítmica (es decir, \(\ln \mathrm{E}~y = \eta\)). En lugar de usar la distribución lognormal para \(y\), esta sección asume que \(y\) sigue un modelo de Poisson sobredisperso con función de varianza \[ \mathrm{Var}~ y_{ij} = \phi \exp(\eta_{i,j}). \] Note que hemos absorbido el escalar \(\mathrm{E}~ e^{\varepsilon}\) en el parámetro de sobredispersión \(\phi\).
Introducimos modelos de Poisson sobredispersos en la Sección 12.3. Por lo tanto, este modelo se puede estimar con software estadístico estándar y, al igual que con el modelo lognormal, se pueden producir fácilmente pronósticos. Se puede demostrar que los pronósticos producidos por el modelo de Poisson sobredisperso son equivalentes a los pronósticos determinísticos de escalera en cadena. Ver, por ejemplo, Taylor (2000) o Wüthrich y Merz (2008) para una prueba. Esto no solo nos da un mecanismo para cuantificar la incertidumbre asociada con los pronósticos de escalera en cadena, sino que también podemos usar software estadístico estándar para calcular estas estimaciones.
Ejemplo: Lesiones de Terceros en Singapur - Continuación. El modelo de Poisson sobredisperso se ajustó a los datos de pagos por lesiones en Singapur. Se utilizó software estadístico estándar para calcular las estimaciones de parámetros, utilizando las técnicas descritas en la Sección 12.3. La Figura 19.5 resume los pronósticos de estos modelos. Esta figura muestra pagos acumulativos, no incrementales, marcados con símbolos de trazado opacos en la figura. Los pronósticos de pagos incrementales se produjeron y luego se sumaron para obtener los pronósticos de pagos acumulativos en la Figura 19.5; estos están marcados con los símbolos de trazado abiertos. Se invita al lector a verificar que estos pronósticos son idénticos a los producidos por el método determinístico de escalera en cadena hasta el octavo año de desarrollo. Aquí, el valor de cero para el primer año de incurrencia causa pequeñas diferencias entre los pronósticos del modelo de Poisson y la escalera en cadena.
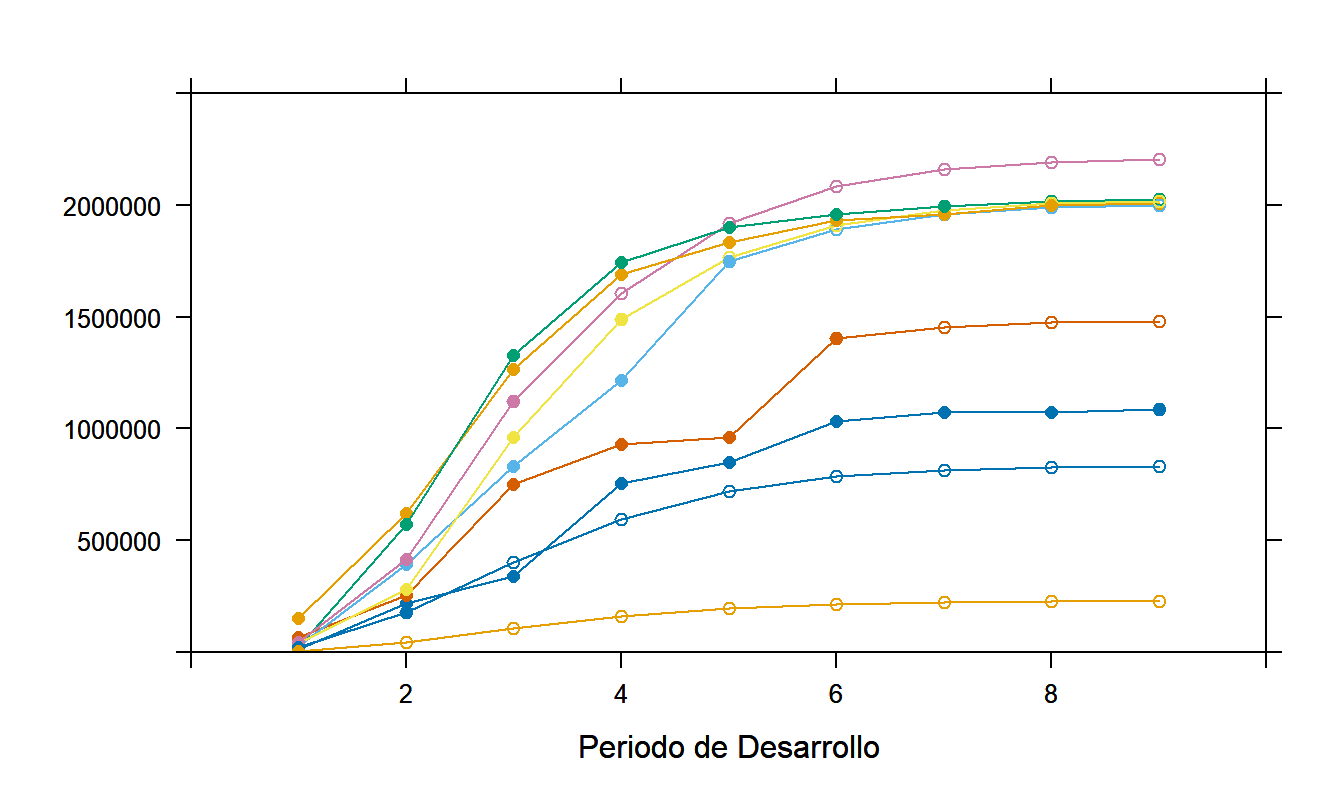
Figura 19.5: Valores Reales y Pronósticos para los Pagos Acumulativos por Lesiones en Singapur. Los valores reales están marcados con un símbolo opaco. Los pronósticos de escalera en cadena, de un modelo de Poisson sobredisperso, están marcados con un símbolo abierto.
Código R para Producir la Figura 19.5
19.3 Usando Desarrollos Pasados
Al igual que con los modelos autorregresivos, se puede usar el historial previo para pronosticar pagos. ¿Qué es el historial previo? En el marco del triángulo de reclamaciones en Tabla 19.1, hay dos dimensiones de tiempo: año de incurrencia y año de desarrollo. La mayoría de los modelos se centran en usar el desarrollo previo (“\(j\)”) para realizar pronósticos. Al centrarnos en la experiencia de desarrollo previo, nos permitimos la flexibilidad de modelar pagos acumulativos (\(S_{ij}\)) o incrementales (\(y_{ij}\)). Como aprendimos en los Capítulos 7 y 8 al estudiar series de tiempo, es útil poder modelar tanto una serie (\(S_{ij}\)) como sus cambios (\(y_{ij} = S_{ij} - S_{i,j-1}\)).
19.3.1 Modelo de Mack
El modelo propuesto por Mack (1993) especifica los dos primeros momentos condicionales de los pagos acumulativos y utiliza mínimos cuadrados generalizados para ajustar el modelo. Bajo esta especificación estocástica, se producen pronósticos tradicionales de escalera en cadena.
Específicamente, asumimos
\[\begin{equation} \mathrm{E} \left( S_{i,j} | S_{i,j-1} \right) = \nu_j S_{i,j-1} \tag{19.4} \end{equation}\] y \[\begin{equation} \mathrm{Var} \left( S_{i,j} | S_{i,j-1} \right) = \sigma^2_j S_{i,j-1}, \tag{19.5} \end{equation}\] donde \(\nu_j\) y \(\sigma^2_j\) son parámetros del modelo.
Los parámetros de media, \(\nu_j\), se determinan a través de mínimos cuadrados generalizados al minimizar la cantidad \[ Q = \sum_{j=2}^n \sum_{i=1}^{n+1-i} \frac{(S_{ij} - \nu_j S_{i,j-1})^2}{\sigma_j^2 S_{i,j-1}}. \] Tomando derivadas con respecto a los parámetros \(\nu_j\) y estableciendo estas igual a cero, se obtiene \[ \frac{\partial}{\partial \nu_j}Q = \sum_{i=1}^{n+1-i} \frac{(-2) (S_{ij} - \nu_j S_{i,j-1})}{\sigma_j^2 S_{i,j-1}} = 0. \] La solución de esta ecuación resulta en \[ \hat{\nu_j}= \frac{\sum_{i=1}^{n+1-i} S_{ij}} {\sum_{i=1}^{n+1-i} S_{i,j-1}}, \] el factor de escalera en cadena. Aquí, el símbolo “hat” o “sombrero” en \(\nu_j\) indica que \(\hat{\nu_j}\) es un estimador determinado por los datos.
Con estas estimaciones de parámetros, se puede utilizar la ecuación (19.4) para producir valores ajustados que son iguales a las estimaciones de la escalera en cadena. Además, se pueden estimar los parámetros de escala \(\sigma^2_j\) y luego usar la ecuación (19.5) para cuantificar la incertidumbre de las estimaciones. Consulte a England y Verrall (2002) o Wüthrich y Merz (2008) para obtener detalles sobre la estimación de parámetros de escala.
La fortaleza y limitación de este modelo es que solo emplea suposiciones sobre los dos primeros momentos condicionales. Es una fortaleza en el sentido de que no necesitamos preocuparnos si la distribución subyacente se acerca a lognormal o Poisson. Por lo tanto, a veces se lo denomina un modelo “no paramétrico”. Es una limitación en el sentido de que las medidas de incertidumbre en la ecuación (19.5) están relacionadas con el segundo momento que utiliza una función de pérdida de error cuadrático. Para reclamaciones de seguros, los datos suelen estar sesgados, por lo que la varianza no es una buena medida de escala. Además, en la reserva de pérdidas, queremos saber si las reservas son demasiado altas o demasiado bajas; usar una medida de incertidumbre que solo informe desviaciones absolutas no proporciona al actuario el tipo de información necesaria.
19.3.2 Modelos Distribucionales
Se han propuesto en la literatura modelos que complementan las suposiciones de momentos en las ecuaciones (19.4) y (19.5) con suposiciones distribucionales sobre los pagos.
Por ejemplo, Verrall propuso usar la binomial negativa como distribución para \(\{y_{ij}\}\) con momentos condicionales
\[ \mathrm{E} \left( y_{i,j} | S_{i,j-1} \right) = (\nu_j-1) S_{i,j-1} \] y \[ \mathrm{Var} \left( y_{i,j} | S_{i,j-1} \right) = \phi \nu_j (\nu_j -1) S_{i,j-1}, \] donde \(\phi\) y \(\nu_j\) son parámetros del modelo. Note que la suposición de media condicional es la misma que en la ecuación (19.4) debido a la relación \(\mathrm{E} \left( S_{i,j} | S_{i,j-1} \right) = S_{i,j-1} + \mathrm{E} \left( y_{i,j} | S_{i,j-1} \right)\). De manera similar, podemos expresar la varianza de los pagos acumulativos como \(\mathrm{Var} \left( S_{i,j} | S_{i,j-1} \right) = \mathrm{Var} \left( y_{i,j} | S_{i,j-1} \right)\). Por lo tanto, la suposición de varianza condicional es como en la ecuación (19.5) con parámetros \(\sigma^2_j = \phi \nu_j (\nu_j -1)\). Este modelo puede implementarse fácilmente utilizando software de modelos lineales generalizados especificando el modelo binomial negativo con función de enlace logarítmica \[ \ln \mu_{ij} = \ln \lambda_j + \ln S_{i,j-1}, \] donde \(\mu_{ij} = \mathrm{E} \left( y_{i,j} | S_{i,j-1} \right)\). Consulte England y Verrall (2002, Sección 7.3) para mayor discusión.
Otro modelo distribucional, sugerido por England y Verrall (2002, Sección 2.5), consiste en usar los momentos en las ecuaciones (19.4) y (19.5) pero especificar una distribución normal para los pagos \(\{y_{ij} \}\). Esto puede ser útil como una aproximación al modelo binomial negativo, particularmente en el caso cuando las estimaciones de \(\nu_j\) son menores a uno, lo que indica que la varianza condicional está mal especificada.
Como se enfatizó al comienzo de la Sección 19.2, las principales fortalezas de los modelos distribucionales son que (1) permiten a los analistas cuantificar la incertidumbre de los pronósticos y (2) proporcionan mecanismos disciplinados para la selección de modelos.
19.4 Lecturas Adicionales y Referencias
Dos introducciones extensas a los triángulos de reclamaciones son Taylor (2000) y Wüthrich y Merz (2008). Los actuarios en ejercicio encontrarán útil el artículo de revisión de England y Verrall (2002).
Cuando hay inestabilidad en los patrones de desarrollo en los primeros años, un método desarrollado por Bornheuetter y Ferguson (1972) puede ser útil, ya que permite al actuario incorporar una evaluación externa de las reclamaciones pagadas definitivas. Al igual que con la escalera en cadena, esta técnica puede expresarse en términos de modelado estocástico mediante modelado bayesiano. Vea, por ejemplo, la discusión de England y Verrall (2002), Wüthrich y Merz (2008) y de Alba (2006).
Un problema emergente es desarrollar reservas cuando un triángulo está correlacionado con otro. Tal correlación podría esperarse entre líneas de negocio de seguros. Braun (2004) proporciona una introducción a este tema.
Otra área emergente es desarrollar reservas basadas en patrones de desarrollo de reclamaciones individuales, como se describe en la Sección 19.1.1. Antonio et al. (2006) proporciona una introducción a este tema, donde usan modelos lineales mixtos para desarrollar reservas para reclamaciones que han sido reportadas pero aún no liquidadas. Vea también la Sección 14.5 sobre teoría de eventos recurrentes.
Referencias del Capítulo
- de Alba, Enrique (2006). Claims reserving when there are negative values in the runoff triangle: Bayesian analysis using the three-parameter log-normal distribution. North American Actuarial Journal 10 (3), 45-59.
- Antonio, Katrien, Jan Beirlant, Tom Hoedemakers and Robert Verlaak (2006). Lognormal mixed models for reported claim reserves. North American Actuarial Journal 10 (1), 30-48.
- Bornheuetter, Ronald L. and Ronald E. Ferguson (1972). The actuary and IBNR. Proceedings of the Casualty Actuarial Society 59, 181-195.
- Braun, Christian (2004). The prediction error of the chain ladder method applied to correlated run-off triangles. Astin Bulletin 34 (2), 399-423.
- England, Peter D. and Richard J. Verrall (2002). Stochastic claims reserving in general insurance. British Actuarial Journal 8, 443-544.
- Gamage, Jinadasa, Jed Linfield, Krzysztof Ostaszewski and Steven Siegel (2007). Statistical methods for health actuaries - IBNR estimates: An introduction. Society of Actuaries working paper, Society of Actuaries, Schaumburg IL.
- Mack, Thomas (1993). Distribution-free calculation of the standard error of chain-ladder reserve estimates. ASTIN Bulletin 23 (2), 213-225.
- Mack, Thomas (1994). Measuring the variability of chain-ladder reserve estimates. Casualty Actuarial Society, Spring Forum.
- Taylor, Greg (2000). Loss Reserving: An Actuarial Perspective. Kluwer Academic Publishers, Boston.
- Wacek, Michael G. (2007). The path of the ultimate loss ratio estimate. Variance 1(2), 173-192.
- Wüthrich, Mario V. and Michael Merz (2008). Stochastic Claims Reserving Methods in Insurance. Wiley, New York.
19.5 Ejercicios
19.1. Los datos en Tabla 19.5 provienen de la edición de 1991 del “Historical Loss Development Study” publicado por la Reinsurance Association of America (página 91). Estos datos se han utilizado ampliamente para ilustrar métodos de triángulo, comenzando con Mack (1994) y posteriormente por England y Verrall (2002). Estos datos provienen de negocios de reaseguro facultativo automático en coberturas de responsabilidad civil general (excluyendo asbesto y medio ambiente). (Bajo una base facultativa, cada riesgo es suscrito por el reasegurador según sus propios méritos). Tabla 19.5 reporta pérdidas incurridas incrementales de 1981 a 1990, en miles de dólares estadounidenses.
Comience calculando los factores determinísticos de la cadena en escalera. Note que el elemento en el segundo origen y el séptimo año de desarrollo es negativo. Puede que desee convertir primero los pagos incrementales en pagos acumulativos. Use estos factores para “completar el triángulo.”
Utilice su trabajo en la parte (a) para calcular la estimación de la reserva.
Elimine la observación en el segundo origen y el séptimo año de desarrollo. Ajuste un modelo lognormal a los datos restantes. Comente sobre la significancia estadística de cada factor y la bondad de ajuste.
Ajuste el modelo de Hoerl a los datos de la parte (c). Genere un gráfico de los valores ajustados.
Ajuste el modelo de Poisson sobredisperso a los datos de la parte (c). Verifique la proximidad de estos valores ajustados con los valores de la cadena en escalera producidos en la parte (a).
Tabla 19.5. Estudio de Desarrollo de Pérdidas (1991) Reaseguro Facultativo
\[ \small{ \begin{array}{crrrrrrrrrr} \hline \text{Año} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline 1 & 5,012 & 3,257 & 2,638 & 898 & 1,734 & 2,642 & 1,828 & 599 & 54 & 172 \\ 2 & 106 & 4,179 & 1,111 & 5,270 & 3,116 & 1,817 & -103 & 673 & 535 & \\ 3 & 3,410 & 5,582 & 4,881 & 2,268 & 2,594 & 3,479 & 649 & 603 & & \\ 4 & 5,655 & 5,900 & 4,211 & 5,500 & 2,159 & 2,658 & 984 & & & \\ 5 & 1,092 & 8,473 & 6,271 & 6,333 & 3,786 & 225 & & & & \\ 6 & 1,513 & 4,932 & 5,257 & 1,233 & 2,917 & & & & & \\ 7 & 557 & 3,463 & 6,926 & 1,368 & & & & & & \\ 8 & 1,351 & 5,596 & 6,165 & & & & & & & \\ 9 & 3,133 & 2,262 & & & & & & & & \\ 10 & 2,063 & & & & & & & & & \\ \hline \end{array} } \]
19.2. Los datos en Tabla 19.6 son un extracto de Braun (2004) basado en la edición de 2001 del “Historical Loss Development Study” publicado por la Reinsurance Association of America. Los datos más amplios (disponibles en el archivo “ReinsGL2004”) contienen datos de los años 1987-2000, inclusive.
Repita las partes (a)-(e) del Ejercicio 19.1 para estos datos.
Tabla 19.6. Reaseguro de Responsabilidad General
\[ \small{ \begin{array}{lrrrrrr} \hline \text{Año} & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 1995 & 97,518 & 343,218 & 575,441 & 769,017 & 934,103 & 1,019,303 \\ 1996 & 173,686 & 459,416 & 722,336 & 955,335 & 1,141,750 & \\ 1997 & 139,821 & 436,958 & 809,926 & 1,174,196 & & \\ 1998 & 154,965 & 528,080 & 1,032,684 & & & \\ 1999 & 196,124 & 772,971 & & & & \\ 2000 & 204,325 & & & & & \\ \hline \end{array} } \]
19.3. Los datos en Tabla 19.7 provienen de Wacek (2007). Los datos representan agregados de la industria para coberturas de responsabilidad civil y médicas de automóviles particulares del año 2004, en millones de dólares. Están basados en los estados anuales de las compañías de seguros, específicamente, en el Anexo P, Parte 3B. Los elementos del triángulo representan pagos netos acumulados, incluidos los gastos de defensa y contención de costos.
Repita las partes (a)-(e) del Ejercicio 19.1 para estos datos.
Tabla 19.7. 2004 Agregados de la Industria de Seguros de los EE. UU. para Responsabilidad Civil y Médica de Automóviles Particulares
\[ \small{ \begin{array}{rrrrrrrrrrr} \hline \text{Año} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline 1995 & 17,674 & 32,062 & 38,619 & 42,035 & 43,829 & 44,723 & 45,162 & 45,375 & 45,483 & 45,540 \\ 1996 & 18,315 & 32,791 & 39,271 & 42,933 & 44,950 & 45,917 & 46,392 & 46,600 & 46,753 & \\ 1997 & 18,606 & 32,942 & 39,634 & 43,411 & 45,428 & 46,357 & 46,681 & 46,921 & & \\ 1998 & 18,816 & 33,667 & 40,575 & 44,446 & 46,476 & 47,350 & 47,809 & & & \\ 1999 & 20,649 & 36,515 & 43,724 & 47,684 & 49,753 & 50,716 & & & & \\ 2000 & 22,327 & 39,312 & 46,848 & 51,065 & 53,242 & & & & & \\ 2001 & 23,141 & 40,527 & 48,284 & 52,661 & & & & & & \\ 2002 & 24,301 & 42,168 & 50,356 & & & & & & & \\ 2003 & 24,210 & 41,640 & & & & & & & & \\ 2004 & 24,468 & & & & & & & & & \\ \hline \end{array} } \]
19.4. Los datos en Tabla 19.8 provienen de Gamage et al. (2007). Estos datos corresponden a 36 meses de pagos de atención médica, desde enero de 2001 hasta diciembre de 2003, inclusive. Estos son pagos por cobertura médica sin deducible ni coseguro. Los copagos eran relativamente bajos, como $10 por visita al consultorio. Los pagos excluyen medicamentos recetados, que generalmente tienen un patrón de pago más corto en comparación con otras reclamaciones médicas.
Repita las partes (a)-(e) del Ejercicio 19.1 para estos datos.
Tabla 19.8. Pagos Mensuales de Atención Médica, 2001-2003
\[ \begin{array}{lrcrrrrrrrrrrrrr} \hline \text{Fecha} & \text{Miembros} & \text{ Mes} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 \\ \hline Ene-01 & 11,154 & 1 & 180 & 436,082 & 933,353 & 116,978 & 42,681 & 41,459 & 5,088 & 22,566 & 4,751 & 3,281 & -188 & 1,464 & 1,697 \\ Feb-01 & 11,118 & 2 & 5,162 & 940,722 & 561,967 & 21,694 & 171,659 & 11,008 & 19,088 & 5,213 & 4,337 & 7,844 & 2,973 & 4,061 & 10,236 \\ Mar-01 & 11,070 & 3 & 42,263 & 844,293 & 720,302 & 94,634 & 182,077 & 32,216 & 12,937 & 22,815 & 1,754 & 4,695 & 1,326 & 758 & 2,177 \\ Abr-01 & 11,069 & 4 & 20,781 & 762,302 & 394,625 & 78,043 & 157,950 & 46,173 & 126,254 & 4,839 & 337 & 1,573 & 9,573 & 1,947 & 5,937 \\ May-01 & 11,130 & 5 & 20,346 & 772,404 & 392,330 & 315,888 & 39,197 & 21,360 & 8,721 & 5,452 & 16,627 & 2,118 & 4,119 & 5,666 & -1,977 \\ Jun-01 & 11,174 & 6 & 20,491 & 831,793 & 738,087 & 65,526 & 27,768 & 12,185 & 1,493 & 11,265 & 1,805 & 29,278 & 13,020 & 2,967 & -83 \\ Jul-01 & 11,180 & 7 & 37,954 & 1,126,675 & 360,514 & 89,317 & 40,126 & 16,576 & 16,701 & 2,444 & 8,266 & 11,310 & 8,006 & 1,403 & 3,124 \\ Aug-01 & 11,420 & 8 & 138,558 & 806,362 & 589,304 & 273,117 & 36,912 & 16,831 & 19,941 & 13,310 & 8,619 & 4,679 & 3,094 & 4,609 & 236 \\ Sep-01 & 11,400 & 9 & 28,332 & 954,543 & 246,571 & 205,528 & 60,060 & 15,198 & 42,208 & 17,568 & 1,686 & 9,897 & 3,367 & 2,062 & 421 \\ Oct-01 & 11,456 & 10 & 104,160 & 704,796 & 565,939 & 323,789 & 45,307 & 32,518 & 26,227 & 7,976 & 3,364 & 992 & 33,963 & 2,200 & 1,293 \\ Nov-01 & 11,444 & 11 & 40,747 & 927,158 & 425,794 & 146,145 & 66,663 & 31,214 & 12,808 & 15,859 & 374 & 3,079 & 412 & 937 & 1,875 \\ Dic-01 & 11,555 & 12 & 10,861 & 847,338 & 272,165 & 134,798 & 71,804 & 27,800 & 17,917 & 3,930 & 2,794 & 846 & 1,962 & 1,879 & 16,060 \\ Ene-02 & 11,705 & 13 & 77,938 & 896,195 & 544,372 & 173,606 & 41,595 & 4,209 & 16,473 & 6,000 & -66 & -1,881 & -4,054 & 84,233 & 4,921 \\ Feb-02 & 11,823 & 14 & 38,041 & 1,035,439 & 438,153 & 115,587 & 12,489 & 22,260 & 13,203 & 6,395 & 2,056 & -3,323 & 33,397 & 3,479 & -1,625 \\ Mar-02 & 11,753 & 15 & 39,410 & 1,022,024 & 255,002 & 169,881 & 35,230 & 40,307 & 21,067 & 5,378 & 5,508 & 17,606 & -24,320 & 1,298 & 1,362 \\ Abr-02 & 11,654 & 16 & 68,253 & 1,414,379 & 317,110 & 91,880 & 53,970 & 10,888 & 3,171 & 11,660 & 20,861 & 1,033 & -21,670 & 2,634 & 149 \\ May-02 & 11,703 & 17 & 124,824 & 1,053,972 & 516,876 & 145,954 & 25,171 & 12,609 & 7,704 & 29,633 & 4,555 & 6,203 & 3,872 & 1,116 & 666 \\ Jun-02 & 11,580 & 18 & 49,725 & 1,119,099 & 533,444 & 80,182 & 32,203 & 23,205 & 18,807 & 7,944 & 4,152 & -910 & 3,664 & 608 & 528 \\ Jul-02 & 11,577 & 19 & 44,317 & 1,297,335 & 385,789 & 141,155 & 150,726 & 35,075 & 16,176 & 8,070 & 67 & 14,217 & 2,326 & 7,091 & 687 \\ Aug-02 & 11,655 & 20 & 134,152 & 1,111,151 & 493,175 & 101,439 & 46,657 & 22,824 & 12,818 & 3,781 & 1,265 & 2,467 & -62,165 & 247 & -8,689 \\ Sep-02 & 11,735 & 21 & 29,968 & 1,382,043 & 178,587 & 71,030 & 25,708 & 15,068 & 3,145 & -4,058 & -1,920 & 4,984 & -1,523 & -3,539 & -478 \\ Oct-02 & 11,889 & 22 & 210,377 & 999,963 & 528,880 & 201,410 & 58,003 & 26,174 & -9,371 & 2,017 & 9,795 & 6,688 & -40 & 453 & -73 \\ Nov-02 & 11,951 & 23 & 56,654 & 1,206,370 & 376,504 & 56,322 & 19,591 & 12,055 & 21,077 & 11,573 & 4,039 & 822 & 6,612 & -9,678 & 715 \\ Dic-02 & 12,132 & 24 & 89,181 & 1,240,938 & 279,553 & 57,164 & 75,344 & 12,665 & 71,741 & 9,049 & 1,298 & 12,164 & 19,616 & -4,604 & -3,184 \\ Ene-03 & 12,227 & 25 & 131,568 & 1,301,927 & 716,180 & 150,253 & 110,031 & 78,148 & 4,610 & 19,855 & 18,448 & 14,432 & 119 & 2,748 & \\ Feb-03 & 12,201 & 26 & 76,262 & 1,130,312 & 692,736 & 174,283 & 38,891 & 41,811 & 8,834 & 18,123 & 4,268 & -291 & 2,119 & & \\ Mar-03 & 12,130 & 27 & 159,575 & 1,313,809 & 704,116 & 68,412 & 30,185 & 64,402 & 19,229 & -3,021 & 3,220 & 1,994 & & & \\ Abr-03 & 11,986 & 28 & 76,313 & 1,505,842 & 437,084 & 50,872 & 116,723 & 18,160 & 10,975 & 12,664 & 8,805 & & & & \\ May-03 & 11,927 & 29 & 104,028 & 1,667,823 & 360,676 & 153,274 & 37,529 & 34,840 & 17,479 & 9,374 & & & & & \\ Jun-03 & 11,814 & 30 & 79,688 & 1,235,573 & 776,240 & 65,303 & 18,723 & 10,779 & 10,615 & & & & & & \\ Jul-03 & 11,787 & 31 & 76,395 & 1,689,354 & 442,965 & 234,171 & 36,806 & 22,351 & & & & & & & \\ Aug-03 & 11,689 & 32 & 110,460 & 1,492,980 & 589,184 & 93,366 & 180,095 & & & & & & & & \\ Sep-03 & 11,731 & 33 & 196,687 & 2,011,979 & 313,416 & 166,839 & & & & & & & & & \\ Oct-03 & 11,843 & 34 & 268,365 & 1,027,925 & 897,097 & & & & & & & & & & \\ Nov-03 & 11,902 & 35 & 58,510 & 1,225,307 & & & & & & & & & & & \\ Dic-03 & 11,844 & 36 & 96,378 & & & & & & & & & & & & \\ \hline \hline \end{array} \]