Capítulo 17 Modelos de Regresión con Colas Gruesas

Vista Previa del Capítulo. Al modelar cantidades financieras, estamos tan interesados en los valores extremos como en el centro de la distribución; estos valores extremos pueden representar las reclamaciones, ganancias o ventas más inusuales. Los actuarios frecuentemente encuentran situaciones donde los datos presentan “colas gruesas,” lo que significa que los valores extremos en los datos son más probables que en los datos normalmente distribuidos. La regresión tradicional se centra en el centro de la distribución y minimiza la importancia de los valores extremos. En contraste, el enfoque de este capítulo es sobre toda la distribución. Este capítulo examina cuatro técnicas para el análisis de regresión de datos con colas gruesas: transformaciones, modelos lineales generalizados, distribuciones más generales y regresión cuantílica.

17.1 Introducción

Los actuarios frecuentemente encuentran situaciones donde los datos presentan “colas gruesas,” lo que significa que los valores extremos en los datos son más probables que en los datos normalmente distribuidos. Estas distribuciones pueden describirse como “gruesas,” “pesadas,” “anchas” o “largas” en comparación con la distribución normal. (La Sección 17.3.1 será más precisa sobre qué constituye una “cola gruesa.”) En finanzas, por ejemplo, las teorías de precios de activos CAPM y APT asumen retornos de activos normalmente distribuidos. Sin embargo, las distribuciones empíricas de los retornos de activos financieros sugieren distribuciones con colas gruesas en lugar de distribuciones normales, como asumen las teorías de precios (ver, por ejemplo, Rachev, Menn y Fabozzi, 2005). En el área de la salud, los datos con colas gruesas también son comunes. Por ejemplo, los resultados de interés como el número de días de hospitalización o los gastos hospitalarios suelen ser asimétricos a la derecha y de colas pesadas debido a unos pocos pacientes de alto costo (Basu, Manning y Mullahy, 2004). Los actuarios también analizan regularmente datos con colas gruesas en el seguro de no vida (Klugman, Panjer y Willmot, 2008).

Como ocurre con cualquier otro conjunto de datos, el resultado de interés puede estar relacionado con otros factores, por lo que el análisis de regresión es de interés. Sin embargo, emplear rutinas de regresión habituales sin abordar la naturaleza de las colas gruesas puede conducir a serias dificultades.

  • Los coeficientes de regresión pueden expresarse como sumas ponderadas de las variables dependientes. Por lo tanto, los coeficientes pueden ser influenciados indebidamente por observaciones extremas.
  • Debido a que la distribución tiene colas gruesas, las reglas generales de aproximación (muestras grandes) a la normalidad de los estimadores de parámetros ya no se aplican. Por ejemplo, los \(t\)-ratios estándar y los valores-\(p\) asociados con los estimadores de regresión pueden no ser indicadores significativos de significancia estadística.
  • Las rutinas de regresión usuales minimizan una función de pérdida de error cuadrático. Para algunos problemas, nos preocupan más los errores en una dirección (ya sean pequeños o grandes), no una función simétrica.
  • Los valores grandes en el conjunto de datos pueden ser los más importantes en un sentido financiero, por ejemplo, un gasto extremadamente alto al examinar costos médicos. Aunque atípico, no es una observación que deseemos descuidar ni desestimar simplemente porque no se ajusta al modelo de regresión basado en la normalidad.

Este capítulo describe cuatro enfoques básicos para manejar datos de regresión con colas gruesas:

  • transformaciones de la variable dependiente,
  • modelos lineales generalizados,
  • modelos que utilizan distribuciones positivas más flexibles, como la gamma generalizada, y
  • modelos de regresión cuantílica.

Las Secciones 17.2-17.5 abordan cada enfoque.

Otro campo de la estadística dedicado al análisis del comportamiento en las colas es conocido como “estadística de valores extremos.” Este campo se centra en modelar el comportamiento en las colas, en gran medida a expensas de ignorar el resto de la distribución. En contraste, la regresión tradicional se enfoca en el centro de la distribución y minimiza la importancia de los valores extremos. Para las cantidades financieras, estamos tan interesados en los extremos como en el centro de la distribución; estos valores extremos pueden representar las reclamaciones, ganancias o ventas más inusuales. El enfoque de este capítulo es sobre toda la distribución. La modelación de regresión dentro de la estadística de valores extremos es un tema que apenas ha comenzado a recibir atención seria; la Sección 17.6 proporciona un breve resumen.

17.2 Transformaciones

Como hemos visto a lo largo de este texto, el enfoque más utilizado para manejar datos con colas gruesas es simplemente transformar la variable dependiente. Como práctica habitual, los analistas toman una transformación logarítmica de \(y\) y luego utilizan mínimos cuadrados ordinarios en \(\ln (y)\). Aunque esta técnica no siempre es apropiada, ha resultado efectiva para un sorprendente número de conjuntos de datos. Esta sección resume lo que hemos aprendido sobre transformaciones y proporciona algunas herramientas adicionales que pueden ser útiles en ciertas aplicaciones.

La Sección 1.3 introdujo la idea de las transformaciones y mostró cómo las transformaciones de potencia podían usarse para simetrizar una distribución. Las transformaciones de potencia, como \(y^{\lambda}\), pueden “ajustar” los valores extremos para que ninguna observación tenga un efecto indebido en los estimadores de parámetros. Además, las reglas generales para la aproximación a la normalidad de los estimadores de parámetros son más aplicables cuando los datos son aproximadamente simétricos (en comparación con datos sesgados).

Sin embargo, existen tres principales desventajas en las transformaciones. La primera es que puede ser difícil interpretar los coeficientes de regresión resultantes. Una de las principales razones por las cuales introdujimos la transformación logarítmica natural en la Sección 3.2.2 fue su capacidad para proporcionar interpretaciones de los coeficientes de regresión como cambios proporcionales. Otras transformaciones pueden no disfrutar de esta interpretación intuitivamente atractiva.

La segunda desventaja, introducida en la Sección 5.7.4, es que una transformación también afecta otros aspectos del modelo, como la heterocedasticidad. Por ejemplo, si el modelo original es un modelo multiplicativo (heterocedástico) de la forma \(y_i=(\mathrm{E}y_i)~\varepsilon_i\), entonces una transformación logarítmica significa que el nuevo modelo es:

\[ \ln y_i=\ln \mathrm{E}(y_i)~+\ln \varepsilon_i. \]

A menudo, la capacidad de estabilizar la varianza se considera un aspecto positivo de las transformaciones. Sin embargo, el punto es que una transformación afecta tanto la simetría como la heterocedasticidad, cuando solo un aspecto podría considerarse problemático.

La tercera desventaja de transformar la variable dependiente es que el analista está optimizando implícitamente en la escala transformada. Esto ha sido considerado negativamente por algunos académicos. Como señaló Manning (1998), “… nadie está interesado en los resultados de un modelo logarítmico por sí mismos. El Congreso no asigna dólares logarítmicos.”

Nuestras discusiones sobre transformaciones se refieren a funciones de las variables dependientes. Como hemos visto en la Sección 3.5, es común transformar variables explicativas. El adjetivo “lineal” en la frase “regresión lineal múltiple” se refiere a combinaciones lineales de parámetros; las variables explicativas en sí mismas pueden ser altamente no lineales.

Otra técnica que hemos utilizado implícitamente a lo largo del texto para manejar datos con colas gruesas se conoce como reescalado. En el reescalado, se divide la variable dependiente por una variable explicativa para que el cociente resultante sea más comparable entre observaciones. Por ejemplo, en la Sección 6.5 utilizamos primas de seguros de bienes y accidentes y pérdidas no aseguradas divididas por activos como la variable dependiente. Aunque el numerador, un proxy para los gastos anuales asociados con eventos asegurables, es la medida clave de interés, es común estandarizar por el tamaño de la empresa (medido por activos).

Muchas transformaciones son casos especiales de la familia de transformaciones de Box-Cox, introducida en la Sección 1.3. Recuerde que esta familia se define como:

\[ y^{(\lambda)}=\left\{ \begin{array}{ll} \frac{y^{\lambda }-1}{\lambda } & \mathrm{si}~\lambda \neq 0 \\ \ln y & \mathrm{si}~\lambda =0 \end{array} \right. , \]

donde \(\lambda\) es el parámetro de transformación (típicamente \(\lambda =1,1/2,0~ \mathrm{o}~-1\)). Cuando los datos son no positivos, es común agregar una constante a cada observación para que todas las observaciones sean positivas antes de la transformación. Por ejemplo, la transformación \(\ln (1+y)\) acomoda la presencia de ceros. También se puede multiplicar por una constante para que se retengan las unidades originales aproximadas. Por ejemplo, la transformación \(100\ln (1+y/100)\) puede aplicarse a datos porcentuales donde a veces aparecen porcentajes negativos. Para las distribuciones binomial, de Poisson y gamma, también mostramos cómo usar transformaciones de potencia para aproximar la normalidad y la estabilización de la varianza en la Sección 13.5.

De manera alternativa, para manejar datos no positivos, una modificación fácil de usar es la transformación logarítmica con signo, dada por \(\mathrm{sign}(y) \ln(|y|+1)\). Este es un caso especial de la familia introducida por John y Draper (1980):

\[ y^{(\lambda)}=\left\{ \begin{array}{lr} \mathrm{sign}(y) \left\{(|y|+1)^\lambda-1\right\}/\lambda, & \lambda \neq 0 \\ \mathrm{sign}(y) \ln(|y|+1),& \lambda=0 \end{array} \right. . \]

Una desventaja de la familia de John y Draper es que su derivada no es continua en cero, lo que significa que puede haber discontinuidades abruptas para observaciones cercanas a cero. Para abordar esto, Yeo y Johnson (2000) recomiendan la siguiente extensión de la familia Box-Cox:

\[ y^{(\lambda )}=\left\{ \begin{array}{ll} \frac{(1+y)^{\lambda }-1}{\lambda } & y\geq 0,\lambda \neq 0 \\ \ln (1+y) & y\geq 0,\lambda =0 \\ -\frac{(1+|y|)^{2-\lambda }-1}{2-\lambda } & y<0,\lambda \neq 2 \\ -\ln (1+|y|) & y<0,\lambda =2 \end{array} \right. . \]

Para valores no negativos de \(y\), esta transformación es igual a la familia Box-Cox utilizando \(1+y\) en lugar de \(y\) para acomodar ceros. Para valores negativos, la potencia \(\lambda\) se reemplaza por \(2-\lambda\), de modo que una distribución asimétrica a la derecha permanece asimétrica a la derecha después del cambio de signo. La Figura 17.1 muestra esta función para varios valores de \(\lambda\).

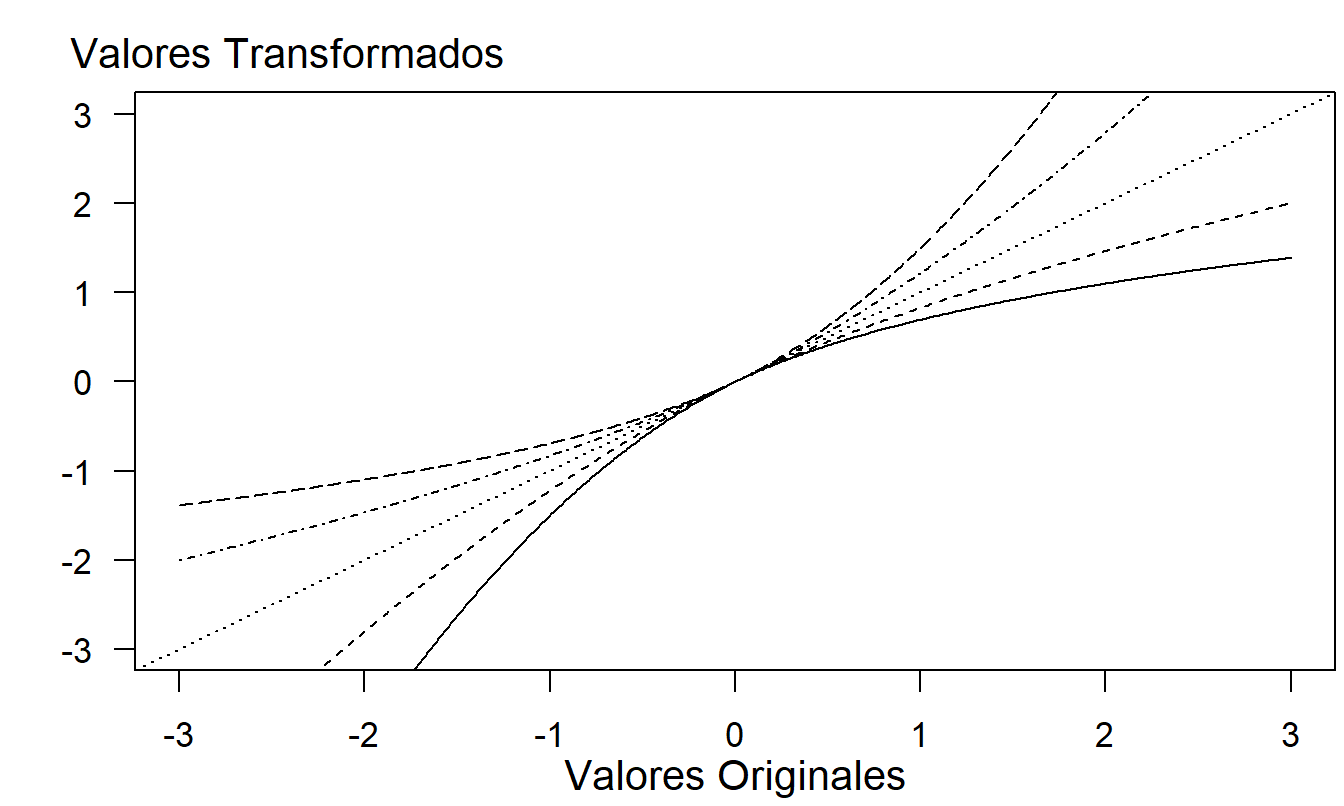
Transformaciones de Yeo-Johnson. De abajo hacia arriba, las curvas corresponden a \(\lambda =0,0.5,1,1.5\) y 2.

Figura 17.1: Transformaciones de Yeo-Johnson. De abajo hacia arriba, las curvas corresponden a \(\lambda =0,0.5,1,1.5\) y 2.

Tanto la familia de John y Draper como la de Yeo y Johnson se basan en transformaciones de potencia. Una familia alternativa, propuesta por Burbidge y Magee (1988), es una modificación de la transformación de seno hiperbólico inverso. Esta familia se define como: \[ y^{(\lambda)}=\sinh^{-1}(\lambda y)/\lambda . \]

17.3 Modelos Lineales Generalizados

Como se introdujo en el Capítulo 13, el método de modelos lineales generalizados (GLM) se ha vuelto popular en las estadísticas financieras y actuariales. Una ventaja de esta metodología es la capacidad de ajustar distribuciones con colas más pesadas que la distribución normal. En particular, los métodos GLM se basan en la familia exponencial que incluye las distribuciones normal, gamma e inversa gaussiana. Como veremos en la Sección 17.3.1, es común considerar que la distribución gamma tiene colas intermedias y la inversa gaussiana colas pesadas en comparación con la distribución normal de cola delgada.

La idea de un GLM es mapear un componente sistemático lineal \(\mathbf{x}^{\prime }\boldsymbol \beta\) en la media de la variable de interés a través de una función conocida. Así, los GLM proporcionan una forma natural de incluir covariables en el modelado. Con un GLM, no se requiere que la varianza sea constante como en el modelo lineal, sino que es una función de la media. Una vez que se han especificado la familia de distribución y la función de enlace, la estimación de los coeficientes de regresión del GLM depende únicamente de la media y, por lo tanto, es robusta a algunas especificaciones incorrectas del modelo de distribución. Esto es tanto una fortaleza como una debilidad del enfoque GLM. Aunque más flexible que el modelo lineal, este enfoque no maneja muchas de las distribuciones de colas largas tradicionalmente utilizadas para modelar datos de seguros. Por lo tanto, en la Sección 17.4 presentaremos distribuciones más flexibles.

17.3.1 ¿Qué significa “Cola Gruesa”?

Muchos analistas comienzan las discusiones sobre la pesadez de colas a través de los coeficientes de asimetría y curtosis. La asimetría mide la falta de simetría, o el sesgo, de una distribución. Se cuantifica típicamente por el tercer momento estandarizado, \(\mathrm{E}(y-\mathrm{E~}y)^3/ (\mathrm{Var~}y)^{3/2}.\) La curtosis mide la pesadez de las colas, o su inverso, la “puntiagudez.” Se cuantifica típicamente por el cuarto momento estandarizado menos 3, \(\mathrm{E}(y-\mathrm{E~}y)^4/ (\mathrm{Var~}y)^{2} -3.\) El “menos 3” es para centrar las discusiones en torno a la distribución normal; es decir, para una distribución normal, se puede comprobar que \(\mathrm{E}(y-\mathrm{E~}y)^4/(\mathrm{Var~}y)^{2} =3.\) Las distribuciones con curtosis positiva se denominan leptocúrticas mientras que aquellas con curtosis negativa se denominan platicúrticas. Estas definiciones se centran fuertemente en la normal, que tradicionalmente se ha considerado como la distribución de referencia.

Para muchas aplicaciones actuariales y financieras, la distribución normal no es un punto de partida adecuado, por lo que buscamos otras definiciones de “cola gruesa.” Además de los momentos, el tamaño de la cola puede medirse utilizando una función de densidad (o masa, para distribuciones discretas), la función de supervivencia, o un momento condicional. Típicamente, la medida se usaría para comparar una distribución con otra.

Por ejemplo, al comparar las colas derechas de la normal con una función de densidad gamma, tenemos: \[ \begin{array}{ll} \frac{\mathrm{f}_{normal}\left( y\right) }{\mathrm{f}_{gamma}\left( y\right) } &=\frac{\sqrt{2\pi \sigma ^{2}}\exp \left( -\left( y-\mu \right) ^{2}/(2\sigma ^{2})\right) }{\left[ \lambda ^{\alpha }\Gamma \left( \alpha \right) \right] ^{-1}y^{\alpha -1}\exp \left( -y/\lambda \right) } \\ &=C_1 ~\mathit{\exp }\left( -(\alpha -1)\ln y+y/\lambda -\left( y-\mu \right) /(2\sigma ^{2})\right) \\ &\rightarrow 0, \end{array} \] cuando \(y \rightarrow \infty\), lo que indica que la gamma tiene una cola más pesada, o gruesa, que la normal.

Tanto la normal como la gamma son miembros de la familia exponencial de distribuciones. Para una comparación con otro miembro de esta familia, la distribución inversa gaussiana, consideremos: \[ \begin{array}{ll} \frac{\mathrm{f}_{gamma}\left( y\right) }{\mathrm{f}_{invGaussian}\left( y\right) } &=\frac{\left[ \lambda ^{\alpha }\Gamma \left( \alpha \right) \right] ^{-1}y^{\alpha -1}\exp \left( -y/\lambda \right) }{\sqrt{\theta /(2\pi y^{3})}\exp \left( -\theta \left( y-\mu \right) ^{2}/(2y\mu ^{2})\right) } \\ &=C_2 ~\mathit{\exp }\left( (\alpha +1/2)\ln y-y/\lambda +\theta \left( y-\mu \right) ^{2}/(2y\mu ^{2}))\right) . \end{array} \] Cuando \(y\rightarrow \infty\), esta razón tiende a cero para \(\theta /(2\mu ^{2})<\lambda\), lo que indica que la inversa gaussiana puede tener una cola más pesada que la gamma.

Para una distribución que no es miembro de la familia exponencial, consideremos la distribución Pareto. Cálculos similares muestran: \[ \begin{array}{ll} \frac{\mathrm{f}_{gamma}\left( y\right) }{\mathrm{f}_{Pareto}\left( y\right) } &=\frac{\left[ \lambda ^{\alpha }\Gamma \left( \alpha \right) \right] ^{-1}y^{\alpha -1}\exp \left( -y/\lambda \right) }{\alpha \theta ^{-\alpha }\left( y+\theta \right) ^{-\alpha -1}} \\ &=C_3 ~\mathit{\exp }\left( (\alpha -1)\ln y-y/\lambda +\left( \alpha +1\right) \ln \left( y+\theta \right) \right) \\ & \rightarrow 0, \end{array} \] cuando \(y\rightarrow \infty\), lo que indica que la Pareto tiene una cola más pesada que la gamma.

La razón de densidades es una medida fácilmente interpretable para comparar la pesadez de colas de dos distribuciones. Debido a que las densidades y las funciones de supervivencia tienen un valor límite de cero, por la regla de L’Hôpital, la razón de funciones de supervivencia es equivalente a la razón de densidades. Es decir, \[ \lim_{y\rightarrow \infty }\frac{\mathrm{S}_1\left( y\right) }{\mathrm{S} _2\left( y\right) }=\lim_{y\rightarrow \infty }\frac{\mathrm{S} _1^{\prime }\left( y\right) }{\mathrm{S}_2^{\prime }\left( y\right) } = \lim_{y\rightarrow \infty }\frac{\mathrm{f}_1 \left( y\right) }{\mathrm{f}_2 \left( y\right) }. \] Esto proporciona otra motivación para usar esta medida.

17.3.2 Aplicación: Asilos de Ancianos en Wisconsin

La financiación de asilos de ancianos ha llamado la atención de los responsables políticos e investigadores durante las últimas décadas. Con poblaciones envejecidas y una mayor esperanza de vida, se espera que los gastos en asilos de ancianos y las demandas de atención a largo plazo aumenten en el futuro. En esta sección, analizamos los datos de 349 instalaciones de cuidado de ancianos en el estado de Wisconsin para el año fiscal 2001.

El programa de Medicaid del estado de Wisconsin financia el cuidado en asilos de ancianos para individuos que califican según su necesidad y situación financiera. La mayoría, pero no todos, los asilos de ancianos en Wisconsin están certificados para proporcionar atención financiada por Medicaid. Aquellos que no aceptan Medicaid generalmente son pagados directamente por el residente o su aseguradora.

De manera similar, la mayoría, pero no todos, los asilos de ancianos están certificados para proporcionar atención financiada por Medicare. Medicare proporciona atención post-aguda durante 100 días después de una hospitalización relacionada. Medicare no financia la atención proporcionada por instalaciones de cuidado intermedio para personas con discapacidades del desarrollo. Como parte de las condiciones para participar, los asilos de ancianos certificados por Medicare deben presentar un informe anual de costos al Departamento de Salud y Servicios Familiares de Wisconsin, que resume el volumen y costo de la atención proporcionada a todos sus residentes, ya sea financiada por Medicare o no.

Los asilos de ancianos son propiedad y están operados por una variedad de entidades, incluidos el estado, condados, municipios, negocios con fines de lucro y organizaciones exentas de impuestos. Las empresas privadas a menudo poseen varios asilos de ancianos. Periódicamente, las instalaciones pueden cambiar de propietario y, con menos frecuencia, de tipo de propiedad.

Típicamente, la utilización de la atención en asilos de ancianos se mide en días de paciente. Las instalaciones facturan al intermediario fiscal al final de cada mes por los días de paciente totales incurridos en el mes, desglosados por residente y nivel de atención. Las proyecciones de días de paciente por instalación y nivel de atención juegan un papel clave en el proceso anual de actualización de las tarifas de las instalaciones. Rosenberg et al. (2007) proporciona una discusión adicional.

Resumen de los Datos

Después de examinar los datos, encontramos algunas variaciones menores en el número de días que una instalación estuvo abierta, principalmente debido a aperturas y cierres de instalaciones. Por lo tanto, para hacer más comparable la utilización entre instalaciones, examinamos TPY, definido como el número total de días-paciente dividido por el número de días que la instalación estuvo abierta; esto tiene un valor mediano de 81.99 por instalación.

La Tabla 17.1 describe las variables que se utilizarán para explicar la distribución de TPY. Más de la mitad de las instalaciones tienen autofinanciamiento del seguro. Aproximadamente el \(90.5\%\) de las instalaciones están certificadas por Medicare. En cuanto a la estructura organizacional, cerca de la mitad \((51.9\%)\) son gestionadas con fines de lucro, alrededor de un tercio \((37.5\%)\) están organizadas como exentas de impuestos y el resto son organizaciones gubernamentales. Las instalaciones exentas de impuestos tienen las tasas de ocupación medianas más altas. Un poco más de la mitad de las instalaciones están ubicadas en un entorno urbano (53.3%).

Tabla 17.1: Estadísticas Descriptivas de los Asilos de Ancianos
Variable Descripción
TPY Años-persona totales (mediana 81.89)
NumBed Número de camas (mediana 90)
SqrFoot Superficie neta del asilo (en miles, mediana 40.25)
Variables explicativas categóricas Porcentaje Mediana TPY
POPID Número de identificación del asilo
SelfIns Autofinanciamiento del seguro
Sí 62.8 88.4
No 37.2 67.84
MCert Certificado por Medicare
Sí 90.5 84.06
No 9.5 53.38
Organizacional Pro (con fines de lucro) 51.9 77.23
Estructura TaxExempt (exento de impuestos) 37.5 81.13
Govt (unidad gubernamental) 10.6 106.7
Ubicación Urbana 53.3 91.55
Rural 46.7 74.12

Ajuste de Modelos Lineales Generalizados

La Figura 17.2 muestra la distribución de la variable dependiente TPY. En esta figura, vemos evidencia clara de la asimetría hacia la derecha de la distribución. Una opción sería realizar una transformación como se describe en la Sección 17.2. Rosenberg et al. (2007) exploraron esta opción utilizando una transformación logarítmica.

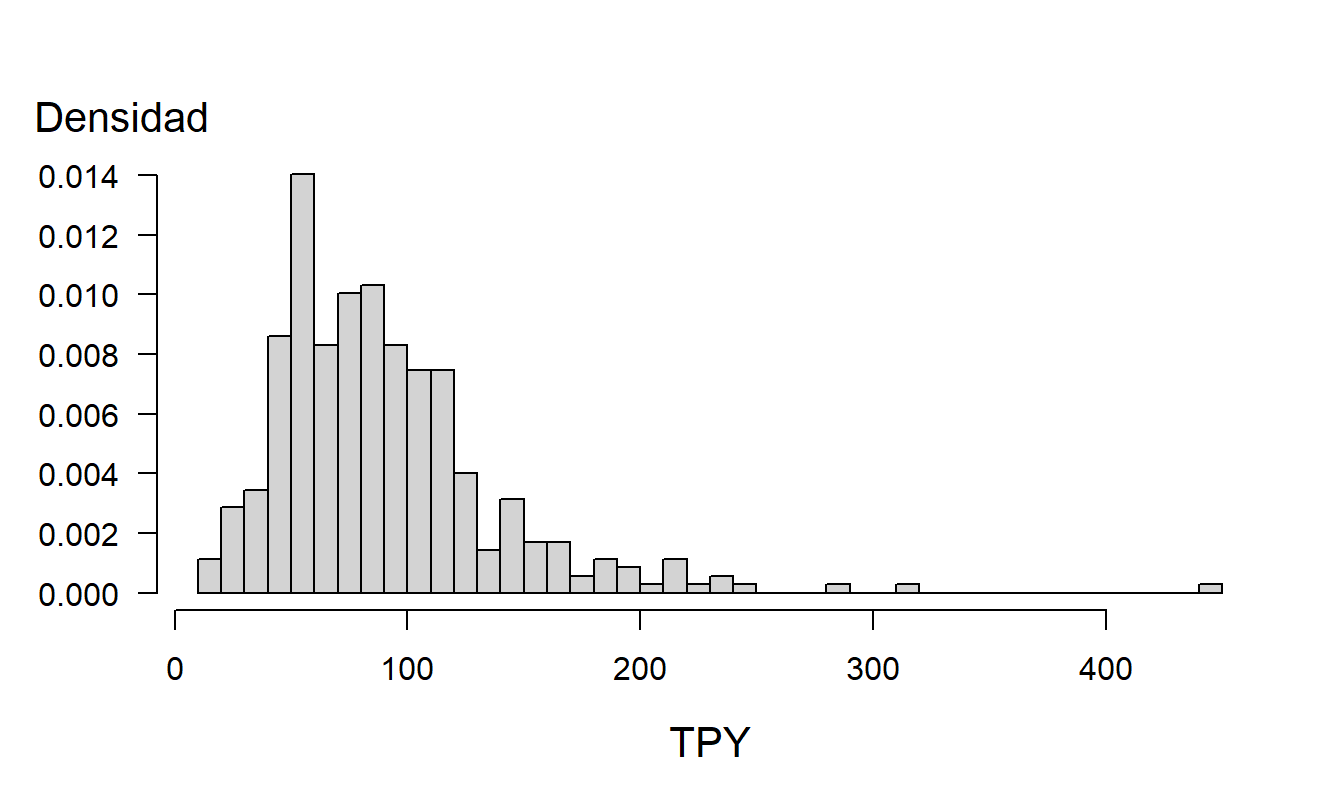
Histograma de TPY. Este gráfico demuestra la asimetría hacia la derecha de la distribución.

Figura 17.2: Histograma de TPY. Este gráfico demuestra la asimetría hacia la derecha de la distribución.

Código R para Producir Figura 17.2

Otra opción es ajustar directamente una distribución sesgada a los datos. La Figura 17.3 presenta los gráficos \(qq\) para las distribuciones gamma e inversa gaussiana. Los datos caen bastante cerca de la línea en ambos paneles, lo que indica que ambos modelos son elecciones razonables. El gráfico \(qq\) para la distribución normal, no mostrado aquí, indica que el modelo de regresión normal no es un ajuste razonable.

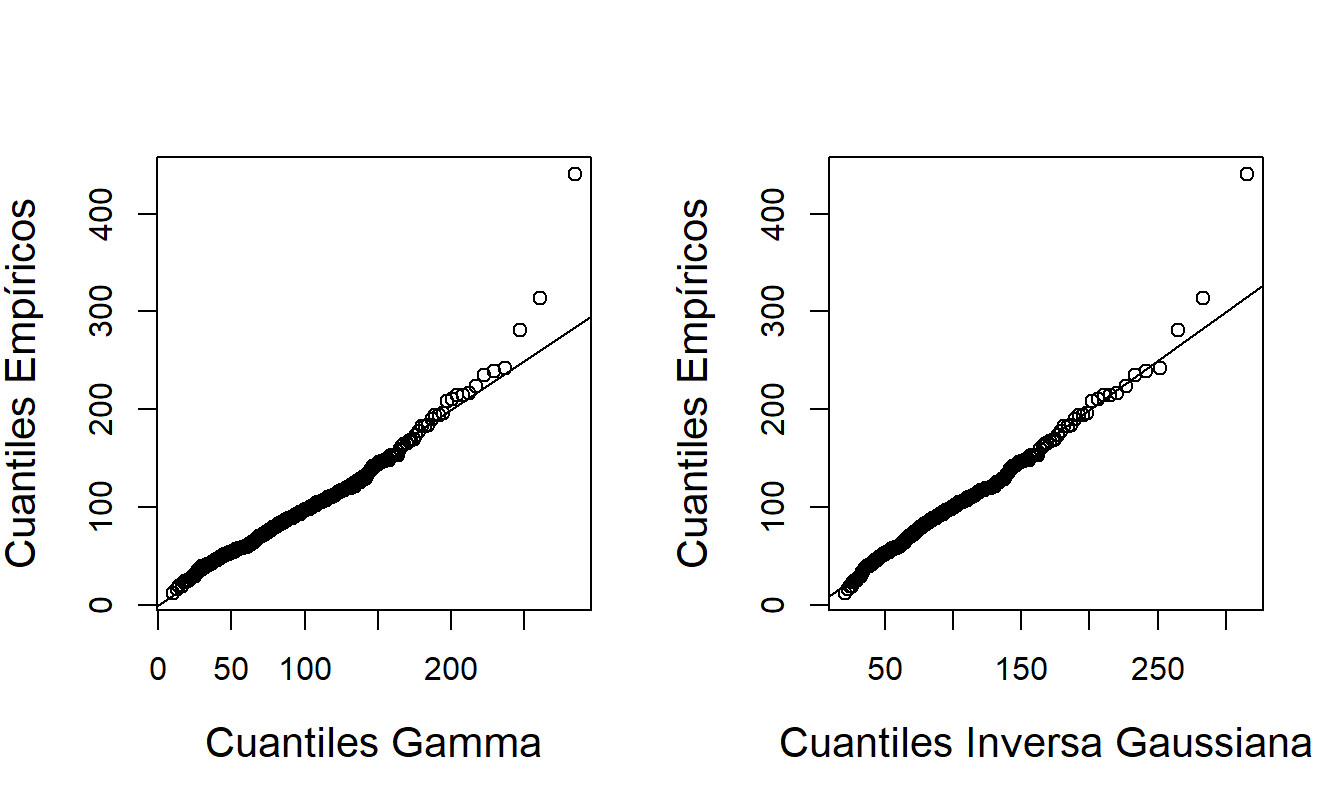
Gráficos \(qq\) de TPY para las distribuciones Gamma e Inversa Gaussiana

Figura 17.3: Gráficos \(qq\) de TPY para las distribuciones Gamma e Inversa Gaussiana

Código R para Producir Figura 17.3

Ajustamos los modelos lineales generalizados utilizando las distribuciones gamma e inversa gaussiana. En ambos modelos, elegimos la función de enlace logarítmica. El componente sistemático lineal común a cada modelo es \[\begin{eqnarray} && \eta = \beta_0 + \beta_1 \ln(\text{NumBed}) + \beta_2 \ln(\text{SqrFoot}) + \beta_3 \text{Pro} \\ && + \beta_4 \text{TaxExempt} + \beta_5 \text{SelfIns} + \beta_6 \text{MCert} + \beta_7 \text{Urban}. \notag \tag{17.1} \end{eqnarray}\]

Table 17.2 resume las estimaciones de los parámetros de los modelos. Al comparar las estadísticas BIC, o el AIC y el logaritmo de verosimilitud dado que el número de parámetros estimados y el tamaño de la muestra en ambos modelos son idénticos, encontramos que el modelo gamma se desempeña mejor que el inverso gaussiano. Como era de esperar, el coeficiente para la variable de tamaño NumBed es positivo y significativo. La única otra variable que es estadísticamente significativa es la variable SqrFoot, y esto solo en el modelo gamma.

Table 17.2. Modelos Lineales Generalizados Ajustados para Hogares de Ancianos

\[ \small{ \begin{array}{l|rr|rr} \hline\hline &\text{Gamma} & & \text{Inversa} & \text{Gaussiana} \\ \text{Variables} & \text{Estimación} & \textit{t}\text{-ratio} & \text{Estimación} & \textit{t}\text{-ratio}\\ \hline \text{Intercepto} & -0.159 & -3.75 & -0.196 & -4.42 \\ \text{ln(NumBed) } & 0.996 & 66.46 & 1.023 & 65.08 \\ \text{ln(SqrFoot)} & 0.026 & 2.07 & 0.003 & 0.19 \\ \text{SelfIns} & 0.006 & 0.75 & 0.003 & 0.27 \\ \text{MCert } & -0.008 & -0.55 & -0.008 & -0.57 \\ \text{Pro} & 0.004 & 0.29 & 0.007 & 0.36 \\ \text{TaxExempt} & 0.018 & 1.28 & 0.021 & 1.12 \\ \text{Urban} & -0.011 & -1.25 & -0.006 & -0.64 \\ \text{Escala} & 165.64& & 0.0112 \\ \hline \\ \hline \end{array} \\ \text{Estadísticas de Bondad de Ajuste} \\ \begin{array}{lrr} \hline \text{Log-Verosimilitud} & -1,131.24 & -1,218.15 \\ \text{AIC} &2,280.47 & 2,454.31\\ \text{BIC} & 2,315.17 & 2,489.00 \\ \hline\hline \end{array} } \]

La Figura 17.4 presenta los gráficos de residuos de desviación contra los valores ajustados de TPY para los modelos gamma e inversa gaussiana. No se encuentran patrones en los gráficos, lo que respalda la posición de que estos modelos son ajustes razonables para los datos.

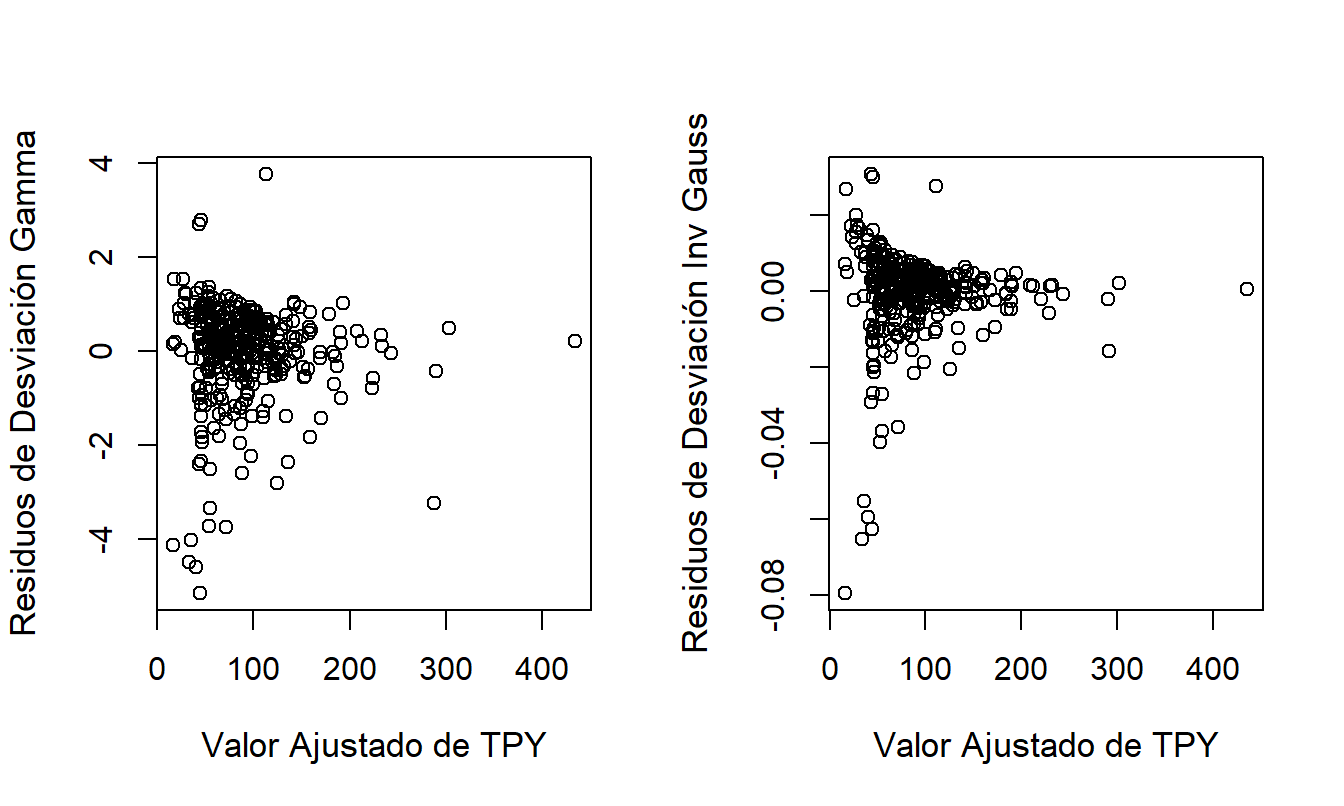
Gráficos de Residuos de Desviación versus Valores Ajustados para los Modelos Gamma e Inversa Gaussiana.

Figura 17.4: Gráficos de Residuos de Desviación versus Valores Ajustados para los Modelos Gamma e Inversa Gaussiana.

Código R para Producir Figura 17.4

17.4 Distribuciones Generalizadas

Otra forma de manejar datos de regresión con colas pesadas es usar distribuciones paramétricas, como las utilizadas en el modelado de supervivencia. Aunque el análisis de supervivencia se enfoca en datos censurados, los métodos pueden aplicarse perfectamente a datos completos. En la Sección 14.3 introdujimos un modelo de tiempo de falla acelerado (AFT). El AFT es un modelo logarítmico de ubicación-escala, de modo que \(\ln (y)\) sigue una distribución paramétrica de densidad de ubicación-escala en la forma \(\mathrm{f}(y)=\mathrm{f}_0\left( (y-\mu )/\sigma \right) /\sigma\), donde \(\mu\) y \(\sigma >0\) son los parámetros de ubicación y escala, y \(\mathrm{f}_0\) es la forma estándar de la distribución. Las distribuciones Weibull, lognormal y log-logística son distribuciones de tiempo de vida comúnmente usadas que son casos especiales del marco AFT.

Para ajustar distribuciones de cola pesada de interés en ciencias actuariales, consideramos la siguiente variación menor y examinamos distribuciones a partir de la relación \[\begin{equation} \ln y = \mu + \sigma \ln y_0. \tag{17.2} \end{equation}\] Como antes, la distribución asociada con \(y_0\) es una estándar y nos interesa la distribución de la variable aleatoria \(y\). Dos casos especiales importantes son la gamma generalizada y la beta generalizada del segundo tipo. Estas distribuciones se han utilizado extensamente en el modelado de datos de seguros, véase, por ejemplo, Klugman et al. (2008), aunque la mayoría de las aplicaciones no han utilizado covariables de regresión.

La distribución gamma generalizada se obtiene cuando \(y_0\) tiene una distribución gamma con parámetro de forma \(\alpha\) y parámetro de escala 1. Al incluir distribuciones límite (como permitir que los coeficientes se vuelvan arbitrariamente grandes), incluye las distribuciones exponencial, Weibull, gamma y lognormal como casos especiales. Por lo tanto, puede usarse para discriminar entre modelos alternativos. La distribución gamma generalizada también se conoce como la distribución gamma transformada (Klugman et al., 2008).

Cuando \(y_0\) tiene una distribución que es la razón de dos gammas, entonces \(y\) se dice que tiene una distribución beta generalizada del segundo tipo, comúnmente conocida por el acrónimo GB2. Específicamente, asumimos que \(y_0 = Gamma_1/Gamma_2\), donde \(Gamma_i\) tiene una distribución gamma con parámetro de forma \(\alpha_i\) y parámetro de escala 1, \(i=1,2\), y que \(Gamma_1\) y \(Gamma_2\) son independientes. Así, la familia GB2 tiene cuatro parámetros (\(\alpha_1\), \(\alpha_2\), \(\mu\) y \(\sigma\)) en comparación con los tres parámetros de la distribución gamma generalizada. Al incluir distribuciones límite, la GB2 abarca la gamma generalizada (permitiendo que \(\alpha_2 \rightarrow \infty\)) y, por ende, la exponencial, Weibull, y así sucesivamente. También abarca la Burr Tipo 12 (permitiendo que \(\alpha_1 = 1\)), así como otras familias de interés, incluidas las distribuciones de Pareto.

La distribución de \(y\) de la ecuación (17.2) contiene el parámetro de ubicación \(\mu\), el parámetro de escala \(\sigma\) y parámetros adicionales que describen la distribución de \(y_0\). En principio, se podría permitir que cualquier parámetro de la distribución sea una función de las covariables. Sin embargo, seguir este principio llevaría a un gran número de parámetros; esto típicamente genera dificultades computacionales así como problemas de interpretación. Para limitar el número de parámetros, es habitual asumir que los parámetros de \(y_0\) no dependen de las covariables. Es natural permitir que el parámetro de ubicación sea una función lineal de las covariables, de modo que \(\mu =\mu \left( \mathbf{x}\right)= \mathbf{x}^{\prime } \boldsymbol \beta\). También se puede permitir que el parámetro de escala \(\sigma\) dependa de \(\mathbf{x}\). Para \(\sigma\) positivo, una especificación común es \(\sigma =\sigma (\mathbf{x})\) \(= \exp(\mathbf{x}^{\prime }\boldsymbol \beta_{\sigma })\), donde \(\boldsymbol \beta_{\sigma}\) son coeficientes de regresión asociados con el parámetro de escala. Los demás parámetros suelen mantenerse fijos.

La interpretabilidad de los parámetros es una razón para mantener fijos el parámetro de escala y otros parámetros no relacionados con la ubicación. Al hacer esto, es sencillo demostrar que la función de regresión tiene la forma \[ \mathrm{E}\left( y|\mathbf{x}\right) =C\exp \left( \mu \left( \mathbf{x} \right) \right) =C~e^{\mathbf{x}^{\prime }\boldsymbol \beta}, \] donde la constante \(C\) es una función de otros parámetros del modelo (no relacionados con la ubicación). Así, se pueden interpretar los coeficientes de regresión en términos de un cambio proporcional (una elasticidad en economía). Es decir, \(\partial \left[ \ln \mathrm{E}(y) \right] /\partial x_k= \beta_k.\)

Otra razón para mantener fijos los parámetros no relacionados con la ubicación es la facilidad de calcular residuos razonables y usar estos residuos para ayudar con la selección del modelo. Específicamente, con la ecuación (17.2), se pueden calcular residuos de la forma \[ r_i = \frac{\ln y_i-\widehat{\mu}_i }{\widehat{\sigma }}, \] donde \(\widehat{\mu}_i\) y \(\widehat{\sigma }\) son estimaciones de máxima verosimilitud. Para conjuntos de datos grandes, podemos asumir poco error de estimación, de modo que \(r_i \approx (\ln y_i - \mu_i) /\sigma,\) y la cantidad en el lado derecho tiene una distribución conocida.

Para ilustrar, considere el caso en que \(y\) sigue una distribución GB2. En este caso, \[ y_0 = \frac{Gamma_1}{Gamma_2}= \frac{\alpha_1}{\alpha_2} \times \frac{Gamma_1/(2\alpha_1)}{Gamma_2/(2\alpha_2)} = \frac{\alpha_1}{\alpha_2} \times F , \] donde \(F\) tiene una distribución \(F\) con grados de libertad del numerador y denominador \(df_1 = 2 \alpha_1\) y \(df_2 = 2 \alpha_2\). Entonces, \(\exp(r_i) \approx (\alpha_1 /\alpha_2) F_i\), de modo que los residuos exponenciados deberían tener una distribución aproximada F (hasta un parámetro de escala). Este hecho permite calcular gráficos cuantiles-cuantiles (qq) para evaluar gráficamente la adecuación del modelo.

Para ilustrar, consideramos algunos ejemplos relacionados con seguros que utilizan modelos de regresión con colas pesadas. McDonald y Butler (1990) discutieron modelos de regresión que incluyen los comúnmente usados, así como las distribuciones GB2 y gamma generalizada. Aplicaron el modelo a la duración de períodos de pobreza y encontraron que la GB2 mejoraba significativamente el ajuste del modelo sobre la lognormal. Beirlant et al. (1998) propusieron dos modelos de regresión Burr y los aplicaron a la segmentación de carteras para seguros contra incendios. La Burr es una extensión de la distribución de Pareto, aunque sigue siendo un caso especial de la GB2. Manning, Basu y Mullahy (2005) aplicaron la distribución gamma generalizada a los gastos hospitalarios usando datos de un estudio de hospitales realizado en la Universidad de Chicago.

Debido a que el modelo de regresión es completamente paramétrico, la máxima verosimilitud es generalmente el método de estimación preferido. Si \(y\) sigue una distribución GB2, cálculos sencillos muestran que su densidad puede expresarse como \[\begin{equation} f(y; \mu, \sigma, \alpha_1, \alpha_2) = \frac{[\exp( z)]^{\alpha_{1}}}{y |\sigma| B(\alpha_1, \alpha_2) [1 + \exp(z) ]^{\alpha_1 + \alpha_2} }, \tag{17.3} \end{equation}\] donde \(z= (\ln y - \mu)/{\sigma}\) y B(\(\cdot,\cdot\)) es la función beta, definida como \(\text{B}(\alpha_1, \alpha_2) = \Gamma(\alpha_1)\Gamma(\alpha_2)/\Gamma(\alpha_1+\alpha_2)\). Esta densidad puede usarse directamente en rutinas de verosimilitud de muchos paquetes estadísticos. Como se describe en la Sección 11.9, el método de máxima verosimilitud proporciona automáticamente:

  • errores estándar para las estimaciones de los parámetros,
  • métodos de selección de modelos mediante pruebas de razón de verosimilitudes y
  • estadísticas de bondad de ajuste como AIC y BIC.

Aplicación: Hogares de Ancianos en Wisconsin

En los modelos lineales generalizados ajustados resumidos en la Tabla Tabla 17.2, vimos que los coeficientes asociados con ln(NumBed) estaban cerca de uno. Esto sugiere identificar ln(NumBed) como una variable de desplazamiento, es decir, forzar que el coeficiente asociado con ln(NumBed) sea 1. Para otra estrategia de modelado, también sugiere reescalar la variable dependiente por NumBed. Esto es razonable porque usamos una función de enlace logarítmica, de modo que el valor esperado de TPY es proporcional a NumBed. Siguiendo este enfoque, ahora definimos la tasa de ocupación anual (Rate) como \[\begin{equation} \text{Tasa de Ocupación} = \frac{\text{Días Totales de Pacientes}}{\text{Número de Camas} \times \text{Días Abierto}} \times 100. \tag{17.4} \end{equation}\] Esta nueva variable dependiente es fácil de interpretar: mide el porcentaje de camas ocupadas en un día cualquiera. Las tasas de ocupación se calcularon usando el número promedio de camas licenciadas dentro de un año de reporte de costos en lugar del número de camas licenciadas en un día específico. Esto da lugar a algunas tasas de ocupación mayores al 100.

Una dificultad de usar tasas de ocupación es que su distribución no puede aproximarse razonablemente por un miembro de la familia exponencial. La Figura 17.5 muestra un histograma suavizado de la variable Rate (usando un suavizador de núcleo); esta distribución está sesgada a la izquierda. Superpuesta con la línea discontinua está la distribución inversa gaussiana donde los parámetros se ajustaron sin covariables, usando el método de momentos. Las distribuciones gamma y normal están muy cerca de la inversa gaussiana, y por lo tanto no se muestran aquí. En contraste, la distribución GB2 ajustada (también sin covariables) mostrada en la Figura 17.5 captura partes importantes de la distribución; en particular, captura la agudeza y el sesgo hacia la izquierda.

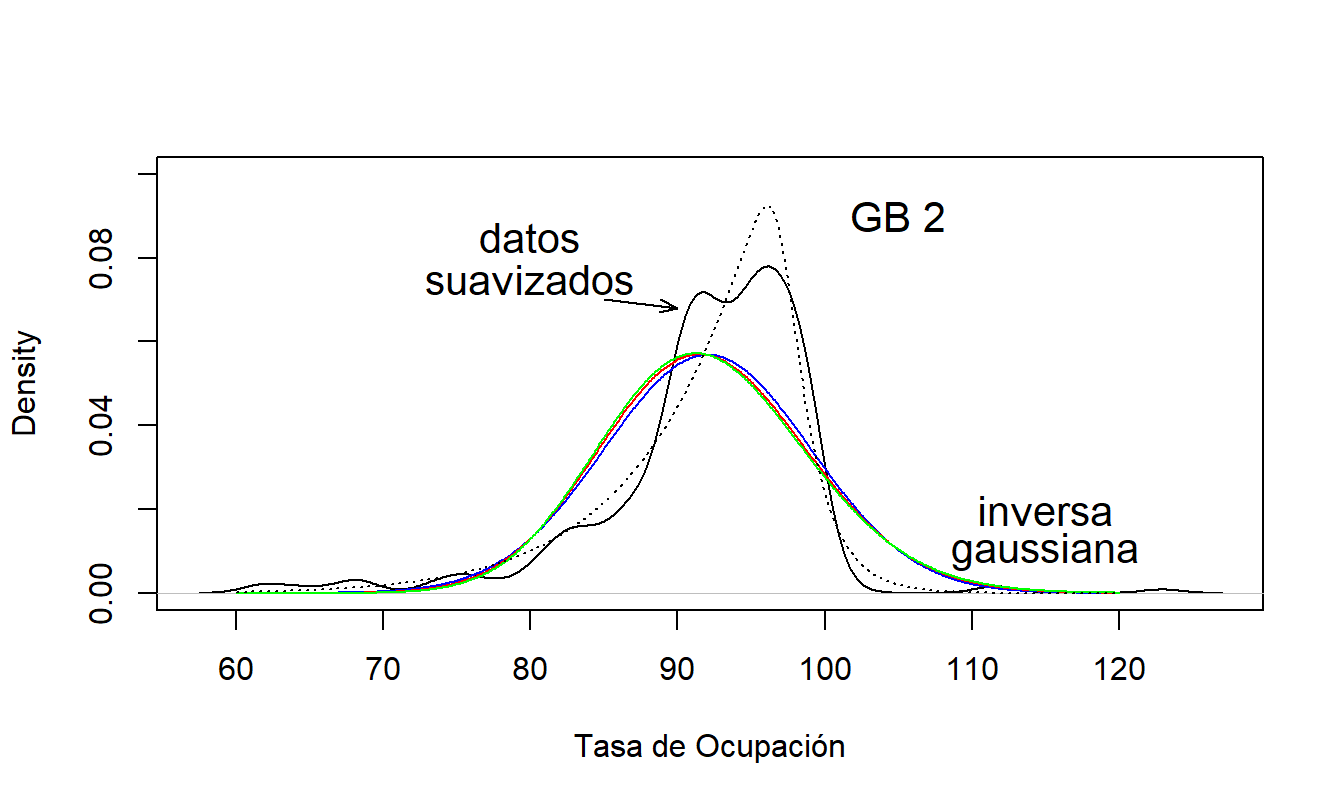
Densidades de Hogares de Ancianos. La versión empírica, basada en una estimación de densidad por núcleo, se compara con densidades ajustadas de GB2 e inversa gaussiana.

Figura 17.5: Densidades de Hogares de Ancianos. La versión empírica, basada en una estimación de densidad por núcleo, se compara con densidades ajustadas de GB2 e inversa gaussiana.

Código R para producir la Figura 17.5

La distribución GB2 se ajustó utilizando máxima verosimilitud con las mismas covariables que en la Tabla 17.2. Específicamente, utilizamos el parámetro de ubicación \(\mu = \exp(\eta)\), donde \(\eta\) se especifica en la ecuación (17.1). Como es habitual en la estimación por verosimilitud, reparametrizamos la escala y los dos parámetros de forma, \(\sigma\), \(\alpha_1\) y \(\alpha_2\), para ser transformados en la escala logarítmica, de modo que pudieran abarcar toda la línea real. De esta manera, evitamos problemas de límites que podrían surgir al intentar ajustar modelos con valores negativos de parámetros. La Tabla 17.3 resume el modelo ajustado. Desafortunadamente, para este modelo ajustado, ninguna de las variables explicativas resultó estadísticamente significativa. (Recordemos que reescalamos por número de camas, una variable explicativa muy importante.)

Tabla 17.3. Modelos Generalizados de Hogares de Ancianos en Wisconsin

\[ \small{ \begin{array}{l|rr|rr} \hline \hline \hline & \text{Gamma }& \text{Generalizada} &\text{GB2} \\ \hline \text{Variables} & \text{Estimación} & \textit{t}\text{-ratio} &\text{Estimación} & \textit{t}\text{-ratio} \\ \hline \text{Intercepto} & 4.522 & 78.15 & 4.584 & 198.47 \\ \text{ln(NumBed)} & -0.027 & -2.06 & -0.010 & -1.17 \\ \text{ln(SqrFoot)} & 0.031 & 2.89 & 0.010 & 1.28 \\ \text{SelfIns} & 0.003 & 0.44 & -0.001 & -0.25 \\ \text{MCert} & -0.010 & -0.81 & -0.010 & -1.30 \\ \text{Pro } & -0.021 & -1.46 & -0.002 & -0.20 \\ \text{TaxExempt} & -0.007 & -0.48 & 0.015 & 1.66 \\ \text{Urbano} & -0.014 & -1.78 & -0.003 & -0.60 \\ \hline & \text{Estimación} &\text{Error Estándar} & \text{Estimación} & \text{Error Estándar} \\ \ln \sigma & -2.406 & 0.131 & -5.553 & 1.716 \\ \ln \alpha_1 & 0.655 & 0.236 & -2.906 & 1.752 \\ \ln \alpha_2 & & & -1.696 & 1.750 \\ \end{array} \\ \begin{array}{l|rr} \hline \text{Log-Verosimilitud} &-1,148.135 & -1,098.723 \\ \text{AIC} & 2,316.270 & 2,219.446 \\ \text{BIC} & 2,319.296 & 2,223.822\\ \hline\hline \end{array} } \]

Para evaluar más el ajuste del modelo, la Figura 17.6 muestra los residuos de este modelo ajustado. Para estas figuras, los residuos se calculan usando \(r_i = (\ln y_i-\widehat{\mu}_i)/\widehat{\sigma }.\) El panel izquierdo muestra los residuos frente a los valores ajustados (\(\exp(\widehat{\mu}_i)\)); no se evidencian patrones aparentes en esta visualización. El panel derecho es un gráfico \(qq\) de residuos, donde las distribuciones de referencia es la distribución \(F\) logarítmica (más una constante) descrita anteriormente. Esta figura muestra algunas discrepancias para valores más pequeños de hogares de ancianos. Debido a esto, la Tabla 17.3 también informa ajustes del modelo gamma generalizado. Este ajuste es más satisfactorio en el sentido de que dos de las variables explicativas son estadísticamente significativas. Sin embargo, a partir de las estadísticas de bondad de ajuste, vemos que la GB2 es un modelo mejor ajustado. Cabe señalar que las estadísticas de bondad de ajuste para el modelo gamma generalizado no son directamente comparables con los ajustes de regresión gamma en la Tabla 17.2; esto se debe únicamente a que la variable dependiente difiere por la variable de escala NumBeds.

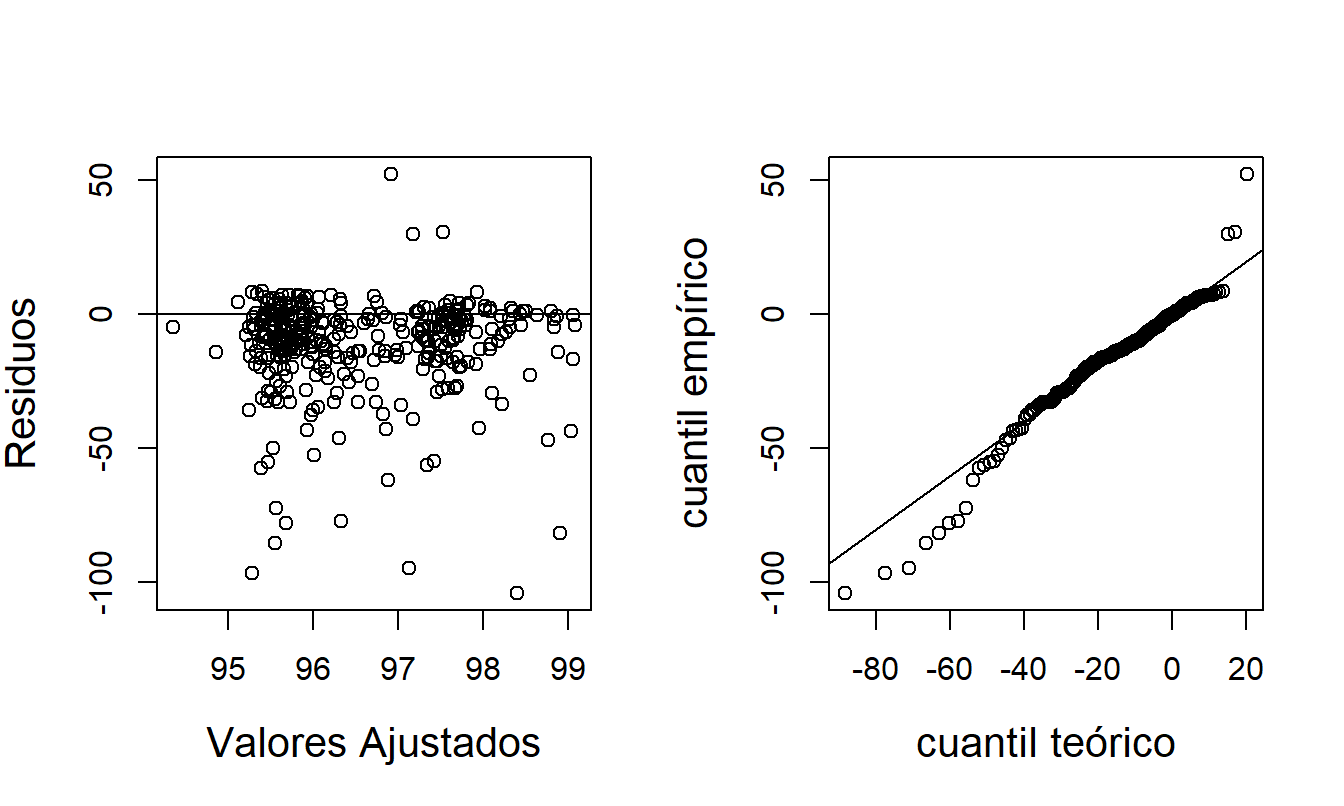
Análisis de Residuos del Modelo GB2. El panel izquierdo es un gráfico de residuos frente a valores ajustados. El panel derecho es un gráfico \(qq\) de residuos.

Figura 17.6: Análisis de Residuos del Modelo GB2. El panel izquierdo es un gráfico de residuos frente a valores ajustados. El panel derecho es un gráfico \(qq\) de residuos.

Código R para producir la Figura 17.6

17.5 Regresión por Cuantiles

La regresión por cuantiles es una extensión de la regresión por la mediana, por lo que es útil introducir este concepto primero.

En la regresión por la mediana, se encuentra el conjunto de coeficientes de regresión \(\boldsymbol \beta\) que minimiza

\[ \sum_{i=1}^n | y_i - \mathbf{x}_i^{\prime} \boldsymbol \beta |. \] Es decir, simplemente reemplazamos la función de pérdida cuadrática habitual por una función de valor absoluto. Aunque no entraremos en detalles aquí, encontrar estos coeficientes óptimos es un problema de optimización simple en programación no lineal que puede implementarse fácilmente en software estadístico moderno.

Debido a que este procedimiento utiliza el valor absoluto como función de pérdida, la regresión por la mediana también se conoce como LAD por mínima desviación absoluta en comparación con OLS (mínimos cuadrados ordinarios). El adjetivo “mediana” proviene del caso especial en el que no hay regresores, de modo que \(\mathbf{x}\) es un escalar igual a 1. En este caso, el problema de minimización se reduce a encontrar un intercepto \(\beta_0\) que minimice

\[ \sum_{i=1}^n | y_i - \beta_0 |. \] La solución a este problema es la mediana de \(\{y_1, \ldots, y_n\}\).

Supongamos que también desea encontrar el percentil \(25^{\rm th}\), \(75^{\rm th}\), o algún otro percentil de \(\{y_1, \ldots, y_n\}\). También se puede usar este procedimiento de optimización para encontrar cualquier percentil, o cuantil. Sea \(\tau\) una fracción entre 0 y 1. Entonces, el cuantil \(\tau^{\rm th}\) de la muestra \(\{y_1, \ldots, y_n\}\) es el valor de \(\beta_0\) que minimiza \[ \sum_{i=1}^n \rho_{\tau}( y_i - \beta_0). \] Aquí, \(\rho_{\tau}(u)=u(\tau-{\rm I}(u\leq0))\) se llama una función de chequeo y \({\rm I}(\cdot)\) es la función indicadora.

Extendiendo este procedimiento, en la regresión por cuantiles se encuentra el conjunto de coeficientes de regresión \(\boldsymbol \beta\) que minimiza \[ \sum_{i=1}^n \rho_{\tau}( y_i - \mathbf{x}_i^{\prime} \boldsymbol \beta ). \] Los coeficientes de regresión estimados dependen de la fracción \(\tau\), por lo que usamos la notación \(\widehat{\boldsymbol \beta}(\tau)\) para enfatizar esta dependencia. La cantidad \(\mathbf{x}_i^{\prime}\widehat{\boldsymbol \beta}(\tau)\) representa el cuantil \(\tau^{\rm th}\) de la distribución de \(y_i\) para el vector explicativo \(\mathbf{x}_i\). Para ilustrar, para \(\tau = 0.5\), \(\mathbf{x}_i^{\prime}\widehat{\boldsymbol \beta}(0.5)\) representa la mediana estimada de la distribución de \(y_i\). En contraste, el valor ajustado por \(OLS\) \(\mathbf{x}_i^{\prime}\mathbf{b}\) representa la media estimada de la distribución de \(y_i\).

Ejemplo: Hogares de Ancianos en Wisconsin - Continuación. Para ilustrar las técnicas de regresión por cuantiles, ajustamos una regresión del metraje cuadrado (SqrFoot) sobre los años totales de personas (TPY). La Figura 17.7 muestra la relación entre estas dos variables, con líneas ajustadas de media (OLS) y mediana (LAD) superpuestas. A diferencia de la distribución original de TPY que está sesgada, para cada valor de SqrFoot podemos ver poca diferencia entre los valores de media y mediana. Esto sugiere que la distribución condicional de TPY dado SqrFoot no está sesgada.

La Figura 17.7 también muestra las líneas ajustadas que resultan de ajustar regresiones por cuantiles en cuatro valores adicionales de \(\tau =0.05,0.25, 0.75\) y 0.95. Estos ajustes están indicados por las líneas grises. Para cada valor de SqrFoot, visualmente podemos tener una idea de los percentiles \(5^{\rm th}\), \(25^{\rm th}\), \(50^{\rm th}\), \(75^{\rm th}\) y \(95^{\rm th}\) de la distribución de TPY. Aunque los mínimos cuadrados ordinarios clásicos también proporcionan esto, las recetas clásicas generalmente asumen homocedasticidad. A partir de 17.7, vemos que la distribución de \(y\) parece ensancharse a medida que SqrFoot aumenta, lo que sugiere una relación heterocedástica.

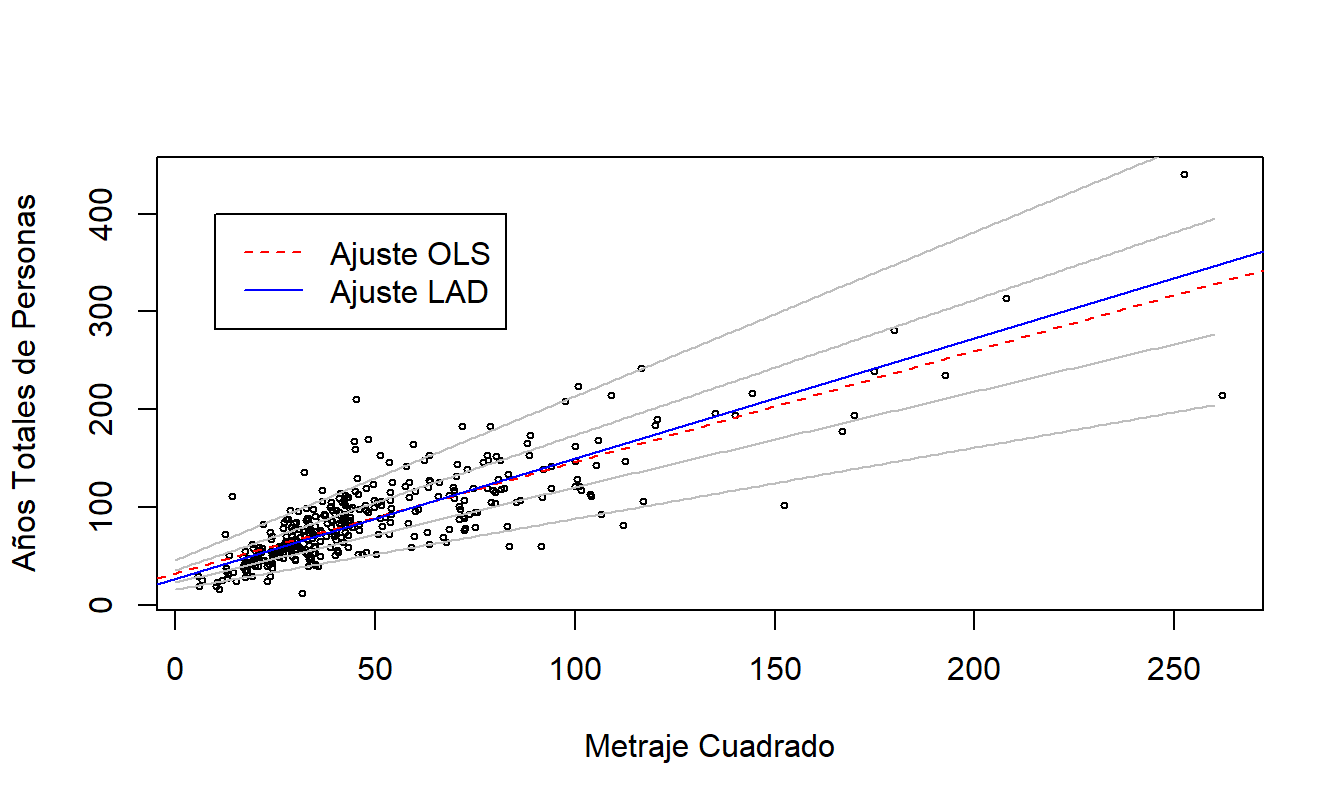
Ajustes de Regresión por Cuantiles del Metraje Cuadrado sobre los Años Totales de Personas. Se superponen los ajustes de las regresiones de media (OLS) y mediana (LAD), indicados en la leyenda. También se superponen, con líneas grises, los ajustes de regresión por cuantiles – de abajo hacia arriba, los ajustes corresponden a \(\tau =0.05,0.25, 0.75\) y 0.95.

Figura 17.7: Ajustes de Regresión por Cuantiles del Metraje Cuadrado sobre los Años Totales de Personas. Se superponen los ajustes de las regresiones de media (OLS) y mediana (LAD), indicados en la leyenda. También se superponen, con líneas grises, los ajustes de regresión por cuantiles – de abajo hacia arriba, los ajustes corresponden a \(\tau =0.05,0.25, 0.75\) y 0.95.

Código R para producir la Figura 17.7

Las regresiones por cuantiles funcionan bien en situaciones donde los mínimos cuadrados ordinarios requieren atención cuidadosa para usarse con confianza. Como se demostró en el ejemplo de Hogares de Ancianos en Wisconsin, la regresión por cuantiles maneja fácilmente distribuciones sesgadas y heterocedasticidad. Así como los cuantiles ordinarios son relativamente robustos a observaciones inusuales, las estimaciones de la regresión por cuantiles son mucho menos sensibles a observaciones atípicas que las rutinas de regresión habituales.

17.6 Modelos de Valores Extremos

Los modelos de valores extremos se enfocan en los extremos, la “punta del iceberg,” como la temperatura más alta en un mes, el tiempo más rápido para correr un kilómetro o el menor rendimiento del mercado de valores. Algunos modelos de valores extremos están motivados por estadísticas máximas. Supongamos que consideramos la compensación anual de los directores ejecutivos (CEO) en un país, \(y_1, y_2, \ldots\). Entonces, \(M = \max(y_1, \ldots, y_n)\) representa la compensación del CEO mejor pagado durante el año. Si los valores \(y\) fueran observados, podríamos usar algunos supuestos adicionales leves (como independencia) para hacer inferencias sobre la distribución de \(M\). Sin embargo, en muchos casos, solo se observa \(M\) directamente, lo que nos obliga a basar los procedimientos de inferencia en observaciones “extremas” \(M\). Como variación, podríamos tener observaciones de los 20 principales CEO, no de toda la población. Esta variación utiliza inferencia basada en las “20” estadísticas de orden más grandes, véase por ejemplo Coles (2003, Sección 3.5.2).

El modelado de \(M\) a menudo se basa en la distribución generalizada de valores extremos, o \(GEV\), definida por la función de distribución \[\begin{equation} \Pr(M \leq x) = \exp \left[-(1+ \gamma z )^{-1/\gamma} \right], \tag{17.5} \end{equation}\] donde \(z=(x-\mu)/ \sigma\). Este es un modelo de ubicación-escala, con parámetros de ubicación y escala \(\mu\) y \(\sigma\), respectivamente. En el caso estándar donde \(\mu=0\) y \(\sigma=1\), permitiendo \(\gamma \rightarrow \infty\) significa que \(\Pr(M \leq x) \rightarrow \exp \left[- e^{-x} \right],\) la distribución clásica de valores extremos. Por lo tanto, el parámetro \(\gamma\) proporciona la generalización de esta distribución clásica.

Beirlant, Goegebeur, Segers y Teugels (2004) discuten formas en que se podrían introducir covariables de regresión en la distribución \(GEV\), esencialmente permitiendo que cada parámetro dependa de las covariables. La estimación se realiza mediante máxima verosimilitud. En sus procedimientos de inferencia, el enfoque está en el comportamiento de los cuantiles extremos (condicionales a las covariables).

Otro enfoque para modelar valores extremos es centrarse en datos que deben ser grandes para ser incluidos en la muestra.

Ejemplo: Grandes Reclamos Médicos. Cebrián, Denuit y Lambert (2003) analizaron 75,789 grandes reclamos de seguros médicos grupales de 1991. Para ser incluidos en esta base de datos, los reclamos debían superar los 25,000. Por lo tanto, estos datos están truncados a la izquierda en 25,000. El interés en su estudio fue interpretar la distribución de cola larga en términos de las covariables edad y sexo.

El enfoque de picos sobre el umbral para modelar valores extremos está motivado por datos truncados a la izquierda donde el punto de truncamiento, o “umbral,” es grande. Para ser incluidos en el conjunto de datos, las observaciones deben superar un umbral grande al que nos referimos como un “pico.” Siguiendo nuestra discusión en la Sección 14.2 sobre truncamiento, si \(C_L\) es el punto de truncamiento a la izquierda, entonces la función de distribución de \(y-C_L\) dado que \(y>C_L\) es \(1 - \Pr(y-C_L > x |y>C_L)\) \(= 1 - (1-F_y(C_L+x))/(1-F_y(C_L))\). En lugar de modelar directamente la distribución de \(y\), \(F_y\), como en secciones anteriores, se asume que puede aproximarse directamente mediante una distribución Pareto generalizada. Es decir, asumimos \[\begin{equation} \Pr(y-C_L \leq x |y>C_L) \approx 1 - (1+ \frac{z}{\theta} )^{-\theta} , \tag{17.6} \end{equation}\] donde \(z=x / \sigma\), \(\sigma\) es un parámetro de escala, \(x \geq 0\) si \(\theta \geq 0\) y \(0 \leq x \leq - \theta\) si \(\theta < 0\). Aquí, el lado derecho de la ecuación (17.6) es la distribución Pareto generalizada. La distribución Pareto usual restringe \(\theta\) a ser positivo; esta especificación permite valores negativos de \(\theta\). Permitir que \(\theta \rightarrow 0\) implica que \(1 - (1+ z/\theta )^{-\theta} \rightarrow 1 - e^{-x/\sigma},\) la distribución exponencial.

Ejemplo: Grandes Reclamos Médicos - Continuación. Para incorporar las covariables edad y sexo, Cebrián et al. (2003) categorizaron las variables, permitieron que los parámetros variaran por categoría y estimaron cada categoría de manera independiente. Alternativamente, enfoques más eficientes se describen en el Capítulo 7 de Beirlant et al. (2004).

17.7 Lecturas Adicionales y Referencias

La literatura sobre modelado de reclamos de cola larga está en constante desarrollo. Una referencia estándar es Klugman et al. (2008). Kleiber y Kotz (2003) ofrecen una excelente revisión de la literatura univariada, con muchas referencias históricas. Carroll y Ruppert (1988) proporcionan extensas discusiones sobre transformaciones en el modelado de regresión.

Este capítulo ha enfatizado la distribución GB2 con sus muchos casos especiales. Venter (2007) analiza extensiones del modelo lineal generalizado, enfocándose en aplicaciones de reserva de pérdidas. Balasooriya y Low (2008) presentan aplicaciones recientes al modelado de reclamos de seguros, aunque sin covariables de regresión. Otro enfoque es usar una distribución elíptica sesgada (como la normal o \(t\)-). Bali y Theodossiou (2008) presentan una aplicación reciente, mostrando cómo usar tales distribuciones en el modelado de series temporales de rendimientos de acciones.

Koenker (2005) es una excelente introducción extensa a la regresión por cuantiles. Yu, Lu y Stander (2003) ofrecen una introducción breve y accesible.

Coles (2003) y Beirlant et al. (2004) son dos excelentes introducciones extensas a las estadísticas de valores extremos.

Referencias del Capítulo

  • Balasooriya, Uditha and Chan-Kee Low (2008). Modeling insurance claims with extreme observations: Transformed kernel density and generalized lambda distribution. North American Actuarial Journal 11(2) 129-142.
  • Bali, Turan G. and Panayiotis Theodossiou (2008). Risk measurement of alternative distribution functions. Journal of Risk and Insurance 75(2), 411-437.
  • Beirlant, Jan, Yuir Goegebeur, Robert Verlaak and Petra Vynckier (1998). Burr regression and portfolio segmentation. Insurance: Mathematics and Economics 23, 231-250.
  • Beirlant, Jan, Yuir Goegebeur, Johan Segers and Jozef Teugels (2004). Statistics of Extremes. Wiley, New York.
  • Burbidge, J.B. and Magee, L. and Robb, A.L. (1988). Alternative transformations to handle extreme values of the dependent variable. Journal of the American Statistical Association 83, 123-127.
  • Carroll, Raymond and David Ruppert (1988). Transformation and Weighting in Regression. Chapman-Hall.
  • Cebrián, Ana C., Michel Denuit and Philippe Lambert (2003). Generalized Pareto fit to the Society of Actuaries’ large claims database. North American Actuarial Journal 7 (3), 18-36.
  • Coles, Stuart (2003). An Introduction to Statistical Modeling of Extreme Values. Springer, New York.
  • Cummins, J. David, Georges Dionne, James B. McDonald and B. Michael Pritchett (1990). Applications of the GB2 family of distributions in modeling insurance loss processes. Insurance: Mathematics and Economics 9, 257-272.
  • John, J. A. and Norman R. Draper (1980). An alternative family of transformations. Applied Statistics 29 (2), 190-197.
  • Kleiber, Christian and Samuel Kotz (2003). Statistical Size Distributions in Economics and Actuarial Sciences. John Wiley and Sons, New York.
  • Klugman, Stuart A, Harry H. Panjer and Gordon E. Willmot (2008). Loss Models: From Data to Decisions. John Wiley & Sons, Hoboken, New Jersey.
  • Koenker, Roger (2005). Quantile Regression. Cambridge University Press, New York.
  • Manning, William G (1998). The logged dependent variable, heteroscedasticity, and the retransformation problem. Journal of Health Economics 17, 283-295.
  • Manning, William G, Anirban Basu and John Mullahy (2005). Generalized modeling approaches to risk adjustment of skewed outcomes data. Journal of Health Economics 24, 465-488.
  • McDonald, James B. and Richard J. Butler (1990). Regression models for positive random variables. Journal of Econometrics 43, 227-251.
  • Rachev, Svetiozar, T., Christian Menn and Frank Fabozzi (2005). Fat-Tailed and Skewed Asset Return Distributions: Implications for Risk Management, Portfolio Selection, and Option Pricing. Wiley, New York.
  • Rosenberg, Marjorie A., Edward W. Frees, Jiafeng Sun, Paul Johnson and James M. Robinson (2007). Predictive modeling with longitudinal data: A case study of Wisconsin nursing homes. North American Actuarial Journal 11(3), 54-69.
  • Sun, Jiafeng, Edward W. Frees and Marjorie A. Rosenberg (2008). Heavy-tailed longitudinal data modeling using copulas. Insurance: Mathematics and Economics 42(2), 817-830.
  • Venter, Gary (2007). Generalized linear models beyond the exponential family with loss reserve applications. Astin Bulletin: Journal of the International Actuarial Association 37 (2), 345-364.
  • Yeo, In-Kwon and Richard A. Johnson (2000). A new family of power transformations to improve normality or symmetry. Biometrika 87, 954-959.
  • Yu, Keming, Zudi Lu and Julian Stander (2003). Quantile regression: applications and current research areas. Journal of the Royal Statistical Society Series D (The Statistician) 52 (3), 331-350.

17.8 Ejercicios

17.1. Cuantiles y Simulación. Use la ecuación (17.2) para establecer las siguientes relaciones distribucionales que son útiles para calcular cuantiles.

  1. Suponga que \(y_0 = \alpha_1 F/\alpha_2\) donde \(F\) tiene una distribución \(F\) con grados de libertad del numerador y denominador \(df_1 = 2 \alpha_1\) y \(df_2 = 2 \alpha_2\). Muestre que \(y\) tiene una distribución GB2.

  2. Suponga que \(y_0 = B/(1-B),\) donde \(B\) tiene una distribución beta con parámetros \(\alpha_1\) y \(\alpha_2\). Muestre que \(y\) tiene una distribución GB2.

  3. Describa cómo usar las partes (a) y (b) para calcular cuantiles.

  4. Describa cómo usar las partes (a) y (b) para simulación.

17.2 Considere una función de densidad de probabilidad GB2 dada en la ecuación (17.3).

  1. Reparametrize la distribución definiendo el nuevo parámetro \(\theta =e^{\mu }.\) Muestre que la densidad puede expresarse como: \[ \mathrm{f}_{GB2}(y;\theta, \sigma ,\alpha _1,\alpha _2)=\frac{\Gamma \left( \alpha _1+\alpha _2\right) }{\Gamma \left( \alpha _1\right) \Gamma \left( \alpha _2\right) }\frac{\left( y/\theta \right) ^{\alpha _2/\sigma }}{\sigma y\left[ 1+\left( y/\theta \right) ^{1/\sigma }\right] ^{\alpha _1+\alpha _2}}, \]

  2. Usando la parte (a), muestre que \[ \lim_{\alpha _2\rightarrow \infty }\mathrm{f}_{GB2}(y; \theta \alpha _2^{\sigma },\sigma ,\alpha _1,\alpha _2)=\frac{1}{\sigma y\Gamma \left( \alpha _1\right) }\left( y/\theta \right) ^{\alpha _1/\sigma }\exp \left( -\left( y/\theta \right) ^{1/\sigma }\right) =\mathrm{f}_{GG}(y;\theta, \sigma, \alpha _1), \] una densidad gamma generalizada.

  3. Usando la parte (a), muestre que \[ \mathrm{f}_{GB2}(y;\theta, \sigma, 1, \alpha_2)=\frac{\alpha _2\left( y/\theta \right) ^{\alpha _2/\sigma }}{\sigma y\left[ 1+\left( y/\theta \right) ^{1/\sigma }\right] ^{1+\alpha _2}}=\mathrm{f}_{Burr}(y;\theta, \sigma, \alpha _2), \] una densidad Burr Tipo 12.

17.3 Recuerde que la densidad de una distribución gamma con parámetro de forma \(\alpha\) y parámetro de escala \(\theta\) tiene una densidad dada por \(\mathrm{f}(y)=\left[ \theta ^{\alpha }\Gamma \left( \alpha \right) \right] ^{-1}y^{\alpha -1}\exp \left( -y/\theta \right)\) y el momento \(k\)-ésimo dado por \(\mathrm{E} (y^{k})=\theta ^{k}\Gamma \left( \alpha +k\right) /\Gamma \left( \alpha \right)\), para \(k>-\alpha.\)

  1. Para la distribución GB2, muestre que \[ \mathrm{E}(y)=e^{\mu }\frac{\Gamma \left( \alpha _1+\sigma \right) \Gamma \left( \alpha _2-\sigma \right) }{\Gamma \left( \alpha _1\right) \Gamma \left( \alpha _2\right) }. \]

  2. Para la distribución gamma generalizada, muestre que \[ \mathrm{E}(y)=e^{\mu }\Gamma \left( \alpha_1 +\sigma \right) /\Gamma \left( \alpha_1 \right) . \]

  3. Calcule los momentos de una densidad Burr Tipo 12.