Chapter 1 Regresión y la Distribución Normal

Vista Previa del Capítulo. El análisis de regresión es un método estadístico que se utiliza ampliamente en muchos campos de estudio, y la ciencia actuarial no es una excepción. Este capítulo proporciona una introducción al papel de la distribución normal en la regresión, el uso de transformaciones logarítmicas para especificar relaciones de regresión y la base de muestreo que es crítica para inferir resultados de regresión a poblaciones amplias de interés.

1.1 ¿Qué es el Análisis de Regresión?

La estadística trata sobre datos. Como disciplina, se ocupa de la recolección, resumen y análisis de datos para hacer afirmaciones sobre el mundo real. Cuando los analistas recolectan datos, realmente están recolectando información que se cuantifica, es decir, se transforma a una escala numérica. Existen reglas fáciles y bien entendidas para reducir los datos, utilizando medidas de resumen numéricas o gráficas. Estas medidas de resumen pueden luego vincularse a una representación teórica, o modelo, de los datos. Con un modelo que se calibra con datos, se pueden hacer afirmaciones sobre el mundo.

Los métodos estadísticos han tenido un gran impacto en varios campos de estudio.

  • En el área de recolección de datos, el diseño cuidadoso de encuestas por muestreo es crucial para los grupos de investigación de mercado y para los procedimientos de auditoría de las firmas de contabilidad.
  • El diseño experimental es una segunda subdisciplina dedicada a la recolección de datos. El enfoque del diseño experimental es construir métodos de recolección de datos que extraigan información de la manera más eficiente posible. Esto es especialmente importante en campos como la agricultura y la ingeniería, donde cada observación es costosa, posiblemente costando millones de dólares.
  • Otros métodos estadísticos aplicados se centran en la gestión y predicción de datos. El control de procesos se ocupa de monitorear un proceso a lo largo del tiempo y decidir cuándo la intervención es más fructífera. El control de procesos ayuda a gestionar la calidad de los bienes producidos por los fabricantes.
  • La previsión se trata de extrapolar un proceso hacia el futuro, ya sea las ventas de un producto o los movimientos de una tasa de interés.

El análisis de regresión es un método estadístico utilizado para analizar datos. Como veremos, la característica distintiva de este método es la capacidad de hacer afirmaciones sobre variables después de haber controlado los valores de variables explicativas conocidas. Aunque otros métodos son importantes, el análisis de regresión ha sido el más influyente. Para ilustrar, un índice de revistas de negocios, ABI/INFORM, enumera más de veinticuatro mil artículos que utilizan técnicas de regresión en el período de treinta años de 1978-2007. ¡Y estas son solo las aplicaciones que se consideraron lo suficientemente innovadoras como para ser publicadas en revistas académicas!

El análisis de regresión de datos es tan omnipresente en los negocios modernos que es fácil pasar por alto el hecho de que la metodología tiene poco más de 120 años. Los estudiosos atribuyen el nacimiento de la regresión al discurso presidencial de 1885 de Sir Francis Galton en la sección antropológica de la Asociación Británica para el Avance de las Ciencias. En ese discurso, descrito en Stigler (1986), Galton proporcionó una descripción de la regresión y la vinculó a la teoría de la curva normal. Su descubrimiento surgió de sus estudios sobre las propiedades de la selección natural y la herencia.

Para ilustrar un conjunto de datos que se puede analizar utilizando métodos de regresión, la Tabla 1.1 muestra algunos datos incluidos en el artículo de Galton de 1885. Esta tabla muestra las alturas de 928 hijos adultos, clasificados por un índice de la altura de sus padres. Aquí, todas las alturas femeninas se multiplicaron por 1.08, y el índice se creó tomando el promedio de la altura del padre y la altura reescalada de la madre. Galton era consciente de que tanto la altura de los padres como la del hijo adulto podían ser adecuadamente aproximadas por una curva normal. Al desarrollar el análisis de regresión, proporcionó un único modelo para la distribución conjunta de alturas.

Tabla 1.1: Galtons 1885 Regression Data
<64.0 64.5 65.5 66.5 67.5 68.5 69.5 70.5 71.5 72.5 >73.0 Total
>73.7 0 0 0 0 0 0 5 3 2 4 0 14
73.2 0 0 0 0 0 3 4 3 2 2 3 17
72.2 0 0 1 0 4 4 11 4 9 7 1 41
71.2 0 0 2 0 11 18 20 7 4 2 0 64
70.2 0 0 5 4 19 21 25 14 10 1 0 99
69.2 1 2 7 13 38 48 33 18 5 2 0 167
68.2 1 0 7 14 28 34 20 12 3 1 0 120
67.2 2 5 11 17 38 31 27 3 4 0 0 138
66.2 2 5 11 17 36 25 17 1 3 0 0 117
65.2 1 1 7 2 15 16 4 1 1 0 0 48
64.2 4 4 5 5 14 11 16 0 0 0 0 59
63.2 2 4 9 3 5 7 1 1 0 0 0 32
62.2 0 1 0 3 3 0 0 0 0 0 0 7
<61.2 1 1 1 0 0 1 0 1 0 0 0 5
Total 14 23 66 78 211 219 183 68 43 19 4 928

Fuente: Stigler (1986)

La Tabla 1.1 muestra que gran parte de la información sobre la altura de un hijo adulto puede atribuirse o ‘explicarse’ en términos de la altura de los padres. Por lo tanto, utilizamos el término variable explicativa para las mediciones que proporcionan información sobre una variable de interés. El análisis de regresión es un método para cuantificar la relación entre una variable de interés y las variables explicativas. La metodología utilizada para estudiar los datos en la Tabla 1.1 también se puede utilizar para estudiar problemas actuariales y de gestión de riesgos, la tesis de este libro.

1.2 Ajuste de Datos a una Distribución Normal

Históricamente, la distribución normal tuvo un papel fundamental en el desarrollo del análisis de regresión. Continúa desempeñando un papel importante, aunque estaremos interesados en extender las ideas de regresión a datos altamente ‘no normales’.

Formalmente, la curva normal se define por la función \[\begin{equation} \mathrm{f}(y)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left( -\frac{1}{2\sigma ^{2}% }\left( y-\mu \right) ^{2}\right) . \tag{1.1} \end{equation}\]

Esta curva es una función de densidad de probabilidad con toda la línea real como su dominio. De la ecuación (1.1), vemos que la curva es simétrica respecto a \(\mu\) (la media y la mediana). El grado de agudeza está controlado por el parámetro \(\sigma ^{2}\). Estos dos parámetros, \(\mu\) y \(\sigma ^{2}\), son conocidos como los parámetros de ubicación y escala, respectivamente. El Apéndice A3.1 proporciona detalles adicionales sobre esta curva, incluyendo un gráfico y tablas de su distribución acumulada que utilizaremos a lo largo del texto.

La curva normal también se muestra en la Figura 1.1, una imagen de un billete de moneda alemana ahora fuera de circulación, el diez Deutsche Mark. Este billete contiene la imagen del alemán Carl Gauss, un eminente matemático cuyo nombre a menudo se asocia con la curva normal (a veces se refiere a ella como la curva Gaussiana). Gauss desarrolló la curva normal en relación con la teoría de los mínimos cuadrados para ajustar curvas a los datos en 1809, aproximadamente al mismo tiempo que el trabajo relacionado del científico francés Pierre LaPlace. Según Stigler (1986), ¡hubo bastante acritud entre estos dos científicos sobre la prioridad del descubrimiento! La curva normal se utilizó por primera vez como una aproximación a los histogramas de datos alrededor de 1835 por Adolph Quetelet, un matemático y científico social belga. Como muchas cosas buenas, la curva normal ha existido durante algún tiempo, desde aproximadamente 1720 cuando Abraham de Moivre la derivó para su trabajo sobre modelado de juegos de azar. La curva normal es popular porque es fácil de usar y ha demostrado ser exitosa en muchas aplicaciones.

Diez Deutsche Mark. Moneda alemana con el científico Gauss y la curva normal.

Figura 1.1: Diez Deutsche Mark. Moneda alemana con el científico Gauss y la curva normal.

Ejemplo: Reclamaciones por Lesiones Corporales en Massachusetts. Para nuestra primera mirada al ajuste de la curva normal a un conjunto de datos, consideramos los datos de Rempala y Derrig (2005). Ellos consideraron las reclamaciones derivadas de coberturas de seguros de lesiones corporales por accidentes de automóvil. Estos son montos incurridos por tratamientos médicos ambulatorios que surgen de accidentes de automóvil, típicamente esguinces, fracturas de clavícula y similares. Los datos consisten en una muestra de 272 reclamaciones de Massachusetts que se cerraron en 2001 (por ‘cerradas,’ queremos decir que la reclamación está resuelta y no pueden surgir responsabilidades adicionales del mismo accidente). Rempala y Derrig estaban interesados en desarrollar procedimientos para manejar mezclas de reclamaciones ‘típicas’ y otras de proveedores que informaron reclamaciones fraudulentas. Para esta muestra, consideramos solo esas reclamaciones típicas, ignorando las potencialmente fraudulentas.

La Tabla 1.2 proporciona varias estadísticas que resumen diferentes aspectos de la distribución. Los montos de las reclamaciones están en unidades de logaritmos de miles de dólares. La reclamación logarítmica promedio es 0.481, lo que corresponde a $1,617.77 (=1000 \(\exp(0.481)\)). Las reclamaciones más pequeñas y más grandes son -3.101 (45 dólares) y 3.912 (50,000 dólares), respectivamente.

Tabla 1.2: Summary Statistics of Massachusetts Automobile Bodily Injury Claims
Number Mean Median Standard Deviation Minimum Maximum 25th Percentile 75th Percentile
Claims 272 0.481 0.793 1.101 -3.101 3.912 -0.114 1.168

Para completar, aquí hay algunas definiciones. La muestra es el conjunto de datos disponibles para el análisis, denotado por \(y_1,\ldots,y_n\). Aquí, \(n\) es el número de observaciones, \(y_1\) representa la primera observación, \(y_2\) la segunda, y así sucesivamente hasta \(y_n\) para la \(n\)-ésima observación. Aquí hay algunas estadísticas de resumen importantes.

Estadísticas Básicas de Resumen

  • La media es el promedio de las observaciones, es decir, la suma de las observaciones dividida por el número de unidades. Usando notación algebraica, la media es \[ \overline{y}=\frac{1}{n}\left( y_1 + \cdots + y_n \right) = \frac{1}{n} \sum_{i=1}^{n} y_i. \]
  • La mediana es la observación central cuando las observaciones están ordenadas por tamaño. Es decir, es la observación en la que el 50% está por debajo de ella (y el 50% está por encima de ella).
  • La desviación estándar es una medida de la dispersión, o escala, de la distribución. Se calcula como \[ s_y = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}\left( y_i-\overline{y}\right) ^{2}} . \]
  • Un percentil es un número en el que una fracción específica de las observaciones está por debajo de él, cuando las observaciones están ordenadas por tamaño. Por ejemplo, el percentil 25 es aquel número en el que el 25% de las observaciones están por debajo de él.

Para ayudar a visualizar la distribución, la Figura 1.2 muestra un histograma de los datos. Aquí, la altura de cada rectángulo muestra la frecuencia relativa de observaciones que caen dentro del rango dado por su base. El histograma proporciona una impresión visual rápida de la distribución; muestra que el rango de los datos es aproximadamente (-4,4), la tendencia central es ligeramente mayor que cero y que la distribución es aproximadamente simétrica.

Aproximación de la Curva Normal. La Figura 1.2 también muestra una curva normal superpuesta, utilizando \(\overline{y}\) para \(\mu\) y \(s_y^{2}\) para \(\sigma ^{2}\). Con la curva normal, solo se requieren dos cantidades (\(\mu\) y \(\sigma ^{2}\)) para resumir toda la distribución. Por ejemplo, la Tabla 1.2 muestra que 1.168 es el percentil 75, que es aproximadamente la observación número 204 (\(=0.75\times 272\)) más grande de toda la muestra. De la ecuación (1.1) de la distribución normal, tenemos que \(z=(y-\mu )/\sigma\) es una normal estándar, de la cual 0.675 es el percentil 75. Así, \(\overline{y}+0.675s_y=\) \(0.481+0.675\times 1.101=1.224\) es el percentil 75 usando la aproximación de la curva normal.

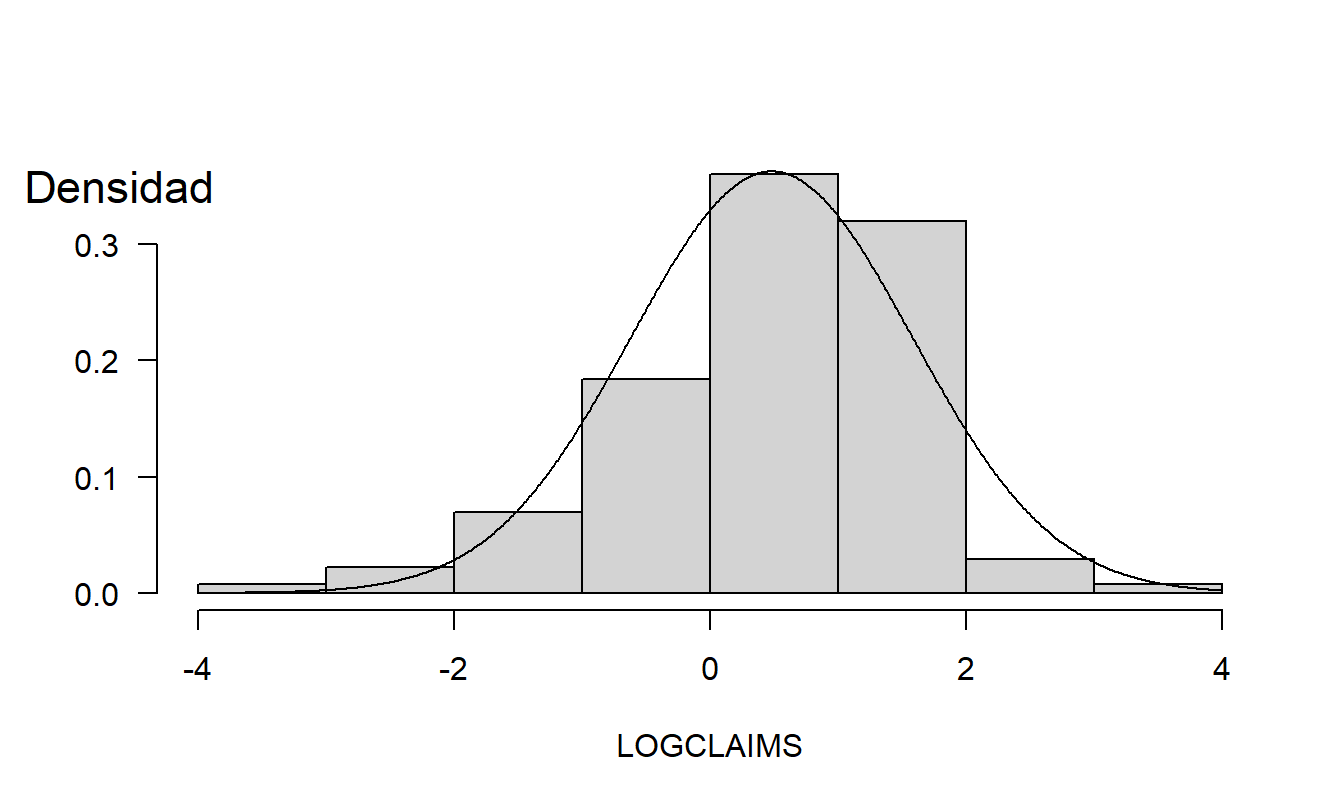
Frecuencia Relativa de Lesiones Corporales con Curva Normal Superpuesta.

Figura 1.2: Frecuencia Relativa de Lesiones Corporales con Curva Normal Superpuesta.

Código R para Producir la Figura 1.2

Diagrama de Caja. Una inspección visual rápida de la distribución de una variable puede revelar algunas características sorprendentes que están ocultas por estadísticas, medidas de resumen numéricas. El diagrama de caja, también conocido como diagrama de ‘caja y bigotes’, es uno de estos dispositivos gráficos. La Figura 1.3 ilustra un diagrama de caja para las reclamaciones por lesiones corporales. Aquí, la caja captura el 50% central de los datos, con las tres líneas horizontales que corresponden a los percentiles 75, 50 y 25, leyendo de arriba a abajo. Las líneas horizontales por encima y por debajo de la caja son los ‘bigotes’. El bigote superior es 1.5 veces el rango intercuartílico (la diferencia entre los percentiles 75 y 25) por encima del percentil 75. De manera similar, el bigote inferior es 1.5 veces el rango intercuartílico por debajo del percentil 25. Las observaciones individuales fuera de los bigotes se denotan con pequeños símbolos de trazado circulares, y se denominan ‘valores atípicos’.

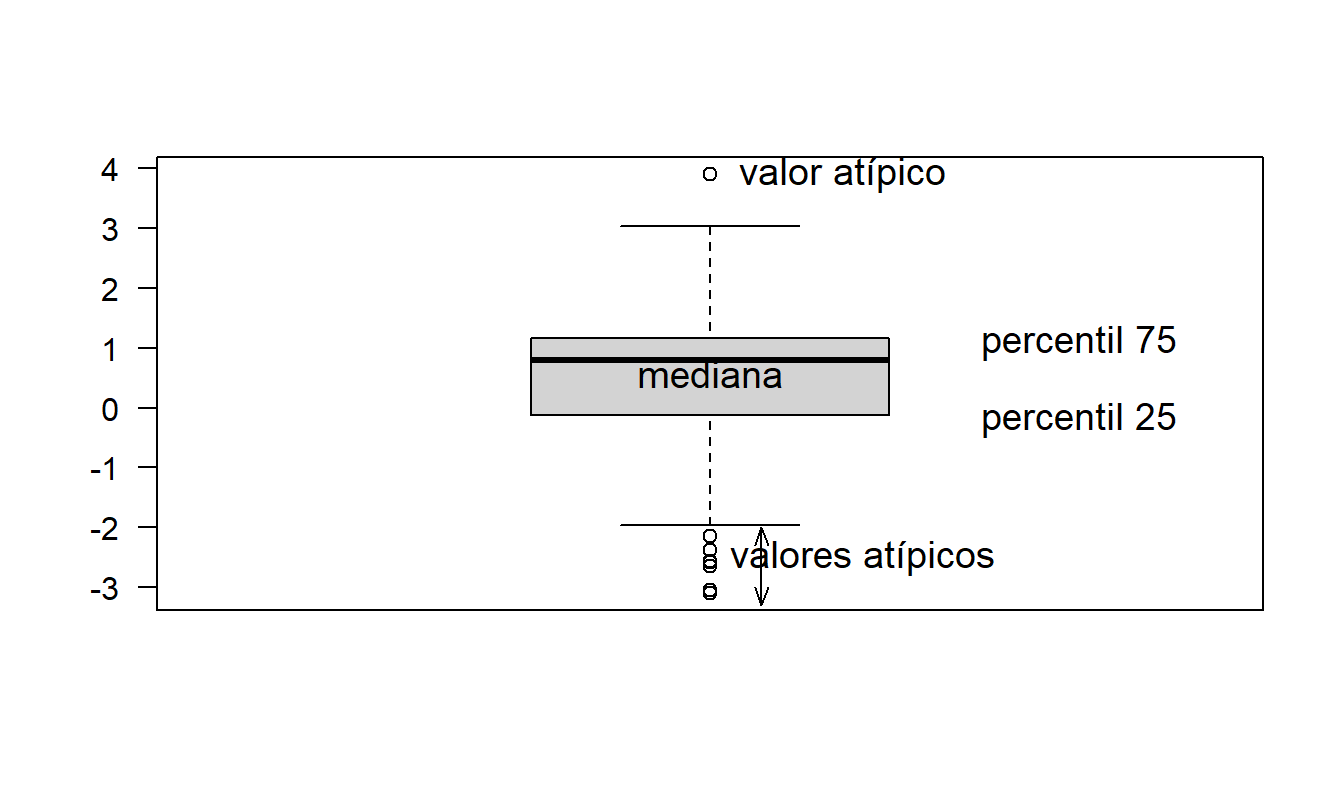
Diagrama de Caja de Reclamaciones por Lesiones Corporales.

Figura 1.3: Diagrama de Caja de Reclamaciones por Lesiones Corporales.

Código R para Producir la Figura 1.3

Los gráficos son herramientas poderosas; permiten a los analistas visualizar fácilmente relaciones no lineales que son difíciles de comprender cuando se expresan verbalmente o mediante fórmulas matemáticas. Sin embargo, debido a su gran flexibilidad, los gráficos también pueden engañar fácilmente al analista. El Capítulo 21 subrayará este punto. Por ejemplo, la Figura 1.4 es un re-dibujo de la Figura 1.2; la diferencia es que la Figura 1.4 usa más y más finos rectángulos. Este análisis más detallado revela la naturaleza asimétrica de la distribución de la muestra que no era evidente en la Figura 1.2.

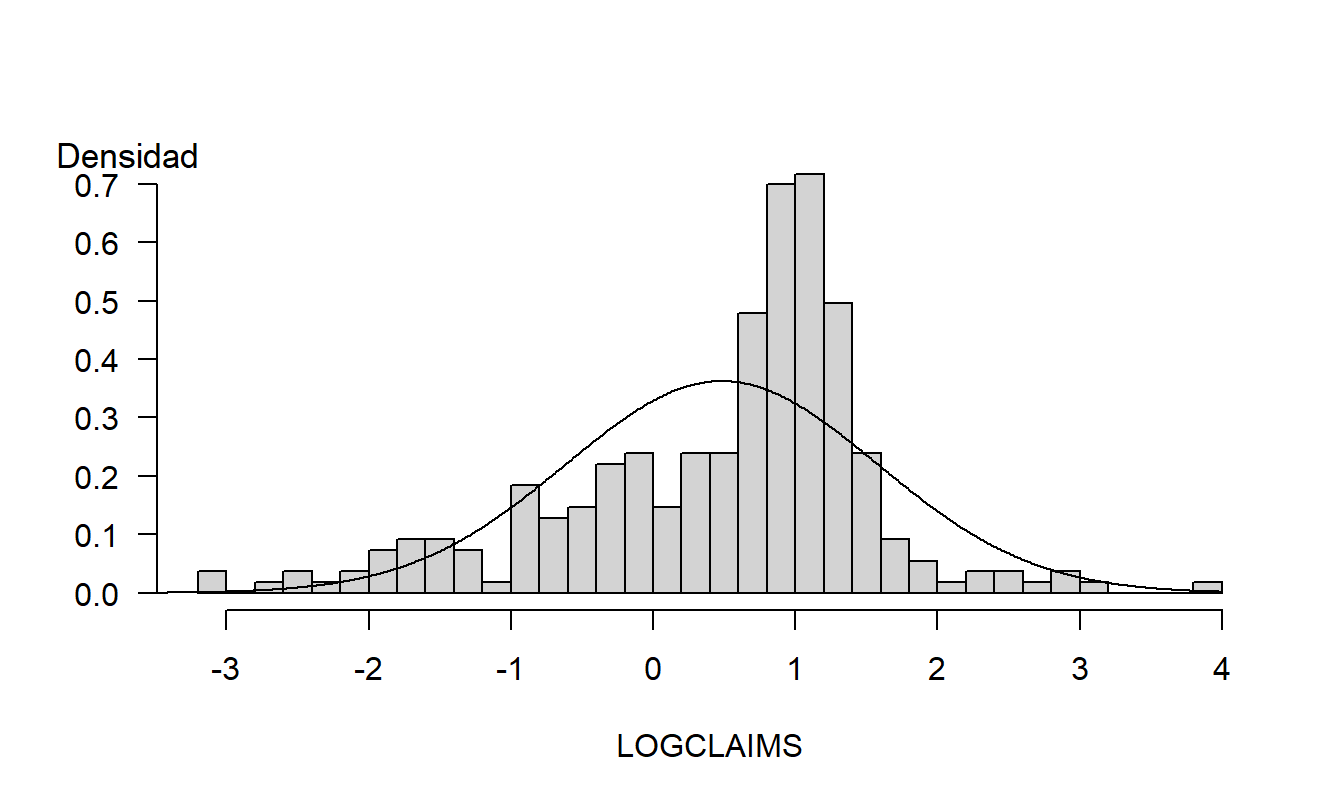
Re-dibujo de la Figura 1.2 con un número aumentado de rectángulos.

Figura 1.4: Re-dibujo de la Figura 1.2 con un número aumentado de rectángulos.

Código R para Producir la Figura 1.4

Gráficos Cuantiles-Cuantiles. Aumentar el número de rectángulos puede descubrir características que no eran evidentes antes; sin embargo, en general hay menos observaciones por rectángulo, lo que significa que la incertidumbre de la estimación de la frecuencia relativa aumenta. Esto representa un compromiso. En lugar de forzar al analista a tomar una decisión arbitraria sobre el número de rectángulos, una alternativa es usar un dispositivo gráfico para comparar una distribución con otra conocida, llamado gráfico de cuantiles-cuantiles, o qq.

La Figura 1.5 ilustra un gráfico \(qq\) para los datos de lesiones corporales utilizando la curva normal como distribución de referencia. Para cada punto, el eje vertical da el cuantil usando la distribución de la muestra. El eje horizontal da la cantidad correspondiente usando la curva normal. Por ejemplo, anteriormente consideramos el punto del percentil 75. Este punto aparece como (1.168, 0.675) en el gráfico. Para interpretar un gráfico \(qq\), si los puntos de los cuantiles se alinean a lo largo de la línea superpuesta, entonces la muestra y la distribución de referencia normal tienen la misma forma. (Esta línea se define conectando los percentiles 75 y 25).

En la Figura 1.5, los percentiles pequeños de la muestra son consistentemente más pequeños que los valores correspondientes de la normal estándar, lo que indica que la distribución está sesgada a la izquierda. La diferencia en los valores en los extremos de la distribución se debe a los valores atípicos mencionados anteriormente que también podrían interpretarse como que la distribución de la muestra tiene colas más grandes que la distribución de referencia normal.

Un gráfico \(qq\) de Reclamaciones por Lesiones Corporales, usando una distribución de referencia normal.

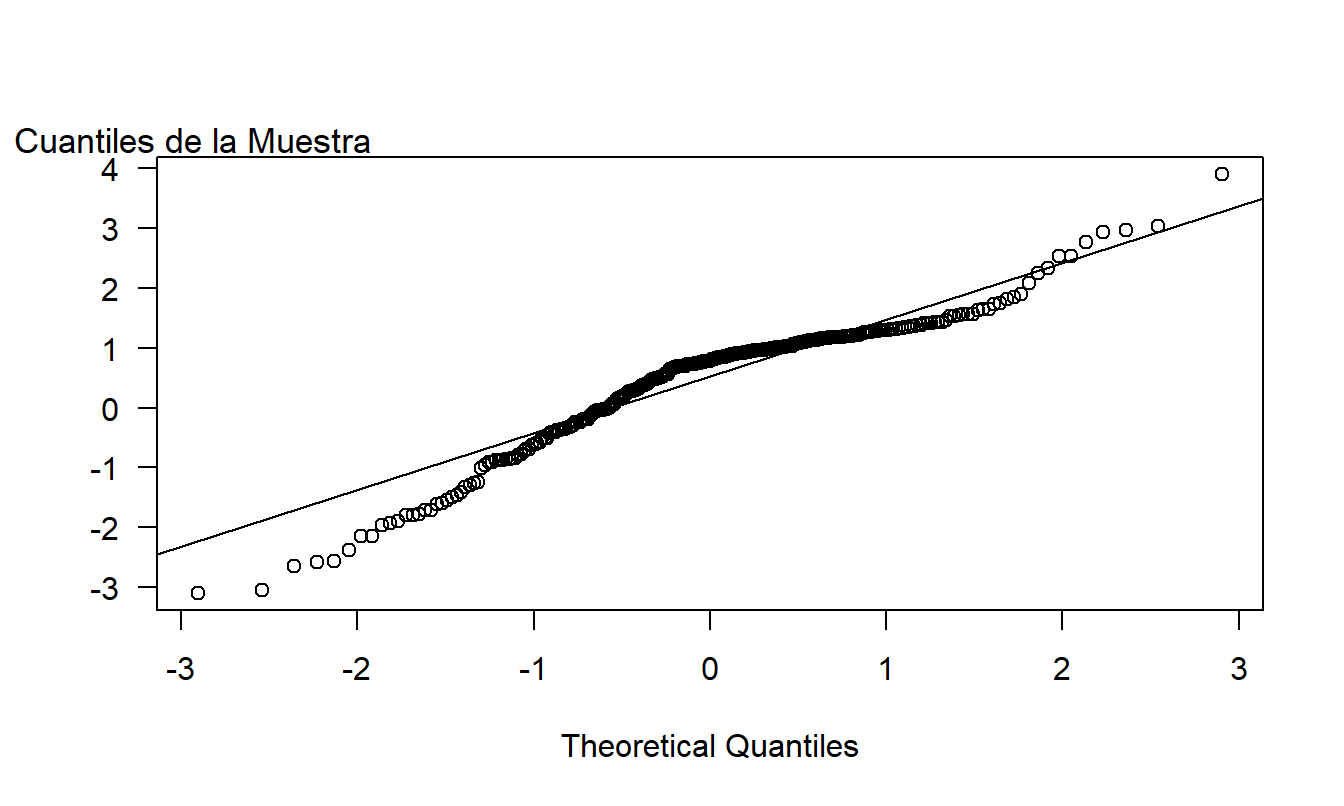
Figura 1.5: Un gráfico \(qq\) de Reclamaciones por Lesiones Corporales, usando una distribución de referencia normal.

Código R para Producir la Figura 1.5

1.3 Transformaciones de Potencia

En el ejemplo de la Sección 1.2, consideramos las reclamaciones sin justificar el uso de la escala logarítmica. Al analizar variables como los activos de las empresas, los salarios de los individuos y los precios de las viviendas en aplicaciones empresariales y económicas, es común considerar logaritmos en lugar de las unidades originales. Una transformación logarítmica mantiene el orden original (por ejemplo, los salarios altos siguen siendo altos en la escala de logaritmos de los salarios) pero sirve para ‘acercar’ los valores extremos de la distribución.

Para ilustrar, la Figura 1.6 muestra la distribución de las reclamaciones por lesiones corporales en (miles de) dólares. Para graficar los datos de manera significativa, se eliminó la observación más grande ($50,000) antes de hacer este gráfico. Incluso con esta observación eliminada, la Figura 1.6 muestra que la distribución está muy inclinada hacia la derecha, con varios valores grandes de reclamaciones apareciendo.

Las distribuciones que están inclinadas en una dirección u otra se conocen como sesgadas. La Figura 1.6 es un ejemplo de una distribución sesgada a la derecha, o sesgada positivamente. Aquí, la cola de la distribución a la derecha es más larga y hay una mayor concentración de masa a la izquierda. En contraste, una distribución sesgada a la izquierda, o sesgada negativamente, tiene una cola más larga a la izquierda y una mayor concentración de masa a la derecha. Muchas distribuciones de reclamaciones de seguros están sesgadas a la derecha (ver el texto de Klugman, Panjer y Willmot, 2008, para discusiones extensas). Como vimos en las Figuras 1.4 y 1.5, una transformación logarítmica produce una distribución que está solo ligeramente sesgada a la izquierda.

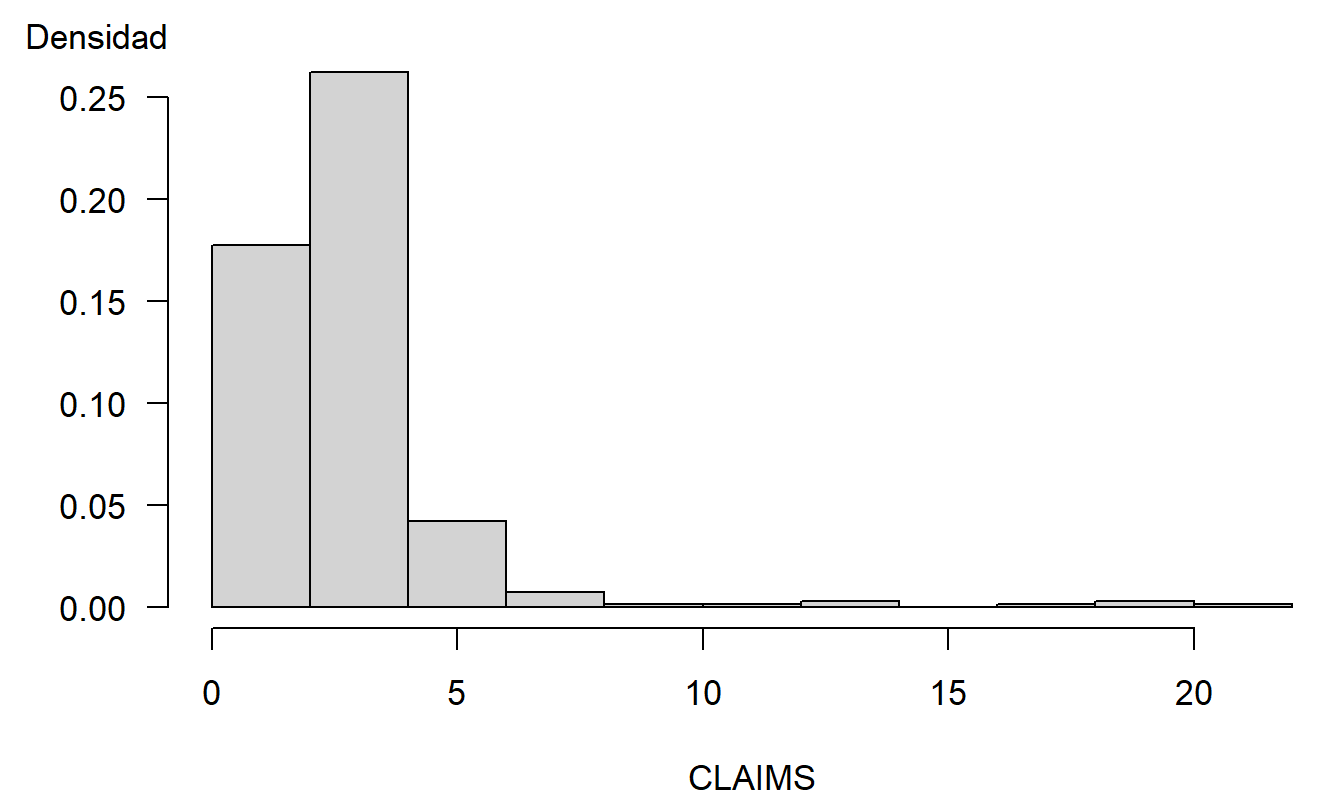
Distribución de Reclamaciones por Lesiones Corporales. Las observaciones están en (miles de) dólares con la observación más grande omitida.

Figura 1.6: Distribución de Reclamaciones por Lesiones Corporales. Las observaciones están en (miles de) dólares con la observación más grande omitida.

Código R para Producir la Figura 1.6

Las transformaciones logarítmicas se usan extensamente en el trabajo de estadística aplicada. Una ventaja es que sirven para simetrizar distribuciones que están sesgadas. Más generalmente, consideramos transformaciones de potencia, también conocidas como la familia de transformaciones de Box-Cox. Dentro de esta familia de transformaciones, en lugar de usar la respuesta \(y\), usamos una versión transformada o reescalada, \(y^{\lambda}\). Aquí, la potencia \(\lambda\) (lambda, una ‘l’ griega) es un número que puede ser especificado por el usuario. Los valores típicos de \(\lambda\) que se usan en la práctica son \(\lambda\)=1, 1/2, 0 o -1. Cuando usamos \(\lambda =0\), queremos decir \(\ln (y)\), es decir, la transformación logarítmica natural. Más formalmente, la familia de Box-Cox puede expresarse como \[ y^{(\lambda )}=\left\{ \begin{array}{ll} \frac{y^{\lambda }-1}{\lambda } & \lambda \neq 0 \\ \ln (y) & \lambda =0 \end{array} \right. . \]

Como veremos, porque las estimaciones de regresión no se ven afectadas por desplazamientos de ubicación y escala, en la práctica no necesitamos restar uno ni dividir por \(\lambda\) al reescalar la respuesta. La ventaja de la expresión anterior es que, si dejamos que \(\lambda\) se acerque a 0, entonces \(y^{(\lambda )}\) se acerca a \(\ln (y)\), a partir de algunos argumentos de cálculo sencillos.

Para ilustrar la utilidad de las transformaciones, simulamos 500 observaciones de una distribución chi-cuadrado con dos grados de libertad. El Apéndice A3.2 introduce esta distribución (que encontraremos nuevamente más adelante al estudiar el comportamiento de los estadísticos de prueba). El panel superior izquierdo de la Figura 1.7 muestra que la distribución original está muy sesgada hacia la derecha. Los otros paneles en la Figura 1.7 muestran los datos reescalados utilizando las transformaciones de raíz cuadrada, logarítmica y recíproca negativa. La transformación logarítmica, en el panel inferior izquierdo, proporciona la mejor aproximación a la simetría para este ejemplo. La transformación recíproca negativa se basa en \(\lambda =-1\), y luego multiplicando las observaciones reescaladas por menos uno, de modo que las observaciones grandes sigan siendo grandes.

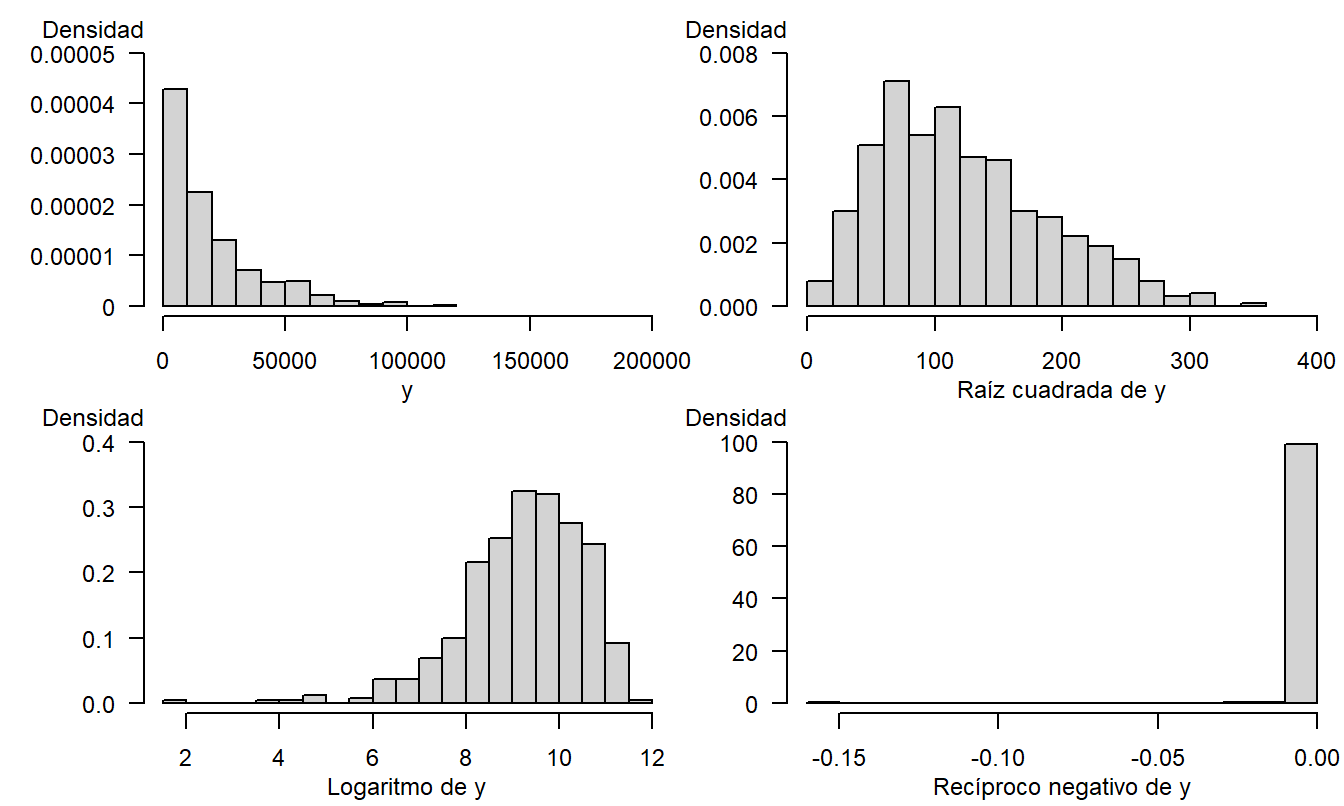
500 observaciones simuladas de una distribución chi-cuadrado. El panel superior izquierdo se basa en la distribución original. El superior derecho corresponde a la transformación de raíz cuadrada, el inferior izquierdo a la transformación logarítmica y el inferior derecho a la transformación recíproca negativa.

Figura 1.7: 500 observaciones simuladas de una distribución chi-cuadrado. El panel superior izquierdo se basa en la distribución original. El superior derecho corresponde a la transformación de raíz cuadrada, el inferior izquierdo a la transformación logarítmica y el inferior derecho a la transformación recíproca negativa.

Código R para Producir la Figura 1.7

1.4 Muestreo y el Papel de la Normalidad

Una estadística es una medida resumen de los datos, como una media, mediana o percentil. Las colecciones de estadísticas son muy útiles para analistas, tomadores de decisiones y consumidores cotidianos para comprender grandes cantidades de datos que representan situaciones complejas. Hasta este punto, nuestro enfoque ha sido introducir técnicas sensatas para resumir variables; técnicas que se usarán repetidamente a lo largo de este texto. Sin embargo, la verdadera utilidad de la disciplina de la estadística es su capacidad para decir algo sobre lo desconocido, no solo para resumir la información ya disponible. Con este fin, necesitamos hacer algunas suposiciones bastante formales sobre la manera en que se observan los datos. Como ciencia, una característica destacada de la estadística (como disciplina) es la capacidad de criticar estas suposiciones y ofrecer alternativas mejoradas en situaciones específicas.

Es costumbre suponer que los datos se extraen de una población más grande que estamos interesados en describir. El proceso de extracción de los datos se conoce como muestreo, o proceso generador de datos. Denotamos esta muestra como \(\{y_1,\ldots,y_n\}\). Para que podamos criticar y modificar estas suposiciones de muestreo, las enumeramos a continuación en detalle:

\[ \begin{array}{l} \hline \textbf{Suposiciones Básicas de Muestreo} \\ \hline 1. ~\mathrm{E~}y_i=\mu \\ 2. ~\mathrm{Var~}y_i=\sigma ^{2} \\ 3. ~\{y_i\} \text{ son independientes} \\ 4. ~\{y_i\} \text{ están distribuidos normalmente}. \\ \hline \end{array} \]

En esta configuración básica, \(\mu\) y \(\sigma ^{2}\) sirven como parámetros que describen la ubicación y escala de la población de origen. El objetivo es inferir algo sensato sobre ellos basándose en estadísticas como \(\overline{y}\) y \(s_y^{2}\). Para la tercera suposición, asumimos independencia entre las extracciones. En un esquema de muestreo, esto puede ser garantizado tomando una muestra aleatoria simple de una población. La cuarta suposición no es necesaria para muchos procedimientos de inferencia estadística porque los teoremas del límite central proporcionan una normalidad aproximada para muchas estadísticas de interés. Sin embargo, una justificación formal de algunas estadísticas, como las t-estadísticas, requiere esta suposición adicional.

La Sección 1.9 proporciona una declaración explícita de una versión del teorema del límite central, dando condiciones bajo las cuales \(\overline{y}\) está aproximadamente distribuido normalmente. Esta sección también discute un resultado relacionado, conocido como aproximación de Edgeworth, que muestra que la calidad de la aproximación normal es mejor para poblaciones de origen simétricas en comparación con distribuciones sesgadas.

¿Cómo se aplica esta discusión al estudio del análisis de regresión? Después de todo, hasta ahora nos hemos centrado solo en el promedio aritmético simple, \(\overline{y}\). En capítulos posteriores, enfatizaremos que la regresión lineal es el estudio de promedios ponderados; específicamente, muchos coeficientes de regresión pueden expresarse como promedios ponderados con pesos apropiadamente elegidos. Los teoremas de límite central y aproximación de Edgeworth están disponibles para promedios ponderados; estos resultados asegurarán la normalidad aproximada de los coeficientes de regresión. Para usar aproximaciones de la curva normal en un contexto de regresión, a menudo transformaremos variables para lograr una simetría aproximada.

1.5 Regresión y Diseños de Muestreo

La aproximación a la normalidad será un tema importante en las aplicaciones prácticas de la regresión lineal. Las Partes I y II de este libro se centran en la regresión lineal, donde aprenderemos conceptos básicos de regresión y diseño de muestreo. La Parte III se centrará en la regresión no lineal, que involucra respuestas binarias, de conteo y de colas pesadas, donde la normalidad no es la distribución de referencia más útil. Las ideas sobre conceptos básicos y diseño también se usarán en el contexto no lineal.

En el análisis de regresión, nos enfocamos en una medición de interés y la llamamos variable dependiente. Otras mediciones se usan como variables explicativas. Un objetivo es comparar las diferencias en la variable dependiente en términos de diferencias en las variables explicativas. Como se mencionó en la Sección 1.1, la regresión se usa extensamente en muchos campos científicos. Tabla 1.3 enumera términos alternativos que puedes encontrar al leer aplicaciones de regresión.

Tabla 1.3. Terminología para Variables de Regresión

\[ {\small \begin{array}{ll}\hline\hline y-\text{Variable} & x-\text{Variable} \\\hline \text{Resultado de interés} & \text{Variable explicativa} \\ \text{Variable dependiente} & \text{Variable independiente} \\ \text{Variable endógena} & \text{Variable exógena} \\ \text{Respuesta} & \text{Tratamiento} \\ \text{Regresando} & \text{Regresor} \\ \text{Variable del lado izquierdo} & \text{Variable del lado derecho} \\ \text{Variable explicada} & \text{Variable predictora} \\ \text{Resultado} & \text{Entrada} \\ \hline \end{array} } \]

En la última parte del siglo XIX y principios del siglo XX, la estadística comenzó a tener un impacto importante en el desarrollo de la ciencia experimental. Las ciencias experimentales a menudo utilizan estudios diseñados, donde los datos están bajo el control de un analista. Los estudios diseñados se realizan en entornos de laboratorio, donde hay restricciones físicas estrictas en cada variable que un investigador considera importante. Los estudios diseñados también ocurren en experimentos de campo más grandes, donde los mecanismos de control son diferentes a los de los entornos de laboratorio. La agricultura y la medicina utilizan estudios diseñados. Los datos de un estudio diseñado se dicen que son datos experimentales.

Para ilustrar, un ejemplo clásico es considerar el rendimiento de un cultivo como el maíz, donde cada uno de varios parcelas de tierra (las observaciones) se asigna a varios niveles de fertilizante. El objetivo es determinar el efecto del fertilizante (la variable explicativa) en el rendimiento del maíz (la variable de respuesta). Aunque los investigadores intentan hacer que las parcelas de tierra sean lo más similares posible, inevitablemente surgen diferencias. Los investigadores agrícolas utilizan técnicas de aleatorización para asignar diferentes niveles de fertilizante a cada parcela de tierra. De esta manera, los analistas pueden explicar la variación en los rendimientos de maíz en términos de la variación de los niveles de fertilizante. A través del uso de técnicas de aleatorización, los investigadores que utilizan estudios diseñados pueden inferir que el tratamiento tiene un efecto causal sobre la respuesta. El Capítulo 6 discute la causalidad más a fondo.

Ejemplo: Experimento de Seguro de Salud Rand. ¿Cómo están relacionados los gastos en atención médica con la demanda de seguro? Muchos estudios han establecido una relación positiva entre la cantidad gastada en atención médica y la demanda de seguro de salud. Aquellos en mala salud anticipan usar más servicios médicos que las personas en buena o regular salud y buscarán niveles más altos de seguro de salud para compensar estos gastos anticipados. Obtienen este seguro adicional al (i) seleccionar un plan de seguro de salud más generoso de un empleador, (ii) elegir un empleador con un plan de seguro de salud más generoso o (iii) pagar más por un seguro de salud individual. Así, es difícil desenredar la relación causa-efecto de los gastos en atención médica y la disponibilidad de seguro de salud.

Un estudio reportado por Manning et al. (1987) buscó responder a esta pregunta utilizando un experimento cuidadosamente diseñado. En este estudio, los hogares inscritos de seis ciudades, entre noviembre de 1974 y febrero de 1977, fueron asignados aleatoriamente a uno de 14 planes de seguro diferentes. Estos planes variaban según los elementos de participación en los costos, la tasa de coaseguro (el porcentaje pagado de los gastos de bolsillo que variaba entre 0, 25, 50 y 95%) así como el deducible (5, 10 o 15 por ciento del ingreso familiar, hasta un máximo de $1,000). Así, hubo una asignación aleatoria a los niveles del tratamiento, la cantidad de seguro de salud. El estudio encontró que los planes más favorables resultaron en mayores gastos totales, incluso después de controlar el estado de salud de los participantes.

Para la ciencia actuarial y otras ciencias sociales, los estudios diseñados son la excepción más que la regla. Por ejemplo, si queremos estudiar los efectos del tabaquismo en la mortalidad, es muy poco probable que podamos conseguir que los participantes en el estudio acepten ser asignados aleatoriamente a grupos de fumadores/no fumadores durante varios años solo para observar sus patrones de mortalidad. Al igual que en el estudio de Galton de la Sección 1.1, los investigadores en ciencias sociales generalmente trabajan con datos observacionales. Los datos observacionales no están bajo el control del analista.

Con datos observacionales, no podemos inferir relaciones causales, pero podemos introducir medidas de asociación. Para ilustrar, en los datos de Galton, es evidente que los padres ‘altos’ tienden a tener hijos ‘altos’ y, a la inversa, los padres ‘bajos’ tienden a tener hijos ‘bajos’. El Capítulo 2 introducirá la correlación y otras medidas de asociación. Sin embargo, no podemos inferir causalidad a partir de los datos. Por ejemplo, puede haber otra variable, como la dieta familiar, que esté relacionada con ambas variables. Una buena dieta en la familia podría estar asociada con alturas altas de los padres y de los hijos adultos, mientras que una dieta pobre limita el crecimiento. Si ese fuera el caso, llamaríamos a la dieta familiar una variable confusora.

En experimentos diseñados como el Experimento de Seguro de Salud Rand, podemos controlar los efectos de variables como el estado de salud mediante métodos de asignación aleatoria. En estudios observacionales, usamos control estadístico, en lugar de control experimental. Para ilustrar, en los datos de Galton, podríamos dividir nuestras observaciones en dos grupos, uno para ‘buena dieta familiar’ y otro para ‘mala dieta familiar’, y examinar la relación entre la altura de los padres y la de los hijos para cada subgrupo. Esta es la esencia del método de regresión, comparar un \(y\) y un \(x\), ‘controlando’ los efectos de otras variables explicativas.

Por supuesto, para usar control estadístico y métodos de regresión, uno debe registrar la dieta familiar y cualquier otra medida de altura que pueda confundir los efectos de la altura de los padres en la altura de su hijo adulto. La dificultad en diseñar estudios es tratar de imaginar todas las variables que podrían afectar una variable de respuesta, una tarea imposible en la mayoría de los problemas de interés en ciencias sociales. Para dar algunas orientaciones sobre cuándo ‘es suficiente’, el Capítulo 6 discutirá medidas de la importancia de una variable explicativa y su impacto en la selección del modelo.

1.6 Aplicaciones Actuariales de la Regresión

Este libro introduce un método estadístico, el análisis de regresión. La introducción está organizada en torno a la tríada tradicional de la inferencia estadística:

  • prueba de hipótesis,
  • estimación y
  • predicción.

Además, este libro muestra cómo esta metodología puede ser utilizada en aplicaciones que probablemente serán de interés para los actuarios y otros analistas de riesgos. Como tal, es útil comenzar con las tres áreas tradicionales de aplicaciones actuariales:

  • tarificación,
  • reservas y
  • pruebas de solvencia.

Tarificación y selección adversa. El análisis de regresión puede utilizarse para determinar los precios de seguros para muchas líneas de negocio. Por ejemplo, en el seguro de automóviles de pasajeros privados, las reclamaciones esperadas varían según el género del asegurado, la edad, la ubicación (ciudad versus rural), el propósito del vehículo (trabajo o placer) y una serie de otras variables explicativas. La regresión puede utilizarse para identificar las variables que son determinantes importantes de las reclamaciones esperadas.

En mercados competitivos, las compañías de seguros no usan el mismo precio para todos los asegurados. Si lo hicieran, los ‘buenos riesgos’, aquellos con reclamaciones esperadas inferiores a la media, pagarían de más y abandonarían la compañía. En contraste, los ‘malos riesgos’, aquellos con reclamaciones esperadas superiores a la media, permanecerían con la compañía. Si la compañía continuara con esta política de precios plana, las primas aumentarían (para compensar las reclamaciones de la creciente proporción de malos riesgos) y la participación en el mercado disminuiría a medida que la compañía pierde buenos riesgos. Este problema se conoce como ‘selección adversa’. Usando un conjunto apropiado de variables explicativas, se pueden desarrollar sistemas de clasificación para que cada asegurado pague su parte justa.

Reservas y pruebas de solvencia. Tanto la constitución de reservas como las pruebas de solvencia se preocupan por predecir si las obligaciones asociadas con un grupo de pólizas excederán el capital destinado a cumplir con las obligaciones derivadas de las pólizas. La constitución de reservas implica determinar la cantidad apropiada de capital para cumplir con estas obligaciones. Las pruebas de solvencia se centran en evaluar la adecuación del capital para financiar las obligaciones de un bloque de negocio. En algunas áreas de práctica, la regresión puede usarse para pronosticar futuras obligaciones y ayudar a determinar las reservas (ver, por ejemplo, el Capítulo 19). La regresión también puede utilizarse para comparar las características de empresas saludables y financieramente angustiadas para pruebas de solvencia (ver, por ejemplo, el Capítulo 14).

Otras aplicaciones en gestión de riesgos. El análisis de regresión es una herramienta cuantitativa que puede aplicarse en una amplia variedad de problemas de negocio, no solo en las áreas tradicionales de tarificación, reservas y pruebas de solvencia. Al familiarizarse con el análisis de regresión, los actuarios tendrán otra habilidad cuantitativa que puede aplicarse a problemas generales relacionados con la seguridad financiera de personas, empresas y organizaciones gubernamentales. Para ayudarte a desarrollar ideas, este libro proporciona muchos ejemplos de aplicaciones potenciales ‘no actuariales’ a través de viñetas destacadas etiquetadas como ‘ejemplos’ y conjuntos de datos ilustrativos.

Para entender las posibles aplicaciones de la regresión, comienza revisando los varios conjuntos de datos presentados en los Ejercicios del Capítulo 1. Incluso si no completas los ejercicios para fortalecer tus habilidades de resumen de datos (que requieren el uso de una computadora), una revisión de las descripciones de los problemas te ayudará a familiarizarte con los tipos de aplicaciones en las que un actuario podría usar técnicas de regresión.

1.7 Lecturas Adicionales y Referencias

Este libro introduce herramientas de regresión y series temporales que son más relevantes para los actuarios y otros analistas de riesgos financieros. Afortunadamente, existen otras fuentes que proporcionan excelentes introducciones a estos temas estadísticos (aunque no desde un punto de vista de gestión de riesgos). En particular, para los analistas que desean especializarse en estadística, es útil obtener otra perspectiva. Para regresión, recomiendo Weisburg (2005) y Faraway (2005). Para series temporales, Diebold (2004) es una buena fuente. Además, Klugman, Panjer y Willmot (2008) proporciona una buena introducción a las aplicaciones actuariales de la estadística; este libro está destinado a complementar el libro de Klugman et al. al centrarse en métodos de regresión y series temporales.

Referencias del Capítulo

  • Beard, Robert E., Teivo Pentik"{a}inen and Erkki Pesonen (1984). Risk Theory: The Stochastic Basis of Insurance (Third Edition). Chapman & Hall, New York.
  • Diebold, Francis. X. (2004). Elements of Forecasting, Third Edition. Thomson, South-Western, Mason, Ohio.
  • Faraway, Julian J. (2005). Linear Models in R. Chapman & Hall/CRC, New York.
  • Hogg, Robert V. (1972). On statistical education. The American Statistician 26, 8-11.
  • Klugman, Stuart A, Harry H. Panjer and Gordon E. Willmot (2008). Loss Models: From Data to Decisions. John Wiley & Sons, Hoboken, New Jersey.
  • Manning, Willard G., Joseph P. Newhouse, Naihua Duan, Emmett B. Keeler, Arleen Leibowitz and M. Susan Marquis (1987). Health insurance and the demand for medical care: Evidence from a randomized experiment. American Economic Review 77, No. 3, 251-277.
  • Rempala, Grzegorz A. and Richard A. Derrig (2005). Modeling hidden exposures in claim severity via the EM algorithm. North American Actuarial Journal 9, No. 2, 108-128.
  • Singer, Judith D. and Willett, J. B. (1990). Improving the teaching of applied statistics: Putting the data back into data analysis. The American Statistician 44, 223-230.
  • Stigler, Steven M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900. The Belknap Press of Harvard University Press, Cambridge, MA.
  • Weisberg, Sanford (2005). Applied Linear Regression, Third Edition. John Wiley & Sons, New York.

1.8 Ejercicios

1.1 Gastos de Salud de MEPS. Este ejercicio considera datos de la Encuesta de Gastos Médicos (MEPS), realizada por la Agencia de Investigación y Calidad en Salud de EE.UU. (AHRQ). MEPS es una encuesta probabilística que proporciona estimaciones nacionalmente representativas del uso de atención médica, gastos, fuentes de pago y cobertura de seguros para la población civil de EE.UU. Esta encuesta recopila información detallada sobre episodios de atención médica de cada tipo de servicio, incluyendo visitas a consultorios médicos, visitas a salas de emergencia hospitalarias, visitas a hospitales ambulatorios, estancias hospitalarias, otras visitas a proveedores médicos y uso de medicamentos prescritos. Esta información detallada permite desarrollar modelos de utilización de atención médica para predecir futuros gastos. Puedes obtener más información sobre MEPS en http://www.meps.ahrq.gov/mepsweb/.

Consideramos los datos de MEPS de los paneles 7 y 8 de 2003, que consisten en 18,735 individuos entre las edades de 18 y 65 años. De esta muestra, tomamos una muestra aleatoria de 2,000 individuos que aparecen en el archivo ‘HealthExpend’. De esta muestra, hay 157 individuos que tuvieron gastos hospitalarios positivos. También hay 1,352 que tuvieron gastos ambulatorios positivos. Analizaremos estas dos muestras por separado.

Nuestras variables dependientes consisten en las cantidades de gastos para visitas hospitalarias (EXPENDIP) y ambulatorias (EXPENDOP). Para MEPS, los eventos ambulatorios incluyen visitas al departamento ambulatorio del hospital, visitas a proveedores en consultorios y visitas a salas de emergencia, excluyendo servicios dentales. (Los servicios dentales, en comparación con otros tipos de servicios de atención médica, son más predecibles y ocurren de manera más regular). Las estancias hospitalarias con la misma fecha de admisión y alta, conocidas como ‘estancias de cero noches’, se incluyeron en los recuentos y gastos ambulatorios. (Los pagos asociados con visitas a salas de emergencia que precedieron inmediatamente a una estancia hospitalaria se incluyeron en los gastos hospitalarios. Los medicamentos prescritos que se pueden vincular a las admisiones hospitalarias se incluyeron en los gastos hospitalarios, no en la utilización ambulatoria).

Parte 1: Usa solo los 157 individuos que tuvieron gastos hospitalarios positivos y realiza el siguiente análisis.

  1. Calcula estadísticas descriptivas para los gastos hospitalarios (EXPENDIP).
    • a(i). ¿Cuál es el gasto típico (media y mediana)?
    • a(ii). ¿Cómo se compara la desviación estándar con la media? ¿Los datos parecen estar sesgados?
  2. Calcula un diagrama de caja, un histograma y un gráfico \(qq\) (normal) para EXPENDIP. Comenta sobre la forma de la distribución.
  3. Transformaciones.
    • c(i). Realiza una transformación de raíz cuadrada de los gastos hospitalarios. Resume la distribución resultante usando un histograma y un gráfico \(qq\). ¿Parece estar aproximadamente distribuida normalmente?
    • c(ii). Realiza una transformación logarítmica (natural) de los gastos hospitalarios. Resume la distribución resultante usando un histograma y un gráfico \(qq\). ¿Parece estar aproximadamente distribuida normalmente?

Parte 2: Usa solo los 1,352 individuos que tuvieron gastos ambulatorios positivos.

  1. Repite la parte (a) y calcula histogramas para los gastos y los gastos logarítmicos. Comenta sobre la normalidad aproximada de cada histograma.

1.2 Utilización de Hogares de Cuidado de Ancianos. Este ejercicio considera datos de hogares de cuidado de ancianos proporcionados por el Departamento de Salud y Servicios Familiares de Wisconsin (DHFS). El programa Medicaid del Estado de Wisconsin financia el cuidado en hogares de cuidado de ancianos para individuos que califican en base a necesidades y estado financiero. Como parte de las condiciones de participación, los hogares de cuidado de ancianos certificados por Medicaid deben presentar un informe de costos anual al DHFS, resumiendo el volumen y costo del cuidado proporcionado a todos sus residentes, financiados por Medicaid y de otro tipo. Estos informes de costos son auditados por el personal del DHFS y forman la base para las tasas diarias de pago de Medicaid específicas para cada instalación para los períodos subsiguientes. Los datos están disponibles públicamente; consulta [http://dhs.wisconsin.gov] para más información.

El DHFS está interesado en técnicas predictivas que proporcionen pronósticos de utilización confiables para actualizar su programa de tasas de financiamiento de Medicaid para instalaciones de cuidado de ancianos. En esta tarea, consideramos los datos en el archivo ‘WiscNursingHome’ en los años de informe de costos 2000 y 2001. Hay 362 instalaciones en 2000 y 355 instalaciones en 2001. Típicamente, la utilización del cuidado en hogares de cuidado de ancianos se mide en días de paciente (‘días de paciente’ es el número de días que cada paciente estuvo en la instalación, sumado sobre todos los pacientes). Para este ejercicio, definimos la variable de resultado como años totales de pacientes (TPY), el número total de días de pacientes en el período de informe de costos dividido por el número de días operativos de la instalación en el período de informe de costos (ver Rosenberg et al., 2007, Apéndice 1, para una discusión adicional sobre esta elección). El número de camas (NUMBED) y el metraje cuadrado (SQRFOOT) del hogar de cuidado de ancianos miden el tamaño de la instalación. No sorprende que estas variables sean importantes predictores de TPY.

Parte 1: Usa los datos del año de informe de costos 2000 y realiza el siguiente análisis.

  1. Calcula estadísticas descriptivas para TPY, NUMBED y SQRFOOT.
  2. Resume la distribución de TPY usando un histograma y un gráfico \(qq\). ¿Parece estar aproximadamente distribuida normalmente?
  3. Transformaciones. Realiza una transformación logarítmica (natural) de TPY (LOGTPY). Resume la distribución resultante usando un histograma y un gráfico \(qq\). ¿Parece estar aproximadamente distribuida normalmente?

Parte 2: Usa los datos del año de informe de costos 2001 y repite las partes (a) y (c).

1.3 Reclamaciones de Seguros de Automóviles. Como analista actuarial, estás trabajando con una gran compañía de seguros para ayudarles a entender la distribución de sus reclamaciones para sus pólizas de automóviles particulares. Tienes disponibles datos de reclamaciones para un año reciente, que consisten en:

  • STATE CODE: códigos del 01 al 17 utilizados, con cada código asignado aleatoriamente a un estado real.
  • CLASS: clase de calificación del operador, basada en edad, género, estado civil y uso del vehículo.
  • GENDER: género del operador.
  • AGE: edad del operador.
  • PAID: monto pagado para resolver y cerrar una reclamación.

Te estás enfocando en conductores mayores de 50 años, para los cuales hay \(n = 6,773\) reclamaciones disponibles.

Examina el histograma del monto PAID y comenta sobre la simetría. Crea una nueva variable, las reclamaciones pagadas en logaritmo natural, LNPAID. Crea un histograma y un gráfico \(qq\) de LNPAID. Comenta sobre la simetría de esta variable.

1.4 Costos Hospitalarios. Supongamos que eres un actuario de beneficios para empleados trabajando con una empresa de tamaño mediano en Wisconsin. Esta empresa está considerando ofrecer, por primera vez en su industria, cobertura de seguro hospitalario para los hijos dependientes de sus empleados. Tienes acceso a los registros de la empresa y, por lo tanto, tienes disponibles el número, edad y género de los hijos dependientes, pero no tienes otra información sobre los costos hospitalarios de la empresa. En particular, ninguna empresa en esta industria ha ofrecido esta cobertura, por lo que tienes poca experiencia histórica en la industria sobre la cual puedas prever los reclamos esperados.

Recopilas datos del Nationwide Inpatient Sample del Healthcare Cost and Utilization Project (NIS-HCUP), una encuesta nacional de costos hospitalarios realizada por la Agencia de Investigación y Calidad en Salud de EE.UU. (AHRQ). Restringes la consideración a hospitales de Wisconsin y analizas una muestra aleatoria de \(n=500\) reclamaciones de datos de 2003. Aunque los datos provienen de registros hospitalarios, están organizados por alta individual y por lo tanto tienes información sobre la edad y el género del paciente dado de alta. Específicamente, consideras pacientes de 0 a 17 años. En un proyecto separado, considerarás la frecuencia de hospitalización. Para este proyecto, el objetivo es modelar la gravedad de los cargos hospitalarios, por edad y género.

  1. Examina la distribución de la variable dependiente, TOTCHG. Haz esto creando un histograma y luego un gráfico \(qq\), comparando el empírico con una distribución normal.
  2. Realiza una transformación logarítmica natural y llama a la nueva variable LNTOTCHG. Examina la distribución de esta variable transformada. Para visualizar la relación logarítmica, traza LNTOTCHG frente a TOTCHG.

1.5 Reclamaciones de Seguros de Lesiones Automovilísticas. Consideramos datos de reclamaciones por lesiones en automóviles utilizando datos del Insurance Research Council (IRC), una división del American Institute for Chartered Property Casualty Underwriters y del Insurance Institute of America. Los datos, recopilados en 2002, contienen información sobre la demografía del reclamante, la participación del abogado y la pérdida económica (LOSS, en miles), entre otras variables. Aquí analizamos una muestra de \(n=1,340\) pérdidas de un solo estado. El estudio completo de 2002 contiene más de 70,000 reclamaciones cerradas basadas en datos de treinta y dos aseguradoras. El IRC realizó estudios similares en 1977, 1987, 1992 y 1997.

  1. Calcula las estadísticas descriptivas para la pérdida económica total (LOSS). ¿Cuál es la pérdida típica?

  2. Calcula un histograma y un gráfico \(qq\) (normal) para LOSS. Comenta sobre la forma de la distribución.

  3. Divide el conjunto de datos en dos submuestras, una correspondiente a las reclamaciones que involucraron a un ATTORNEY (=1) y otra en la que no se involucró un ATTORNEY (=2).

    • c(i). Para cada submuestra, calcula la pérdida típica. ¿Parece haber una diferencia en las pérdidas típicas según la participación del abogado?
    • c(ii) Para comparar las distribuciones, calcula un diagrama de caja (boxplot) por nivel de participación del abogado.
    • c(iii). Para cada submuestra, calcula un histograma y un gráfico \(qq\). Compara las dos distribuciones entre sí.

1.6 Gastos de la Compañía de Seguros. Al igual que otros negocios, las compañías de seguros buscan minimizar los gastos asociados con la realización de negocios para mejorar la rentabilidad. Para estudiar los gastos, este ejercicio examina una muestra aleatoria de 500 compañías de seguros de la base de datos de la National Association of Insurance Commissioners (NAIC) de más de 3,000 compañías. La NAIC mantiene una de las bases de datos regulatorias de seguros más grandes del mundo; consideramos aquí datos basados en los informes anuales de 2005 para todas las compañías de seguros de propiedad y casualty en los Estados Unidos. Los informes anuales son estados financieros que utilizan principios contables estatutarios.

Específicamente, nuestra variable dependiente es EXPENSES, los gastos no relacionados con reclamaciones para una compañía. Aunque no es necesario para este ejercicio, los gastos no relacionados con reclamaciones se basan en tres componentes: ajuste de pérdidas no asignadas, gastos de suscripción y gastos de inversión. El gasto por ajuste de pérdidas no asignadas es el gasto no directamente atribuible a una reclamación pero que está asociado indirectamente con la resolución de reclamaciones; incluye elementos como los salarios de los ajustadores de reclamaciones, honorarios legales, costos judiciales, testigos expertos y costos de investigación. Los gastos de suscripción consisten en costos de adquisición de pólizas, como comisiones, así como la parte de los gastos administrativos, generales y otros atribuibles a las operaciones de suscripción. Los gastos de inversión son aquellos gastos relacionados con las actividades de inversión del asegurador.

  1. Examina la distribución de la variable dependiente, EXPENSES. Haz esto creando un histograma y luego un gráfico \(qq\), comparando el empírico con una distribución normal.
  2. Realiza una transformación logarítmica natural y examina la distribución de esta variable transformada. ¿Ha ayudado la transformación a simetrizar la distribución?

1.7 Esperanzas de Vida Nacionales. ¿Quién está haciendo bien el cuidado de la salud? Las decisiones sobre la atención médica se toman a nivel individual, corporativo y gubernamental. Prácticamente todas las personas, corporaciones y gobiernos tienen su propia perspectiva sobre la atención médica; estas diferentes perspectivas dan lugar a una amplia variedad de sistemas para gestionar la atención médica. Comparar diferentes sistemas de atención médica nos ayuda a aprender sobre enfoques distintos al nuestro, lo que a su vez nos ayuda a tomar mejores decisiones al diseñar sistemas mejorados.

Aquí, consideramos los sistemas de atención médica de \(n=185\) países en todo el mundo. Como medida de la calidad de la atención, utilizamos LIFEEXP, la esperanza de vida al nacer. Esta variable dependiente, con varias variables explicativas, se enumeran en [Tabla 1.4]. A partir de esta tabla, notarás que aunque hay 185 países considerados en este estudio, no todos los países proporcionaron información para cada variable. Los datos no disponibles se indican en la columna Num Miss. Los datos provienen del Informe sobre el Desarrollo Humano de las Naciones Unidas (UN).

  1. Examina la distribución de la variable dependiente, LIFEEXP. Haz esto creando un histograma y luego un gráfico \(qq\), comparando el empírico con una distribución normal.
  2. Realiza una transformación logarítmica natural y examina la distribución de esta variable transformada. ¿Ha ayudado la transformación a simetrizar la distribución?

\[ \small{ \begin{array}{ll|crrrrr} \hline & & Num & & & Std & Mini- & Maxi- \\ Variable & Description & Miss & Mean & Median & Dev & mum & mum \\\hline BIRTH & \text{ Births attended by skilled} & 7 & 78.25 & 92.00 & 26.42 & 6.00 & 100.00 \\ ~~ATTEND& ~~ \text{ health personnel} (\%)\\ FEMALE & \text{ Legislators, senior officials} & 87 & 29.07 & 30.00 & 11.71 & 2.00 & 58.00 \\ ~~BOSS& ~~ \text{ and managers, % female }\\ FERTILITY & \text{ Total fertility rate,}& 4 & 3.19 & 2.70 & 1.71 & 0.90 & 7.50 \\ & ~~ \text{ births per woman }& \\ GDP & \text{ Gross domestic product,} & 7 & 247.55 & 14.20 & 1,055.69 & 0.10 & 12,416.50 \\ & ~~\text{ in billions of USD} \\ HEALTH& \text{ 2004 Health expenditure} & 5 & 718.01 & 297.50 & 1,037.01 & 15.00 & 6,096.00 \\ ~~ EXPEND & ~~ \text{ per capita, PPP in USD} \\ ILLITERATE & \text{ Adult illiteracy rate,} & 14 & 17.69 & 10.10 & 19.86 & 0.20 & 76.40 \\ & ~~ \% \text{ aged 15 and older} & \\ PHYSICIAN & \text{ Physicians,}& 3 & 146.08 & 107.50 & 138.55 & 2.00 & 591.00 \\ & ~~ \text{ per 100,000 people} \\ POP & \text{ 2005 population,} & 1 & 35.36 & 7.80 & 131.70 & 0.10 & 1,313.00 \\ & ~~\text{ in millions }\\ PRIVATE & \text{ 2004 Private expenditure} & 1 & 2.52 & 2.40 & 1.33 & 0.30 & 8.50 \\ ~~HEALTH& ~~\text{on health, % of GDP} \\ PUBLIC & \text{ Public expenditure} & 28 & 4.69 & 4.60 & 2.05 & 0.60 & 13.40 \\ ~~EDUCATION& ~~ \text{ on education, % of GDP} \\ RESEAR & \text{ Researchers in R & D,} & 95 & 2,034.66 & 848.00 & 4,942.93 & 15.00 & 45,454.00 \\ ~~CHERS&~~ \text{ per million people} & \\ SMOKING & \text{ Prevalence of smoking,} & 88 & 35.09 & 32.00 & 14.40 & 6.00 & 68.00 \\ & ~~\text{ (male) % of adults } \\ \hline LIFEEXP & \text{ Life expectancy at birth,}& & 67.05 & 71.00 & 11.08 & 40.50 & 82.30 \\ & ~~ \text{ in years } \\ \hline \end{array} } \]

1.9 Suplemento Técnico - Teorema del Límite Central

Los teoremas del límite central forman la base para gran parte de la inferencia estadística utilizada en el análisis de regresión. Por lo tanto, es útil proporcionar una declaración explícita de una versión del teorema del límite central.

Teorema del Límite Central. Supongamos que \(y_1, \ldots, y_n\) están distribuidos de manera independiente con media \(\mu\), varianza finita \(\sigma^2\) y \(\mathrm{E}|y|^3\) es finito. Entonces, \[ \lim_{n \rightarrow \infty} \Pr \left( \frac{\sqrt{n}}{\sigma }(\overline{y} - \mu ) \leq x \right) = \Phi \left( x \right), \] para cada \(x\), donde \(\Phi \left( \cdot \right)\) es la función de distribución normal estándar.

Bajo las suposiciones de este teorema, la distribución reescalada de \(\overline{y}\) se aproxima a una distribución normal estándar a medida que aumenta el tamaño de la muestra, \(n\). Interpretamos esto como que, para tamaños de muestra ‘grandes’, la distribución de \(\overline{y}\) puede aproximarse mediante una distribución normal. Investigaciones empíricas han mostrado que tamaños de muestra de \(n = 25\) a 50 proporcionan aproximaciones adecuadas para la mayoría de los propósitos.

¿Cuándo no funciona bien el teorema del límite central? Algunos conocimientos se proporcionan mediante otro resultado de la estadística matemática.

Aproximación de Edgeworth. Supongamos que \(y_1, \ldots, y_n\) están distribuidos idéntica e independientemente con media \(\mu\), varianza finita \(\sigma^2\) y \(\mathrm{E}|y|^3\) es finito. Entonces, \[ \Pr \left( \frac{\sqrt{n}}{\sigma }(\overline{y} - \mu ) \leq x \right) = \Phi \left( x \right) + \frac{1}{6}\frac{1}{\sqrt{2\pi }} e^{-x^2/2} \frac{\mathrm{E}(y - \mu)^3}{\sigma^3 \sqrt{n}} + \frac{h_n}{\sqrt{n}}, \] para cada \(x\), donde \(h_n \rightarrow 0\) a medida que \(n \rightarrow \infty\).

Este resultado sugiere que la distribución de \(\bar{y}\) se acerca más a una distribución normal a medida que la asimetría, \(\mathrm{E}(\overline{y} - \mu)^3\), se acerca a cero. Esto es importante en aplicaciones de seguros porque muchas distribuciones tienden a ser asimétricas. Históricamente, los analistas utilizaban el segundo término en el lado derecho del resultado para proporcionar una ‘corrección’ para la aproximación de la curva normal. Véase, por ejemplo, Beard, Pentikäinen y Pesonen (1984) para una discusión adicional sobre las aproximaciones de Edgeworth en la ciencia actuarial. Una alternativa (utilizada en este libro) que vimos en la Sección 1.3 es transformar los datos, logrando así una aproximada simetría. Como sugiere el teorema de aproximación de Edgeworth, si nuestra población parental es cercana a simétrica, entonces la distribución de \(\overline{y}\) será aproximadamente normal.